2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
大口径地平式太阳望远镜是当今太阳地基观测仪器的一个发展方向[1],为实现太阳高时空分辨率观测,大口径太阳望远镜对指向跟踪精度的要求越来越高。指向精度是指望远镜光轴对准观测目标的精确程度[2],跟踪精度是指望远镜长时间跟踪观测目标的精确程度。高精度指向跟踪能使太阳望远镜精确指向日面的某一微小观测目标并使目标长时间稳定在视场中,实现高精度、长时间成像或光谱等观测。例如,1 m新真空太阳望远镜的指向精度要求5″,国家天文台用于太阳磁场精确测量的中红外观测系统(Accurate Infrared Magnetic field measurements of the Sun, AIMS)的指向精度要求10″,美国的DKIST(Daniel Ken Inouye Solar Telescope, DKIST)的指向精度要求5″,这些望远镜的开环跟踪精度都要求达到30 min内1~2″。
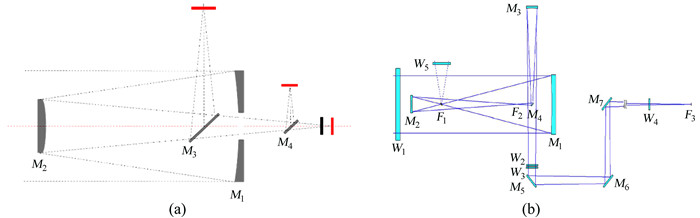
太阳望远镜的科学仪器比较特殊,对系统稳定性要求非常高,通常固定安装在库德焦面,不像夜天文望远镜安装在卡焦并随望远镜转动。因而太阳望远镜主副镜系统后端需要比较复杂的引导光路,并使主光轴穿过高度轴、方位轴和消旋轴,最后延伸到不随望远镜转动的库德焦点。图 1(a)为丽江2.4 m望远镜系统,终端仪器工作在卡焦位置,光路相对简单[2]。图 1(b)为抚仙湖的1 m新真空太阳望远镜,光学系统的格里高利焦点(卡焦)到库德焦面有复杂的引导光路[3]。
|
| 图 1 夜天文望远镜与太阳望远镜光机结构比较。(a)丽江2.4 m望远镜光学结构;(b)1 m新真空太阳望远镜光学结构 Fig. 1 Comparison of optical and mechanical structures between night telescope and solar telescope (a) Optical structure of Lijiang 2.4 m telescope; (b) optical structure of NVST |
地平式太阳望远镜指向跟踪过程中,光学系统需要随望远镜高度轴、方位轴和消旋轴运动。以1 m新真空太阳望远镜为例,M1, M2, M3, M4, M5, M6, M7与望远镜的方位同步运动;M1, M2和M4位置相对固定,但与望远镜高度轴同步运动;为了对目标进行消旋,光路还要随消旋轴运动[4]。由于光机制造和装调误差必然存在,望远镜主光轴、高度轴、方位轴和消旋轴不可能完全重合,导致即使格里高利焦点的像保持静止,库德焦面的像还有非常复杂的运动,这就是库德焦面的二次跟踪误差,是地平式太阳望远镜库德焦面实现高精度指向跟踪面临的难题。对于离轴格里高利系统的AIMS太阳望远镜,库德焦面的图像运动更加复杂。
指向模型是提高天文望远镜指向精度和开环跟踪精度的一种控制策略,其过程是先通过均匀密集采集全天区已知位置的星的指向误差建立模型,然后用模型实时预测望远镜需要修正的误差,进而提高望远镜的指向跟踪精度。夜天文望远镜的指向模型已经发展得比较成熟,应用最广的是TPOINT和STARCAL等指向模型。但将这些模型应用到地平式太阳望远镜库德焦面时,无法得到理想的指向精度和开环跟踪精度。究其原因,这些模型都是基于望远镜卡焦的物理机制建立的,比如望远镜方位轴不铅垂、高度轴不水平、主副镜光轴弯沉等误差描述项。但这些模型对于卡焦之后的库德光路中的旋转轴不同心等误差没有相关描述项,因为这些误差项与主光轴、高度轴、方位轴和消旋轴的同心度有很大关系,与每台太阳望远镜的穿轴误差密切相关,需要事先知道这些轴在库德焦面的旋转中心位置才能在模型中建立相应的误差描述项。
1 库德焦面跟踪误差仿真分析地平式太阳望远镜库德焦面复杂的二次跟踪误差是由于主光轴、高度轴、方位轴和消旋轴不可能完全重合引入的。望远镜跟踪过程中,库德焦面的图像是旋转的,为了消除图像旋转,消旋系统需要反方向运动来抵消图像旋转。在地平式太阳望远镜的库德焦面上,图像旋转由3个分量组成,它们分别是围绕主副镜系统主光轴的旋转分量,这个分量是由于赤道坐标系与地平坐标系之间的转换产生的;另外还有围绕高度轴的旋转分量和围绕方位轴的旋转分量,是由于地平式望远镜跟踪运动引起的,库德光路需要围绕望远镜高度轴和方位轴旋转,这3个分量的旋转角用公式表示为[5]
| $ \begin{array}{l} \theta = {\mathop{\rm acos}\nolimits} \left( {\frac{{\sin \phi - \sin E\sin \delta }}{{\cos E\cos \delta }}} \right), \\ E = {\mathop{\rm asin}\nolimits} (\sin \phi \sin \delta + \cos \phi \cos \delta \cos H), \\ A = {\mathop{\rm acos}\nolimits} \left( {\frac{{\sin \delta - \sin E}}{{\cos E\cos \phi }}} \right), \end{array} $ | (1) |
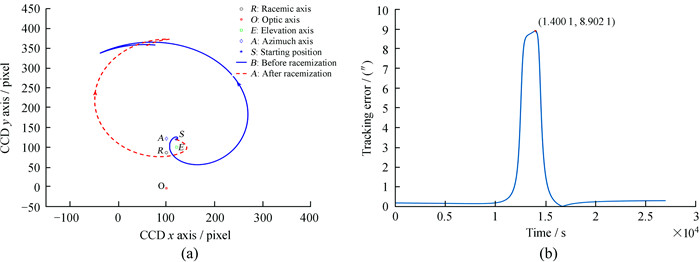
其中,θ为地平坐标系下的物方视场旋转角;E为高度角;A为方位角,此处A和E都为像方视场旋转角分量;ϕ为地理纬度;δ为目标赤经;H为时角。由于这3个分量在库德焦面的旋转中心位置及其关系是由望远镜的光机制造误差和装调误差决定的,除了消旋轴中心能方便实测之外,光轴无法实测,高度轴和方位轴也难以实测。为了分析地平式太阳望远镜库德焦面复杂的跟踪误差,参考库德光路中各反射镜的装调公差[6],假设这3个旋转中心在CCD上的位置如图 2(a),CCD上一个像素对应0.3″。我们以1 m新真空太阳望远镜为例,分析在夏至日过中天半小时内望远镜在库德焦面产生的二次跟踪误差。
|
| 图 2 库德焦面二次跟踪误差示意图。(a)3个旋转分量中心及消旋前后运动轨迹;(b)30 min跟踪误差随时间的变化 Fig. 2 Schematic diagram of the Coude focal plane secondary tracking error. (a) The center of three rotation components and the track before and after racemization; (b) variation of 30 minutes tracking error with time |
从图 2(a)中消旋前后的运动轨迹对比可知,消旋系统虽然将库德焦面的图像旋转消除了,但是由于几个旋转轴的中心不同,导致消旋后图像不能回到原来的位置,产生了另外的图像移动,这就是二次跟踪误差。图 2(b)选取夏至日太阳过中天30 min分析指向跟踪误差,最大达到8.90″。如果光机装调误差较大,各轴系的旋转中心在库德焦面更加分散,跟踪误差更大。
根据仿真分析可知,地平式太阳望远镜库德焦面上的二次跟踪误差十分复杂,要从物理机制上完成建模,必须事先准确测量光轴、方位轴、高度轴和消旋轴在库德焦面的具体位置,这是极其困难的工作。本文利用基于机器学习的实测建模方法解决这个问题。
2 基于机器学习的库德焦面指向跟踪误差建模 2.1 概述机器学习可以在模型未知的情况下,通过算法对实测指向误差数据进行归纳和抽象,生成指向跟踪误差模型,通过模型实时预测观测目标对应的望远镜方位坐标和高度坐标,实现望远镜高精度的指向跟踪。在库德焦面实测指向误差时,控制系统记录待测星的地平坐标方位AS、高度ES,以及星在焦面探测器(CCD)中心位置时望远镜的地平坐标方位AT、高度ET。理想情况下,AS与AT相等,ES与ET相等,实际情况由于存在指向误差,它们是不相等的。AT是AS与ES的函数fA(AS, ES),ET也是AS与ES的函数fE(AS, ES),可以理解为两个误差曲面拟合,这是一个典型的回归问题。
机器学习中常用的回归算法有支持向量回归(Support Vector Regression, SVR)、逻辑回归、广义局部线性模型、多项式回归等[7]。一般回归算法需要大量的训练集,也就是要事先获得大量的实测指向误差,这使得实际观测工作量非常大,难以实现。所以本文采用能处理小样本数据的支持向量回归建模,这个算法还具有较强的泛化能力[8]。
2.2 支持向量回归的原理本文采用文[8-9]的方法,支持向量回归可以简化描述为把样本集作为S={xi, yi}i=1n,其中x为输入向量,xi∈Rn;y为相应的输出向量,yi∈Rn。这个算法利用非线性映射将样本集从低维空间映射到高维空间,最终拟合训练集样本。该映射定义为[9]
| $ f(x)=\omega \phi(x)+b, $ | (2) |
其中,x为输入数据;ϕ(x)为非线性映射函数;ω为权重;b为截距。根据结构风险最小化原则,f(x)等效于求解优化问题[9],即
| $ f(x)=\frac{1}{2} \omega^2+C \sum\limits_i^n L\left[f\left(x_i\right), y_i\right] \text {, } $ | (3) |
其中,L为损失函数;C为惩罚因子。加入松弛变量{ξi}i=1n和{ξi*}i=1n纠正不规则的因子,可以得到[9]
| $ \min R(\omega, b, \xi)=\frac{1}{2} \omega^2+C \sum\limits_i^n\left(\xi_i+\zeta_i^*\right), $ | (4) |
| $ \mathit{s}.t.\left\{ {\begin{array}{*{20}{c}} {{y_i} - \omega \phi (x) - b \le \varepsilon + {\xi _i}}\\ {\omega \phi (x) + b \le \varepsilon + \xi _i^*}\\ {{\xi _i}, \xi _i^* \ge 0} \end{array}} \right., $ | (5) |
其中,ε为不敏感损失因子(允许的最大误差),ε>0。将回归问题转换为求解目标函数的最小化问题,利用对偶原理,同时引入拉格朗日乘法算子,可以转换为[9]
| $ \max R\left(\alpha_i^*, \alpha_i\right)=-\frac{1}{2} \sum\limits_{i, j}^n\left(\alpha_i^*-\alpha_i\right)\left(\alpha_j^*-\alpha_j\right) \phi\left(x_i\right) \phi\left(x_j\right)-\sum\limits_i^n \alpha_i\left(y_i-\varepsilon\right)+\sum\limits_i^n \alpha_i^*\left(y_j-\varepsilon\right), $ | (6) |
| $ \mathit{s}{\rm{. }}\mathit{t}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {\left( {\alpha _i^* - {\alpha _i}} \right)} = 0}\\ {0 \le {\alpha _i}, \alpha _i^* \le C} \end{array}} \right., $ | (7) |
其中,αi和αi*为拉格朗日乘数。引入Mercer定理,上述表达式变换为[9]
| $ f(x) = w\phi (x) + b = \sum\limits_{i = 1}^n {\left( {\alpha _i^* - {\alpha _i}} \right)} K\left( {{x_i}, x} \right), $ | (8) |
其中,K(xi, x)=ϕ(xi)ϕ(xj)为核函数;0≤ai,ai*≤C。考虑到实测数据误差分布及模型实际应用,本文选取多项式核函数,定义为
| $ K_{\text {poly }}\left(x_i, x\right)=\left(x x_i+1\right)^d, $ | (9) |
其中,d表示多项式的阶数,d越大,多项式越复杂,计算量越大。在实际的指向误差建模过程中,自变量可以表示为(x1, x2)=(A, E)。
惩罚因子C表示对模型复杂度与误差精度之间的折中,C越大,模型泛化能力越差,C越小,模型的训练误差越大,ε表示样本之间的区分程度,这两个参数直接决定了支持向量回归的准确性。由于原始数据中指向误差是关于高度值和方位值的函数,比较简单直观,再结合实际的模型训练效果,本文中C设置为500,ε设置为0.01。
3 实测与建模 3.1 指向误差实测在指向误差实测过程中,采用表 1的格式进行数据记录。AT和ET的具体测量过程为给望远镜控制系统输入某一颗较亮恒星的理论地平坐标(AS,ES),然后控制望远镜指向该星并处于跟踪状态,通过库德焦面成像探测器实时采集星像并给出星像的重心。理想情况下,星像重心位置应该在CCD的中心(认为是视场中心),但是由于望远镜存在系统误差,星像重心位置并不在CCD的中心,微调望远镜,使星像重心位置处在CCD中心。这时记录望远镜的(AT,ET),它与(AS,ES)之间的差值就是该星的指向误差。AS的取值范围为0~360°,正北方向为0°,顺时针取值;ES的取值范围为0~90°,当望远镜光轴指向天顶时,ES为90°。
| Number | AT | ET | AS | ES |
| 1 | 149.745 463 | 42.520 237 | 149.700 3 | 42.523 03 |
| 2 | 170.781 463 | 61.170 897 | 170.786 62 | 61.158 965 |
| …… | …… | …… | …… | …… |
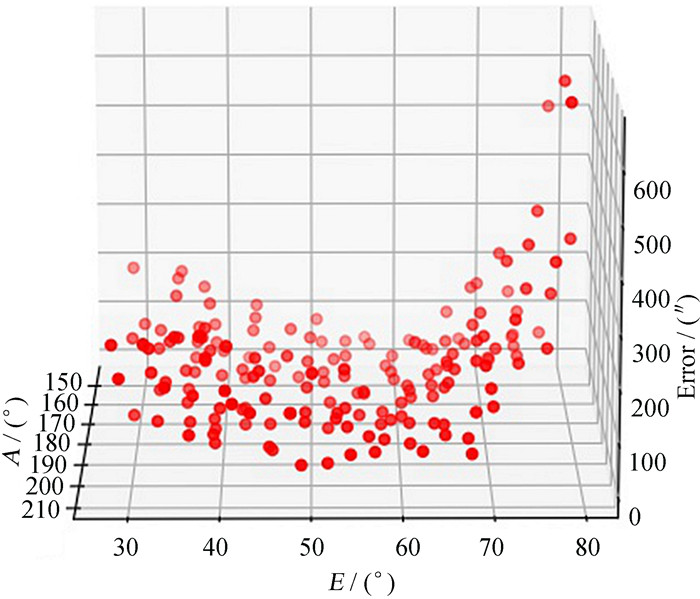
实测工作在1 m新真空太阳望远镜上进行,成像选取TiO通道,CCD像元比是0.04,由于受望远镜工作范围的影响,实测数据只能在一部分天区进行。观测时间是2021年1月14日晚,共测得138颗星的指向误差。图 3是实测数据指向误差分布,最大误差为650.55″,均方根为115.88″。
|
| 图 3 数据的误差分布 Fig. 3 Error distribution of data |
模型评价指标采用均方根,均方根越小,表示模型的预测效果越好。在地平坐标系下,误差公式为
| $ \begin{array}{l} \mathit{Error} = \sqrt {{{\left[ {\Delta A\cos {E_{\rm{S}}}} \right]}^2} + \Delta {E^2}} , \\ \;\;\Delta A = {A_{\rm{S}}} - {A_{\rm{T}}}, \Delta E = {E_{\rm{S}}} - {E_{\rm{T}}}, \end{array} $ | (10) |
| $ R M S=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(\left[\Delta A_i \cos E_{\mathrm{S}}^i\right]^2+\Delta E_i^2\right)} . $ | (11) |
为了在建模时有不同的测试集和训练集,以及测试建模方法对数据是否敏感,将实测的138颗星的误差数据抽样为6份,抽样方法是将星的位置尽量均匀分布在138颗星所在天区。误差数据抽样为6份后,每份有23颗星的指向误差数据,分别标记为train000, train001, train002, train003, train004, train005。第1次建模时,把train000, train001, train002, train003, train004合并为训练集(即建模数据有115个),train005为测试集(23个数据)。第2次建模时,把train001, train002, train003, train004, train005合并为训练集,第train000组为测试集。如此不断变换测试集和训练集的数据,最后对比6次测试集的统计结果,看是否有大的差别。
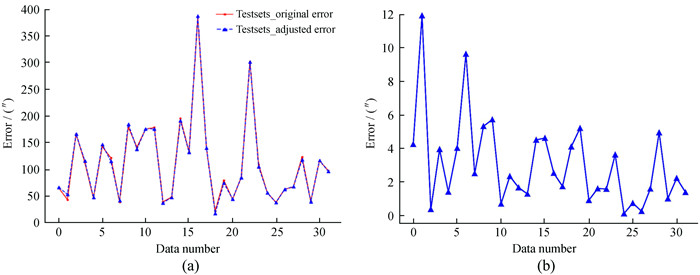
实验1结果如图 4,图 4(a)是测试集的预测值和原始值的拟合程度,拟合结果比较好。图 4(b)是测试集中预测值和实际值之间的误差,在图中测试集的预测误差最大为12.89″,均方根为2.89″,说明训练模型对测试集的预测效果比较好。
|
| 图 4 测试集的预测误差分布。(a)预测值和实际值的拟合情况;(b)预测值和实际值的误差分布 Fig. 4 Error distribution of prediction of test sets. (a) Fitting of predicted value and actual value; (b) error distribution of predicted value and actual value |
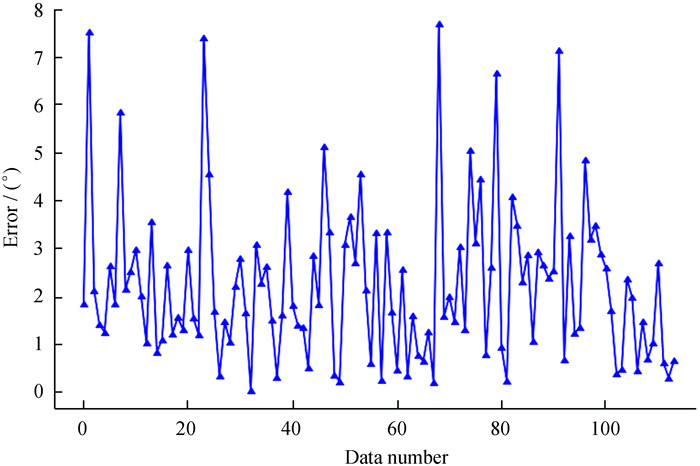
利用支持向量回归模型对训练集做反向预测,得到的结果如图 5。训练集的预测均方根为2.84″,预测误差最大为8.92″。通过对比训练集和测试集的预测误差发现,两者的误差相差不大。
|
| 图 5 训练集的预测误差分布 Fig. 5 Error distribution of prediction of training set |
之后我们采用不同的训练集和测试集进行了6次实验,得到的结果如表 2。从表 2可以看出,测试集的均方根在3″左右,说明使用支持向量回归方法构建的指向模型有效。
| Number of experiments | Test set | Error RMS/(″) | Maximum error/(″) |
| 1 | train000 | 2.89 | 12.89 |
| 2 | train001 | 3.29 | 13.43 |
| 3 | train002 | 3.59 | 12.15 |
| 4 | train003 | 3.34 | 11.27 |
| 5 | train004 | 3.28 | 11.06 |
| 6 | train005 | 3.06 | 11.94 |
为了验证模型在望远镜实际观测中的效果,将模型加载到控制系统,并在1 m新真空太阳望远镜上进行指向误差实测和跟踪误差实测。
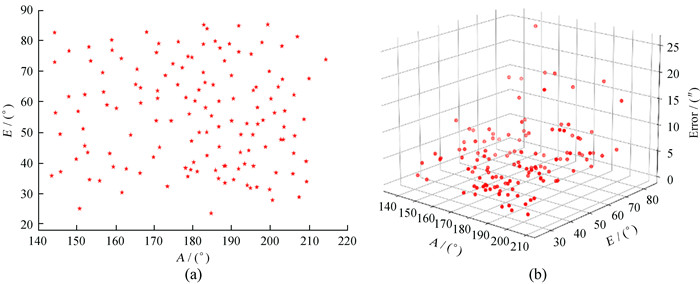
指向误差实测星为138颗,图 6(a)是138颗星在天区的分布。图 6(b)为数据建模后的实测误差,误差最大为25.02″,均方根为3.98″。
|
| 图 6 指向精度实测效果的分析。(a)138颗星的在天区的分布;(b)实测误差的分布 Fig. 6 Measurement of pointing accuracy. (a) The distribution of 138 stars in the sky; (b) distribution of measured error |
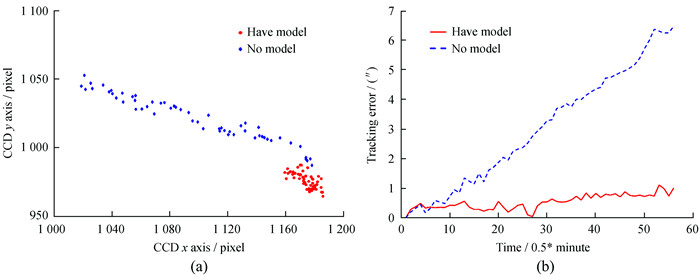
实测跟踪误差在1 m新真空太阳望远镜上,2022年1月22日晚选取某一恒星做长时间跟踪观测,加模型和不加模型的跟踪时长各为30 min,实验结果如图 7。图 7(a)是星像在探测器上的运动轨迹,圆点表示加了模型的星的运动轨迹,方块表示没加模型的星的运动轨迹,图 7(b)是望远镜30 min内的跟踪误差统计。由图 7可知,模型修正前跟踪误差为6.46″,模型修正后跟踪误差为1.10″。
|
| 图 7 跟踪误差实测结果。(a)星像的运动轨迹;(b)跟踪误差统计 Fig. 7 Measured results of tracking error. (a) Star image trajectory; (b) tacking error statistics |
地平式太阳望远镜主光轴、高度轴、方位轴和消旋轴的同心度是影响库德焦面跟踪误差的主要因素之一,由于难以实测这些轴在库德焦面的具体位置,所以夜天文望远镜上常用的TPOINT等软件无法对这类误差进行建模。为了提高地平式太阳望远镜库德焦面的指向跟踪精度,本文提出了一种基于支持向量回归算法构建库德焦面指向跟踪模型的新方法,并在1 m新真空太阳望远镜上进行了实测建模。实测结果表明,新模型可以有效校正库德焦面的指向跟踪误差。在模型改正之前,1 m新真空太阳望远镜在库德焦面的指向误差均方根为115.88″,30 min跟踪误差为6.46″。经过模型改正后,望远镜在库德焦面的指向误差均方根为3.98″,30 min跟踪误差为1.10″。由此可见,基于机器学习的支持向量回归建模方法能有效提高地平式太阳望远镜库德焦面的指向跟踪精度。
| [1] |
刘忠, 邓元勇, 杨德华, 等. 中国巨型太阳望远镜[J]. 中国科学: 物理学力学天文学, 2019, 49(5): 059604 LIU Z, DENG Y Y, YANG D H, et al. Chinese Giant Solar Telescope[J]. Scientia Sinica: Physica, Mechanica&Astronomica, 2019, 49(5): 059604. |
| [2] |
王欣, 潘君骅. 2.4 m天文望远镜光学系统的设计及副镜检验的几种可能方案[J]. 云南天文台台刊, 2002(2): 41–49 WANG X, PAN J H. Optic system design of a 2.4 m class telescope and several methods for testing the secondary mirror[J]. Publications of the Yunnan Observatory, 2002(2): 41–49. |
| [3] | LIU Z, XU J, GU B Z, et al. New vacuum solar telescope and observations with high resolution[J]. Research in Astronomy and Astrophysics, 2014, 14(6): 705–718. DOI: 10.1088/1674-4527/14/6/009 |
| [4] |
陈宇超, 柳光乾. NVST的长期跟踪误差分析及改正[J]. 天文研究与技术, 2016, 13(2): 205–212 CHEN Y C, LIU G Q. The error analysis and correction of NVST's long-term tracking[J]. Astronomical Research&Technology, 2016, 13(2): 205–212. DOI: 10.3969/j.issn.1672-7673.2016.02.010 |
| [5] |
柳光乾, 付玉, 程向明. 1米太阳望远镜光谱仪像旋转及消旋控制[J]. 天文研究与技术, 2012, 9(1): 96–92 LIU G Q, FU Y, CHENG X M. Image-field rotation and control of counter rotation for the spectrograph of the 1 m solar telescopeof the Yunnan Observatory[J]. Astronomical Research&Technology, 2012, 9(1): 96–92. |
| [6] |
张丽敏, 明名, 杨飞, 等. 大口径望远镜Coude光路光机结构设计研究[J]. 光电工程, 2011, 38(5): 64–68 ZHANG L M, MING M, YANG F, et al. Design for Coude optic-mechanical structure of large aperture telescope[J]. Opto-Electronic Engineering, 2011, 38(5): 64–68. |
| [7] |
刘辉, 季凯帆, 金振宇. 机器学习在太阳物理中的应用[J]. 中国科学: 物理学力学天文学, 2019, 49(10): 109601 LIU H, JI K F, JIN Z Y. The application of machine learning in solar physics[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2019, 49(10): 109601. |
| [8] | CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273–297. |
| [9] |
徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 1995, 20(3): 3693–3704 XU J N, NI Y L, ZHU C B. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transaction of China Electrotechnical Society, 1995, 20(3): 3693–3704. |



