2. 中国科学院大学, 北京 100049;
3. 国家基础学科公共科学数据中心, 北京 100190;
4. 中国科学院射电天文重点实验室, 江苏 南京 210033;
5. 上海市导航定位重点实验室, 上海 200030
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. National Basic Public Science Data Center, Beijing 100190, China;
4. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
5. Shanghai Key Laboratory of Navigation and Positioning, Shanghai 200030, China
甚长基线干涉测量是一种具有高分辨率、高精度特点的射电干涉技术[1]。它采用原子钟控制的高稳定独立本振系统和数据采集装置,通过多个望远镜同时接收目标源信号,记录数据并发送到异地的数据处理中心,经处理得到观测结果。在甚长基线干涉测量观测中,两台射电望远镜间的距离称为基线,它决定甚长基线干涉测量的最大分辨率[2]。若有空间望远镜与地面望远镜构成空地甚长基线干涉测量系统,基线长度超过地球直径,可实现更高的分辨率。我国探月工程四期任务将利用嫦娥七号中继星上的4.1 m口径抛物面天线,进行月地空间甚长基线干涉测量试验。不同于常规地基甚长基线干涉测量[3],受中继星轨道扰动和设备时延的影响,射电源预报时延模型可能和实际时延有较大差异,无法引导相关处理机正常工作。通过射电源条纹搜索,可确定实际相关处理机所需的高精度时延模型,用于空间甚长基线干涉测量空地基线相关处理。
目前,在探月工程中,探测器信号相关处理时,采用差分单向测距(Differential One-way Ranging, DOR)信号的点频信号特征设计条纹搜索算法[4]。而射电源信号是白噪声信号,无法利用现有的探测器信号搜索算法。针对射电源信号的条纹搜索有eFFT条纹搜索算法、CAF-W条纹搜索算法[5]和多重网格条纹搜索算法[6]。eFFT条纹搜索算法和CAF-W条纹搜索算法可以实现残余时延和时延率的计算,但主要用于强源的时延模型搜索。多重网格条纹搜索算法的基本思想是建立多层次、不同尺寸的网格,通过这些网格,在不同范围内搜索需要的目标。多重网格条纹搜索算法使用线性时延模型进行相关处理,在时延-时延率平面内搜索条纹,适用于信号较强、短时间积分就能得到条纹的应用场景。由于空间小口径天线接收信号较弱,获得干涉条纹需要进行较长积分时间,使用通常的线性时延模型无法保证较长时间范围内的相关处理机模型时延精度,需构造精度更高的二次项时延模型。如果在常规多重网格中增加时延二次项,会使搜索空间从二维扩展到三维,计算复杂度增加一个量级。
本文基于多重网格条纹搜索算法,提出了一种用于空间甚长基线干涉测量的射电源条纹搜索算法:首先建立关于时延和时延率的二维搜索网格,使用每个网格点对应的先验时延和时延率信息构建线性时延模型,对原始数据分时段相关处理;然后由二维傅里叶变换求解残余时延和时延率后进行补偿,得到每个时段的时延和时延率,计算每个网格点对应的相关幅度值;最后在最大相关幅度值对应的网格点上重构二次项时延模型。采用该算法,对俄罗斯RadioAstron空间甚长基线干涉测量的实际观测数据进行相关处理时取得了较好的效果。
1 射电源条纹搜索算法目前,中国甚长基线干涉测量网相关机使用五次项时延模型进行相关处理。在条纹搜索过程中,为减少计算复杂度,通常使用由时延常数项和时延一次项系数构成的线性时延模型。但随着时间范围的扩大,线性时延模型的误差与五次多项式模型的误差也会增加。综合考虑条纹搜索计算量与模型精度因素,我们构建由常数项、一次项系数和二次项系数构成的二次项时延模型。
1.1 相关处理算法假设两台站接收的目标源射频信号分别为s1(t)和s2(t),同一波前信号到达两台站时延差为τ,则
| $ s_2(t)=s_1(t+\tau) . $ | (1) |
由射频信号得到的基频信号
| $ x_1(t)=s_1(t) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 t}, $ | (2) |
| $ x_2(t)=s_2(t) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 t}=s_1(t+\tau) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 t}, $ | (3) |
其中,f0为通道的天空频率。相关处理以台站1为参考,使用预报模型τc对台站2进行时延补偿,即
| $ x_2\left(t-\tau_{\mathrm{c}}\right)=s_2\left(t-\tau_{\mathrm{c}}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f_0\left(t-\tau_{\mathrm{c}}\right)}=s_1\left(t+\tau-\tau_{\mathrm{c}}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f_0\left(t-\tau_{\mathrm{c}}\right)}, $ | (4) |
经过条纹旋转后,
| $ x_2\left(t-\tau_{\mathrm{c}}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 \tau_{\mathrm{c}}}=s_2\left(t-\tau_{\mathrm{c}}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 t}=s_1\left(t+\tau-\tau_{\mathrm{c}}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 t}. $ | (5) |
对台站1和台站2的信号进行傅里叶变换,
| $ \begin{gathered} x_1(t) \stackrel{\mathrm{FFT}}{\Rightarrow} S_1\left(f+f_0\right), \\ x_2\left(t-\tau_{\mathrm{c}}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f_0 \tau_{\mathrm{c}}} \stackrel{\mathrm{FFT}}{\Rightarrow} S_2\left(f+f_0\right) \mathrm{e}^{-\mathrm{j} 2 \pi\left(f+f_0\right) \tau_{\mathrm{c}}}=S_1\left(f+f_0\right) \mathrm{e}^{-\mathrm{j} 2 \pi\left(f+f_0\right)\left(\tau_{\mathrm{c}}-\tau\right)} . \end{gathered} $ | (6) |
S1(f+f0)为台站1信号经过频率转换后的功率谱,共轭相乘得到两台站的互相关功率谱为
| $ P_{12}(f)=\left|S_1\left(f+f_0\right)\right|^2 \mathrm{e}^{-\mathrm{j} 2 \pi\left(f+f_0\right)\left(\tau_e-\tau\right)} . $ | (7) |
由(7)式可知,当残余时延τc-τ达到最小值时,两台站的互相关功率谱达到最大峰值。
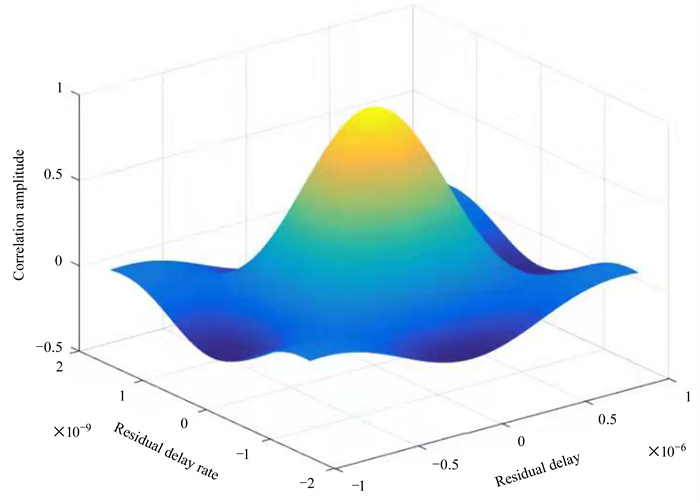
1.2 残余时延搜索算法根据二维傅里叶变换的性质可知,相关处理得到的互相关谱二维傅里叶变换后,可以得到一个关于残余时延和时延率的二维互相关函数[7],如图 1,其公式为
| $ F(\Delta \tau, \Delta \dot{\tau})=\left|\int_0^B\left\{\int_0^T P_{12}(f, t) \mathrm{e}^{-\mathrm{i} 2 \pi f_0 \Delta \dot\tau t} \mathrm{~d} t\right\} \mathrm{e}^{-\mathrm{i} 2 \pi \Delta \dot\tau f} \mathrm{~d} f\right|, $ | (8) |
|
| 图 1 二维傅里叶变换残余时延搜索图 Fig. 1 Residual delay search of 2-D Fourier transform |
其中,Δτ为残余时延;
| $ F\left(a_{\mathrm{r}}, \quad b_{\mathrm{r}}\right)=\left|\frac{2 B T}{N M} \sum\limits_{n=0}^{N-1}\left\{\sum\limits_{m=0}^{M-1} P_{12}(n, m) \mathrm{e}^{-\mathrm{i} 2 \pi f_0 b_{\mathrm{r}} m T / M}\right\} \mathrm{e}^{-\mathrm{i} 4 \pi a_{\mathrm{r}} n B / N}\right|, $ | (9) |
其中,F(ar, br)为经过二维傅里叶变换后得到的相关幅度值[8];ar和br分别为离散化后的残余时延和时延率;N为频域的傅里叶变换点数;M为时域的傅里叶变换点数。
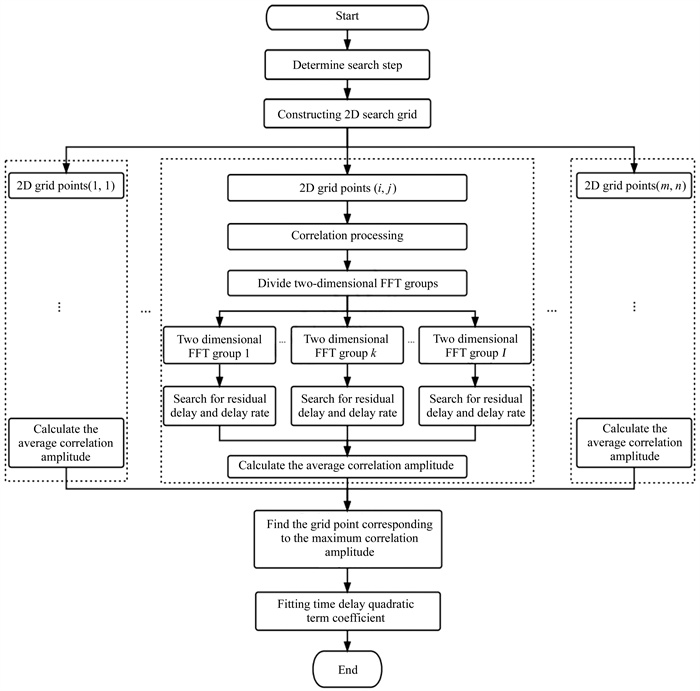
1.3 条纹搜索与二次项时延模型重构流程根据以上原理,对于空间甚长基线干涉测量射电源条纹搜索与二次项时延模型重构流程如图 2。由二维傅里叶变换的性质可知,相关后二维傅里叶变换的残余时延和时延率的范围分别为
| $ d_{\text {step }}=\frac{N}{10 B}, $ | (10) |
|
| 图 2 射电源条纹搜索与二次项时延模型重构流程图 Fig. 2 Flow chart of radio source fringe search and quadratic term delay model reconstruction |
时延率步长为
| $ d r_{\text {step }}=\frac{M}{2 f_0 T}. $ | (11) |
条纹搜索的步长与时延模型精度和计算量密切相关,如果搜索步长设置过大,得到的模型精度太低,无法用于后续数据处理;如果步长设置太小,由于目前的算法采用全网格搜索策略,依次计算每个网格点数据会极大影响整体的计算效率。我们注意到步长设置较小时可能有多组网格点搜索到满足精度要求的模型,后续会研究基于二维随机游走的网格搜索策略,找到合适的时延模型就停止计算,这样可以有效提高效率。
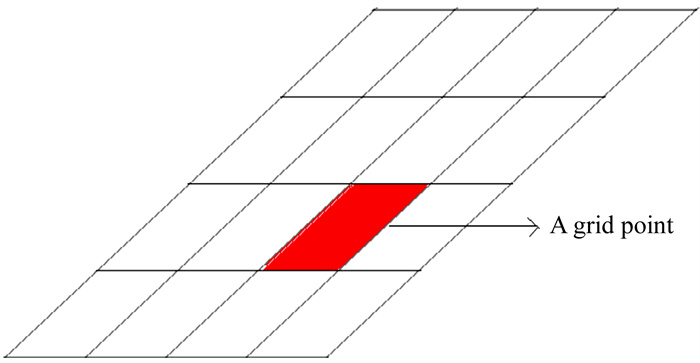
确定步长后,根据搜索范围和先验时延模型划分网格点。每个网格点对应不同的时延和时延率,代表经过不同时延补偿的数据处理。如图 3,以先验时延模型中的时延和时延率为中心点,等步长计算每个网格点对应的时延和时延率。
|
| 图 3 二维网格示意图 Fig. 3 Schematic diagram of two-dimensional grids |
由于弱信号使用线性时延模型进行长时间积分无法保证时延精度,获得干涉条纹,所以将原始数据划为I组较短的数据段进行处理,每一组为一个二维傅里叶变换组,时间长度为T。在每个网格点上构造线性时延对原始数据补偿后进行相关处理,相关处理的积分时间为T/M,一个二维傅里叶变换组的数据大小为MN。得到两台站的互相关功率谱后,利用(9)式对每一组的相关谱进行二维傅里叶变换,得到每个网格点上的I组残余时延、时延率和相关幅度值,利用最大相关幅度的平均值确定最优解对应的网格点,在该网格点上进行时延和时延率的拟合,得到最优的二次项时延系数。
在拟合时,将每一组的残余时延air和时延率bir,与相关处理预报时延模型中的初始时延aic和时延率bic相加,可以得到该组的时延ai和时延率bi,即
| $ a_i=a_i^{\mathrm{c}}+a_i^{\mathrm{r}}, $ | (12) |
| $ b_i=b_i^{\mathrm{c}}+b_i^{\mathrm{r}} \text {. } $ | (13) |
甚长基线干涉测量观测具有时间连续性,时延模型也应该是连续的。但在求解残余时延的过程中,数据分段导致每一组之间的时延具有间断点,在拟合二次项时延系数时,需要根据连续的约束条件,即保持第1组的时延a0不变,修正其余组的时延ai,使之与前一组末的时延相等,即
| $ \left\{\begin{array}{c} a_0^{\mathrm{m}}=a_0 \\ a_i^{\mathrm{m}}=a_{i-1}+b_{i-1} T \end{array}, 0<i<I, \right. $ | (14) |
其中,aim为改正后的时延;I为二维傅里叶变换组的个数。
经过上述时延改正后,再进行二次项时延系数拟合。设未知的二次项时延系数为[x0x1x2],求解时延的多项式为
| $ a_i^{\mathrm{m}}=x_0+x_1 t_i+x_2 t_i^2, $ | (15) |
其中,ti=iT为每个二维傅里叶变换组开始的时间。对(15)式右端求导,得到时延率的多项式为
| $ b_i=x_1+2 x_2 t_i \text {. } $ | (16) |
联立(15)式和(16)式建立超定方程组,再利用正交三角分解法求解[9]。
2 算法验证RadioAstron项目是前苏联在20世纪80年代中期提出的一项空间甚长基线干涉测量计划。2011年,俄罗斯发射了10 m口径的RadioAstron空间射电望远镜(Spektr-R, Ra)卫星。Ra与地面多个大型射电望远镜构成空间甚长基线干涉测量系统,接收频段为0.3 GHz,1.6 GHz,5.0 GHz和22 GHz,轨道高度近地点600 km,远地点330 000 km,通过联合地面望远镜进行干涉测量。
为验证空间甚长基线干涉测量射电源条纹搜索算法,我们使用2014年空间射电望远镜Ra与美国阿雷西博射电望远镜(Arecibo Radio Telescope, Ar)联合观测射电源0823+033的数据进行干涉处理。观测起始时间为2014年4月11日23时07分00秒,结束时间为2014年4月11日23时07分59秒。其中,Ar站为2比特量化,4比特扇出的数据;空间站Ra为1比特量化,2比特扇出的数据;天空频率4 836 MHz;带宽16 MHz;积分时间为8.192×10-3s。相关处理后的数据规格为60×120×8 192,利用每120×8 192个点的数据为一组进行二维傅里叶变换。由(10)式和(11)式确定时延和时延率方向的搜索步长为
| $ d_{\text {step }}=\frac{N}{10 B}=1.02400 \times 10^{-4} \mathrm{~s} \text {, } $ | (17) |
| $ d r_{\text {step }}=\frac{M}{2 f_0 T}=1.26210 \times 10^{-8} \mathrm{~s} / \mathrm{s}. $ | (18) |
以先验时延模型作为搜索的中心点,时延和时延率搜索的网格大小为20×200,其中,时延的搜索范围为6.336 00×10-3~8.281 60×10-3 s,时延率的搜索范围为1.627 00×10-6~4.138 58×10-6 s/s。算法验证时,首先采用常规多重网格条纹搜索算法,仅使用线性时延模型对每个网格点相关处理,得到峰值点的干涉条纹图;再使用本文的射电源条纹搜索算法构建二次项时延模型;最后对两者的结果比较验证。
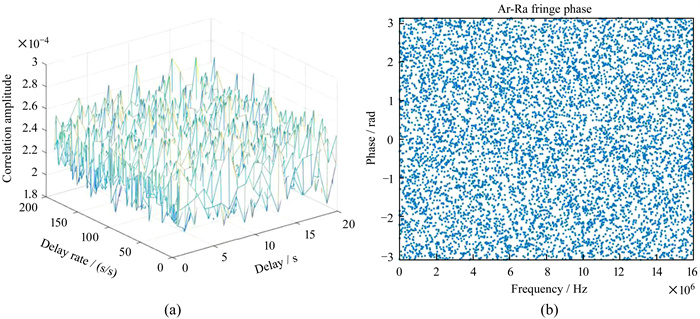
图 4(a)为直接利用线性时延模型进行条纹搜索的相关幅度图,峰值点对应的网格位置为(15, 158),相关幅度为2.869 00×10-4;图 4(b)为峰值点对应的条纹相位。图中没有明显的干涉条纹。
|
| 图 4 使用条纹搜索和线性时延无法得到正确条纹。(a)相关幅度图;(b)干涉条纹图 Fig. 4 Fringe search using linear delay can not produce the fringe.(a)Correlation amplitude; (b)interference fringe |
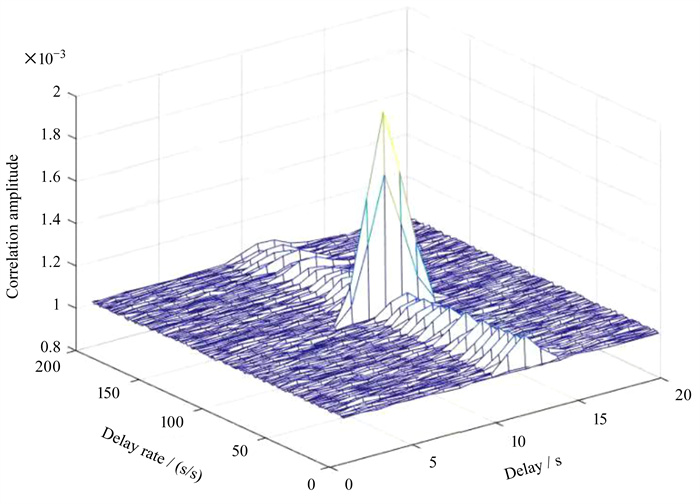
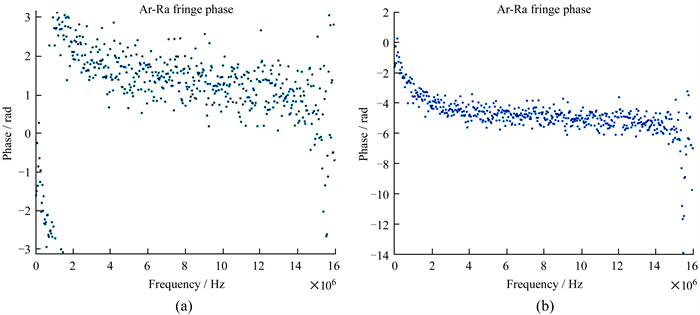
图 5为空间甚长基线干涉测量射电源条纹搜索算法得到的不同网格点对应的相关幅度,峰值点对应的网格位置为(11,101),相关幅度为1.96700×10-3,经过拟合后得到二次项时延系数[7.368 75×10-3 s,2.887 84×10-6 s/s,-4.299 89×10-11 s/s2]。使用该二次项模型做相关处理,可得到图 6(a)的干涉条纹,图 6(b)为解卷绕之后的条纹结果。可见,本文提出的算法在处理RadioAstron数据时优于多重网格条纹搜索算法。
|
| 图 5 二次项时延补偿的相关幅度 Fig. 5 Correlation amplitude using quadratic delay |
|
| 图 6 采用二次项时延补偿后获得清晰的干涉条纹。(a)解卷绕之前的干涉条纹;(b)解卷绕之后的干涉条纹 Fig. 6 Clear interference fringes are obtained by quadratic time delay compensation.(a)Phase wrapping; (b)phase unwrapping |
该算法原理样机在Linux集群平台,采用计算节点间MPI+节点内POSIX多线程的两级并行实现,计算节点的中央处理器型号为英特尔Xeon E5-2620,主频为2 GHz,每个节点的中央处理器个数为12,运行耗时如表 1。后续通过优化,运行速度可以进一步提高。
| Number of nodes*Number of threads | Grid points(delay*delay rate) | Time consumption |
| 10*10 | 20*200 | About 45 minutes |
在未来探月四期任务中,地月空间甚长基线干涉测量试验系统受中继星轨道扰动和设备时延影响,可能导致射电源预报时延模型和实际时延有较大差异。本文在常规多重网格条纹搜索的基础上,根据空间甚长基线干涉测量信号弱的特点,提出了一种适用于空间甚长基线干涉测量的射电源条纹搜索算法。该算法先建立关于时延和时延率的二维搜索网格,使用线性时延相关处理,然后由二维傅里叶变换搜索残余时延和时延率,最后重构二次项时延模型。本文使用RadioAstron数据验证算法,结果表明在使用常规线性时延模型搜索无法实现空地基线条纹的情况下,新算法可以得到清晰的空间甚长基线干涉测量射电源干涉条纹。经进一步测试和完善,该算法可应用于我国后续空间甚长基线干涉测量。
| [1] | BROTEN N W, CLARKE R W, LEGG T H, et al. Diameters of some quasars at a wavelength of 66.9 cm[J]. Nature, 1967, 10: 44–45. |
| [2] |
钱志瀚, 邬林达. 甚长基线干涉测量[M]. 北京: 测绘出版社, 1983: 116-119. QIAN Z H, WU L D. Very Long Baseline Interferometry[M]. Bejing: SinoMaps Press, 1983: 116-119. |
| [3] | LIAO S L, TANG Z H, QI Z X. A model of geometric delay in Space VLBI[J]. Research in Astronomy and Astrophysics, 2014, 14(8): 1029–1036. DOI: 10.1088/1674-4527/14/8/013 |
| [4] |
郑为民, 舒逢春, 张冬. 应用于深空跟踪测量的VLBI软件相关处理技术[J]. 宇航学报, 2008, 29(1): 18–24 ZHENG W M, SHU F C, ZHANG D. Application of software correlator to deep Space VLBI tracking[J]. Journal of Astronautics, 2008, 29(1): 18–24. |
| [5] | ZHANG T Y, MENG Q, CHEN C Y, et al. A model-free CAF fringe search algorithm with wavelet boosting for VLBI observation[J]. Publications of the Astronomical Society of the Pacifific, 2017, 129(977): 074501. DOI: 10.1088/1538-3873/aa6f53 |
| [6] |
孙晓彤, 童力, 郑为民, 等. 基于多重网格的射电源条纹搜索算法研究[J]. 天文研究与技术, 2021, 18(1): 52–59 SUN X T, TONG L, ZHENG W M, et al. Research on radio source fringe search algorithm based on multi-grid[J]. Astronomical Research&Technology, 2021, 18(1): 52–59. |
| [7] | COTTON W D. Fringe-fitting[C]//Proceedings of the ASP Conference Series. 1995: 189-208. |
| [8] | TAKAHASHI F, KONDO T, TAKAHASHI Y, et al. Very Long Baseline Interferometer[J]. Aerospace and Electronic Systems Magazine, 2000, 17(8): 43–44. |
| [9] |
周玉兴, 涂火年, 区丽云. 基于QR分解的线性方程组Ax=b解的结构[J]. 海南大学学报自然科学版, 2013, 31(4): 289–291 ZHOU Y X, TU H N, OU L Y. Structure of solutions of linear equations Ax=b based on QR decomposition[J]. Natural Science Journal of Hainan University, 2013, 31(4): 289–291. |


