引用本文
王晨, 彭朝阳, 陈家明. EP和α “双追踪” GRB 131231A的能谱特性研究[J]. 天文研究与技术, 2022, 19(6): 540-551.  
Wang Chen, Peng Zhaoyang, Chen Jiaming. Study on Energy Spectrum Characteristics of EP and α "Double Tracking" Gamma-ray Bursts[J]. Astronomical Research and Technology, 2022, 19(6): 540-551.  
EP和α “双追踪” GRB 131231A的能谱特性研究
王晨, 彭朝阳, 陈家明     
云南师范大学物理与电子信息学院, 云南 昆明 650500
收稿日期: 2022-01-25; 修订日期: 2022-02-16
基金项目: 国家自然科学基金(12163007)资助
作者简介: 王晨, 男, 硕士研究生, 主要研究伽马射线暴.Email: 1985824135@qq.com.
通讯作者: 彭朝阳, 男, 教授, 主要研究伽马射线暴.Email: pengzhaoyang412@163.com.
摘要: GRB 131231A是一个具有EP和α “双追踪”行为的特殊暴。为了进一步分析该暴的能谱特征, 使用贝叶斯方法做详细的时间分辨光谱分析后发现, 24个分辨谱中16个有明显热成分, 这些热成分主要分布在脉冲的前期和峰值附近, 支持伽马暴喷流从物质主导到磁主导的过渡。加入热成分后参数EP和α都变硬, 而峰值流量Fp几乎不变。使用光球层成分计算相对论流出物的特性参数后发现, 流出物特性参数初始半径r0、饱和层半径rs、光球层半径rph和流出物滑行运动阶段洛伦兹因子Γ均发生较为明显的演化; 温度随时间的演化能用拐折幂律模型拟合, 上升和下降阶段的幂律指数分别为a=7.65 ±3.48和b=-2.10 ±3.48, 下降指数b与前人得出的约-2/3有较大偏差。
关键词: Fermi伽马射线暴    瞬时辐射能谱    光谱拟合    数据分析    最优模型    
Study on Energy Spectrum Characteristics of EP and α "Double Tracking" Gamma-ray Bursts
Wang Chen, Peng Zhaoyang, Chen Jiaming     
College of Physics and Electronic Information, Yunnan Normal University, Kunming 650500, China
Abstract: GRB 131231A is a special Gamma-Ray Burst (GRB) with EP and α possessing the "dual tracking" behavior. To further analyze the energy spectrum characteristics of the burst, we use the Bayesian method to perform a detailed time-resolved spectral analysis and find that 16 of the 24 resolved spectra have significant thermal components, which are mainly distributed in the early and peak stages of the pulse. Near the peak, the transition from matter-dominated to magnetic-dominated GRB jets is supported. After adding thermal components, parameters EP and α become hard, while the peak flux Fp is almost unchanged. We calculate the characteristic parameters of the relativistic flow using the composition of the photosphere, and find that the initial radius r0 of the flow characteristic parameter, the radius of the saturation layer rs, the radius of the photosphere layer rph, and the Lorentz factor Γ during the coast phase of the flow all evolve significantly. The evolution of temperature over time can also be fitted by the inflection power-law model. The power-law index of its rising and falling stages are a=7.65 ± 3.48 and b=-2.10 ± 3.48, respectively. But b has a large deviation from the index value close to -2/3 obtained by previous study of other thermal pulses.
Key words: Fermi Gamma-ray burst    prompt emission    spectral fitting    data analysis    optimal model    

人类研究伽马暴已经有50多年的历史，伽马暴的瞬时辐射在几个基本问题上依然让人感到困惑，一些非常基础的问题是喷流成分(重子主导的火球或是坡印廷流量(Poynting-flux)主导的流出物)，它决定或至少强烈影响能量耗散机制(激波或磁重联)、粒子加速机制(热主导或磁主导)，特别是辐射机制(同步辐射) 或光球准热辐射的康普顿化[1]。伽马暴辐射有瞬时辐射和余辉两个主要阶段。瞬时辐射阶段通常持续几秒到几分钟。伽马暴瞬时辐射具有丰富的观测特征，但是其中的大多数没有合理的解释。伽马暴瞬时辐射阶段的光谱成分主要来自两种起源：同步辐射(非热成分)和光球层(热成分) [2]。过去的研究表明，伽马暴能谱中可能存在3种基础成分[3]：(1) 能用Band函数拟合的非热成分；(2) 能用普朗克函数拟合的热成分；(3) 出现在能量较高区域的幂律成分。目前已观测到的伽马暴中能发现两种或两种以上的成分[4]。热成分主导的伽马暴非常稀少，所以对于暴的能谱处理时多采用组合模型，常用的基础模型是Band函数或者截止幂律(Power law with exponential cut off; CPL) 函数。多数情况下，组合模型能得到更优的参数值，有助于我们推断伽马暴能源机制和中心引擎。在BATSE探测器时期，Ep显示出几种不同的演化：(1)“从硬到软”的趋势，无论流量如何升降，它都是单调递减的[5-6]；(2)“流量跟踪”趋势，即参数的演化跟随流量上升或下降[7]；(3)“软到硬”的趋势或混乱的演变[8]。2008年费米(Fermi) 卫星升空后，大量的伽马暴观测数据证实前两种模式占主导地位：“由硬到软”约占三分之二，“流量跟踪”约占三分之一[9]。这些演化模式的物理起源仍然没有解决，尽管文献中已经提出了一些方案[10-11]。与Ep演化相比，α演化更加混乱，因此研究和物理解释相对较少。文[9]发现GRB 131231A的Ep和α演化都表现出“通量跟踪”行为，并且定义为光谱演化的“双跟踪”模式[9]，但文[9]并没有加入热成分进行详细的能谱分析。既然很多研究表明伽马暴能谱中包含热成分，为了更详细地研究光谱参数EP和α “双追踪”的能谱特性，我们使用贝叶斯分区并使用蒙特卡罗模拟方法处理GRB 131231A。在伽马暴的研究中，研究人员发现次主导的热成分，一般出现在Band谱[12]的左侧[13]，即热成分一般出现在低能Band谱区域。针对这种现象，文[9]在探究8个具有较明显热成分的伽马暴中热成分对于非热成分几个特征参数值的影响时，都选用截止幂律函数作为基础模型与普朗克函数(Blackbody, BB) 模型组合进行探究[2]。对于绝大多数伽马暴的时间分辨谱，截止幂律函数模型是适合的[14-15]。然而在一些例子中，Band模型的高能幂律指数β显著提高拟合。在同步辐射的情况下，高能幂律指数β提供了有关粒子加速和激波的本质，而在光球辐射的情况下，它提供了有关辐射区域能量耗散的信息[16]。考虑到这种情况，我们以统计值BIC (Bayesian Information Criterion) 作为判断标准[17]，对伽马暴的每个拟合区间选用最优模型的数据，并研究使用最优模型之后GRB 131231A能谱参数的变化情况。

1 数据处理和分析方法

GRB 131231A由费米卫星中的伽马暴探测器(8 keV~40 MeV)于2013的12月31触发。本文中，我们使用贝叶斯分析包，即最大似然工作框架(3ML) 分析所有伽马暴的光谱。该工具包采用马尔可夫链蒙特卡罗理论(Markov Chain Monte Carlo, MCMC) 对时间分辨谱进行处理, 这种方法的优点详见文[1]。我们从网站(https://fermi.gsfc.nasa.gov/)获取伽马暴探测器[18]三种类型的数据，CTIME文件、CSPEC文件和TTE文件，选择具有最小时间分辨率(2 μs)的TTE文件进行数据分析。在贝叶斯统计的马尔可夫链蒙特卡罗拟合例子中，为了确定能谱拟合的最优模型，我们选取BIC[17]作为判断标准，通过比较不同模型BIC的差值(ΔBIC)确定最佳模型。一般来说，Band模型[12]和截止幂律函数模型[19]在伽马暴拟合时是两种较为优越的模型，我们把这两种模型选作基础模型，分别与普朗克函数模型组合，在伽马暴时间分辨谱的每一个区间经过模型对比，进而选出适应该区间的最优模型。为了更好地研究光谱随时间的演化，对光谱进行时间分辨谱分区是一种有效的研究方法。文[20]研究了4种对光变曲线分区时间片的工具，其中信噪比(S/N)和贝叶斯分区(BBs) [21]是两种最有效的分区方法。这两种方法各有优缺点，传统的信噪比分区可以确保每个时间段能分到足够多的光子做光谱拟合，但是有时它会破坏物理结构。关于贝叶斯分区的优缺点详见文[20]，我们采用贝叶斯分区，但是依然使用信噪比作为一种筛选方法剔除所得区间中不满足某一标准的区间(本文选取信噪比S/N≥20的区间，因为信噪比S/N < 20的区间拟合时出现较大误差[1])，共同使用这两种方法，我们可以得到更有研究意义的区间。表 1给出了该暴的相关参数，注：CPL1代表ΔBIC≤-8的时间分辨谱区间使用截止幂律函数模型，CPL2代表-8 < ΔBIC < 8的时间分辨谱区间使用截止幂律函数模型。图 1给出了一个分辨谱的拟合结果。

表 1 伽马暴参数及使用的探测器编号 Table 1 Gamma-ray burst parameters and detector numbers used
GRBs T90/s Detector Total
of bins		 Number of
bins with
thermal
component		 Number of
bins suitable
for CPL1
(ΔBIC-8)		 Number of
bins suitable
for CPL2
(-8 < ΔBIC < 8)		 Number of
bins suitable
for Band
(8≤ΔBIC)
131231A 31.232 n0, n3, n4, b0 24 16 0 11 5
表选项
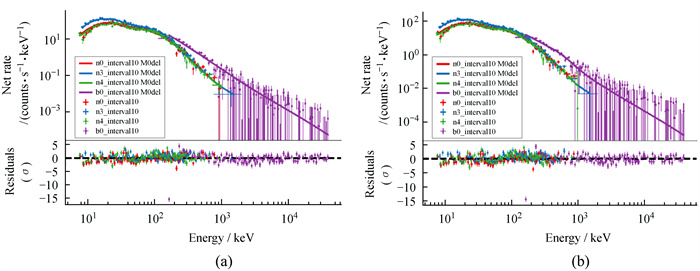
图 1 一个黑体成分最显著的计数率时间分辨谱(时间区间为24.59~25.86) 拟合结果。(a) Band函数模型；(b) Band函数模型+普朗克函数模型 Fig. 1 Example of count spectral fit results with the most significant black body components in the time bin 24.59 s-25.86 s.(a) Band model; (b) Band+BB
图选项
2 分析结果

我们使用Band函数模型、康普顿函数模型和普朗克函数模型对GRB 131231A进行拟合，得到它的时间分辨谱数据。从时间分辨谱的ΔBIC来看，有些暴的某些时间段中截止幂律函数模型的拟合结果优于Band函数模型，有些结果相反。综合考虑之后我们把每个暴的每个时间分辨谱区间进行最优模型选择，选择方法是用每个区间单独用截止幂律函数模型拟合时产生的BIC减去单独用Band函数模型拟合时产生的ΔBIC作为筛选标准，当ΔBIC≤-8时我们认为该区间更适合使用截止幂律函数模型，当ΔBIC≥8时我们认为该区间更适合使用Band函数模型，当-8＜ΔBIC＜8时我们认为该区间更适合使用截止幂律函数模型(当两种模型中任何一种模型优势不明显时，一般选用参数少的模型)。然后再使用该区间选定基础模型的BIC与基础模型加普朗克函数模型的组合模型的BIC差值是否≥8判断该区间是否有热成分，最后筛选信噪比S/N≥20的区间作为研究对象。

光谱分析得到单个时间区间的时间跨度远小于整体的时间跨度，我们假设在每个时间区间中参数的变化是准静态的，用时间区间中值时刻参量的特征代表整个时间区间参数的行为[22]。

2.1 参数的分布

图 2显示了Best模型参数分布，包括α, Ep和Fp。表 2列出了分布的平均值和标准偏差。我们对各个参数分布采用高斯函数核进行核密度估计，结果如表 2。未加入黑体成分和加入黑体成分时，低能光子指数α分布的均值分别为-1.06±0.29和-1.00±0.29，加入黑体成分后，α轻微变硬，但与典型值α~-1基本一致，且没有超过所谓的同步“死线”(-3/2＜α＜-2/3) [23]。在加入黑体成分后，峰值能量EP的核密度曲线峰值向右偏移，均值为199.84±161.61，与未加入黑体成分相比，峰值能量Ep变硬。加入黑体前后Fp没有明显变化，平均值仅有微弱变化，这些结果和前人的研究结果一致。

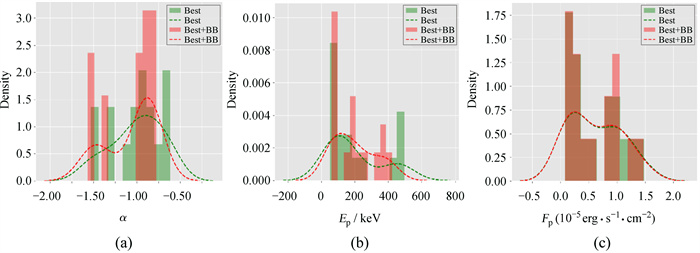
图 2 Best模型的参数α，EP和FP分布 Fig. 2 The distribution of the parameter values α, EP and FP
图选项
表 2 模型参数均值与标准偏差 Table 2 Mean and standard deviation of model parameters
Model α Ep/keV FP/erg·s-1·cm-2
Best -1.06±0.29 196.96±124.82 (6.11±4.57)×10-6
Best+BB -1.0±0.29 199.84±161.61 (6.17±4.62)×10-6
表选项
2.2 加入黑体前光谱参数的演化

我们用本文分析的数据重新分析未加入黑体成分的峰值能量和低能谱指数的演化情况。图 3展示了贝叶斯区间中S/N≥20的时间分辨谱区间对应的数据点。GRB 131231A的参数EP和α表现为较好的“流量跟踪”趋势，本文的结果与文[9]的结果一致。

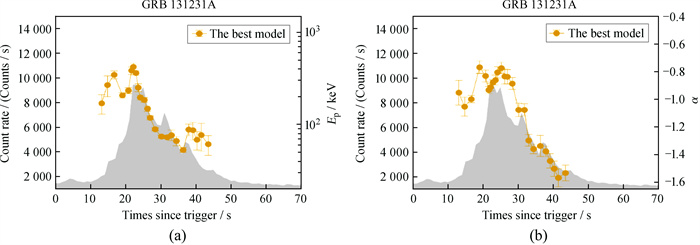
图 3 GRB 131231A最优模型的时间分辨谱参数EP和α的分布 Fig. 3 The distribution of the parameter values EP and α of the time-resolved spectrum of the optimal model of GRB 131231A
图选项
2.3 加入热成分后光谱参数的演化

加入黑体成分后，我们找出探测到热成分的16个时间分辨谱区间发现，Ep和α的演化趋势和未加入热成分的趋势一致，依然表现出双追踪行为。这两个参数发生了变化，α和Ep轻微变硬，但从图 4中我们能发现这两个参数变化的细节，GRB 131231A中有热成分的区间EP值的整体变化并不一致，如图 4 (a)。我们发现GRB 131231A中EP在峰值之前，加入普朗克成分后变硬(值变大)；峰值之后，加入普朗克成分后变软(值变小)。其中EP变硬的点有6个，均分布在峰值之前；EP变软的点有10个，均分布在峰值之后。GRB 131231A中α的整体变化也不一致，如图 4 (b)。有一个点分布在同步辐射死线之上，其余点分布在同步辐射死线之下，加入普朗克成分后，α出现了明显的变化，在峰值之前，加入普朗克成分后α值变软；峰值之后，加入普朗克成分后变硬。在加入黑体成分前，GRB 131231A中仅有最后两个点的α值小于-3/2；加入热成分之后，脉冲峰值处有两个点的α值上升到超过同步辐射死线，最后两个点的α值略有上升，但是依然小于-3/2。

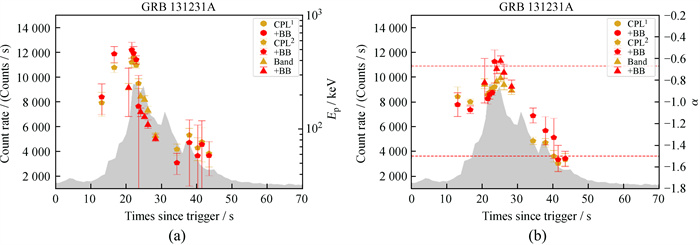
图 4 (a) GRB 131231A中探测到热成分的时间分辨谱区间中EP和α的分布；(b) 上下两条红色虚线分别代表α=-2/3和α=-3/2的位置 Fig. 4 (a) Distribution of EP and α in the time-resolved spectral interval of thermal components detected in GRB 131231A; (b) the upper and lower red dashed lines represent α=-2/3 and α=-3/2
图选项
2.4 光谱参数的相关性

相关分析在理解伽马暴物理学中起着重要作用，因为它提供了一些线索帮助我们揭示伽马暴的本质。我们探究了参数logEP-logFP，logFP-α和logEP-α的关系，表 3给出了具体相关系数。相关强度由斯皮尔曼相关系数r给出，强相关性r>0.7，弱相关性r < 0.4。文[7, 24-25]揭示了logF-α的关系主要有3种类型：非单调关系(包含正和负幂律段，在峰值流量处具有明显的间断)、单调关系(由单个幂律描述) 和没有明显的趋势。GRB 131231A 3种模型中logEP-logFP的相关性，Best为r=0.426, p=0.037 8；Band为r=0.687, p<10-4；CPL为r=0.566, p<10-4，最好的是Band模型。3种模型中logEP-α的相关性，Best为r=0.412, p=0.045 3；Band为r=0.70, p=0.000 14；CPL为r=0.731, p<10-4，最好的是Band模型。3种模型中logFP-α的相关性，Best为r=0.765, p<10-4；Band为r=0.655, p=0.000 52；CPL为r=0.756, p<10-4，最好的是Best模型。在Band和CPL模型中logEP-logFP，logFP-α和logEP-α都表现出极强的相关性。当我们使用Best模型时，logEP-logFP和logEP-α的相关性均变弱；logFP-α相关性强于Band函数和截止幂律函数。

表 3 GRB 131231A在不同模型中EP-Fp，EP-α和Fp-α参数关系(斯皮尔曼(Spearman)相关性系数r和置信度p) Table 3 GRB 131231A parameter relationship of EP-Fp, EP-α and Fp-α in different models (Spearman correlation coefficient r and confidence p)
Model EP-FP EP-α FP-α
r p r p r p
Best 0.426 0.037 8 0.412 0.045 3 0.765 < 10-4
Best+BB 0.332 0.208 0.065 0.812 0.738 0.001
Band 0.687 0.000 21 0.70 0.000 14 0.655 0.000 52
Band+BB 0.444 0.085 0.476 0.062 0.871 < 10-4
CPL 0.566 0.003 9 0.731 < 10-4 0.756 < 10-4
CPL+BB 0.368 0.161 -0.082 0.762 0.70 0.003
表选项
2.5 热成分分析

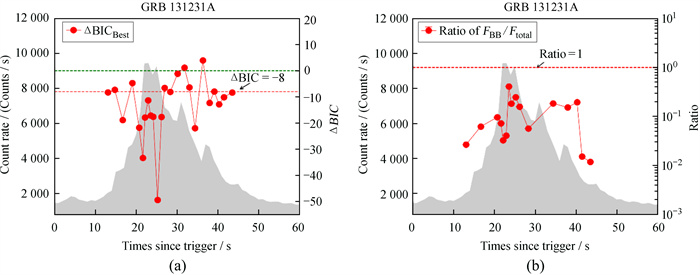
为了检查能谱中的热成分，我们先寻找对应于时间分辨谱的最优模型，用最优模型加入普朗克函数成分拟合，查看加入黑体前后统计量的差值ΔBIC，如果ΔBIC < -8说明光谱中显著含有热成分。图 5 (a)给出了ΔBIC在脉冲中的演化和分布图，图 5 (b)给出了热成分流量与总能量流量的比率。

图 5 (a) ΔBIC随脉冲的演化和分布图，绿色和红色虚线分别表示ΔBIC等于0和-8的位置；(b) 探测到热成分的光谱中热成分流量与总能量流量的比率，红色虚线代表比率为1 Fig. 5 (a) The evolution and distribution of ΔBIC with pulse, and the green and red dotted lines represent the positions where ΔBIC is equal to 0 and -8 respectively; (b) the ratio of thermal component flow to total energy flow in the spectrum of detected thermal component, and the red dotted line represents the ratio of 1
图选项

GRB 131231A具有明显的脉冲上升阶段和下降阶段。我们对GRB 131231A中出现热成分的区域进行统计，从图 5 (a)统计的结果来看，ΔBIC < -8的光谱主要出现在对应高光子计数的光变曲线的位置，说明热成分主要存在于脉冲前期，并且随着时间逐渐减少。图 5 (b)表明，热成分流量与总能量流量的比率多数分布在0.1以下，比率较高的区域主要分布在高脉冲区域。

2.6 与热成分相关的参数

现有的研究表明，热成分起源于光球层，根据高纬辐射解释，最高温度和最强热流最初从光球层辐射轴发出，并朝向观测者。因此，原则上来说，光子辐射位置的半径可以确定[26]。按照文[26]的理论，对于一个已知红移的伽马暴，知道该暴的观测温度和热能量流量时，我们可以计算流出物的初始半径r0 (从中心引擎到喷流喷射处的距离)，对于rph> rs的情况可以更进一步计算伽马暴的饱和层半径rs、光球层半径rph和流出物滑行运动阶段洛伦兹因子Γ。根据文[22]中(1) 式可以判断光球层和饱和层的相对位置，我们发现GRB 131231A中有热成分区间均满足(FBB/FNT)-3/2>1，判定这个暴的所有壳层的光球层位于饱和层之上(rph> rs)，应用文[26]中的理论计算这个暴的初始半径r0、饱和层半径rs、光球层半径rph和流出物滑行运动阶段洛伦兹因子Γ。

我们能得到与热成分相关的参数$\Re, \Re$可以解释为辐射区的有效横向尺度[22]，$\Re$为常数意味着光球的有效辐射区域与时间无关。我们可以通过

$ \Re=\left(\frac{F_{\text {вв }}}{\sigma_{\mathrm{SB}} T^4}\right)^{1 / 2}=1.06 \frac{(1+z)^2}{d_{\mathrm{L}}} \frac{r_{\mathrm{ph}}}{\varGamma} $ (1)

计算得到伽马暴的$\Re$值，其中，σSB为斯特藩-玻尔兹曼常量，单位为$\mathrm{erg} \cdot \mathrm{s}^{-1} \cdot \mathrm{cm}^{-2} \cdot \mathrm{K}^{-4} ; F_{\mathrm{BB}}$为观测到的黑体能量流量，单位为$\mathrm{erg} \cdot \mathrm{s}^{-1} \cdot \mathrm{cm}^{-2} ; T$为黑体的绝对温度，单位为keV；z为伽马暴的宇宙学红移；dL为光度距离，单位为cm；Γ为流出物滑行阶段的洛伦兹因子。

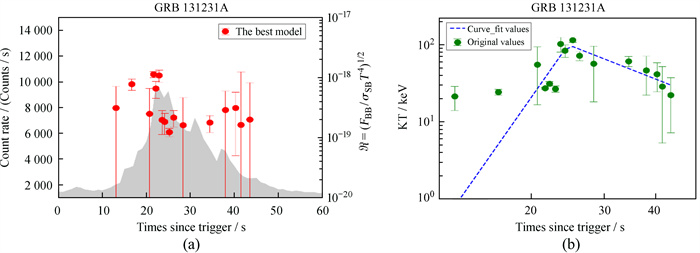
如图 6 (a)，在脉冲起始阶段$\Re$表现为快速上升，在22 s后$\Re$没有表现出单调递增的趋势，变化较为平缓。流出物速度方向与视线的夹角为θ，在脉冲峰值时刻之后，θ=0区域的辐射减弱，高纬辐射起主导作用[26]，此时光球的有效辐射区域与时间无关。

图 6 (a) $\Re$随脉冲的演化图；(b) 探测到热成分的光谱中温度随脉冲的演化，蓝色虚线为拟合线 Fig. 6 (a) The evolution of $\Re$ with pulse; (b) the evolution of temperature with pulse in the spectrum of detected thermal components, and the blue dotted line is the fitting line
图选项

为了分析温度随时间的演化，文[27]依据文[28]的拐折幂律模型派生了一种模拟温度的拐折幂律模型。拐折幂律的形式如文[27]中(6)式，我们使用它拟合该暴探测到热成分区间的温度时间，如图 6 (b)。我们得到对应于(6)式的参量拟合值分别为Φ=2.77±2.44，t0=24.59±0.95，ξ=-4.88±2.49和δ=0.0028±1.08；由拟合参量我们得到拐折幂律函数的上升和下降阶段幂律指数分别为a=7.65±3.48和b=-2.10±3.48。

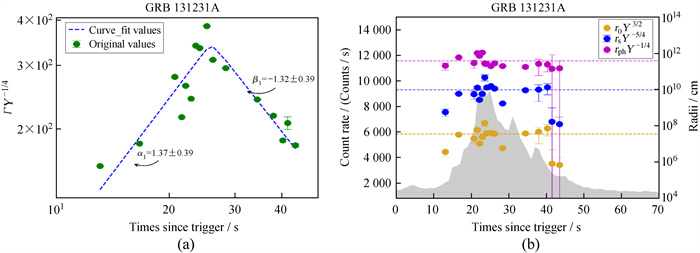
GRB 131231A的洛伦兹因子呈现先上升后随时间衰减的演化趋势，起始值为157±0.5，峰值为385.6±0.34。它能用拐折幂律较好地拟合，如图 7 (a)，上升阶段的幂律指数α1=1.37±0.39，下降阶段的幂律指数β1=-1.38±0.39。文[22, 29]发现在具有显著光球成分的伽马暴中，洛伦兹因子随时间单调减小，$\varGamma \propto(F / R)^{1 / 4} Y^{1 / 4}$。在脉冲上升阶段，总流量F和$\Re$的增加速率几乎相同，洛伦兹因子接近固定值或仅随时间微弱衰减。我们得到的洛伦兹因子呈现为先增加后衰减，与传统光球模型预言的洛伦兹因子在初始阶段近似为常数不符。

图 7 GRB 131231A的Γ，r0，rs和rph的演化 Fig. 7 The evolution of Γ, r0, rs and rph of GRB 131231A
图选项

初始半径表示喷流开始加速。在GRB 131231A中r0从初始值$\left(3.6 \times 10^6 \pm 1.56 \times 10^6\right) Y^{3 / 2} \mathrm{~cm}$开始随光变曲线上升，在脉冲峰值处(22 s)达到最大值$\left(1.39 \times 10^8 \pm 5.17 \times 10^7\right) Y^{3 / 2} \mathrm{~cm}$，但是并没有很好地追踪光变曲线；脉冲峰值后，r0又呈现上升的趋势，这可能是由于中心引擎的再活动导致；在脉冲后期，r0下降至$\left(6.9 \times 10^5 \pm 1.02 \times 10^6\right) Y^{3 / 2} \mathrm{~cm}$，低于初始值。r0的变化量级分布在106~108，这个演化范围在黑洞的视界半径与Wolf-Rayet前身星的核心大小之间，表明r0与喷流和前身星之间的相互作用有关[22, 29]。

饱和层半径rs的演化与初始半径在脉冲中的行为相似，在数值上相差近3个数量级。rs初始值为$\left(5.7 \times 10^8 \pm 2.46 \times 10^8\right) Y^{-5 / 4} \mathrm{~cm}$，最大值为$\left(4.72 \times 10^{10} \pm 1.76 \times 10^{10}\right) Y^{-5 / 4} \mathrm{~cm}$，演化过程中的最小值为$\left(1.2 \times 10^8 \pm 1.83 \times 10^8\right) Y^{-5 / 4} \mathrm{~cm}$。

光球层是可以观察到光子的最深区域。在脉冲起始至达到峰值阶段(22 s)，光球层半径rph呈现跟随脉冲上升(追踪的趋势)，从初始值$\left(2.06 \times 10^{11} \pm 8.68 \times 10^{10}\right) Y^{-1 / 4} \mathrm{~cm}$在近似脉冲峰值处达到最大值$\left(1.1 \times 10^{12} \pm 5.89 \times 10^{10}\right) Y^{-1 / 4} \mathrm{~cm}$；脉冲峰值后，rph快速下降，变化范围在一个量级内，之后仅微弱变化。GRB 131231A的光球层半径最小值为$\left(1.41 \times 10^{11} \pm 6.87 \times 10^{11}\right) Y^{-1 / 4} \mathrm{~cm}$。脉冲下降阶段rph变化与GRB 110721A[22]，GRB 140329B 和 GRB 160625B[1]一致，$r_{\mathrm{ph}} \propto \frac{L_0}{\varGamma^3} \propto \frac{M}{\varGamma^2}, L_0$为伽马暴总的运动学光度，Μ是重子载量，Μ=L0/Γc2，rph的变化与洛伦兹因子Γ和Μ有关。脉冲上升阶段，rph随脉冲上升，Γ也随时间增加，这要求L0或Μ要以更快的速率增加，而重子载量的增加，导致与它相关的电子增加了不透明度，从而增加了光球层半径。在脉冲衰减阶段，Γ和L0都减小，而rph保持常数或仅微弱变化，在这种状况下，满足$L_0 \propto \varGamma^3\left(\text { 或 } M \propto \varGamma^2\right)$[29]。

3 结论与讨论

GRB 131231A是一个比较明亮且较为接近单脉冲的长暴。我们应用贝叶斯方法，利用经验光谱模型和物理模型，即截止幂律函数模型、Band函数模型和普朗克函数模型，进行详细的时间分辨谱分析，并在每个时间分辨谱区间上进行模型比较，确定适合某一区间的最优模型，我们总共获得了24个光谱并研究了它们的性质，这些光谱的最佳模型的拟合参数见表 4。这个伽马暴的EP和α都表现为较好的追踪行为。EP的流量追踪行为可能与两种同步辐射模型有联系[8, 30]。图 2 (b)中显示α均分布于同步辐射死线之下，整体分布非常符合同步辐射模型。文[9]指出，在上升阶段，α变得更硬，表明电子正在从快速冷却区向慢速冷却区演化[9]。在衰减阶段，α变得更软，宽脉冲的衰减阶段可能由“曲率效应”控制[31-33]。

表 4 伽马暴131231A最优模型拟合的时间分辨谱 Table 4 The best fitting results of models to fit the time-resolved spectrum of GRB 131231A
Tstart: Tend Models S/N α EP
/keV		 kT/keV FP
/(erg·s-1·cm-2)		 FBB
/(erg·s-1·cm-2)		 BIC
12.0:14.17 CPL2 29 -0.95-0.09+0.09 162.28-27.1+24.9 7.46×10-3.35×10-8-7+3.75×10-8 3 192
CPL2+BB -1.02-0.11+0.11 196.4-50.0+37.0 21.32-8.10+7.28 7.62×10-4.01×10-8-7+4.34×10-8 2.03×10-1.75×10-8-8+4.49×10-8 3 184
14.17:15.32 CPL2 31 -1.05-0.07+0.07 284.02-52.6+52.0 1.36×10-6.90×10-8-6+7.26×10-8 2 331
CPL2+BB -1.09-0.08+0.08 329.6-82.1+76.4 22.72-7.62+6.91 1.37×10-7.16×10-8-6+7.58×10-8 3.07×10-2.62×10-8-8+5.67×10-8 2 324
15.32:18.03 CPL2 85 -1.0-0.03+0.03 346.34-25.0+25.0 3.29×10-6.15×10-8-6+6.12×10-8 3 903
CPL2+BB -1.07-0.04+0.03 492.7-64.1+66.8 24.20-2.18+2.15 3.38×10-6.02×10-8-6+5.68×10-8 2.10×10-4.93×10-8-7+4.89×10-8 3 885
18.03:20.08 Band 108 -0.77-0.05+0.05 207.34-14.0+14.0 4.93×10-5.71×10-8-6+5.92×10-8 3 564
Band+BB -1.04-0.06+0.06 388.3-306.31+309.46 25.34-1.72+1.87 5.08×10-9.47×10-7-6+9.82×10-8 4.62×10-1.33×10-7-7+1.05×10-7 3 560
20.08:21.35 Band 102 -0.83-0.04+0.04 233.60-17.0+17.0 5.89×10-7.87×10-8-6+8.36×10-8 2 934
Band+BB -0.81-0.19+0.21 234.4-105.7+107.6 54.95-31.4+38.3 5.95×10-1.01×10-7-6+1.14×10-7 5.73×10-2.42×10-7-7+1.04×10-6 2 912
21.35:21.91 CPL2 85 -0.93-0.03+0.03 360.86-26.0+26.0 9.50×10-1.83×10-7-6+1.89×10-7 1 811
CPL2+BB -0.97-0.05+0.03 481.0-47.5+64.5 27.13-4.55+5.15 9.65×10-1.67×10-7-6+1.78×10-7 7.01×10-1.47×10-7-7+1.55×10-7 1 777
21.91:22.41 CPL2 94 -0.91-0.03+0.03 389.18-26.0+26.0 1.25×10-2.07×10-7-5+2.16×10-7 1 754
CPL2+BB -0.93-0.04+0.03 435.0-38.2+51.6 31.10-7.08+2.11 1.25×10-2.02×10-7-5+1.99×10-7 4.09×10-2.47×10-7-7+2.31×10-7 1 736
22.41:23.41 CPL2 159 -0.87-0.02+0.02 322.88-13.0+13.0 1.47×10-1.62×10-7-5+1.65×10-7 3 014
CPL2+BB -0.91-0.02+0.02 375.44-22.08+22.8 26.65-2.56+2.47 1.48×10-1.56×10-7-5+1.55×10-7 6.01×10-1.62×10-7-7+1.59×10-7 3 003
23.41:23.72 CPL2 83 -0.86-0.04+0.04 220.87-15.0+15.0 1.02×10-2.19×10-7-5+2.23×10-7 1 188
CPL2+BB -0.63-0.20+0.11 115.3-31.4+90.6 102.1-56.4+21.9 1.05×10-2.52×10-7-5+2.60×10-7 4.28×10-3.50×10-6-6+4.73×10-7 1 171
23.72:24.59 Band 125 -0.81-0.04+0.04 196.32-11.0+11.0 9.09×10-1.11×10-7-6+1.21×10-7 2 480
Band+BB -0.69-0.05+0.06 143.9-15.2+8.5 83.71-9.14+15.2 9.13×10-1.28×10-7-6+1.25×10-7 1.67×10-5.04×10-7-6+4.42×10-7 2 462
24.59:25.87 Band 165 -0.77-0.04+0.04 185.0-11.0+11.0 1.05×10-9.60×10-8-5+9.43×10-8 3 315
Band+BB -0.61-0.04+0.04 129.97-5.7+5.7 114.7-7.79+7.89 1.08×10-1.38×10-7-5+1.31×10-7 2.66×10-3.71×10-7-6+4.10×10-7 3 266
25.87:26.54 Band 110 -0.83-0.05+0.05 148.44-10.0+10.0 8.06×10-1.72×10-8-6+1.23×10-7 2 062
Band+BB -0.72-0.07+0.07 110.9-10.0+9.0 71.8-8.94+9.98 7.99×10-1.23×10-7-6+1.27×10-7 1.26×10-3.76×10-7-6+3.58×10-7 2 044
26.54:27.39 Band 111 -0.84-0.04+0.04 118.37-6.0+6.0 6.42×10-9.42×10-8-6+9.98×10-8 2 281
Band+BB -0.84-0.04+0.05 114.9-9.6+8.5 35.84-20.9+27.4 6.42×10-1.01×10-7-6+9.30×10-8 4.55×10-4.18×10-8-8+3.45×10-7 2 275
27.39:29.31 Band 149 -0.89-0.04+0.04 88.81-3.4+3.4 4.84×10-5.45×10-8-6+5.39×10-8 3 529
Band+BB -0.85-0.05+0.05 83.4-5.5+6.0 56.74-40.2+38.7 4.82×10-6.81×10-8-6+6.14×10-8 2.72×10-2.66×10-7-7+7.16×10-7 3 521
29.31:31.01 Band 128 -1.08-0.05+0.05 73.88-2.86+2.86 3.65×10-5.48×10-8-6+5.01×10-8 3 142
Band+BB -1.01-0.09+0.12 66.3-12.6+8.3 28.62-11.9+9.48 3.64×10-5.68×10-8-6+5.55×10-8 7.97×10-7.40×10-8-7+2.84×10-7 3 141
31.01:32.61 Band 144 -1.08-0.05+0.05 72.54-2.63+2.73 4.22×10-5.6×10-8-6+5.46×10-8 3 193
Band+BB -1.01-0.09+0.09 65.0-7.6+7.3 35.0-14.7+12.6 4.19×10-6.29×10-8-6+6.29×10-8 1.84×10-1.72×10-8-7+2.31×10-7 3 194
32.61:33.45 CPL2 91 -1.29-0.04+0.04 109.1-8.21+8.10 3.22×10-5.64×10-8-6+5.43×10-8 2 025
CPL2+BB -1.28-0.06+0.06 102.7-17.8+14.0 30.47-16.2+23.6 3.22×10-5.67×10-8-6+4.08×10-8 3.18×10-2.83×10-8-8+2.65×10-7 2 019
33.45:35.41 CPL2 113 -1.36-0.04+0.04 103.6-6.3+6.2 2.35×10-3.07×10-8-6+3.21×10-8 3 373
CPL2+BB -1.13-0.2+0.2 57.9-6.22+6.4 60.93-8.60+9.16 2.38×10-4.41×10-8-6+4.47×10-8 4.41×10-8.16×10-8-7+8.47×10-8 3 351
35.41:37.26 Band 87 -1.34-0.05+0.05 52.97-3.65+3.55 1.88×10-4.05×10-8-6+4.01×10-8 3 091
Band+BB -1.27-0.13+0.13 40.4-7.9+10.3 24.80-3.50+4.23 1.87×10-4.13×10-8-6+4.22×10-8 1.40×10-1.19×10-8-7+8.30×10-8 3 095
37.26:38.65 CPL2 94 -1.37-0.05+0.04 141.5-11.+12.0 2.55×10-4.22×10-8-6+4.62×10-8 2 767
CPL2+BB -1.27-0.13+0.13 103.5-42.5+36.6 46.44-30.12+24.37 2.55×10-4.71×10-8-6+5.0×10-8 3.91×10-3.86×10-7-7+2.07×10-7 2 755
38.65:39.61 CPL2 64 -1.44-0.05+0.05 156.31-19.0+19.0 1.98×10-5.04×10-8-6+5.53×10-8 2 116
CPL2+BB -1.44-0.06+0.06 148.9-22.9+25.8 26.89-13.34+16.07 1.97×10-4.79×10-8-6+5.22×10-8 2.37×10-2.09×10-8-8+1.04×10-7 2 108
39.61:40.98 CPL2 64 -1.50-0.05+0.05 137.1-17.4+16.0 1.48×10-3.54×10-8-6+3.62×10-8 2 525
CPL2+BB -1.32-0.20+0.20 86.8-38.34+51.69 41.34-24.7+16.9 1.47×10-3.58×10-8-6+3.83×10-8 2.87×10-2.81×10-7-7+1.15×10-7 2 512
40.97:42.01 CPL2 44 -1.56-0.05+0.05 178.3-33.2+32.6 1.20×10-4.35×10-8-6+4.54×10-8 2 056
CPL2+BB -1.53-0.11+0.13 156.5-74.7+52.8 28.67-15.99+23.38 1.20×10-4.12×10-8-6+4.88×10-8 1.81×10-1.58×10-8-8+2.36×10-7 2 046
42.01:45.0 CPL2 58 -1.53-0.05+0.05 130.8-17.0+16.0 8.35×10-2.09×10-8-7+2.14×10-8 3 647
CPL2+BB -1.5-0.08+0.07 122.5-24.5+24.0 22.2-11.1+15.0 8.31×10-1.98×10-8-7+2.15×10-8 9.81×10-8.58×10-9-9+5.57×10-8 3 638
表选项

通过最优模型与普朗克函数模型的共同拟合，我们探测到16个有明显热成分的时间分辨谱区间，该暴不是热主导的伽马暴。文[9]系统研究了8个含有热成分伽马暴的能谱特性[1]，对于非热成分主导的伽马暴，加入热成分后，α值变软，Ec变硬，能量流量Fp在不同模型中没有明显的不同。对于GRB 131231A，在光变曲线峰值之前，加入普朗克成分后EP变硬，峰值之后，加入普朗克成分后EP变软；在光变曲线峰值之前，加入普朗克成分后α变软，峰值之后，加入普朗克成分后变硬。GRB 131231A具有特殊的光谱演化。

伽马暴喷流的中央引擎很可能是一个混合系统，既有一个热的火球成分，又有一个冷的坡印廷流量成分[34]。一些明亮的暴(例如GRB 090902B) 在脉冲开始处或峰值附近表现出类似热的时间分辨谱，在随后的脉冲中出现非热的时间分辨谱，这可能表明喷流成分在逐渐变化[35]。文[34]在解释伽马暴喷流成分的起源方面做了更全面的描述，即混合喷流模型。文[9]使用此模型分析了8个费米伽马暴[1]，发现大多数爆发可以用混合喷流模型很好地解释。GRB 131231A的低能光子指数α的值不超过所谓的同步辐射死线；但加入热成分后，拟合统计量明显改善，其中ΔBIC < -8的光谱主要集中在脉冲开始阶段和峰值阶段(10~26 s)，随后热成分逐渐减少，说明伽马暴可能从物质主导火球过渡到磁主导的坡印廷流量；在脉冲后期又出现热成分，这可能由中心引擎再活动导致。

虽然温度也能用拐折幂律拟合，但是与文[27]拟合伽马暴中热脉冲得到的上升阶段和下降阶段的指数值均存在较大差异。

我们计算了与热成分相关的参数Γ，r0，rs和rph，得到的洛伦兹因子先增加后衰减，与传统光球模型预言的洛伦兹因子在初始阶段近似常数不符[22, 29]，之后以指数衰减，这可能是因为内激波模型导致[36]。另一种解释是孤立磁星诞生的情况，此时洛伦兹因子随时间增加[37]，但是GRB 131231A的光度远大于磁星模型的光度，所以磁星模型的设想不太可能成立。我们得到r0，rs和rph的变化范围与具有显著光球成分的伽马暴GRB 081224A，GRB 090719A 和 GRB 100707A等[22, 29]变化范围吻合。其中，r0的演化范围在黑洞的视界半径与Wolf-Rayet前身星的核心大小之间，表明r0与喷流和前身星之间的相互作用有关[29]。rs的演化行为与r0近似，在数值上相差3个数量级以内。在脉冲起始至达到峰值阶段(22 s)，光球层半径rph呈现跟随脉冲上升(追踪)；脉冲峰值后，rph快速下降，变化范围在一个量级内，之后仅微弱变化。脉冲的上升阶段，rph随脉冲上升，Γ也随时间增加，这要求L0或Μ以更快的速率增加，而重子载量的增加，导致与它相关的电子增加了不透明度，从而增加了光球层半径。在脉冲衰减阶段，Γ和L0都减小，而rph保持常数或仅微弱变化，这种状况下，L0∝Γ3 (或Μ∝Γ2) [29]。

GRB 131231A的能谱特征行为表明这个暴有一些特殊性，需要寻求合适的理论解释，值得我们进一步深入研究。

参考文献
[1] LI L. Multipulse Fermi Gamma-Ray Bursts. I. Evidence of the transition from fireball to Poynting-flux-dominated outflow[J]. The Astrophysical Journal Supplement Series, 2019, 242(2): 16. DOI: 10.3847/1538-4365/ab1b78
[2] LI L. Thermal components in Gamma-ray Bursts. I. How do they affect non-thermal spectral parameters?[J]. The Astrophysical Journal Supplement Series, 2019, 245(1): 7. DOI: 10.3847/1538-4365/ab42de
[3] ZHANG B B, ZHANG B, LIANG E W, et al. A comprehensive analysis of Fermi Gamma-Ray Burst data. I. Spectral components and their possible physical origins of LAT/GBM GRBs[J]. The Astrophysical Journal, 2011, 730(2): 141. DOI: 10.1088/0004-637X/730/2/141
[4] GUIRIEC S, KOUVELIOTOU C, DAIGNE F, et al. Toward a better understanding of the GRB phenomenon: a new model for GRB prompt emission and its effects on the new LiNT-Epeak, irest, NT relation[J]. The Astrophysical Journal, 2015, 807(2): 148. DOI: 10.1088/0004-637X/807/2/148
[5] NORRIS J P, SHARE G H, MESSINA D C, et al. Spectral evolution of pulse structures in gamma-ray bursts[J]. The Astrophysical Journal, 1986, 301(1): 213–219.
[6] BHAT P N, FISHMAN G J, MEEGAN C A, et al. Spectral evolution of a subclass of Gamma-Ray Bursts observed by BATSE[J]. The Astrophysical Journal, 1994, 426: 604–611. DOI: 10.1086/174097
[7] HAKKILA J, PREECE R D. Unification of pulses in long and short Gamma-Ray Bursts: evidence from pulse properties and their correlations[J]. The Astrophysical Journal, 2011, 740(2): 104. DOI: 10.1088/0004-637X/740/2/104
[8] KARGATIS V E. Continuum spectral evolution of gamma-ray bursts[J]. The Astrophysical Journal, 1994, 422: 260–268. DOI: 10.1086/173724
[9] LI L, GENG J J, MENG Y Z, et al. "Double-tracking" characteristic of the spectral evolution of GRB 131231A: synchrotron origin?[J]. The Astrophysical Journal, 2019, 884(2): 109. DOI: 10.3847/1538-4357/ab40b9
[10] OGANESYAN G, NAVA L, GHIRLANDA G, et al. Characterization of Gamma-Ray Burst prompt emission spectra down to soft X-rays[J]. Astronomy&Astrophysics, 2018, 616: A138.
[11] OGANESYAN G, NAVA L, GHIRLANDA G, et al. Prompt optical emission as a signature of synchrotron radiation in gamma-ray bursts[J]. Astronomy&Astrophysics, 2019, 628: A59.
[12] BAND D L, MATTESON J, FORD L, et al. BATSE observations of gamma-ray burst spectra. I-Spectral diversity[J]. The Astrophysical Journal, 1993, 413(1): 281–292.
[13] AXELSSON M, BALDINI L, BARBIELLINI G, et al. GRB110721A: an extreme peak energy and signatures of the photosphere[J]. The Astrophysical Journal Letters, 2012, 757(2): L31. DOI: 10.1088/2041-8205/757/2/L31
[14] BURGESS J M, GREINER J, BÉGUÉ D, et al. A Bayesian Fermi-GBM short GRB spectral catalogue[J]. Monthly Notices of the Royal Astronomical Society, 2019, 490(1): 927–946. DOI: 10.1093/mnras/stz2589
[15] YU H F, DERELI-BÉGUÉ H, RYDE F. Bayesian time-resolved spectroscopy of GRB pulses[J]. The Astrophysical Journal, 2019, 886(1): 20. DOI: 10.3847/1538-4357/ab488a
[16] LI L, RYDE F, PE'ER A, et al. Bayesian time-resolved spectroscopy of multipulse GRBs: Variations of emission properties among pulses[J]. The Astrophysical Journal Supplement Series, 2021, 254(2): 35. DOI: 10.3847/1538-4365/abee2a
[17] ZHANG B B, ZHANG B, CASTRO-TIRADO A J, et al. Transition from fireball to Poynting-flux-dominated outflow in the three-episode GRB 160625B[J]. Nature Astronomy, 2018, 2(1): 69–75. DOI: 10.1038/s41550-017-0309-8
[18] MEEGAN C, LICHTI G, BHAT P N, et al. The Fermi Gamma-Ray Burst Monitor[J]. The Astrophysical Journal, 2009, 702(1): 791. DOI: 10.1088/0004-637X/702/1/791
[19] GRUBER D, GOLDSTEIN A, AHLEFELD V V, et al. The Fermi GBM Gamma-Ray Burst spectral catalog: four years of data[J]. The Astrophysical Journal Supplement Series, 2014, 211(1): 12. DOI: 10.1088/0067-0049/211/1/12
[20] MICHAEL B J. On spectral evolution and temporal binning in Gamma-Ray Bursts[J]. Monthly Notices of the Royal Astronomical Society, 2014, 445(3): 2589–2598. DOI: 10.1093/mnras/stu1925
[21] SCARGLE J D, NORRIS J P, JACKSON B, et al. Studies in astronomical time series analysis. VI. Bayesian block representations[J]. The Astrophysical Journal, 2013, 764(2): 167. DOI: 10.1088/0004-637X/764/2/167
[22] IYYANI S, RYDE F, AXELSSON M, et al. Variable jet properties in GRB110721A: time resolved observations of the jet photosphere[J]. Monthly Notices of the Royal Astronomical Society, 2013, 433(4): 2739–2748. DOI: 10.1093/mnras/stt863
[23] PREECE R D, BRIGGS M S, MALLOZZI R S, et al. The BATSE Gamma-Ray Burst spectral catalog. I. High time resolution spectroscopy of bright bursts using high energy resolution data[J]. The Astrophysical Journal Supplement Series, 2008, 126(1): 19–36.
[24] FIRMANI C, CABRERA J I, AVILA-REESE V, et al. Time-resolved spectral correlations of long-duration γ-ray bursts[J]. Monthly Notices of the Royal Astronomical Society, 2009, 393(4): 1209–1218. DOI: 10.1111/j.1365-2966.2008.14271.x
[25] GHIRLAN DA G, NAVA L, GHISELLINI G. Spectral-luminosity relation within individual Fermi Gamma Rays bursts[J]. Astronomy&Astrophysics, 2010, 511(2): A43.
[26] PE'ER A, RYDE F, WIJERS R A M J, et al. A new method of determining the initial size and Lorentz factor of Gamma-Ray Burst fireballs using a thermal emission component[J]. The Astrophysical Journal, 2007, 664(1): L1. DOI: 10.1086/520534
[27] RYDE F, PE'ER A. Quasi-blackbody component and radiative efficiency of the prompt emission of gamma-ray bursts[J]. The Astrophysical Journal, 2009, 702(2): 1211. DOI: 10.1088/0004-637X/702/2/1211
[28] RYDE F. Smoothly broken power law spectra of gamma-ray bursts[J]. Astrophysical Letters&Communications, 1998, 39: 281–284.
[29] IYYANI S, RYDE F, BURGESS M J, et al. Synchrotron emission in GRBs observed by Fermi: its limitations and the role of the photosphere[J]. Monthly Notices of the Royal Astronomical Society, 2016, 456(2): 2157–2171. DOI: 10.1093/mnras/stv2751
[30] LUCAS U Z, BING Z, JUDITH R. Toward an understanding of GRB prompt emission mechanism. II. Patterns of peak energy evolution and their connection to spectral lags[J]. The Astrophysical Journal, 2016, 825(2): 97. DOI: 10.3847/0004-637X/825/2/97
[31] KUMAR P, PANAITESCU A. Afterglow emission from naked Gamma-Ray Bursts[J]. The Astrophysical Journal, 2000, 541(2): L51–L54. DOI: 10.1086/312905
[32] UHM Z L, ZHANG B. On the curvature effect of a relativistic spherical shell[J]. Astrophysical Journal, 2015, 808(1): 33. DOI: 10.1088/0004-637X/808/1/33
[33] UHM Z L, ZHANG B. Toward an understanding of GRB prompt emission mechanism. I. The origin of spectral lags[J]. The Astrophysical Journal, 2016, 825(2): 97. DOI: 10.3847/0004-637X/825/2/97
[34] GAO H, ZHANG B. Photosphere emission from a hybrid relativistic outflow with arbitrary dimensionless entropy and magnetization in GRBs[J]. The Astrophysical Journal, 2015, 801(2): 103. DOI: 10.1088/0004-637X/801/2/103
[35] AXELSSON M, ZHANG B B, et al. Identification and properties of the photospheric emission in GRB090902B[J]. The Astrophysical Journal Letters, 2010, 709(2): L172. DOI: 10.1088/2041-8205/709/2/L172
[36] HASCOЁT T R, DAIGNE F, MOCHKOVITCH R. Prompt thermal emission in gamma-ray bursts[J]. Astronomy&Astrophysics, 2013, 551: A124.
[37] METZGER B D. Gamma-ray burst central engines: black hole versus magnetar[C]//Proceedings of the ASP Conference Series. 2010.
由中国科学院国家天文台主办。
0

文章信息

王晨, 彭朝阳, 陈家明
Wang Chen, Peng Zhaoyang, Chen Jiaming
EP和α “双追踪” GRB 131231A的能谱特性研究
Study on Energy Spectrum Characteristics of EP and α "Double Tracking" Gamma-ray Bursts
天文研究与技术, 2022, 19(6): 540-551.
Astronomical Research and Technology, 2022, 19(6): 540-551.
收稿日期: 2022-01-25
修订日期: 2022-02-16

工作空间