2. 贵州师范大学数学科学学院,贵州 贵阳 550001;
3. FAST早期科学数据中心,贵州 贵阳 550001
2. School of Mathematical Science, Guizhou Normal University, Guiyang 550001, China;
3. FAST Early Science Data Center, Guiyang 550001, China
自2016年9月500 m口径球面射电望远镜在我国贵州落成[1]以来,脉冲星搜索一直是重要科学目标之一。截至目前,FAST早期科学数据中心已计算发现了240个新脉冲星候选体[2-5],其中123颗脉冲星候选体已经证实为新脉冲星。J1859-0131和J1931-01是我国射电望远镜首次发现的两颗脉冲星。J0318+0253是FAST发现的首个毫秒脉冲星[3],是至今发现的射电流量最弱的高能毫秒脉冲星之一,展示了FAST对国际低频引力波探测做出实质贡献的潜力,是FAST的重要成果。巡天观测数据经过计算处理[5],产生海量脉冲星候选体诊断图像。以每天处理2 000个数据文件为例,单日产生的图像达到300 000张,存储空间需要20 G。脉冲星候选体诊断图数量呈指数增长,给科学数据管理工作带来挑战。脉冲星候选体诊断图像是科学家对巡天数据进行检查、脉冲星搜索判断的科学数据,是探究新搜索技术方法的数据基础,是天文科研科普开放共享的重要资源。脉冲星识别软件在专用网络中不断传输脉冲星候选体诊断图像,科学家基于脉冲星候选体诊断图像探索新的科研方法,如文[2] 提出的PICS方法。FAST云平台公布的共享信息包含大量的脉冲星候选体诊断图,我们迫切需要研究压缩技术,实现脉冲星候选体诊断图像的有效存储,加快网络传输共享。
传统主流的图像标准算法如JPEG[5],JPEG2000[6]和BPG等采用变换编码。JPEG对图像分块做离散余弦变换(Discrete Cosine Transform, DCT),将图像信息从空域变换到系数能量相对集中的离散余弦变换域,然后量化变换系数和熵编码[3];而JPEG2000对图像做离散小波变换(Discrete Wavelet Transform, DWT),分层熵编码。但离散余弦变换和离散小波变换是固定不变的线性变换函数,近似固定卷积核图像的卷积操作,手工设计的变换矩阵对脉冲星图像数据去相关性不一定最优。近年来基于神经网络学习的图像压缩编码方法[7-10]越来越受到研究者青睐。文[7] 提出基于循环神经网络(Recurrent Neural Network, RNN) 的图像编码框架,文[8] 提出基于卷积神经网络的压缩编码结构,学习网络瓶颈层数据表征的分布熵模型,更好地移除图像的内部冗余。基于神经网络的图像压缩利用大量图像优化学习,在对图像去相关紧凑化压缩变换方面比传统手工设计压缩模块方法更有效。但是,现有的压缩方法都是针对自然图像,没有充分考虑脉冲星诊断图像不同于自然图像的特性。脉冲星诊断图像由稀疏的黑白图像、随机分布的灰度图和彩色图像组成,简单视为彩色图像用一种变换压缩算法处理显然是不合理的。
针对脉冲星候选体诊断图的特征,本文提出使用跳白块编码和深度网络图像压缩模型相结合的压缩方法。针对诊断图像的曲线和文字等黑白图像,首先二值化图像,然后使用改进的自适应分层跳白块算法压缩。对于深度神经网络压缩模型的设计,首先,图像压缩模型采用卷积神经网络自编码器结构,整体结构由正向编码网络、量化器、熵编码器和反向编码网络组成。其次,将量化特征的编码率与失真误差的加权和作为损失函数,利用大量脉冲星候选体诊断图像自适应学习各个模块函数。为了有效利用算术编码器算法对潜在表示特征的分布,算法使用网络学习非线性函数逼近实际的数据分布模型。为了验证提出算法的有效性,实验将近年来FAST巡天项目生成的脉冲星候选体诊断图作为数据集,分别应用JPEG算法、JPEG2000算法、BPG算法和本文提出的深度神经网络压缩模型(Deep Neural Compression Model, DNCM) 算法比较。结果表明,深度神经网络压缩模型算法的峰值信噪比优于JPEG算法,与JPEG2000相当,但结构相似性远远超过传统压缩算法,特别是在低比特率下重构图像较高的结构相似性保证了图像的感官质量。诊断图本是目视判断脉冲星候选体的辅助依据,实验证明本文算法针对脉冲星候选体诊断图压缩应用是有效的。
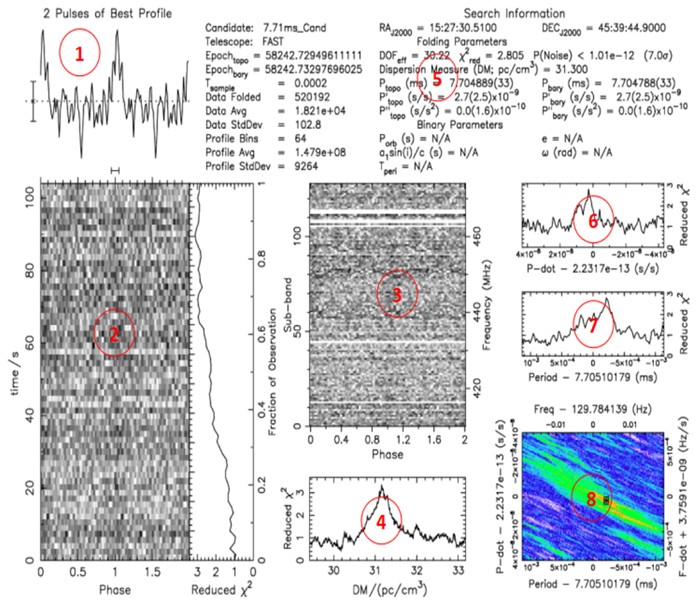
1 分区图像压缩脉冲星候选体诊断图(图 1) 是观测数据经过消色散、周期折叠处理后得到可能的脉冲星旋转参数组合和统计量分布结果数据绘制的图像[1],用于天文学家判定是否为脉冲星。
|
| 图 1 脉冲星候选体诊断图像 Fig. 1 Pulsar candiate diagnostic graph |
诊断图主要包含8个子图,直观上可以粗略分为3类,其中②和③子图为二维灰度散度图,包含大量随机噪声点;①,④,⑤,⑥和⑦为稀疏的曲线图或文字表示的黑白图像;⑧为彩色图像。观察可知,子图特征差异较大,图像通道数量不一,数据稀疏程度差别较大,使用单一的压缩算法或一种压缩模型显然是不合理的。本文将图像区域划分为3类,采用不同方法压缩编码,黑白图像区域使用跳白块编码,灰度图和彩色图分别训练一个深度网络隐变量压缩模型。3类图像区域自动定位切割,并分发到对应编码器压缩处理。
1.1 跳白块编码方法跳白块编码是一种充分利用二值图像中单色区域占大部分位置的特征游程编码变体。一维跳白块编码也称跳白条,将二值图像的各扫描行分成若干块,每块N个像素[11]。全白像素块用1比特字“0”表示,对于至少含有一个黑像素的块,用N+1比特码字表示;含有黑色像素的块第1个比特位表示“1”,称为前缀码,其余N比特直接用自身的二值幅值表示,白为“0”,黑为“1”。推广到二维,将整个图像分割为M × N像素的块,若块为全白像素时用1比特“0”表示;非全白块用1 + M × N个比特码字表示,一个前缀比特“1”,其余MN比特直接用自身的二值幅值表示。将脉冲星候选体图像中的1类区域分割出来,指定阈值变换为二值图像,白像素用“0”表示,黑像素用“1”表示。
如图 2,用跳白块编码二值图像生成二进制数据流,再送入自适应算术编码器(QM编码器),进一步压缩数据流中的位流冗余。本文使用跳白块编码改进的自适应分层跳白块算法。

|
| 图 2 跳白块编码二值图像 Fig. 2 White block skipping coding for binary image |
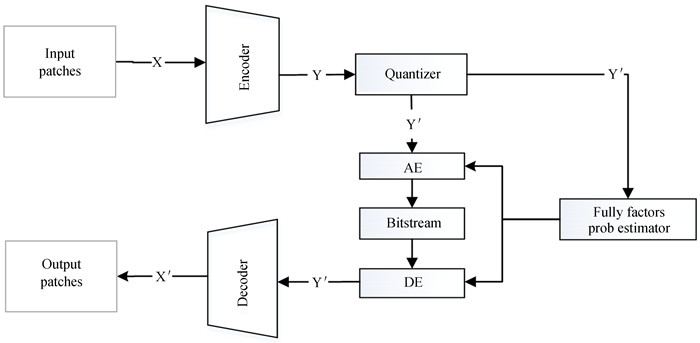
对于灰度图像和彩色图像,本文分别训练两个学习型深度网络隐变量模型压缩相应的图像块。深度网络隐变量压缩模型的整体网络结构是一个自编码器结构,如图 3。压缩网络模型由4部分组成:分析变换网络模块(Encoder)、量化器(Quantizer)、熵编码模块(Entropy Coder)和集成变换网络模块(Decoder)。分析变换网络模块由多个堆叠的卷积层组成,经过一系列下采样、提取特征、去相关等操作,将输入图像映射到弱相关的紧凑的隐变量。潜在表示保留了图像的全部必要信息,是待编码的压缩信息。集成变换网络是分析变换网络的逆操作,也是由一系列堆叠的逆卷积层组成,通过上采样生成图像信息。熵编码模块是依据神经网络学习得到潜在表示分布的参数估计的模型,指导算术编码器将量化器量化后的潜在表示信息生成可以保存和网络传输的二进制码流,即压缩信息。
|
| 图 3 深度神经网络图像压缩模型结构图 Fig. 3 Architecture diagram of deep neural network image compression model |
分析变换器Eϕ(x) 将图像特征数据x映射为潜在表示y,量化器将y量化为
| $ L=D(x, \hat{x})+\beta H(\hat{y}), $ | (1) |
| $ st. H(\hat{y})=-\log _2 p(\hat{y}), D(x, \hat{x})=\|x-\hat{x}\|_2 . $ |
由于压缩编码需要对潜在表示层输出y量化处理,通常使用取整roundΔ操作。本文采用的量化器量化间隔步长为1,用间隔的中心表示量化输出。量化公式为
| $ {\hat{y_i}}=q_i=round\left(y_i\right), $ | (2) |
其中,指示符i贯穿向量的所有元素,包括通道和空间坐标。这样做的好处是
然而,我们分析损失函数(1) 式可以发现,损失函数依赖于量化值,但是取整量化函数的梯度几乎总是0,码率R与失真D组成的损失函数不可微,导致无法使用梯度下降优化损失。为了能够继续使用随机梯度下降优化,在训练过程中,我们加入独立同分布的随机均匀噪声ε,实现抖动的量化器。ε的分布区间和量化器量化间隔的宽度都等于1,在测试和实际编码过程中,我们直接使用取整函数
| $ \hat{y}_i=q_i=\left\{\begin{array}{l} round\left(y_i+\varepsilon\right), \varepsilon \sim u(-0.5, 0.5) \\ round\left(y_i\right), \quad {\rm { when \;testing }} \end{array}\right.. $ | (3) |
图像压缩模型需要对分析变换得到的紧凑的潜在表示信息无损编码,生成二进制码流,本文采用算术编码实现熵编码。算术编码是一种基于信源信息统计的概率分布,将所有编码信息映射到实轴[0, 1) 内小区间表示的最优无损熵编码算法。算术编码的基础是潜在表示分布模型的精准估计,影响码率R和损失D,即压缩器的压缩性能,我们使用一个网络无参数分段线性密度函数模型逼近实际数据的分布。
假定潜在表示空间的数据是独立同分布,则可以建立一个完全因子分解模型,其似然函数为样本的积分,
| $ \begin{aligned} p_\psi\left(\hat{y_i}\right) &=\prod\limits_i p\left[q\left(y_i\right) * u(-0.5, 0.5)\right] \\ &=c\left(\hat{y}_i+0.5\right)-c\left(\hat{y}_i-0.5\right) \end{aligned}, $ | (4) |
其中,c(*) 是先验分布密度模型的累积函数。由(4) 式得到一个以实际数据yi为中心的单位概率质量密度。概率密度模型由潜在表示数据先验分布密度函数卷积一个标准均匀分布密度函数得到,将编码器的输出特征映射作为输入,生成潜在表示特征的概率密度。
本文参考文[9] 设计一个基于深度神经网络的无参数分段线性密度函数模型,通过迭代训练优化实现样本数据与模型之间的拟合。使用卷积网络构建的无参数分段线性密度函数包括K个阶段的非线性变换函数卷积,第K阶段向量映射函数fK: Rm→Rn,其中fK′为密度fK的梯度,是一个雅克比矩阵,可以将模型的累计密度链式计算法则表示为
| $ \begin{aligned} &c=f_K f_{K-1} \cdots f_1, \\ &p=f_K^{\prime} f_{K-1}{ }^{\prime} \cdots f_1^{\prime} . \end{aligned} $ | (5) |
非线性函数具体实现公式为
| $ f_k(x)=g_k\left[H^{(k)} x+b^{(k)}\right] \quad 1 \leqslant k<K, $ | (6) |
| $ f_K(x)={\rm{sigmoid}}\left[H^{(K)} x+b^{(K)}\right], $ | (7) |
| $ g_k(x)=x+a^{(k)} \cdot \tanh (x) . $ | (8) |
其中,fk(x) 表示量化函数前面1 ≤ k<K层变换函数形式;fK(x) 为量化函数最后一层函数形式,使用非线性激活函数σ(·) 将概率分布映射到[0, 1] 区间,即是概率密度的标准分布。
2 实验与结果分析实验将近年来脉冲星搜索巡天的部分结果数据作为图像压缩训练集和测试模型,数据源包括脉冲星图像样本1 159个和射频干扰(Radio Frequency Interference, RFI) 图像样本998个8位无损PNG图像。网络模型在NVIDIA GeForce GTX 1080 GPU上使用Pytorch框架实现。为了验证本文算法的性能,实验随机从测试集中抽取5幅脉冲星图像,测试压缩算法。对黑白图像处理后使用跳白块压缩和PNG压缩结果比较;对灰度图和彩色图区域,将本文的深度压缩算法与JPEG,JPEG2000和BPG算法比较。其中,JPEG采用开源库libjpeg,JPEG2000使用openjpeg实现,BPG使用开源库libbpg。
2.1 跳白块编码过程分割候选体诊断图中1类图像区域,此类图像区域为稀疏的黑白图像,计算像素幅值直方图选定阈值为200,将图像二值化映射为{0, 1};选择跳白块尺寸,经过大量候选体诊断图像压缩试验,选取最优跳白块尺寸大小为5 × 4,获得最优压缩码流;跳白块编码后送入自适应算术编码器。
2.2 深度网络模型结构自编码器的输入与输出尺寸一致,即输入图像的大小通道数与压缩模型重构图像大小一致。本文设计的压缩网络,图像大小256 × 256,分析变换网络模块包括4个卷积层和3个广义的分裂归一化(Generalized Divisive Normalization, GDN) 层,4个ResNet层。卷积层2倍下采样,第1个卷积层用128个9 × 9的卷积核,步长2,填充位4;第2和第3个卷积层有128个5 × 5卷积核,步长为2,填充2。bottleneck层也是卷积层,步长2,填充2,可调节通道数指定16 × 16特征图数量控制码率。集成变换网络模块与分析变换网络模块参数相似,Conv2d替换为ConvTranspose2d,顺序相反。
本文的网络模型基于率失真优化,即压缩损失和码率联合作为目标损失函数,针对灰度图和彩色图训练了两类压缩模型。其中λ为拉格朗日乘子,用于调节不同的压缩损失和码率组合,以满足不同压缩质量要求的场景,即可变码率压缩。实验中,我们训练了10种λ模型,λ取值16, 32, 64, 128, 512, 1 024, 2 048, 4 096, 6 144和8 192,以自适应动量估计算法(Adaptive Moment Estimation, ADAM) 优化模型,初始学习率为10-3,动量因子为0.99,权重衰减率为10-4。迭代优化次数设置为100 000,每次迭代的训练样本批次大小为16。首先训练高码率模型,然后基于这个模型作为预训练模型,分别调整λ值训练其他模型。
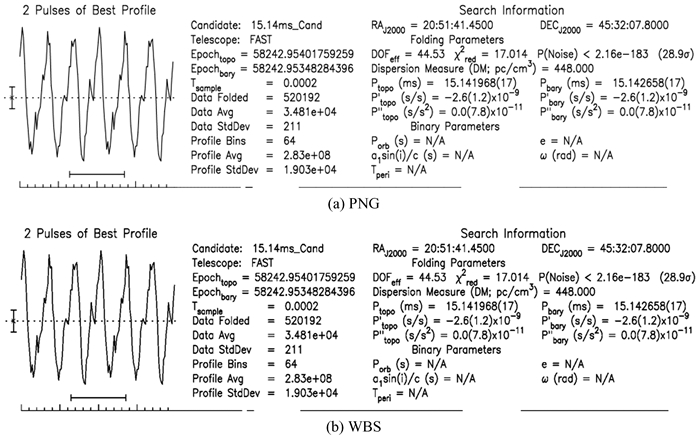
2.3 实验结果与分析 2.3.1 跳白块编码性能评价将候选体诊断图中1类图像区域,用改进的跳白块编码压缩的结果与跳白块编码基本压缩和PNG压缩结果比较,如表 1。黑白图像的PNG和跳白块编码无损压缩结果见图 4。由表 1可以看出,改进的跳白块编码压缩性能是PNG的5倍,加入了QM的跳白块编码压缩性能得到进一步提升。从图 4可以看出,PNG和跳白块编码的黑白图像基本相同,PNG图像边缘更平滑。
| img1 | img2 | img3 | img4 | img5 | ||
| WBS | num of bits | 237 866 | 238 666 | 235 646 | 231 986 | 243 126 |
| bpp | 0.23 | 0.23 | 0.23 | 0.22 | 0.23 | |
| PNG | num of bits | 1 020 392 | 1 079 816 | 1 038 808 | 970 120 | 1 114 472 |
| bpp | 0.98 | 1.03 | 0.99 | 0.93 | 1.07 | |
| NEW WBS | num of bits | 201 548 | 202 144 | 199 230 | 196 092 | 206 869 |
| bpp | 0.193 | 0.194 | 0.191 | 0.188 | 0.198 |
|
| 图 4 黑白图像的PNG和WBS无损压缩结果对比 Fig. 4 Visual comparsion of lossless compression with PNG and WBS |
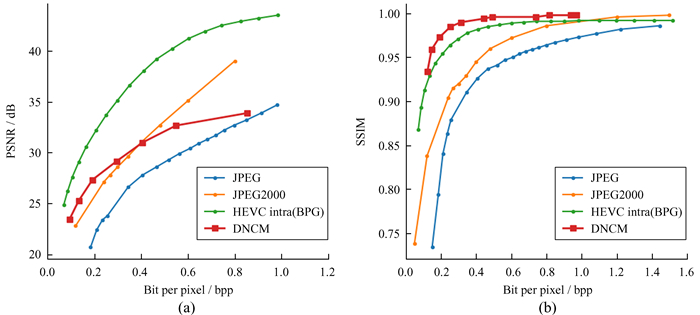
本文设置灰度图像区域和彩色图像的神经网络潜在表示层通道数分别为N=64, 128,下采样倍率为16,训练深度网络压缩模型。由于两类模型方法相同,受篇幅限制,文中仅描述彩色图像网络模型在不同码率下的峰值信噪比和结构相似性。图 5 (a)为峰值信噪比-码率曲线,反映各种算法在不同码率下解码图像与原图像像素之间的均方误差。整体上,深度网络压缩模型算法性能与JPEG2000相近,明显优于JPEG算法,但不及BPG算法。在bpp为0.4时,深度网络压缩模型的峰值信噪比为31 dB,与JPEG2000算法交叉,比JPEG算法高1.4 dB,比BPG算法低8 dB。压缩效果明显优于JPEG和JPEG2000算法,接近BPG算法。接近无损压缩时,传统压缩算法超出神经网络方法,这是卷积神经网络的过平滑造成的。图 5 (b)为结构相似性-码率曲线,反映各种算法在不同码率下解码图像与原图像结构相似度。深度神经网络压缩模型算法的结构相似性明显高于JPEG算法和JPEG2000算法,略高于BPG算法。在bpp为0.2时,深度神经网络压缩模型算法的结构相似性高于0.99,BPG算法的结构相似性为0.95,而bpp < 0.7时,深度神经网络压缩模型算法的结构相似性依然高于0.95,说明在较低比特率高压缩比情况下,深度神经网络压缩模型算法在保持图像感知质量上有绝对优势。
|
| 图 5 图像压缩峰值信噪比和结构相似性率失真曲线比较 Fig. 5 Rate-distortion curves of image compression using PSNR and SSIM metric |
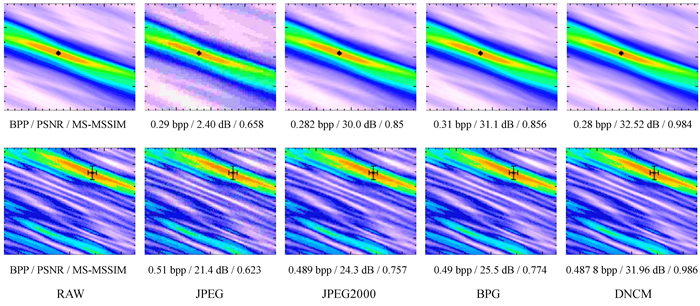
图 6展示了不同的图像压缩算法在相近码率的视觉结果。由图 6可以看出,JPEG算法出现块效应,深度神经网络压缩模型算法多数情况下与BPG算法性能相近,比JPEG算法和JPEG2000算法效果好,图中两幅诊断图的彩色图在相对小的码率下取得最好的视觉质量。
|
| 图 6 可视化结果比较JPEG, JPEG2000, BPG和DNCM的质量 Fig. 6 Visual comparsion among JPEG, JPEG2000, BPG, and DNCM original image |
总之,脉冲星诊断图包含大量稀疏曲线、随机噪声点灰度图和彩色图像块,任何一种传统的有损压缩算法都不是最优选择,本文根据分区策略,利用跳白块编码和神经网络压缩模型对诊断图像压缩具有针对性和专用性。曲线文字图像块转化为二值图像后跳白块压缩几乎没有损失,却得到极高的压缩比,特别是网络压缩模块的功能函数是利用大量的诊断图学习得到,最大程度地反映了诊断图像数据的空间特征,进一步反映得到模型的专用性。脉冲星诊断图最重要的作用是辅助人类目视判断脉冲星候选体,识图时观测的重点是曲线图像和子图图像的结构信息,本文提出算法在低比特率下保持较高的结构相似性,反映了视觉感知质量的优势。
3 总结脉冲星诊断图像由稀疏的黑白图像、随机分布的灰度图和彩色图像组成,简单视为彩色图像, 用一种变换压缩算法处理显然是不合理的。为此,本文提出跳白块编码和深度网络压缩方法对诊断图像分区压缩。跳白块编码针对单色区域占大部分的二值图像具有较好的压缩效果,提取脉冲星诊断图中的曲线子图和文字描述子图,选定量化阈值,将图像二值化为比特位矩阵表示的图像,选取最优跳白块尺寸,实现跳白块编码后送入自适应算术编码器进一步提升压缩性能,最终压缩比是PNG的5倍。基于深度网络压缩方法对灰度图和彩色图分别训练模型,深度网络压缩模型是由卷积神经网络实现的自编码器结构,由分析变换编码网络、量化器、熵编码器和合成变换编码网络组成。各个压缩模块均由学习方法利用大量脉冲星候选体诊断图像优化,变换映射能力比传统手工设计模块更有效,图像经过分析变换映射为潜在表示,是去相关的更紧凑的图像信息。学习的熵编码模块是对潜在表示空间分布的拟合逼近,是比累积概率直方图更精准、更容易操作的概率模型,指导基于统计分布的算术编码器无损编码。实验结果表明,本文提出的深度网络压缩算法对近年来FAST巡天搜索项目脉冲星候选体诊断图的压缩性能,峰值信噪比优于JPEG算法,与JPEG2000相当,而结构相似性远超过传统压缩算法。本文充分利用子图间特征的显著差异,制定分区压缩策略将图像分成3类区域,根据子图图像特征分别使用跳白块编码和深度神经网络压缩方法,提高了编码效率。本文利用神经网络实现的熵估计模型是十分简洁易操作的方式,估计的熵模型是否能够精准有效地匹配真实的潜在分布直接影响损失和码率,因此,新方法提高熵模型的精准估计可以进一步改善压缩性能。
| [1] | XU Y Y, LI D, LIU Z J, et al. Application of aritificial intelligence in the selection of plusar candidate[J]. Progress in Astronomy, 2017, 35(3): 304–315. |
| [2] | ZHU W W, BERNDSEN A, MADSEN E C, et al. Searching for pulsars using image pattern recognition[J]. The Astrophysical Journal, 2014, 781(2): 117. DOI: 10.1088/0004-637X/781/2/117 |
| [3] | QIAN L, PAN Z C, LI D, et al. The first pulsar discovered by FAST[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2019, 62(5): 71–74. |
| [4] | YU Q, PAN Z, QIAN L, et al. A PRESTO-based parallel pulsar search pipeline used for FAST drift scan data[J]. Research in Astronomy and Astrophysics, 2020, 20(6): 215–222. |
| [5] | LI X M, WAN L Q, ZHOU Y J. The application of MATLAB based DCT in JPEG image compression[J]. Electronics Optics & Control, 2005, 12(2): 64–67. |
| [6] | LIU F M, WU Y H, YU J X. Image compression process and principle of JPEG2000[J]. Journal of Computer-Aided Design & Computer Graphics, 2002, 10(14): 905–911. |
| [7] | TODERICI G, OMALLEY S M, HWANG S J, et al. Variable rate image compression with recurrent neural networks[C]//Proceedings of the 4th International Conference on Learning Representations. 2016. |
| [8] | BALLE J, LAPARRA V, SIMONCELLI E P. End-to-end optimized image compression[C]//Proceedings of the 5th International Conference on Learning Representations. 2017. |
| [9] | THEIS L, SHI W Z, Andrew C, et al. Lossy image compression with compressive autoencoders[C]//Proceedings of the 5th International Conference on Learning Representations. 2017. |
| [10] | MINNEN D, BALLÉ J, TODERICI G. Joint autoregressive and hierarchieal priors for learned image compression[J]. Advances in Neural Information Processing System, 2018, 1: 10771–10780. |
| [11] | LIU Y, YIN L X, ZHAO Y. New adaptive block skipping coding of binary image[J]. Computer Engineering, 2009, 35(13): 219–221. |



