2. 中国科学院射电天文重点实验室,江苏 南京 210033;
3. 新疆射电天体物理重点实验室,新疆 乌鲁木齐 830011;
4. 新疆大学物理科学与技术学院,新疆 乌鲁木齐 830046
2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
3. Key Laboratory of Xinjiang Radio Astrophysics, Urumqi, 830011, China;
4. School of Physics and Technology, Xinjiang University, Urumqi 830046, China
中国科学院新疆天文台南山25 m射电望远镜(NanShan Radio Telescope, NSRT) 始建于1993年,是方位- 俯仰轮轨式赋型卡赛格林天线。望远镜于2015年完成系统性升级改造,观测频段提高至43 GHz,观测频段的提高给天线指向精度和面型精度带来了新的挑战。根据实际测量的指向,天线指向误差在白天最高可达20~30″。初步分析认为,这部分指向误差的主要来源是太阳辐照引起的座架非均匀温度,以及由此产生的热致座架结构形变,严重限制了望远镜用于高频观测的时间。南山25 m射电望远镜面临的热致误差问题对于中高频射电望远镜并不鲜见,随着现代全可动射电望远镜向大口径方向发展[1],太阳辐照引起的天线非均匀温度场及结构热致变形问题引起了众多国内外天文领域工程师和研究人员的关注[2-10]。相关研究难点集中在天线热力学特性和热致变形的分析方法上,部分研究在天线结构关键位置处布设少量传感器,通过回归分析等数据分析方法建立天线误差和温度测量数据的经验模型。部分学者通过有限元热分析直接根据天线热环境参数仿真获取天线结构温度场。但热力学有限元分析中影响仿真结果准确程度的敏感参数众多,需要把握天线热力学环境对天线温度场分布产生主要作用的关键因素,着重处理计算精度、建模细节与计算效率三者之间的矛盾。由于射电望远镜热环境以及工作情况的复杂性,单纯的热力学分析方法的准确度有待提高。综合国内外研究现状来看,通过在天线结构关键位置上布设少量温度传感器,并利用测量数据对天线温度场热力学分析模型进行修正,是有希望解决如何准确获取天线结构全局温度场这一难题较为可行的方法。
前期项目组进行了温度场仿真和实测[10],但在仿真中未考虑阴影遮挡对结构温度分布产生的影响。本文针对天线昼间指向误差增大问题,首先在25 m天线座架上布设若干温度传感器和一台太阳辐射传感器,对座架关键点温度和太阳辐射参数进行测量,并基于测量数据建立对25 m天线座架进行热力学建模和多工况下结构温度场仿真,计算了部分工况下天线座架由非均匀温度产生的倾斜情况,并分析产生热变形的原因。
1 天线座架温度特性分析射电望远镜在跟踪观测模式时,其俯仰角和方位角随着射电源位置缓慢变化,由于射电源的运动规律与太阳光线运动规律一致,天线在此工况下相对太阳的姿态在短时间内不会发生大幅度变化,一般来说气温、云量、风速等热环境参数在短时间内是稳定的,天线结构在一个较短时间周期内处于准稳态热力学状态。观测时间较长或射电望远镜切换观测源使天线相对太阳的姿态角发生较大的变化时,天线结构热力学输入随之产生较大变化,此时天线温度场分析属于瞬态热力学问题,可以建立瞬态热力学方程并求解天线结构的温度场。
1.1 天线热环境模型对具体的天线座架结构而言,单元热输入由以下几部分构成[11]。
(1) 总辐射热量qr
太阳总辐射热量是天线结构表面热量最主要的来源,对于处在露天环境下的天线结构,受到的热辐射主要有太阳直射、地面反射和天空散射。
太阳直射辐射强度由
| $ G_{\mathrm{d}}=A C_{\mathrm{N}} {\mathrm{e}}^{-B / \sin \beta} \cos \theta $ | (1) |
计算,其中,A为太阳辐射常数;B为大气消光系数;CN为大气清洁因子;β为太阳高度角;θ为太阳入射方向与物体表面的夹角。
地面反射辐射强度由
| $ G_{\mathrm{r}}=0.5 \rho_{\mathrm{g}}(1+\cos \alpha)(C+\sin \beta) G_{\mathrm{d}} / \cos \theta $ | (2) |
计算,其中,α为物体表面与水平面的夹角;ρg为地面反射系数,根据天线周围地面覆盖类型取值,碎石路面可以取0.3~0.4;C为大气散射因子,晴朗干燥天气可以取0.13。
天空背景辐射强度由
| $ G_{\mathrm{s}}=0.5 C(1+\cos \alpha) G_{\mathrm{d}} \cos \theta $ | (3) |
计算。物体表面接收的总辐射功率为
| $ G_{\mathrm{T}}=\gamma\left(G_{\mathrm{d}}+G_{\mathrm{s}}+G_{\mathrm{r}}\right), $ | (4) |
其中,物体表面吸收率γ根据天线结构件材料表面处理工艺取值,天线使用富锌底白色醇酸漆,吸收率可以取0.2。
太阳辐射热量为
| $ q_{\mathrm{r}}=\iint G_{\mathrm{T}} {\mathrm{d}} t {\mathrm{~d}} S $ | (5) |
(2) 对流交换热量qc
南山25 m射电望远镜为无天线罩和主动热控手段的天线, 天线结构处于自由对流换热环境。处于空气中物体的自由对流换热系数与风速、物体表面形状、物体表面与空气温差等因素有关。为降低计算模型的复杂程度, 自由对流换热系数由
| $ h_{\mathrm{c}}=4.0 v+5.6 $ | (6) |
计算,其中,v为风速,单位为m/s,可通过风速风向传感器实测获得。
对流换热量为
| $ q_{\mathrm{c}}=\iint h_{\mathrm{c}} {\mathrm{d}} t {\mathrm{~d}} S . $ | (7) |
(3) 热边界条件与初始条件
边界条件定义为天线滚轮在与轨道接触的4个节点处等于大地温度,大地温度定义为
| $ T_{\mathrm{g}}=T_{\mathrm{a}}+\Delta T_{\mathrm{g}}, $ | (8) |
其中,Ta为气温;ΔTg在白天取5~10 ℃,夜间取-10~-5 ℃。
初始条件设置为凌晨00: 00时结构温度均匀,等于此时的气温。
1.2 天线座架结构模型天线座架为桁架式结构,所有梁采用工字梁截面,座架构成包括轨道、A型架、一次平台框架、二次平台框架、俯仰轴平台以及辅助框架。天线结构力学和热参数如表 1。
| Material | Density /(kg·m-3) | Young′s modulus /Gpa | Poisson′s ratio | Thermal conductivity /(m·K) | Coefficient of thermal expansion | Specific heat capacity /(J·kg-1·℃-1) | Reference temperature /℃ |
| 16Mn | 7 870 | 212 | 0.31 | 52 | 12.8×10-6 | 480 | 10 |
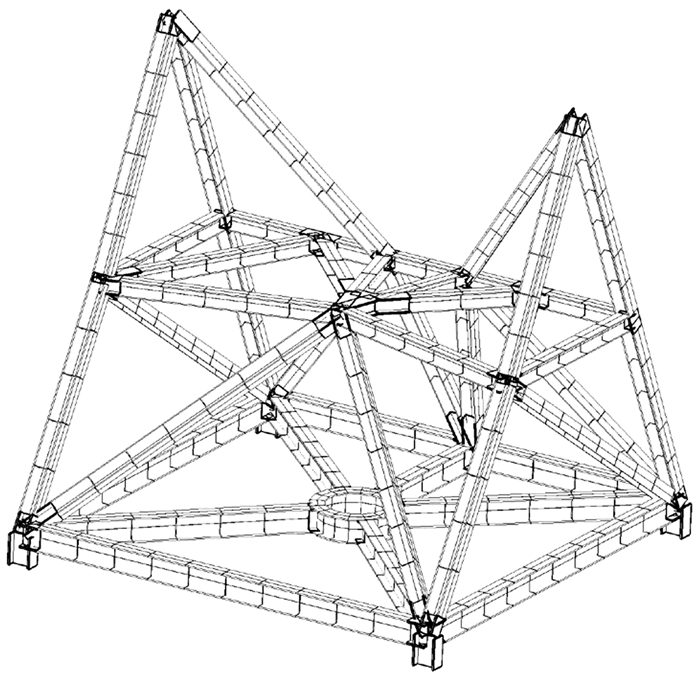
由于面单元能更好地反映座架间的遮挡情况,并体现截面间的温度梯度,本文采用面单元对座架进行建模,并在结构链接处采取等效热单元对连接处进行简化。天线座架有限元模型结构如图 1。
|
| 图 1 天线座架有限元模型结构图 Fig. 1 FEM of antenna alidade |
通过有限元方法对连续的天线结构进行单元划分离散化,对于天线结构上的任意单元应满足单元瞬态热平衡方程
| $ c_{\mathrm{e}} \dot{t}+k_{\mathrm{e}}(t) t=q_{\mathrm{e}}(t), $ | (9) |
其中,
| $ {\boldsymbol{C}}({\boldsymbol{T}}) \dot{{\boldsymbol{T}}}+{\boldsymbol{K}}({\boldsymbol{T}}) {\boldsymbol{T}}={\boldsymbol{Q}}({\boldsymbol{T}}), $ | (10) |
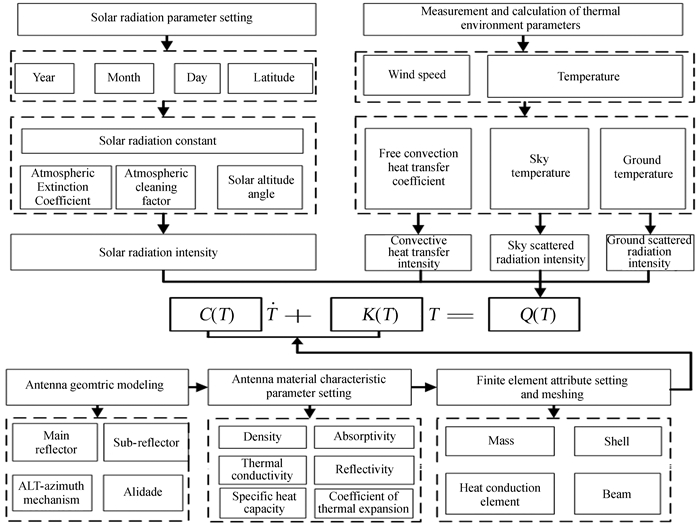
其中,T为天线结构温度列阵;C为热容矩阵;K为热传导矩阵;Q为热输入矩阵。本文建立矩阵形式的瞬态热力学方程。建模流程如图 2。首先按(1)~(7) 式分析太阳辐照等结构热量输入,按(8) 式设定边界条件和初始条件,并建立天线座架几何结构模型和网格参数,即可建立天线座架结构瞬态热平衡方程(10) 式,利用有限元平台可实现该方程的求解,得到对应状态下的座架结构温度分布。
|
| 图 2 建模流程图 Fig. 2 Modeling flowchart |
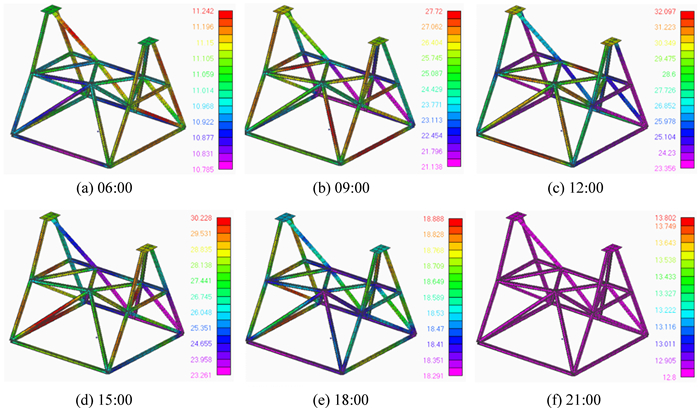
为了研究天线座架温度场情况,本文以2021年4月26日的实际热流条件为输入,求解(10) 式,获取天线座架温度场在一天内的变化,如图 3。
|
| 图 3 天线座架温度分布云图 Fig. 3 The contour of temperature distribution on antenna alidade |
在天线座架上布设单点温度测量系统,可以验证和校正天线座架温度仿真精度。首先需针对天线座架结构和温度特性,对传感器进行布局设计。
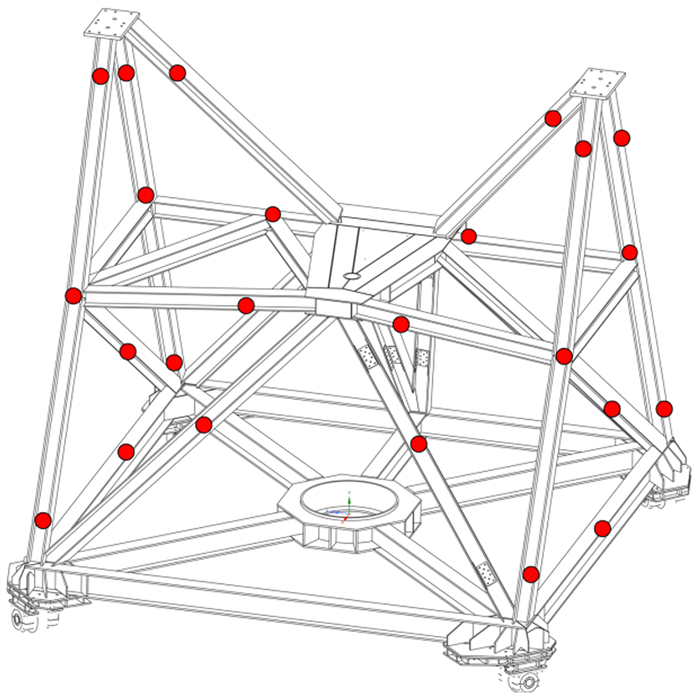
2.1 天线座架温度传感器布局从第1.4节天线温度特性仿真分析结果可知,天线座架在多种可能出现的极端工况下的结构平均温度梯度为0.25 ℃/m,考虑光纤光栅传感器在-20~60 ℃下测温精度为0.5 ℃,传感器的平均间隔2 m为宜,按此间距布设传感器可以充分利用传感器现有精度对天线座架结构温度分布进行还原,同时最大程度上精简传感器数量。综合上述考虑和分析,我们共布设24个传感器,位置和间距布局如图 4。
|
| 图 4 温度传感器布局 Fig. 4 The layouts for temperature sensors |
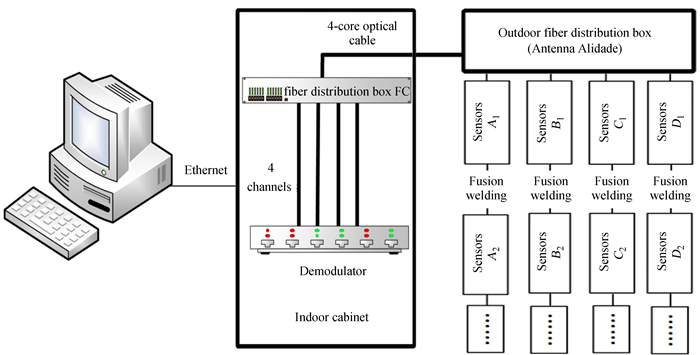
本文采取光纤光栅温度传感器对结构进行测温,测量系统主要由计算机、光纤光栅解调仪、光缆、分纤箱、光纤皮线以及光纤光栅温度传感器构成(如图 5)。相较于传统的接触式测温传感器,如热电偶式PT100温度传感器和电子芯片式DS18B20传感器,光纤光栅温度传感器有以下优点:(1) 对射电望远镜无电磁干扰问题;(2) 传感器分辨率高;(3) 可采取串联式的接线方式,布线简单。系统接线图如图 6。

|
| 图 5 光纤光栅温度传感器 Fig. 5 Fiber grating temperature sensor |
|
| 图 6 温度测量系统接线图 Fig. 6 A wiring diagram for the temperature measurement system |
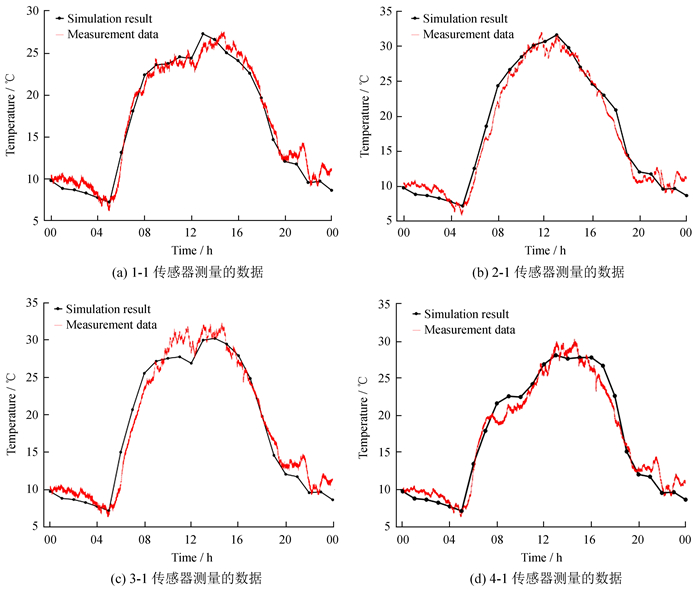
通过温度传感器实测所得天线座架上部分位置的温度在一天内的变化曲线如图 7。图中红色实线为传感器测量数据,黑色点折线为通过第1节所述仿真方法获取的仿真数据,两者相对精度优于85%。从图 7可以看出,仿真方法能够较为准确地反映天线座架的温度分布特点。
|
| 图 7 传感器实测天线座架温度随时间变化曲线 Fig. 7 Temperature data measured by sensors |
天线座架结构温度的非均匀分布会使天线结构产生热变形。以往研究中的热变形需利用热分析工具计算天线温度场,然后作为载荷映射至结构分析有限元模型,从而计算结构温度场,此过程需要较长的计算时间。本文通过分析天线座架变形规律,建立有限元节点位移至天线轴系误差的矩阵式关系,有效节省计算时间。
3.1 天线座架变形参数分析天线热致轴系误差的快速计算,需要推导建立有限元位移场与天线轴系误差间的几何关系。天线热致轴系误差示意图如图 8,其中,Of为固定坐标系;y轴与天线座架俯仰轴方向平行;z轴垂直于水平基准面;A点和B点为俯仰轴端点,AB为俯仰轴;O为将Of原点平移至A点的坐标原点;A′和B′为热致变形后的A点、B点,A′B′为热变形后的方位轴。平移A′B′,使A′点与A点重合,此时B′平移至B″;Bp为B′点在x-O-y平面的投影,α为ABp与AB的夹角,β为ABp与A″B″的夹角。

|
| 图 8 天线俯仰轴热致轴系误差示意图 Fig. 8 A schematic on thermally induced shaft deformation of the alidade |
在Of坐标系中,记A点坐标为(Xa, Ya, Za),B点坐标为(Xb, Yb, Zb),A′点坐标为(X′a, Y′a, Z′a),B′点坐标为(X′b, Y′b, Z′b),记X′ab=X′b - X′a,Y′ab=Y′b - Y′a,Z′ab=Z′b - Z′a,向量AB =(X′ab, Y′ab, Z′ab)。
在O坐标系中,A点坐标为(0, 0, 0),B点坐标为(Xb - Xa, Yb - Ya, Zb - Za),A′点坐标为(X′a - Xa, Y′a - Ya, Z′a - Za),B′点坐标为(X′b - Xa, Y′b - Ya, Z′b - Za),B″点坐标为(Xb + ubx - (Xa + uax), Yb + uby - (Ya + uay), Zb + ubz - (Za + uaz))=(Xb - Xa + ubx - uax, Yb - Ya + uby - uay, Zb - Za + ubz - uaz),Bp点坐标为(X′b - X′a, Y′b - Y′a, 0)。α和β可由
| $ \tan \alpha=\frac{X_b^{\prime}-X_a^{\prime}}{Y_b^{\prime}-Y_a^{\prime}}=\frac{X_b-X_a+u_b^x-u_a^x}{Y_b-Y_a+u_b^y-u_a^y}, $ | (11) |
| $ \begin{aligned} \sin \beta &=\frac{Z_b^{\prime}-Z_a^{\prime}}{\sqrt{\left[X_b^{\prime}-X_a^{\prime}\right]^2+\left[Y_b^{\prime}-Y_a^{\prime}\right]^2+\left[Z_b^{\prime}-Z_a^{\prime}\right]^2}} \\ &=\frac{Z_b-Z_a+u_b^z-u_a^z}{\sqrt{\left[X_b-X_a+u_b^x-u_a^x\right]^2+\left[Y_b-Y_a+u_b^y-u_a^y\right]^2\left[Z_b-Z_a+u_b^z-u_a^z\right]^2}} \end{aligned} $ | (12) |
计算。因为热致变形为线弹性、小变形,α和β都是小量,可以认为tanα≈α,sinβ≈β,即以(11) 式和(12) 式作为热致座架结构偏移计算标准。
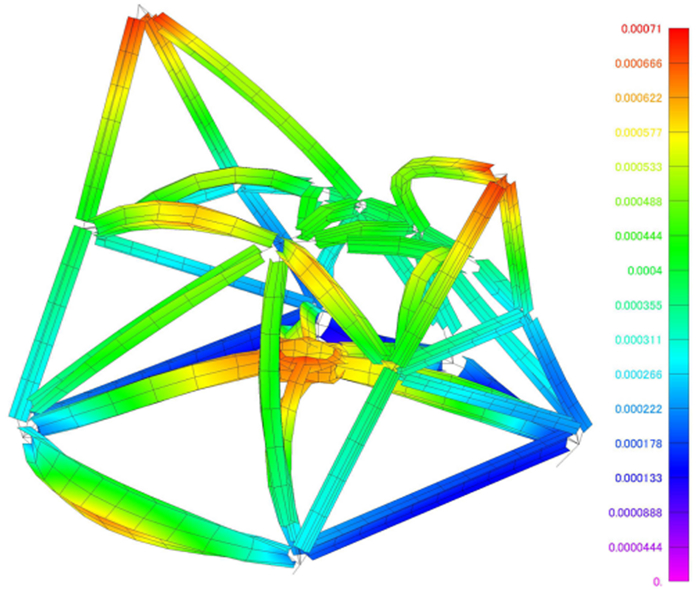
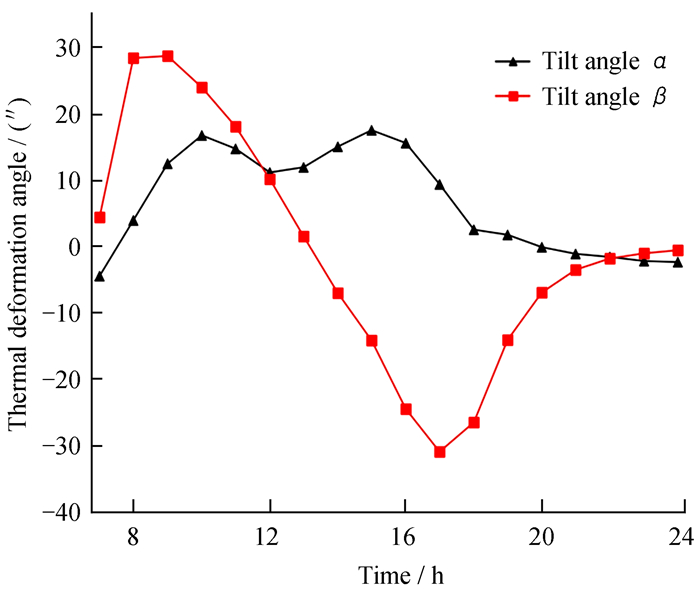
3.2 天线座架热变形仿真仿真日期设置为2021年4月26日,当日天气晴朗无风,将仿真所得温度场输入天线结构有限元模型,实现天线座架结构温度变形的快速计算。图 9为天线实测温度输入时仿真所得热变形云图(变形经过放大),图中变形单位为m。图 10为7时至24时α和β随时间的变化情况。
|
| 图 9 天线座架热变形云图 Fig. 9 The contour of thermal deformation of an antenna alidade |
|
| 图 10 7时至24时α和β随时间的变化情况 Fig. 10 Changing of the angle α and β over time from 7AM to 12PM |
倾角α代表座架绕y方向的偏差,倾角β代表座架绕x方向的偏差,两者在不同方向影响天线的指向精度。从图 10可以看出,由于座架朝向正南方向,当太阳从东方升起时,首先辐照到座架东侧,此时天线座架东西两侧的温度差值升高,天线座架产生绕x轴的热致偏移。随着太阳辐照逐渐向西偏移,两侧温差逐渐减小,而后又逐渐增大,直至20时后太阳逐渐落下,因此可以判定座架绕x轴的旋转角β随着天线座架东西侧温差有明显的规律性偏移。α曲线也有类似情况,随着太阳升起A型架南北两侧温差逐渐增大,但有所不同的是在太阳角升到一定高度,太阳光线能够同时辐照到座架南北两侧,因此南北两侧温差在正午时反而降低,此即图中α曲线在正午时刻反而“凹陷”的原因。综合来看,座架前后、左右温差与其两方向的热致偏移呈强相关,这与70 m口径射电望远镜天线座架[12]表现的特性一致。
4 结束语本文通过建立射电望远镜天线座架热力学分析模型和天线热环境模型,对不同太阳辐照工况下的天线座架温度分布以及随时间的变化进行了仿真,并通过在25 m天线座架上布设24个温度传感器,对座架的温度分布差异进行了测量。测量数据显示,本文建立的天线座架热力学模型拥有较为准确的仿真精度。同时,通过将实测温度数据映射至天线结构分析模型,建立天线结构位移场至天线座架轴系偏差间的数学模型,对不同工况下天线座架轴系偏差进行了计算,结果显示,天线座架轴系偏差与座架南北、东西两侧的温度偏差存在明显的联系。
| [1] |
王娜. 新疆奇台110米射电望远镜[J]. 中国科学: 物理学力学天文学, 2014, 44(8): 783–794 WANG N. Xinjiang Qitai 110 m radio telescope[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2014, 44(8): 783–794. |
| [2] | GREVE A, BREMER M. Thermal design and thermal behaviour of radio telescopes and their enclosures[M]. Berlin: Springer, 2010. |
| [3] | BREMER M, GREVE A, ANDERSEN T, et al. A dynamic thermal model for design and control of an 800-element open-air radio telescope[C]//Proceedings of SPIE. 2011. |
| [4] |
王从思, 刘鑫, 王伟, 等. 大型反射面天线温度分布规律及变形影响分析[J]. 宇航学报, 2013, 34(11): 1523–1528 WANG C, LIU X, WANG W, et al. Analysis method for temperature distribution characteristic and thermal distortion of large reflector antennas[J]. Journal of Astronautics, 2013, 34(11): 1523–1528. |
| [5] |
钱宏亮, 钟杰, 范峰. 上海65 m射电望远镜天线结构日照非均匀温度场[J]. 土木工程学报, 2014, 47(3): 39–46 QIAN H L, ZHONG J, FAN F. Analysis on non-uniform temperature field due to sunshine for the antenna structure of Shanghai 65-meter-aperture radio telescope[J]. China Civil Engineering Journal, 2014, 47(3): 39–46. |
| [6] |
常文文, 艾力玉苏甫, 许谦, 等. 基于有限元方法的25 m天线座架结构热特性分析[J]. 机械科学与技术, 2015, 34(5): 812–816 CHANG W W, AILI Y S P, XU Q, et al. Thermal characteristics analysis of 25 m antenna mounts based on the finite element method[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(5): 812–816. |
| [7] |
连培园, 朱敏波, 王伟, 等. 一种轴对称反射面天线温度场实时预估方法[J]. 机械工程学报, 2015, 51(6): 165–172 LIAN P Y, ZHU M B, WANG W, et al. Estimation method of temperature field of large axial symmetric reflector antenna in real-time[J]. Journal of Mechanical Engineering, 2015, 51(6): 165–172. |
| [8] | QIAN H, CHEN D, FAN F, et al. Evaluation of solar temperature field under different wind speeds for Shanghai 65 m radio telescope[J]. International Journal of Steel Structures, 2016, 16(2): 383–393. DOI: 10.1007/s13296-016-6011-3 |
| [9] | PRESTAGE R, CONSTANTIKES K T, BALSER D S, et al. The GBT precision telescope control system[C]//Proceedings of SPIE. 2004. |
| [10] |
王惠, 宁云炜, 闫浩. 26米天线座架温度分布规律及变形影响分析[J]. 天文研究与技术, 2018, 15(2): 208–215 WANG H, NING Y W, YAN H. Temperature distribution and deformation impact analysis of 26 m antenna frame[J]. Astronomical Research & Technology, 2018, 15(2): 208–215. DOI: 10.14005/j.cnki.issn1672-7673.20171108.001 |
| [11] | DUFFIE J A, BECKMAN W A. Solar engineering of thermal processes[M]. 4th ed. New Jersey: John Wiley & Sons Incorporation, 2013: 68-71. |
| [12] | WEI S, KONG D, WANG Q. Effect of the alidade thermal behavior on the pointing accuracy of a large radio telescope[J]. Research in Astronomy and Astrophysics, 2021, 21(6): 125–134. |



