2. 中国科学院云南天文台,云南 昆明 650216
2. Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, China
脉冲星是一种快速旋转、高磁化的中子星,是理解超密度物质的关键,可以用于各种基础物理实验[1]。目前,脉冲星搜索方法主要分为周期性搜索和单脉冲搜索两大类。其中,周期性搜索通过应用快速傅里叶变换(Fast Fourier Transform, FFT) 将时间序列转化到频域,以识别周期性信号,然后在确定的周期内对原始时间序列数据进行折叠,以提高周期性信号的信噪比[2]。而单脉冲搜索寻找强的、非周期的脉冲,并未使用快速傅里叶变换和折叠。单脉冲搜索非常适合发现周期性搜索中无法发现的孤立爆发。研究人员应用单脉冲搜索发现了旋转射电暂现源(Rotating Radio Transients, RRAT)[3]和快速射电暴的(Fast Radio Bursts, FRB)[4]。
2003年,文[5]首次提出了一个理论框架,运用单脉冲搜索方法探测射电天文观测数据中的脉冲星信号。2009年,文[6]把单脉冲搜索应用于阿雷西博L波段馈源阵列脉冲星巡天(Pulsar Arecibo L-band Feed Array, PALFA) 七波束观测数据,发现了7颗脉冲星。2010年,文[7]使用单脉冲搜索方法对帕克斯多波束脉冲星巡天(Parkes Multibeam Pulsar Survey, PMPS) 数据进行重新分析,发现10颗旋转射电暂现源。2015年,文[8]在单脉冲理论的基础上,设计针对旋转射电暂现源的搜索工具RRATtrap,应用在绿岸射电望远镜(Green Bank Telescope, GBT) 350 MHz观测数据,最终探测到18颗旋转射电暂现源。2016年,文[9]首次将单脉冲搜索与机器学习相结合,提出递归峰值识别算法(Recursive Algorithm for Peak IDentification, RAPID),实现了自动化筛选脉冲星候选体,并探测到6颗脉冲星。
2016年9月, 位于贵州喀斯特山区的500 m口径球面射电望远镜进入科学运行阶段,望远镜先后配置了超宽带接收机和L波段19波束接收机[10]。为充分利用FAST优异的探测能力,2018年,文[11]设计并实施了FAST多科学目标同时扫描巡天,即同时使用多个数字终端采集脉冲星、中子氢、分子谱线、旋转射电暂现源、快速射电暴等多个科学目标的观测数据。鉴于单脉冲搜索方法在各大射电望远镜的成功应用,本文对CRAFTS超宽带数据文件的单脉冲搜索结果进行研究,发现CRAFTS单脉冲搜索筛选得到脉冲星候选体存在数以万计的假阳性样本。因此,我们根据脉冲星信号在色散量信噪比曲线大致是高斯曲线以及信噪比数据分布是高斯分布的假设,构造3个显著区分脉冲星信号和干扰的特征,旨在缓解出现大量假阳性样本的问题。试验结果表明,添加特征值判断的单脉冲筛选工具与传统方法相比,假阳性样本数量减少了20%。
1 CRAFTS超宽带数据单脉冲搜索实验在射电天文观测数据中发现脉冲星通常分为4个阶段:收集、消色散、周期性搜索或单脉冲搜索和人工检查[1]。第1阶段,原始数据以电压时间序列的形式由射电望远镜收集;第2阶段,脉冲辐射通过星际介质(Interstellar Medium, ISM) 的色散效应,导致较低频率的脉冲比较高频率晚到达[12],消色散可以去除这些与频率有关的延迟效应的影响;第3阶段,使用周期性搜索或单脉冲搜索找出脉冲星候选体;第4阶段,对判断为脉冲星候选体的数据进行人工检查。
我们先使用PRESTO (Pulsar Exploration and Search Toolkit) 脉冲星搜索工具处理2017年8月至2018年5月CRAFTS的超宽带数据,处理流程包括去干扰、消色散和单脉冲搜索等步骤;然后,应用单脉冲筛选工具RRATtrap从PRESTO的Single_pulse_search.py输出文件中筛选出脉冲星候选体。
单脉冲筛选工具RRATtrap根据脉冲星信号的特性区分脉冲星信号和干扰。(1)脉冲星信号出现在一定色散量(Dispersion Measure, DM) 范围内,在最佳色散量时检测到峰值信噪比,而在该色散量上下信噪比下降,这是由于脉冲以不准确的色散量消色散时导致脉冲展宽造成的。(2) 由于信号在最佳色散量检测到峰值信噪比,预计来自地面的信号(即射频干扰) 在色散量为0 pc·cm-3时达到峰值。同时射频干扰(Radio Frequency Interference, RFI) 不受色散效应的影响,因此,脉冲星信号出现在一个非常大的色散量范围内[8]。
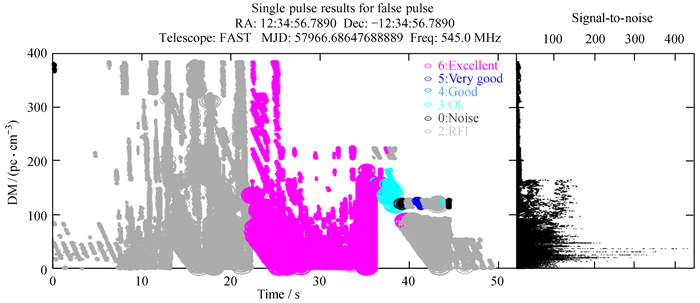
图 1是单脉冲筛选工具RRATtrap探测到已知脉冲星PSR B0540+23的诊断图。左侧子图纵坐标为试验色散量范围,横坐标为观测时间,CRAFTS超宽带数据每个观测文件为52 s,右侧子图描述试验色散量对应的信噪比大小。从图 1可以看到呈纺锤状的单脉冲事件组(在相邻的色散量与时间窗口内所有信噪比大于5的事件) 在最佳色散量78 pc·cm-3时取得峰值信噪比68,而在该色散量上下,信噪比下降。其中,强的脉冲星信号标记为Excellent;弱的脉冲星信号表标记为Very good;不规则的脉冲星信号标记为Good或Ok;射频干扰标记为RFI;宇宙噪声标记为Noise。在图 2中,我们看到在较宽的色散量范围上极强的射频干扰的实例。此外,在t=20~40 s,极强的射频干扰错误标记为脉冲星信号。

|
| 图 1 RRATtrap探测到脉冲星PSR B0540+23的诊断图 Fig. 1 Diagnostic picture of the pulsar PSR B0540+23 detected by RRATtrap |
|
| 图 2 RRATtrap筛选出假阳性实例的诊断图 Fig. 2 RRATtrap screened out false positive case diagnosis diagram |
本文试验选取2017年8月至2018年5月共计约32万个超宽带CRAFTS数据文件[1]进行单脉冲搜索试验。由于处理的数据规模较大,对所有数据进行全面的人工检查工作量非常大。因此,我们先使用RRATtrap初步筛选脉冲星候选体。然后,我们对数据文件中标记为Excellent,Very good,Good和Ok共计约5万颗脉冲星候选体的诊断图进行手工检查,发现仅有772个诊断图真正具有脉冲星信号,对应101颗已知脉冲星。通过
| $ FPR = \frac{{FP}}{{FP + TP}} $ | (1) |
计算的假阳性率(False Positive Rate, FPR) 达到98.5%,其中,FP是没有脉冲星信号的数据文件标记为候选脉冲星的数量;TP是含有脉冲星信号的数据文件标记为候选脉冲星的文件数量。每100个脉冲星候选体中,仅有1~2个包含脉冲星信号(已知或新发现的)。由于CRAFTS超宽带数据文件中包含的具体脉冲星数量未知,本文未对假阴性情况进行分析。
2 区分脉冲星信号和干扰的特征CRAFTS超宽带数据单脉冲搜索结果表明,脉冲星候选体仅有1.5%真正具有脉冲星信号,这主要是未能成功区分脉冲星信号和干扰造成的,如图 2。本节首先探讨不准确的色散量对信噪比的影响。然后,构造3个显著区分脉冲星信号和干扰的特征,并在探测到的101颗脉冲星样本中选取同时具有脉冲星信号、射频干扰和宇宙噪声的79颗脉冲星作为样本,计算它们在3个特征的取值情况。最后,根据脉冲星信号、射频干扰和宇宙噪声在3个特征取值分布的差异,提出合理阈值应用在单脉冲筛选工具,对脉冲星候选体进行进一步筛选。
2.1 色散量与信噪比曲线文[5]探讨了试验与真实色散量之间的偏差对信噪比的影响。通常,对一个特定色散量的时间序列进行多次下采样并重新搜索,当有效的采样时间最接近脉冲宽度时,得到的信噪比最高。在不同的色散量信道中,随着试验色散量与真实色散量的偏差越大,信噪比越小,如图 1。测量信噪比S(δDM) 与真实信噪比S的比值与色散量的偏差δDM满足[5]
| $ \frac{{S(\delta DM)}}{S} = \frac{{\sqrt {\rm{ \mathsf{ π} }} }}{2}{\zeta ^{ - 1}}erf\zeta , $ | (2) |
这里,
| $ \zeta = 6.91 \times {10^{ - 3}}\delta DM\frac{{\Delta {v_{{\rm{MHz}}}}}}{{W{v^3}}}. $ | (3) |
其中,erf为误差函数;δDM为试验色散量与真实色散量的偏差;Δv为总带宽;v为中心频率;W为脉冲宽度,单位ms。
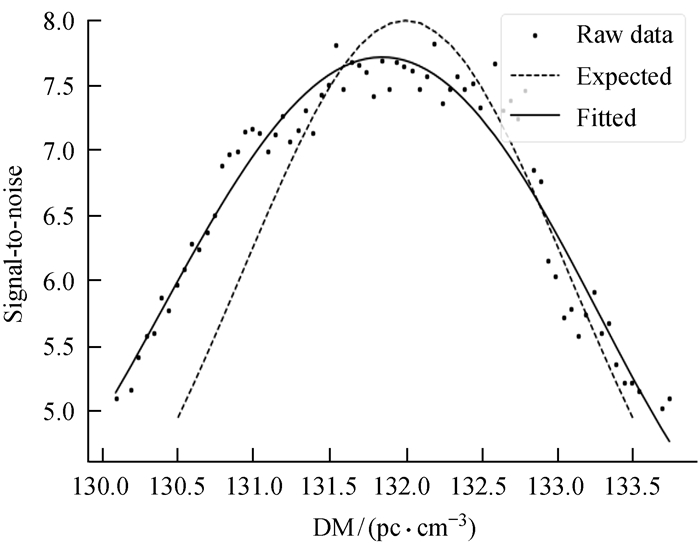
利用(2)式和(3) 式计算天体物理脉冲的信噪比和宽度,我们可以计算预期的色散量偏差δDM。图 3展示了在中心频率546 MHz,时间分辨率为100 μs和匹配滤波使用30的PSR B2000+40一组单脉冲事件预期和拟合信噪比下降曲线。在这两种情况下,信噪比峰值处的色散量是真实的色散量。我们计算预期的信噪比下降,利用峰值信噪比和匹配滤波得到脉冲宽度,和实际脉冲宽度很接近。首先,我们使用非线性最小二乘法(Non-linear Least Squares, NLS) 对原始数据进行回归,得到拟合的峰值信噪比和脉冲宽度。然后,根据拟合结果,代入(2) 式得到拟合的色散与信噪比曲线。由图 3可以看出,预期和拟合的色散量与信噪比曲线大致是高斯曲线。使用观测到的峰值信噪比和匹配滤波得到脉冲宽度,预期的信噪比下降与拟合值在峰值右侧非常接近,但在左侧出现偏差。这是匹配滤波得到的脉冲宽度与实际脉冲宽度的偏差造成的。
|
| 图 3 PSR B2000+40一组单脉冲事件色散与信噪比曲线图 Fig. 3 PSR B2000+40 a set of single pulse event dispersion and signal-to-noise ratio curve |
文[13]指出,脉冲星的轮廓可以简化为高斯型(对大多数脉冲星来说是一个合理的近似)。按照文[5]提出的单脉冲搜索理论,天体物理脉冲的色散量和信噪比曲线大致是高斯曲线,如图 3。由于高斯曲线通常是对称的,文[14]提出了两种对称特征(SIDM和SIS/N) 分别表征单脉冲事件组的色散量和信噪比的对称性。SIDM的计算公式为
| $ S{I_{{\rm{DM}}}} = \frac{{\min \left( {D{M_{\max }} - D{M_{{\rm{peak }}}}\;, D{M_{{\rm{peak }}}} - D{M_{{\rm{min }}}}} \right)}}{{\max \left( {D{M_{\max }} - D{M_{{\rm{peak }}}}\;, D{M_{{\rm{peak }}}} - D{M_{\min }}} \right)}}. $ | (4) |
其中,DMpeak为信噪比峰值对应的色散量;DMmax为单脉冲事件组最大的色散量;DMmin为单脉冲事件组最小的色散量。SIS/N的计算公式为
| $ S{I_{{\rm{S}}/{\rm{N}}}} = \frac{{\min \left( {\sum S /{N_{{\rm{left }}}}, \sum S /{N_{{\rm{right }}}}} \right)}}{{\max \left( {\sum S /{N_{{\rm{left }}}}, \sum S /{N_{{\rm{right }}}}} \right)}}. $ | (5) |
其中,∑S/Nleft为信噪比峰值左侧所有单脉冲事件的信噪比之和;∑S/Nright为信噪比峰值右侧所有单脉冲事件的信噪比之和。
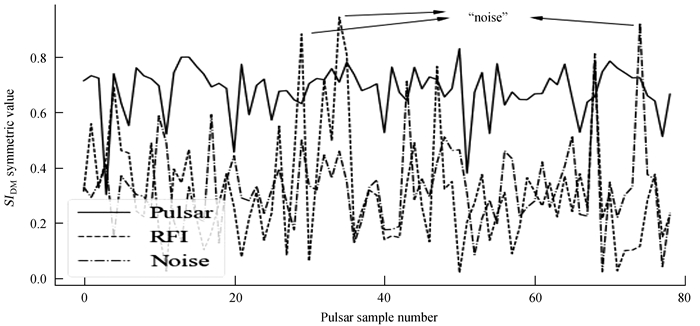
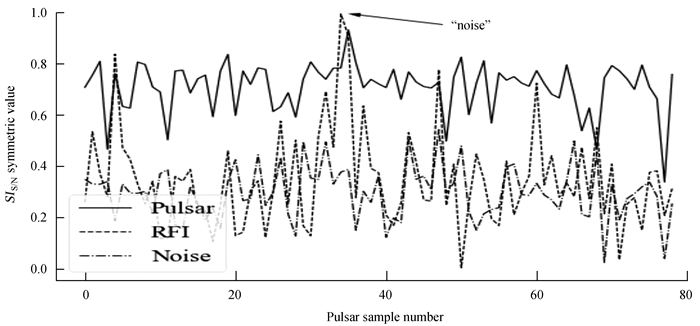
由(4)式和(5) 式定义的SIDM和SIS/N的取值范围在0~1之间,这两个特征值越高,色散量与信噪比曲线越对称,相反不遵循(2) 式描述规律的射频干扰,通常在色散量与信噪比空间是单调递减(或递增)。所以,它们通常具有接近于0的对称值,可以与脉冲星信号进行区分。图 4和图 5分别展示了脉冲星样本SIDM和SIS/N的对称值,并对脉冲星信号、射频干扰和噪声进行了对比。从图 4和图 5可以看出,脉冲星信号通常具有较大的对称值,而射频干扰和噪声的对称值相对较小,这表明脉冲星信号的色散量和信噪比曲线比干扰更对称。此外,图 4和图 5标记一些对称值比较大的噪声,这些通常是高斯噪声。
|
| 图 4 脉冲星样本SIDM对称值 Fig. 4 SIDM Symmetry values of pulsar samples |
|
| 图 5 脉冲星样本SIS/N对称值 Fig. 5 SIS/N Symmetry values of pulsar samples |
文[5]预测在没有任何宇宙噪声和射频干扰的情况下,信噪比的数据分布是高斯分布。峰度是描述总体数据分布与高斯分布陡缓程度的统计量。为了判断脉冲星样本信噪比的数据分布是否符合高斯分布,我们使用峰度值表征单脉冲事件组内信噪比的数据分布与高斯分布的符合程度。峰度值的计算公式为
| $ kurtosis[S/N] = E\left[ {{{\left( {\frac{{S/N - \mu }}{\sigma }} \right)}^4}} \right] = \frac{{E\left[ {{{(S/N - \mu )}^4}} \right]}}{{{{\left\{ {E\left[ {{{(S/N - \mu )}^2}} \right]} \right\}}^2}}}. $ | (6) |
其中,S/N为单脉冲事件的信噪比;μ为单脉冲事件组内平均信噪比;σ为单脉冲事件组内信噪比的方差。
当(6) 式定义的峰度值是3时,信噪比的数据分布服从高斯分布,随着峰度值与3的差距越大,其分布形态的陡缓程度与高斯分布的差异程度越大。图 6用箱线图展示了脉冲星样本的峰度值分布情况,并对脉冲星信号、射频干扰和噪声进行了对比。从图 6可以看出,脉冲星信号峰度值集中在3附近,而射频干扰和噪声的峰度值分散,且与3差距较大,表明脉冲星信号信噪比分布近似服从高斯分布,而大部分干扰与噪声不具有此规律。

|
| 图 6 脉冲星样本峰度值 Fig. 6 Kurtosis value of pulsar sample |
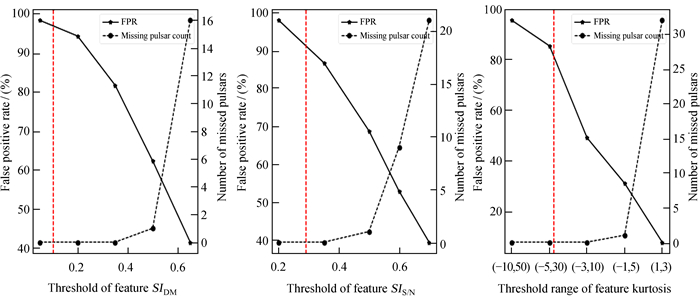
图 4~图 6可以明显看出脉冲星信号、射频干扰和宇宙噪声在3个特征分布的差异。因此,我们根据脉冲星信号和干扰特征值的分布区间(表 1),选择合适的特征阈值,剔除不满足阈值的脉冲星候选体,从而达到降低假阳性率的目的(比如设置脉冲星信号特征SIDM最小值0.1作为阈值,对低于阈值的候选体视为干扰,那么,特征值在0.02~0.1区间的射频干扰将不会错误标记为脉冲星候选体)。同时,我们选取不同阈值进行试验,并统计其对应的假阳性率和遗漏脉冲星信号的结果。由图 7各个特征在不同阈值假阳性及遗漏脉冲星的情况可以看出,随着阈值变大或者阈值区间缩小,假阳性率不断减小,与此同时,遗漏发现的脉冲星数量在不断增加。脉冲星搜寻的首要前提是保证观测数据中所有脉冲星信号不遗漏。因此,我们选取表 1中脉冲星信号特征SIDM最小值0.1和SIS/N最小值0.29作为阈值,特征峰度-1.54~27.11作为阈值区间,对低于阈值或不在阈值区间的脉冲星候选体视为射频干扰或宇宙噪声。
| Features | Pulsar | RFI | Noise | |||
| CRAFTS | PMPS | CRAFTS | CRAFTS | |||
| SIDM | 0.10~0.97 | 0.25~0.90 | 0.02~0.92 | 0.01~0.94 | ||
| SIS/N | 0.29~0.96 | 0.26~0.96 | 0.01~0.99 | 0.02~0.54 | ||
| Kurtosis | -1.54~27.11 | -0.81~23.38 | -0.80~28.95 | 0.74~31.58 | ||
|
| 图 7 各个特征在不同阈值假阳性和遗漏脉冲星的情况,其中红色竖线代表所选择的阈值 Fig. 7 Each feature has different thresholds for false positives and missing pulsars, where the red vertical line represents the selected threshold |
此外,为了证实所述特征是否在其他观测数据有效,我们对帕克斯多波束数据进行了试验。根据文[15]公开的帕克斯单脉冲数据库,我们构建了一个PMPS (Parkes Multibeam Pulsar Survey) 数据库,其中包含帕克斯望远镜发现的部分脉冲星信号。我们计算得到PMPS数据集中脉冲星信号在3个特征值的分布情况,并与CRAFTS进行对比,如表 1。由表 1中CRAFTS及PMPS的脉冲星信号在3个特征值分布情况可以发现,它们的特征值分布十分接近,尽管它们在消色散网格、周围射频干扰的环境等存在显著差异。因此,本文所述的特征阈值同样能够区分帕克斯数据库中脉冲星信号和干扰。
我们将上述阈值和阈值区间应用于单脉冲筛选工具,对脉冲星候选体进行重新筛选,试验结果如表 2。由表 2可以看出,添加单个特征阈值判断的单脉冲筛选工具能在一定程度上降低假阳性率,并且3个特征阈值组合判断假阳性率从98.5%降低到78.4%,表明添加特征阈值判断的单脉冲筛选工具提高了脉冲星搜索效率。
| Features | False Positive Rate (FPR)/(%) |
| SIDM | 97.9 |
| SIS/N | 93.8 |
| Kurtosis | 82.5 |
| SIDM+ SIS/N+ kurtosis | 78.4 |
本文使用PRESTO的单脉冲搜索方法对CRAFTS超宽带数据文件进行的试验表明,现有的单脉冲筛选工具难以区分真实信号与噪声或射频干扰信号,造成数以万计的假阳性样本出现,显著增加人工筛选单脉冲候选体的时间开销以及候选数据存储压力。因此,我们提出3个显著区分脉冲星信号和干扰的特征,并选取同时具有脉冲星信号、射频干扰和宇宙噪声的79颗脉冲星样本,计算它们在3个特征取值情况。然后,根据脉冲星信号、射频干扰和宇宙噪声在3个特征取值分布的差异,提出合理阈值应用于单脉冲筛选工具,用于对脉冲星候选体进行严格的判断。最后,使用添加特征阈值判断的筛选工具对脉冲星候选体进行重新试验。结果表明,在保证所有脉冲星信号不遗漏的情况下,假阳性率从98.5%降低到78.4%。因此,本文所述3个特征具有实用性和有效性,有助于单脉冲搜索在CRAFTS巡天数据的应用。
致谢: 本文在500 m口径球面射电望远镜(FAST) 数据基础上完成。FAST是由中国科学院国家天文台运行和管理的国家大科学装置。感谢中国科学院天文大科学研究中心FAST重大成果培育项目对本文工作的资助。
| [1] | LORIMER D R, KRAMER M. Handbook of pulsar astronomy[M]. Cambridge: Cambridge University Press, 2004. |
| [2] | LARSSON S. Parameter estimation in epoch folding analysis[J]. Astronomy and Astrophysics Supplement Series, 1996, 117(1): 197–201. DOI: 10.1051/aas:1996150 |
| [3] | MCLAUGHLIN M A, LYNE A, LORIMER D, et al. Transient radio bursts from rotating neutron stars[J]. Nature, 2006, 439: 817–820. DOI: 10.1038/nature04440 |
| [4] | LORIMER D R, BAILES M, MCLAUGHLIN M A, et al. A bright millisecond radio burst of extragalactic origin[J]. Science, 2007, 318: 777–780. DOI: 10.1126/science.1147532 |
| [5] | CORDES J M, MCLAUGHLIN M A. Searches for fast radio transients[J]. The Astrophysical Journal, 2003, 596(2): 1142–1154. DOI: 10.1086/378231 |
| [6] | DENEVA J S, CORDES J M, MCLAUGHLIN M A, et al. Arecibo pulsar survey using ALFA: probing radio pulsar intermittency and transients[J]. The Astrophysical Journal, 2009, 703(2): 2259–2274. DOI: 10.1088/0004-637X/703/2/2259 |
| [7] | KEANE E F, LUDOVICI D A, EATOUGH R P, et al. Further searches for rotating radio transients in the parkes multi-beam pulsar survey[J]. Monthly Notices of the Royal Astronomical Society, 2010, 401(1): 1057–1068. |
| [8] | KARAKO-ARGAMAN C, KASPI V M, LYNCH R S, et al. Discovery and follow-up of rotating radio transients with the Green Bank and LOFAR telescopes[J]. The Astrophysical Journal, 2015, 809(1): 67. DOI: 10.1088/0004-637X/809/1/67 |
| [9] | DEVINE T R, KATERINA G P, MAURA M L. Detection of dispersed radio pulses: a machine learning approach to candidate identification and classification[J]. Monthly Notices of the Royal Astronomical Society, 2016, 459(1): 1519–1532. |
| [10] |
刘鹏, 王培, 李菂, 等. FAST 19波束脉冲星漂移扫描巡天模拟[J]. 天文学进展, 2018, 36(2): 173–188 LIU P, WANG P, LI D, et al. FAST 19-beam pulsar drift scan survey simulation[J]. Progress in Astronomy, 2018, 36(2): 173–188. |
| [11] | LI D, WANG P, QIAN L, et al. FAST in space: considerations for a multi-beam multipurpose survey using China's 500-m aperture spherical radio telescope (FAST)[J]. IEEE Microwave Magazine, 2018, 19(3): 112–119. DOI: 10.1109/MMM.2018.2802178 |
| [12] | CORDES J M. Pulsar observations Ⅰ.-Propagation effects, searching distance estimates, scintillations and VLBI[C] // Proceedings of ASP Conference. 2002: 278-286. |
| [13] | LORIMER D R, FAULKNER A J, LYNE A G, et al. The parkes multibeam pulsar survey-Ⅵ. Discovery and timing of 142 pulsars and a galactic population analysis[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(2): 777–800. DOI: 10.1111/j.1365-2966.2006.10887.x |
| [14] | PANG D, GOSEVA-POPSTOJANOVA K, DEVINE T, et al. A novel single-pulse search approach to detection of dispersed radiopulses using clustering and supervised machine learning[J]. Monthly Notices of the Royal Astronomical Society, 2018, 459(2): 1519–1541. |
| [15] | ZHANG S B, HOBBS G, RUSSELL C J, et al. Parkes transient events: Ⅰ. Database of single pulses, initial results and missing FRBs[J]. The Astrophysical Journal, 2020, 249(1): 14. DOI: 10.3847/1538-4365/ab95a4 |



