2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
激光测距技术通过精确测定激光脉冲在地面观测站和目标之间的往返时间,并根据光速计算地面观测站和目标间的距离[1]。作为目前最精确的测量手段,激光测距的目标主要有合作目标(携带角反射器)、空间碎片和月球,观测数据对天文地球动力学、月球物理和引力理论等诸多科学研究有重要的价值。
在激光测距中,不同高度的目标受到的摄动影响不同,轨道的预报精度也不同,高轨道目标的预报精度优于低轨道目标的[2]。对于低轨目标,可以通过增大发散角增加激光到达目标表面时的光束面积,有利于目标的搜索;而对于高轨目标,应减小发散角,以增加激光到达目标表面时的能量密度,有利于提高探测成功的概率。因此,为满足不同距离目标的测距要求,我们通常采用扩束系统调整激光发散角。
目前,云南天文台及国内大部分激光测距台站采用倒置的伽利略式望远镜扩束系统调整光束发散角。通过移动扩束系统中的凹透镜调整两透镜间的距离来改变发散角,称为离焦式扩束系统,距离的调整量称为离焦量。该方式调整发散角时,系统不再是共焦状态,光束波前不再是平面波,存在波前畸变,从而产生离焦像差,影响光束质量,降低回波信号的强度,进而影响系统的测距能力。因此,研究离焦像差对回波光子数的影响具有重要意义。文[3]研究了不同类型波像差和斯特列尔比之间的关系,并建立了拟合关系式。文[4]研究了光束控制系统热效应和球差对远场激光光束质量的影响,结果表明,传输通道的热效应和正球差使远场光强分布扩展,聚焦能力下降,光束质量变差。文[5]研究了光学系统的波像差与对应的光束质量β因子间的关系,用数值计算方法建立了各种泽尼克多项式的波像差均方根(Root Mean Square, RMS) 与β因子间的拟合关系式。
综上,像差对激光光束质量如β因子、斯特列尔比和聚焦性等有很大的影响,但光束质量对系统测距能力的影响未见相关文献报道。本文采用光束能量密度的空间分布来描述光束质量,利用激光测距回波光子数表示测距系统的测距能力,研究离焦像差对光束质量和系统测距能力的影响,具有重要的理论价值。
1 理论模型 1.1 基模高斯光束的传播及基本性质由激光谐振腔衍射理论可知,在均匀的透明介质中,基模高斯光束沿z轴方向传播的复振幅为[6-8]
| $ A(x, y, z)=\sqrt{\frac{2 E_{0}}{\pi}} \frac{1}{\omega(z)} \exp \left[-\frac{x^{2}+y^{2}}{\omega^{2}(z)}\right] \exp \left(-\mathrm{i}\left\{k\left[\frac{x^{2}+y^{2}}{2 R(z)}+z\right]-{\mathit{\Phi}}(z)\right\}\right), $ | (1) |
其中,各项参数表达式为[6]
| $ \omega(z)=\omega_{0}\left[1+\left(\frac{\lambda z}{\pi \omega_{0}^{2}}\right)^{2}\right]^{\frac{1}{2}}=\omega_{0}\left[1+\left(\frac{z}{Z_{0}}\right)^{2}\right]^{\frac{1}{2}}, $ | (2) |
| $ R(z)=z\left[1+\left(\frac{\pi \omega_{0}^{2}}{\lambda z}\right)^{2}\right]=z\left[1+\left(\frac{Z_{0}}{z}\right)^{2}\right], $ | (3) |
| $ {\mathit{\Phi}}(z)=\arctan \left(z / Z_{0}\right) . $ | (4) |
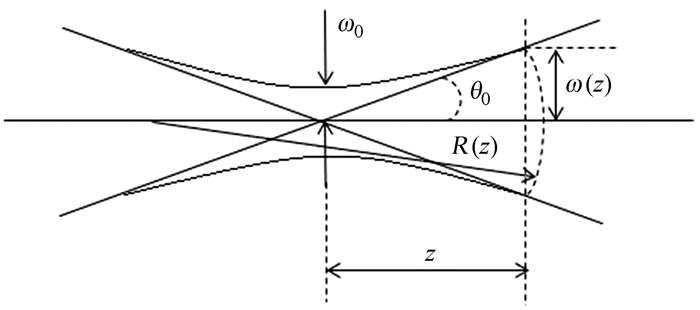
上述各式中,E0为激光单脉冲能量;λ为光束波长;k=2π/λ为波数;ω(z),R(z)和Φ(z) 分别为基模高斯光束的截面半径、波面曲率半径和位相因子,是基模高斯光束复振幅分布的3个重要参数,当z=0时,ω0=ω(0) 是光束截面最小处的光束截面半径,称为光束的束腰半径;Z0=πω02/λ=0.5kω02,称为瑞利长度或共焦参数。基模高斯光束的传播如图 1。
|
| 图 1 基模高斯光束的传播 Fig. 1 Propagation of fundamental mode Gaussian beams |
基模高斯光束的远场发散半角θ0是双曲线的渐近线与光束对称轴的夹角,定义为[7]
| $ \theta_{0}=\lim\limits _{z \rightarrow \infty} \frac{\omega(z)}{z} . $ | (5) |
结合(2)式和(5) 式,求极限得
| $ \theta_{0}=\frac{\lambda}{\pi \omega_{0}}. $ | (6) |
基模高斯光束经过扩束系统后,束腰半径和束腰位置改变。由(1) 式可知,束腰半径影响光束的复振幅分布。因此,我们需要根据矩阵光学求出光束经扩束系统后的束腰半径和束腰位置。
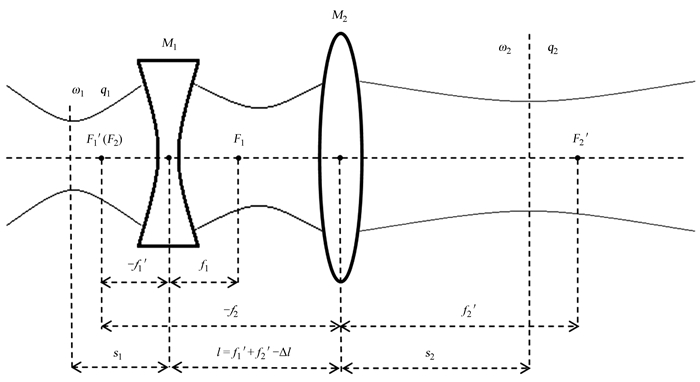
图 2为基模高斯光束经扩束系统后的变换。假设s1为束腰ω1与透镜M1间的距离,由透镜M1指向束腰ω1;s2为束腰ω2与透镜M2间的距离,由透镜M2指向束腰ω2。透镜M1和M2间的距离为l=f1′+f2′-Δl,由M2指向M1,其中,f1′和f2′分别为M1,M2的像方焦距;Δl为离焦量,由F2指向F1′。以上各量从左到右为正,反之为负。设放大率MT= f2′/f1′,则扩束系统的变换矩阵为[7]
| $ \boldsymbol{m}=\left[\begin{array}{cc} M_{\mathrm{T}}+\frac{\Delta l}{f_{1}{ }^{\prime}} & l \\ -\frac{\Delta l}{f_{1}^{\prime} f_{2}^{\prime}} & \frac{1}{M_{\mathrm{T}}}+\frac{\Delta l}{f_{2}{ }^{\prime}} \end{array}\right] {. } $ | (7) |
|
| 图 2 基模高斯光束经扩束系统后的变换 Fig. 2 Transformation of fundamental mode Gaussian beam through beam expanding system |
束腰ω1到束腰ω2的变换矩阵为
| $ \boldsymbol{M}_{\omega_{1}, \omega_{2}}=\left[\begin{array}{cc} 1 & s_{2} \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} M_{\mathrm{T}}+\frac{\Delta l}{f_{1}{ }^{\prime}} & l \\ -\frac{\Delta l}{f_{1}{ }^{\prime} f_{2}{ }^{\prime}} & \frac{1}{M_{\mathrm{T}}}+\frac{\Delta l}{f_{2}^{\prime}} \end{array}\right]\left[\begin{array}{cc} 1 & s_{1} \\ 0 & 1 \end{array}\right] . $ | (8) |
当离焦量Δl=0时,s2, ω2和ω1之间的关系为[7]
| $ s_{2}=-M_{\mathrm{T}}\left(f_{1}^{\prime}+f_{2}^{\prime}\right)-M_{\mathrm{T}}^{2} s_{1}, $ | (9) |
| $ \omega_{2}=M_{\mathrm{T}} \omega_{1} . $ | (10) |
当离焦量Δl≠0时,略去Δl的二级小量,s2′, ω2′和ω1之间关系为[7]
| $ s_{2}^{\prime}=f_{2}^{\prime}-M_{\mathrm{T}}^{2}\left(s_{1}-f_{1}^{\prime}\right)+M_{\mathrm{T}}^{2} \Delta l\left[\left(1-\frac{s_{1}}{f_{1}^{\prime}}\right)^{2}-\left(\frac{Z_{1}}{f_{1}^{\prime}}\right)^{2}\right], $ | (11) |
| $ \omega_{2}^{\prime}=\omega_{1} \sqrt{\frac{(\Delta l)^{2}}{M_{\mathrm{T}}^{2} f_{1}^{\prime 2}}+\frac{2 \Delta l}{f_{1}^{\prime} M_{\mathrm{T}}^{2}}+\frac{1}{M_{\mathrm{T}}^{2}}} . $ | (12) |
定义角放大率为高斯光束扩束后与扩束前光束发散角的比值,由(6) 式可知,高斯光束的发散角与束腰半径成反比。当离焦量Δl=0时,由(10) 式得角放大率α为
| $ \alpha=\frac{\theta_{2}}{\theta_{1}}=\frac{\omega_{1}}{\omega_{2}}=\frac{1}{M_{\mathrm{T}}} ; $ | (13) |
当离焦量Δl≠0时,由(12) 式得角放大率α′为
| $ \alpha^{\prime}=\frac{\theta_{2}{ }^{\prime}}{\theta_{1}^{\prime}}=\frac{\omega_{1}}{\omega_{2}{ }^{\prime}}=\frac{1}{\sqrt{\frac{\Delta l^{2}}{M_{\mathrm{T}}^{2} f_{1}^{\prime 2}}+\frac{2 \Delta l}{f_{1}{ }^{\prime} M_{\mathrm{T}}^{2}}+\frac{1}{M_{\mathrm{T}}^{2}}}} . $ | (14) |
调整离焦量后,扩束系统不再是共焦状态,光束波前存在畸变,影响光束能量密度的空间分布。波面上的光程总是相等的,波像差是实际波面和理想波面之间的光程差。波像差一般没有数学解析表达式,常用有限项泽尼克多项式近似表达,离焦像差用泽尼克多项式表示为[9]
| $ W_{4}(x, y)=a_{4} Z_{4}(x, y)=a_{4}\left(2 \sqrt{3} x^{2}+2 \sqrt{3} y^{2}-\sqrt{3}\right), $ | (15) |
其中,W4(x, y) 为离焦像差函数;a4为泽尼克多项式系数(单位为波长λ),表示像差的标准差,即波前的均方根;Z4(x, y) 为泽尼克多项式的项,可以表示为
| $ \Delta l=8 \delta\left(\frac{F M_{\mathrm{T}}}{D}\right)^{2}=8 \delta\left(\frac{F}{D \alpha}\right)^{2} $ | (16) |
其中,Δl为离焦量;δ为离焦像差产生的波前峰谷差;F为望远镜的有效焦距;D为望远镜主镜的口径;α为角放大率。离焦像差的泽尼克多项式系数a4与波前峰谷差δ满足关系[10]
| $ \delta=2 \sqrt{3} a_{4} \lambda=\frac{\Delta l}{8}\left(\frac{D \alpha}{F}\right)^{2} . $ | (17) |
由(16)式和(17) 式得泽尼克多项式系数a4与离焦量Δl关系为
| $ a_{4}=\frac{\delta}{2 \sqrt{3} \lambda}=\frac{\Delta l}{16 \sqrt{3} \lambda}\left(\frac{D \alpha}{F}\right)^{2} . $ | (18) |
由(18) 式可知,在望远镜主镜口径D和有效焦距F确定后,泽尼克多项式系数a4与离焦量Δl对应。
由于扩束系统存在衍射效应和离焦像差,激光经过扩束系统后不仅发生衍射,而且与未发生衍射的光(直射光) 相互干涉,影响光斑的能量密度分布[6]。有离焦像差时,高斯光束在垂直于z轴平面内的复振幅分布为
| $ \begin{aligned} I(x, y)=& \frac{1}{\omega(z)} \sqrt{\frac{E_{0}}{2 \pi}} \exp \left[-\frac{x^{2}+y^{2}}{\omega^{2}(z)}\right] \exp \left(-\mathrm{i}\left\{k\left[\frac{x^{2}+y^{2}}{2 R(z)}+z\right]-{\mathit{\Phi}}(z)\right\}\right) \\ &\left\{1+\exp \left[\mathrm{i} k W_{4}(x, y)\right]\right\} . \end{aligned} $ | (19) |
当无离焦像差时,离焦量Δl=0,泽尼克多项式系数a4=0,则像差项W4(x, y)=0, exp ikW4(x, y) 的值恒为1,此时,(19)式等价于(1) 式,光束的复振幅符合理想高斯分布。当有离焦像差时,离焦量Δl≠0,由(18) 式可知,泽尼克多项式系数a4随离焦量Δl的增大而增大(结果见表 1),影响光束的复振幅分布。
光束能量密度为
| $ E d(x, y)=I(x, y) I^{*}(x, y), $ | (20) |
| Angle magnification α | Defocusing amount Δ l/mm | Aberration standard deviation a4/λ |
| 0.2 | 26.8 | 1.2 |
| 0.3 | 76.7 | 7.6 |
| 0.4 | 126.6 | 22.4 |
| 0.5 | 176.4 | 48.6 |
| 0.6 | 226.3 | 89.9 |
| 0.7 | 276.2 | 149.3 |
| 0.8 | 326.1 | 230.2 |
| 0.9 | 376.0 | 336.0 |
其中,I *(x, y)为I(x, y)的共轭。测距目标接收的激光能量为
| $ E=\iint\limits_{S} E d(x, y) \mathrm{d} S, $ | (21) |
其中,S为测距目标的有效反射面积。
1.4 激光测距回波光子数以卫星为探测目标,激光测距时,探测器接收的回波光子数n为[11-12]
| $ n=\frac{E N \rho A_{\mathrm{r}} A_{\mathrm{s}} \eta_{\mathrm{t}} \eta_{\mathrm{r}} T^{2} \eta \beta}{\pi^{2} R^{4} \theta_{\mathrm{e}}^{2} \theta_{\mathrm{m}}^{2}}, $ | (22) |
其中,N=λ/hc为每焦耳激光能量所含的光子数,式中λ为激光波长,h为普朗克常量,c为真空中的光速;ρ为卫星角反射器的反射率;Ar为望远镜有效接收面积;As为卫星角反射器的有效反射面积;ηt为激光发射系统的光学效率;ηr为测距系统的接收效率;T为单程大气光学透过率;η为探测器的量子效率;β为衰减因子(受大气抖动、湍流等影响);R为卫星到测距台站的距离;θe为激光的发散半角;θm为激光经卫星角反射器反射后的发散半角。(22) 式即为激光测距回波光子数方程。
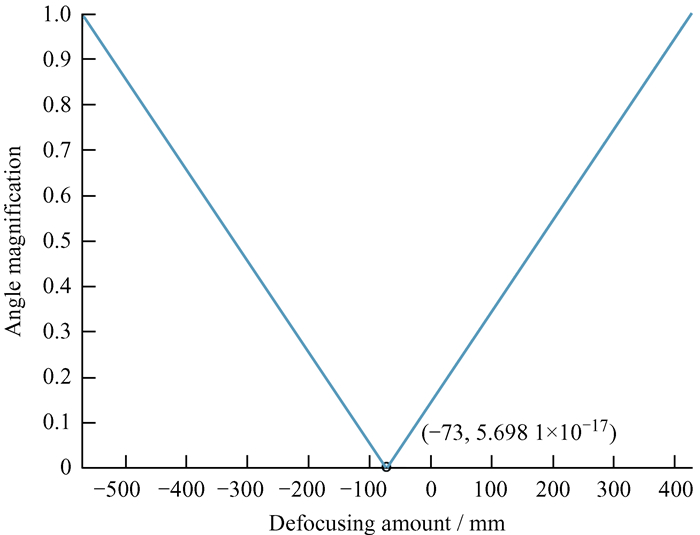
2 结果分析与讨论 2.1 角放大率和离焦量关系云南天文台53 cm望远镜激光测距系统中一级扩束系统的凹透镜像方焦距f1′=-73 mm,凸透镜像方焦距f2′=498.79 mm。离焦量Δl的变化范围为-571.9 mm~425.79 mm。我们把上述参数代入(14) 式,得到角放大率和离焦量的关系,如图 3和表 1。由图 3可知,角放大率关于Δl=-73 mm对称分布。随着离焦量增大,角放大率逐渐增大。当离焦量为-73 mm时,角放大率最小,趋向于无穷小,此时,凹透镜位于凸透镜物方焦点处。由(14) 式可知,离焦量Δl不能等于-73 mm,故角放大率不可能为0。表 1中的数据线性拟合结果表明,角放大率和离焦量近似符合线性关系,离焦量每增加1 mm,角放大率增加0.002。
|
| 图 3 角放大率和离焦量关系 Fig. 3 Relationship between angle magnification and defocusing amount |
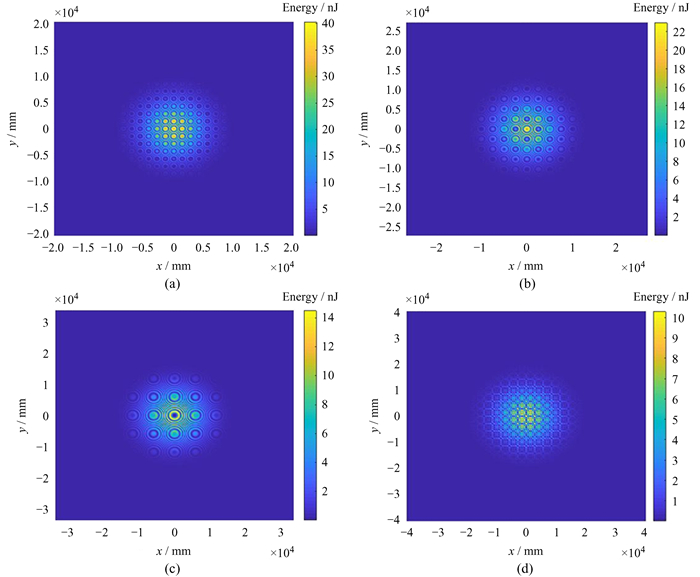
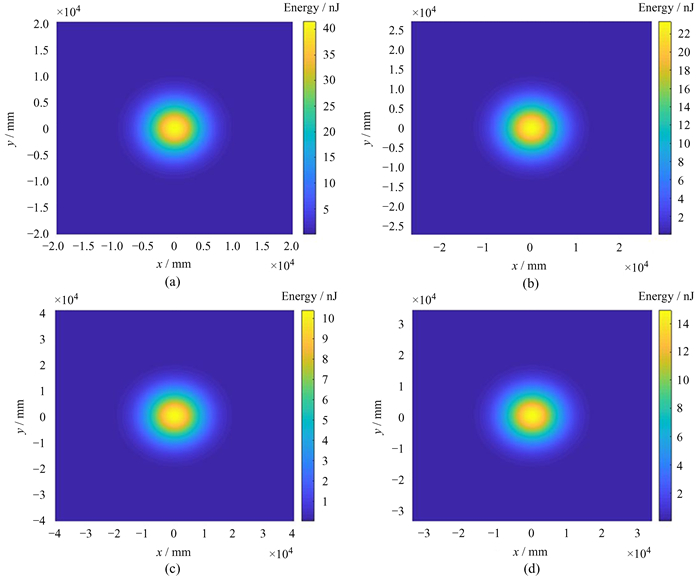
测距系统中发射激光波长λ=532 nm,光束束腰半径ω0=7.5 mm,激光发散半角θ0=0.5 mrad[13]。假设卫星与测距台站间距离R=1 000 km,卫星角反射器的有效反射区域为边长1 m的正方形,光束中心和卫星角反射器有效反射区域中心重合。把上述参数代入(19) 式,得到不同角放大率下光束在1 000 km处的能量密度分布,结果见图 4和图 5。图中激光发散角为激光经过扩束系统后的发散角,由角放大率乘以入射激光发散角求得,光斑半径由(2) 式求得。由图 4和图 5可知,光束经过扩束系统后,随着激光发散角的增大,光斑半径逐渐增大。当无离焦像差时,光斑半径仅发生尺度变化,能量密度分布符合高斯分布;当有离焦像差时,光斑半径不仅发生尺度变化,而且形状更加弥散,能量密度分布也不再是高斯分布,变得更为复杂。
|
| 图 4 有离焦像差时光束能量密度分布。(a) 发散角θ=0.15 mrad,光斑半径r=6.78 m;(b) 发散角θ=0.2 mrad,光斑半径r=9.04 m;(c) 发散角θ=0.25 mrad,光斑半径r=11.29 m;(d) 发散角θ=0.3 mrad,光斑半径r=13.57 m Fig. 4 Beam energy density distribution in the presence of defocusing aberrations. (a) divergence angle θ=0.15 mrad, spot radius r=6.78 m; (b) divergence angle θ=0.2 mrad, spot radius r=9.04 m; (c) divergence angle θ=0.25 mrad, spot radius r=11.29 m; (d) divergence angle θ=0.3 mrad, spot radius r=13.57 m |
|
| 图 5 无离焦像差时光束能量密度分布。(a) 发散角θ=0.15 mrad,光斑半径r=6.78 m;(b) 发散角θ=0.2 mrad,光斑半径r=9.04 m;(c) 发散角θ=0.25 mrad,光斑半径r=11.29 m;(d) 发散角θ=0.3 mrad,光斑半径r=13.57 m Fig. 5 Energy density distribution of beam without defocusing aberration.(a) divergence angle θ=0.15 mrad, spot radius r=6.78 m; (b) divergence angle θ=0.2 mrad, spot radius r=9.04 m; (c) divergence angle θ=0.25 mrad, spot radius r=11.29 m; (d) divergence angle θ=0.3 mrad, spot radius r=13.57 m |
利用(21) 式计算当卫星到测距台站的距离R=1 000 km时,卫星在不同角放大率下接收的能量如表 2。表 2中E1为有离焦像差时卫星接收的能量,E2为无离焦像差时卫星接收的能量。由表 2可知,在不同角放大率下,E2均大于E1。因此,离焦像差影响激光光束的能量密度分布,进而影响卫星接收的能量。
| Angle magnification α | Energy E1/mJ | Energy E2/mJ |
| 0.200 1 | 45.9 | 92.0 |
| 0.300 1 | 20.9 | 41.3 |
| 0.400 2 | 11.7 | 23.3 |
| 0.500 0 | 7.5 | 14.9 |
| 0.600 1 | 5.2 | 10.4 |
| 0.700 1 | 3.8 | 7.6 |
| 0.800 1 | 2.9 | 5.8 |
| 0.900 2 | 2.3 | 4.6 |
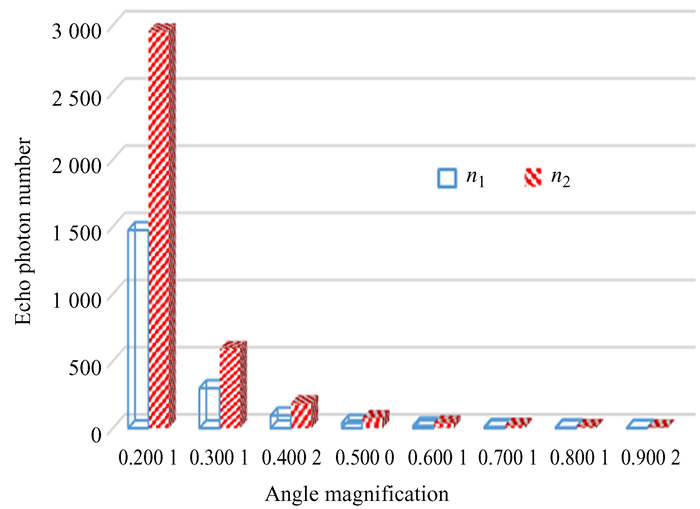
云南天文台53 cm望远镜激光测距系统的参数为激光单脉冲能量E0=3 J,每焦耳激光能量所含光子数N=2.7×1018 (激光波长λ=532 nm),卫星角反射器的反射率ρ=0.8,卫星角反射器的有效反射面积As=1 m2,望远镜有效接收面积Ar=0.204 3 m2,激光发射系统的光学效率ηt=0.5,测距系统的接收效率ηr=0.5,单程大气的光学透过率T=0.6,单光子雪崩二极管探测器的量子效率η=0.2,衰减因子β=0.1,地面测距台站到卫星的距离R的范围为500~1 000 km、距离间隔100 km,激光光束经卫星角反射器反射后的发散角θm=0.5 mrad。把上述参数代入(22) 式计算回波光子数,结果如图 6、表 3和表 4。图 6为距离R=1 000 km时不同角放大率的回波光子数,n1为有离焦像差时的回波光子数,n2为无离焦像差时的回波光子数。如图 6,对于距离R=1 000 km处的卫星,随着角放大率的增大,测距系统接收的回波光子数迅速衰减。因此,对于不同距离的目标,需要选择适当的激光发散角。表 3和表 4为卫星与测距台站间距离R取不同值时测距系统接收的回波光子数。由表 3和表 4可知,当激光发散半角相同时,卫星离测距站越近,测距系统接收的回波光子数越多。对于同一距离的卫星,激光发散半角越小,测距系统接收的回波光子数越多。对于不同距离的同一颗卫星,在不同角放大率下,n1均小于n2,前者约为后者的50%。回波光子数越多,目标的探测成功概率越高。
|
| 图 6 激光测距回波光子数 Fig. 6 The number of echo photons in laser ranging |
| Angle magnification α | R=500 km | R=600 km | R=700 km | |||||
| aberration n1 | no aberration n2 | aberration n1 | no aberration n2 | aberration n1 | no aberration n2 | |||
| 0.200 1 | 89 907.6 | 180 277.9 | 30 715.2 | 61 579.1 | 12 324.1 | 24 715.0 | ||
| 0.300 1 | 18 644.9 | 36 969.6 | 6 299.6 | 12 488.9 | 2 519.0 | 4 978.5 | ||
| 0.400 2 | 5 943.2 | 11 835.0 | 1 997.6 | 3 982.8 | 793.6 | 1 583.9 | ||
| 0.500 0 | 2 464.1 | 4 887.1 | 826.7 | 1 641.4 | 328.2 | 652.2 | ||
| 0.600 1 | 1 178.6 | 2 362.9 | 397.3 | 794.6 | 157.9 | 315.7 | ||
| 0.700 1 | 638.9 | 1 277.9 | 214.9 | 429.8 | 85.3 | 170.7 | ||
| 0.800 1 | 373.3 | 749.9 | 125.7 | 251.4 | 49.4 | 99.7 | ||
| 0.900 2 | 233.9 | 467.8 | 78.5 | 156.9 | 31.1 | 62.2 | ||
| Angle magnification α | R=800 km | R=900 km | R=1 000 km | |||||
| aberration n1 | no aberration n2 | aberration n1 | no aberration n2 | aberration n1 | no aberration n2 | |||
| 0.200 1 | 5 576.9 | 11 177.4 | 2 761.8 | 5 543.2 | 1 474.7 | 2 955.8 | ||
| 0.300 1 | 1 134.5 | 2 244.6 | 560.1 | 1 109.3 | 298.8 | 590.5 | ||
| 0.400 2 | 357.2 | 712.5 | 176.5 | 351.7 | 94.1 | 187.3 | ||
| 0.500 0 | 148.4 | 293.0 | 73.0 | 144.5 | 38.6 | 76.7 | ||
| 0.600 1 | 70.7 | 141.4 | 34.9 | 69.8 | 18.6 | 37.2 | ||
| 0.700 1 | 38.5 | 76.3 | 18.8 | 37.6 | 10.0 | 20.0 | ||
| 0.800 1 | 22.1 | 44.7 | 11.0 | 22.1 | 5.8 | 11.7 | ||
| 0.900 2 | 14.0 | 27.9 | 7.0 | 13.8 | 3.7 | 7.3 | ||
在实际应用中,通过切换伽利略式望远镜扩束系统中凹透镜的方式调整激光光束发散角,系统中两透镜处于共焦状态,离焦量Δl为0,离焦像差为0,不存在离焦像差。当无离焦像差时,假设探测目标与测距台站的距离R为500~1 600 km,探测目标参数同上。探测器的光敏面产生光电子的概率服从泊松分布,当回波光子数为n时,至少产生一个光电子的概率为[14]
| $ P(\geqslant 1)=1-\mathrm{e}^{-n}, $ | (23) |
(23) 式也称为探测成功概率。
由(22)式和(23) 式可以计算目标探测成功概率。结果见表 5,表头行数据表示角放大率,表头列数据表示探测目标与测距台站间的距离,单位为km。由表 5可知,当角放大率为0.10~0.50时,探测成功概率均为100%。但是,探测成功概率受很多因素影响,例如望远镜的跟踪精度、激光能量波动和大气湍流等,实际情况和理论结果有差别。测距系统的发射激光光束直径为15 mm,望远镜副镜有效通光口径为48 mm。为充分利用望远镜口径,光束的最大扩束倍率为副镜有效通光口径与光束直径之比3.2,即角放大率为0.31,因此扩束系统的角放大率最好不小于0.31 (扩束倍率与角放大率成反比)。综合以上分析,针对探测距离为500~1 600 km的目标,扩束系统的角放大率为0.3,0.4和0.5。
| Distance/km | Angle magnification | ||||||||
| 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | |
| 500 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 600 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 |
| 700 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.95 |
| 800 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 0.90 |
| 900 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.94 | 0.83 |
| 1 000 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 0.90 | 0.78 |
| 1 100 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.96 | 0.85 | 0.70 |
| 1 200 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.94 | 0.80 | 0.63 |
| 1 300 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.91 | 0.75 | 0.59 |
| 1 400 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 0.86 | 0.70 | 0.55 |
| 1 500 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.96 | 0.83 | 0.63 | 0.50 |
| 1 600 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.94 | 0.80 | 0.59 | 0.45 |
本文通过理论分析,研究了离焦像差对光束能量密度分布和激光测距回波光子数的影响。数值仿真结果表明,离焦像差使光斑形状变得弥散,降低目标接收的能量,影响测距系统接收的回波光子数。对于不同距离的同一颗卫星,在不同角放大率下,无离焦像差时测距系统接收的回波光子数约是有焦像差时的2倍。由表 1可知,通过改变扩束系统中两透镜间距离来调整发散角,离焦量越大,离焦像差的波前均方根越大,严重影响光束的能量密度分布。对于不同距离的同一颗卫星,在不同角放大率下,无离焦像差时测距系统接收的回波光子数约是有焦像差时的2倍。因此,无离焦像差可以有效提高测距系统探测成功的概率。
| [1] |
李语强, 伏红林, 李荣旺, 等. 云南天文台月球激光测距研究与实验[J]. 中国激光, 2019, 46(1): 0104004 LI Y Q, FU H L, LI R W, et al. Research and experiment of lunar laser ranging in Yunnan Observatories[J]. Chinese Journal of Lasers, 2019, 46(1): 0104004. |
| [2] |
项清革, 卫志斌, 程伯辉, 等. 卫星激光测距仪发散角系统的设计[J]. 测绘科学, 2004, 29(5): 44–46 XIANG Q G, WEI Z B, CHENG B H, et al. Laser divergence designing for satellite laser ranging[J]. Science of Surveying and Mapping, 2004, 29(5): 44–46. DOI: 10.3771/j.issn.1009-2307.2004.05.012 |
| [3] |
鲜浩, 姜文汉. 波像差与光束质量指标的关系[J]. 中国激光, 1999, 26(5): 32–36 XIAN H, JIANG W H. The relation between wavefront aberration and the beam quality factor[J]. Chinese Journal of Lasers, 1999, 26(5): 32–36. |
| [4] |
季小玲, 陶向阳, 吕百达. 光束控制系统热效应与球差对激光光束质量的影响[J]. 物理学报, 2004, 53(3): 952–960 JI X L, TAO X Y, LYU B D. The influence of thermal effects in a beam control system and spherical aberration on the laser beam quality[J]. Acta Physica Sinica, 2004, 53(3): 952–960. DOI: 10.3321/j.issn:1000-3290.2004.03.057 |
| [5] |
李新阳, 鲜浩, 王春鸿, 等. 波像差与光束质量β因子的关系[J]. 中国激光, 2005, 32(6): 798–802 LI X Y, XIAN H, WANG C H, et al. Relationship between beam quality factor β and wavefront error[J]. Chinese Journal of Lasers, 2005, 32(6): 798–802. DOI: 10.3321/j.issn:0258-7025.2005.06.016 |
| [6] |
郁道银, 谈恒英. 工程光学[M]. 4版. 北京: 机械工业出版社, 2016: 179-181. YU D Y, TAN H Y. Engineering optics[M]. 4th ed. Beijing: China Machine Press, 2016: 179-181. |
| [7] |
吕百达. 激光光学: 激光束的传输变换和光束质量控制[M]. 3版. 成都: 四川大学出版社, 1992: 98-145. LYU B D. Laser optics: transmission transformation and beam quality control of laser beam[M]. 3rd ed. Chengdu: Sichuan University Press, 1992: 98-145. |
| [8] |
李俊昌. 激光的衍射及热作用计算[M]. 北京: 科学出版社, 2002: 220-222. LI J C. Calculation of laser diffraction and thermal interaction[M]. Beijing: Science Press, 2002: 220-222. |
| [9] | 史广维. 基于矢量波像差理论的反射望远系统装调研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2011: 27-33. SHI G W. Research on the installation and adjustment of reflective telescope system based on vector wave aberration theory[D]. Changchun: Changchun Institute of Optics, Precision Machinery and Physics, Chinese Academy of Sciences, 2011: 27-33. |
| [10] |
于学刚, 刘忠, 金振宇, 等. 波前相位差法探测器的设计[J]. 天文研究与技术, 2010, 7(1): 55–59 YU X G, LIU Z, JIN Z Y, et al. Design of a phase diverstiy wavefront sensor[J]. Astronomical Research & Technology, 2010, 7(1): 55–59. |
| [11] | 熊耀恒. 月球激光测距的新技术方法研究[D]. 昆明: 中国科学院云南天文台, 2001: 6-8. XIONG Y H. Research on new technology of lunar laser ranging[D]. Kunming: Yunnan Observatories, Chinese Academy of Sciences, 2001: 6-8. |
| [12] | 伏红林. 激光测距中激光性质的研究及其在实测中的应用[D]. 昆明: 中国科学院云南天文台, 2003: 5-6. FU H L. Study of laser properties in laser ranging and its application in measurement[D]. Kunming: Yunnan Observatories, Chinese Academy of Sciences, 2003: 5-6. |
| [13] |
万凡, 汤儒峰, 翟东升, 等. 激光光斑特性测量方法研究[J]. 天文研究与技术, 2020, 17(4): 463–470 WAN F, TANG R F, ZHAI D S, et al. Research on measurement method of laser spot characteristics[J]. Astronomical Research & Technology, 2020, 17(4): 463–470. DOI: 10.3969/j.issn.1672-7673.2020.04.008 |
| [14] |
高清鹏, 李春晓, 李荣旺, 等. 鹊桥卫星激光测距时间窗口及测距成功概率分析[J]. 天文研究与技术, 2019, 16(4): 422–430 GAO Q P, LI C X, LI R W, et al. Magpie bridge satellite laser ranging time window and distance probability analysis[J]. Astronomical Research & Technology, 2019, 16(4): 422–430. DOI: 10.3969/j.issn.1672-7673.2019.04.005 |



