2. 中国科学院大学, 北京 100049;
3. 中国科学院射电天文重点实验室, 江苏 南京 210033;
4. 国家基础学科公共科学数据中心, 北京 100190;
5. 上海市导航定位重点实验室, 上海 200030
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
4. National Public Science Data Center for Basic Disciplines, Beijing 100190, China;
5. Shanghai Key Laboratory of Space Navigation and Positioning Techniques, Shanghai 200030, China
地球同步轨道卫星的轨道高度约36 000 km,绕地公转周期与地球自转周期一致,一定范围内相对地面点静止,在大地测量、导航定位和灾害监测等方面发挥重要作用。由于地球同步轨道卫星运动时受各种摄动力影响,特别是太阳能翼板受到的太阳光压摄动大,卫星的实际轨道发生漂移,偏离平衡点[1]。为减少轨道误差的影响,需尽快获取卫星准确的位置信息,因此研究地球同步轨道卫星机动后的位置快速测量方法具有重要意义。
目前对地球同步轨道卫星视向位置测量主要依靠测距技术,包括伪距和载波相位测量、转发式测距测量和激光测距等。高精度测距需要卫星转发测距信号,为主动式测量,定轨精度百米量级[2]。制约测距定轨精度的因素与地球同步轨道卫星的特点有关:卫星轨道高,地面跟踪站构网范围相对较小,导致观测网几何结构略差;相对静止特性使得星站间动力学和几何约束变弱,造成钟差和测站偏差等系统误差解算困难;为维持同步轨道,卫星需频繁轨道控制,但星上发动机推力不易建模,造成后续轨道恢复和预测困难[2-4]。
对地球同步轨道卫星的轨道平面位置测量可以采用光学成像或射电干涉等被动式测量方法,这些方法的优点为仅需要接收卫星下行信息,不占用星上资源。拥有独立本振的甚长基线干涉测量技术是一种射电干涉测量技术,因具有超高测角分辨率和灵敏度,已广泛应用于深空探测器跟踪测量[5]。甚长基线干涉测量对确定卫星横向(垂直于卫星轨道径向平面) 位置具有高灵敏度,可以提供观测目标角位置的几何约束。差分甚长基线干涉测量技术通过快速交替观测目标探测器和邻近致密射电源,利用信号差分可以有效减少介质时延、仪器时延、测站钟差等测量误差,测角精度优于毫角秒[6-7]。
联合使用甚长基线干涉测量技术与测距技术可以进一步提高地球同步轨道卫星的三维位置解算精度。1984年,文[8]采用差分甚长基线干涉测量技术与无线电测距对地球同步轨道卫星进行联合定轨试验,得到卫星轨道精度约100 m。近年来国内学者也开展了对地球同步轨道卫星的仿真试验和实测研究。2003年,文[9]利用双差分单程测距(Delta Differential One-way Ranging, ΔDOR) 和双差单向测速两种差分甚长基线干涉测量技术,开展我国首次地球同步轨道卫星的甚长基线干涉测量实测试验,获得卫星信号的干涉条纹,未进行实际卫星定位定轨计算。试验的双差单向测距总误差约41 cm,理论上相当于用2 000 km基线观测地球同步轨道目标时8 m的位置误差。2006年,文[3]的数值仿真试验表明,在测距观测中增加甚长基线干涉测量辅助观测数据,理论上有望将地球同步轨道卫星的轨道精度提高至米级,但未开展实测试验。2011年,文[2]利用C波段转发式测距数据和时延数据进行综合定轨试验,定轨后时延数据残差均方根值约3.6 ns,时延率约0.4 ps/s,相当于轨道横向位置误差约10 m。2017年,文[10]利用宽带甚长基线干涉测量系统与轨道跟踪和转移测定系统观测地球同步轨道卫星,得到约0.14 ns的时延形式误差,同一时段重复定轨结果的中误差在米级[10]。前述试验结果均未与观测目标事后精密轨道比较,准确度暂无法衡量。
卫星轨道控制后轨道的恢复时间长、偏差大,且地球同步轨道卫星定轨精度的要求越来越高,因此,研究地球同步轨道卫星位置的快速高精度测量技术,具有重要现实意义。我们组织中国VLBI网所属4个台站观测地球同步轨道卫星,并利用甚长基线干涉测量短时观测的时延测量数据对地球同步轨道卫星进行定位计算。中国VLBI网由天马(Tm)、北京(Bj)、昆明(Km)、乌鲁木齐(Ur) 4个观测站和位于上海的数据处理中心组成,含6条观测基线。本文首先从理论上对地球同步轨道卫星时延观测精度进行分析,然后利用约4 h的S波段时延数据进行卫星定位计算。同时文中详细描述了时延结果中的异常值检测和校正方法,并利用校正后的时延数据和新开发的后处理程序重新进行地球同步轨道卫星定位计算,通过定位结果验证时延跳变的校正效果。计算结果与国际全球导航卫星系统服务组织(International Global Navigation Satellite Systems Service, IGS) 提供的事后精密轨道数据进行比较,可以作为定位结果的外符合准确度估计。
1 卫星差分甚长基线干涉测量原理与精度分析 1.1 卫星差分甚长基线干涉测量原理甚长基线干涉测量的观测量为时延和时延率,即两个地面天线接收同一信号的时间延迟和时间延迟变化率,包括群时延(率)和相时延(率)。差分甚长基线干涉测量技术即选取目标探测器附近位置精确已知的致密射电源作为参考源,交替观测参考源和目标探测器。一般要求两者角距小于10 °[11],观测频率越高,可用的角距范围越大。通过两信号差分,可以有效减少时延测量误差。差分甚长基线干涉测量原理示意图如图 1。图中1和2为两观测台站;B为两台站组成的基线矢量;r为台站观测射电源方向矢量;r1和r2为台站观测卫星方向矢量;τ为射电源观测时延。
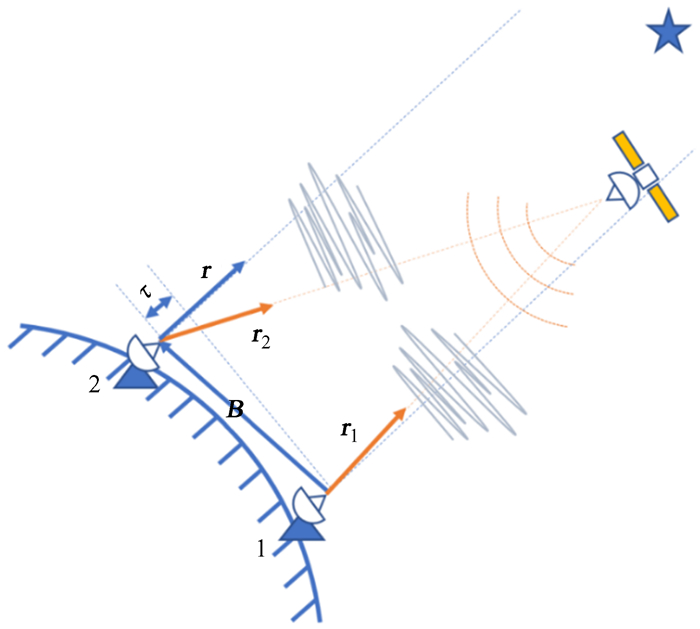
|
| 图 1 差分甚长基线干涉测量原理示意图 Fig. 1 Schematic diagram of differential VLBI principle |
测量时,按照参考源-目标卫星-参考源的顺序,在t1,t2和t3时刻对应的时延值分别为τq(t1),τs(t2)和τq(t3),上标q表示参考源观测,s表示卫星观测。通过插值可以得到t2时刻参考源观测量τq(t2)。在t2时刻,有如下关系
| $ \tau^{\mathrm{q}}\left(t_{2}\right)=\tau_{\mathrm{g}}^{\mathrm{q}}\left(t_{2}\right)+\tau_{\mathrm{err}}^{\mathrm{q}}\left(t_{2}\right), $ | (1) |
| $ \tau^{s}\left(t_{2}\right)=\tau_{\mathrm{g}}^{\mathrm{s}}\left(t_{2}\right)+\tau_{\mathrm{err}}^{\mathrm{s}}\left(t_{2}\right), $ | (2) |
其中,τg为几何时延,由台站坐标、观测源坐标和地球定向参数等先验值计算得到;τerr为观测中的系统误差和随机误差之和,包括介质时延、钟差、仪器时延和观测噪声等。差分甚长基线干涉测量时延观测值为
| $ \Delta \tau=\tau^{\mathrm{s}}\left(t_{2}\right)-\tau^{\mathrm{q}}\left(t_{2}\right)=\tau_{\mathrm{g}}^{\mathrm{s}}\left(t_{2}\right)-\tau_{\mathrm{g}}^{\mathrm{q}}\left(t_{2}\right)+\varepsilon_{\tau}, $ | (3) |
| $ \varepsilon_{\tau}=\tau_{\text {err }}^{\mathrm{s}}\left(t_{2}\right)-\tau_{\mathrm{err}}^{\mathrm{q}}\left(t_{2}\right) . $ | (4) |
因τerrs(t2) 和τerrq(t2) 为同一时刻观测误差值,可以认为钟差和仪器时延等近似相等,又因观测间隔时间短且参考源和目标探测器角距近,所以介质时延相差小。因此,差分得到的ετ为极小误差项,消除了观测中无法精确建模的共同误差源影响,得到卫星的实际甚长基线干涉测量时延值
| $ \tau^{\mathrm{s}}\left(t_{2}\right) \approx \tau^{\mathrm{q}}\left(t_{2}\right)+\Delta \tau, $ | (5) |
τs(t2) 包含卫星的位置信息,可以用于定位。
1.2 时延精度与卫星位置误差分析为评估卫星位置解算精度,我们需要对甚长基线干涉测量精度进行理论分析。时延测量误差主要包括射电源位置、台站位置、地球定向参数和介质等带来的系统性误差,以及观测源噪声、氢原子钟不稳定度、介质扰动和仪器相位抖动等带来的随机误差[12]。
1.2.1 射电源位置误差甚长基线干涉测量时从国际天球参考架优先选择位置精度高的点源,因此系统误差中的源位置时延误差是一个与源本身位置精度和投影基线有关的极小量,估算公式为[12]
| $ {\varepsilon _{\Delta \tau }} = \frac{{{B_{\rm{p}}}}}{c}{\varepsilon _\vartheta }, $ | (6) |
其中,Bp为基线在天空平面投影的长度;εϑ为河外源位置误差;c为光速。大部分源的位置精度为0.5~2.0 nrad,对投影长度3 000 km的基线,射电源位置误差0.75 nrad时,由射电源位置误差带来的时延误差约为0.007 5 ns。
1.2.2 台站位置误差台站位置时延误差可以用基线在天球面的投影误差表示,与射电源和卫星夹角有关,可以表示为[12]
| $ \varepsilon_{\Delta \tau}=\frac{1}{c}(\Delta \theta) \varepsilon_{\mathrm{BL}}, $ | (7) |
其中,Δθ为射电源和卫星夹角;εBL为基线投影误差。假定射电源和卫星夹角0.2 rad,基线投影误差0.02 m,则由台站位置误差带来的时延误差约为0.013 3 ns。
1.2.3 地球定向参数误差地球定向参数对时延的影响主要由模型计算时的坐标系转换引入,取决于UT1和极移参数的精度,与卫星和参考源间的夹角成比例,关系为[12]
| $ \varepsilon_{\Delta \tau}=\frac{1}{c}(\Delta \theta) \varepsilon_{\mathrm{UTPM}}, $ | (8) |
其中,εUTPM为地球定向参数UT1和极移引起的基线的误差,为一极小值。假定射电源和卫星夹角0.2 rad,地球定向参数为0.02 m,则由其产生的时延误差约为0.013 3 ns。
1.2.4 中性大气系统误差中性大气系统误差与台站天顶方向的干湿对流层误差及台站观测目标高度角有关,近似关系为[12]
| $ \varepsilon_{\Delta \tau}=\frac{\rho_{\mathrm{z}}}{c}\left|\frac{1}{\sin \gamma_{\mathrm{s}}+0.015}-\frac{1}{\sin \gamma_{\mathrm{q}}+0.015}\right|, $ | (9) |
其中,γs和γq分别为台站观测卫星和射电源的高度角;ρz为天顶方向的干湿对流层误差。假设卫星高度角40 °,射电源高度角35 °,天顶方向的干对流层误差为0.002 m,天顶方向的湿对流层误差为0.005 m,两个台站干湿对流层影响产生的时延误差约为0.094 9 ns。
1.2.5 电离层系统误差电离层系统性误差对时延误差的影响较复杂,可以由Klobuchar模型的偏导数计算,也可由下式粗略估算[12]
| $ \varepsilon_{\Delta \tau}=\frac{1}{c}\left(\frac{\Delta \theta}{0.1745}\right) \rho_{\text {fluct }}, $ | (10) |
其中,ρfluct为0.2 rad分离角的介质波动不确定性。假设ρfluct为0.03 m,则带来的电离层系统误差为0.114 7 ns。若观测台站周围布设有双频GPS接收机可以获得更准确的台站天空电离层信息。
1.2.6 卫星热噪声误差地球同步轨道卫星热噪声与卫星信号信噪比、观测通道带宽和积分时间等有关,近似关系为[12]
| $ {\varepsilon _{\Delta \tau }} = \frac{{\sqrt {12} }}{{2\pi \Delta {f_{{\rm{B}}{{\rm{W}}_{\rm{s}}}}}{R_{{\rm{SN}}}}}}, $ | (11) |
其中,ΔfBWs为卫星观测带宽;RSN为卫星信号信噪比。地球同步轨道卫星数传信号通常为带宽10 MHz的单通道观测,假定卫星信噪比为1 000,则卫星热噪声带来的时延误差约0.055 1 ns。
1.2.7 河外射电源热噪声误差河外射电源通常为多通道观测,其热噪声误差与河外射电源信噪比、观测通道带宽和通道数等有关,表示为[12]
| $ \varepsilon_{\Delta \tau}=\frac{1}{2 \pi \Delta f_{\mathrm{BW}_{\mathrm{q}}} R_{\mathrm{SN}_{\mathrm{q}}}}, $ | (12) |
其中,ΔfBWq为河外射电源有效观测带宽;RSNq为河外射电源多通道总信噪比。参考实测中8通道S波段频率设置,得到由河外射电源热噪声引起的时延误差约0.062 1 ns。
1.2.8 台站氢原子钟不稳定度误差氢原子钟不稳定带来的误差具体可以用目标交替观测间隔内的台站钟频率稳定性表示,公式为[12]
| $ \varepsilon_{\Delta \tau}=T_{\mathrm{s}-\mathrm{q}} \varepsilon_{\Delta f / f}, $ | (13) |
其中,Ts-q为射电源和卫星交替观测时间;εΔf/f为氢原子钟的稳定性。若探测器和河外源观测时间间隔为600 s,钟频率稳定度为10-14,则其时延影响为0.006 0 ns。
1.2.9 仪器相位抖动误差仪器相位抖动产生的时延误差与信号总带宽近似成反比,关系为[12]
| $ \varepsilon_{\Delta \tau}=\sqrt{2} \sqrt{2} \frac{\varepsilon_{\varphi}}{360} \frac{1}{f_{\mathrm{BW}_{\mathrm{s}}}}, $ | (14) |
其中,εφ为仪器相位误差;fBWs为总观测带宽。假设仪器相位抖动为0.2 °,总观测带宽为10 MHz,则时延误差为0.078 6 ns。
1.2.10 介质扰动误差对流层和电离层的随机误差与各自观测方向的扰动不确定性及卫星和参考源之间的夹角有关,该项不能通过差分运算消除,由(10) 式近似表示。若对流层和电离层波动不确定性均为0.01 m,则两者对时延影响均为0.038 2 ns。
上述各误差项的统计结果见图 2,图中红色项为系统误差,蓝色项为随机误差,黑色项为所有误差项平方和的平方根值(Root Sum Square, RSS),RSS总误差约0.196 5 ns。
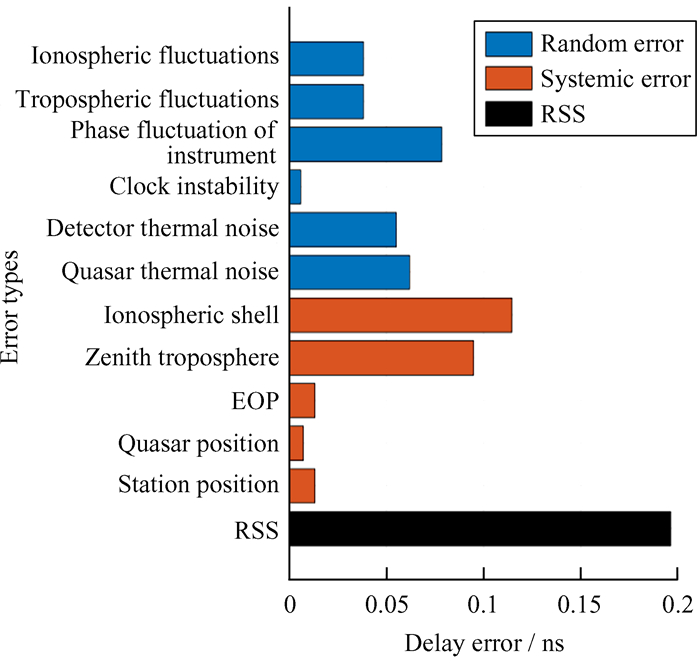
|
| 图 2 时延误差估计 Fig. 2 Estimation of delay error |
差分甚长基线干涉测量的时延测量误差εΔτ与卫星垂直于径向轨道的平面位置误差δε之间满足[2]
| $ \varepsilon_{\Delta \tau}=\frac{\delta_{\varepsilon}}{c} \frac{B}{L}, $ | (15) |
其中,B为基线在天空平面投影的长;L近似认为是测站到卫星的距离。对于地球同步轨道卫星,L约为36 000 km,若投影基线长3 000 km,差分甚长基线干涉测量的时延测量精度在0.072 0 ns时,轨道横向位置精度约为0.71 m。
为了对定位结果的可靠性进行直观评估,我们将试验结果与IGS提供的事后精密轨道数据进行比较。不同机构提供的地球同步精密轨道数据结果本身存在一定差异。目前,德国地球科学研究中心和武汉大学两家机构可以公开提供观测日滞后时间约十几天的地球同步轨道卫星的精密轨道。两机构提供的观测日北斗导航C03星的精密轨道比较结果如图 3。图中横坐标表示观测时刻,纵坐标表示两机构的精密轨道坐标差值。蓝色、橙色、绿色和黑色散点分别为x, y, z坐标分量差和三维坐标差,均方根值依次为1.09 m,0.64 m,0.17 m和1.27 m。三维坐标差最大值约为1.45 m,说明不同机构提供的精密轨道数据本身包含米级的偏差。
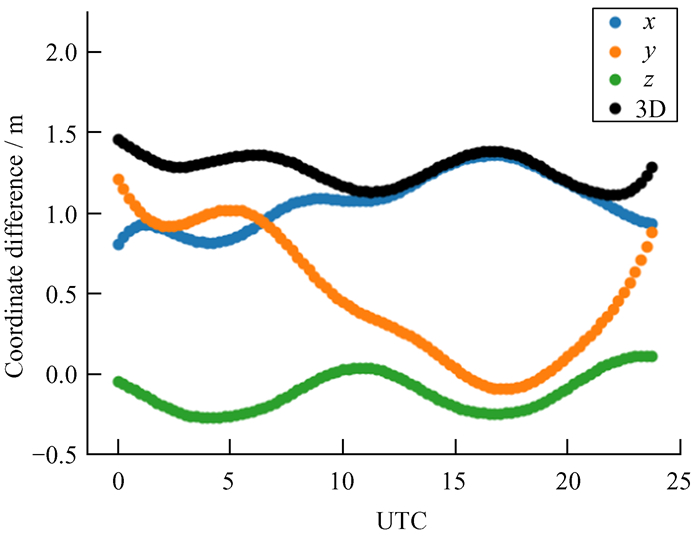
|
| 图 3 德国地球科学研究中心和武汉大学的地球同步轨道卫星精密轨道比较 Fig. 3 Comparison of precise GEO satellite orbit between GFZ and WHU |
我们在世界协调时2018年1月13日进行了一次约4 h的地球同步轨道卫星差分甚长基线干涉测量,信标频率在2.217 GHz,具体观测参数设置见表 1。
| Code | b8113a |
| Observation period | 3:30-7:30 |
| Quasar targets | 1741-038, 1908-201, 2008-1592134+00, 2227-088, 3C454.3 |
| Satellite target | BeiDou C03 |
| Stations | Beijing (Bj), Kunming (Km)Tianma (Tm), Urumqi (Ur) |
| Beacon frequency | S (2.217 GHz) |
| Channels | 8 |
| Bandwidth | 4 MHz |
| Sampling rate | 8 ms/s |
| Quantization bits | 2 bit |
| Data recording format | Mark5B |
中国VLBI网的4台站参与观测,最长基线为东西向的乌鲁木齐- 天马基线(Ur-Tm),长度约3 249 km;最短基线为北京-天马基线(Bj-Tm),长度约1 114 km。由于地球同步轨道卫星的轨道高度较河外射电源低,且相对射电源每小时沿天赤道方向移动15°左右,导致不同测站观测卫星和邻近参考源的视差角不同,且大小随时间变化。为提高观测精度,我们从国际天球参考架中选择6颗邻近C03卫星的致密射电源作为参考源,射电源和卫星天球位置及轨迹如图 4。
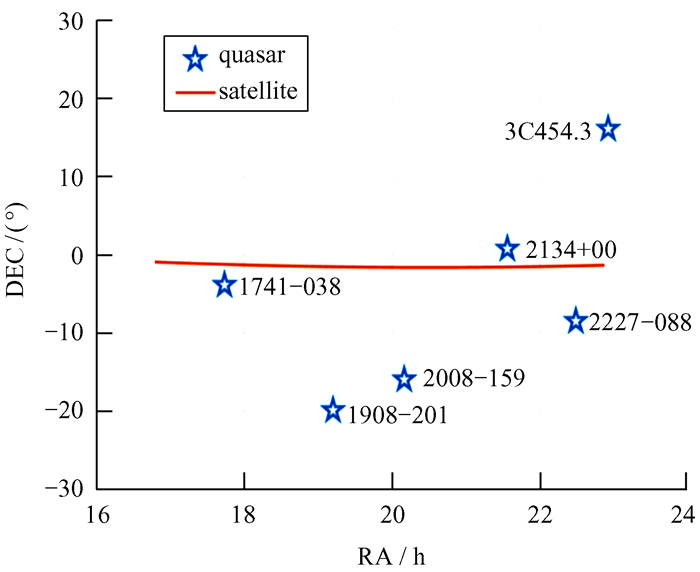
|
| 图 4 射电源和卫星天球位置及轨迹 Fig. 4 Position and trajectory of radio sources and satellites in celestial reference system |
利用中国VLBI网软件相关处理机scorr进行原始观测数据的相关处理后,经校正可以得到观测时延[13]。相关处理利用预先计算的模型时延对两台站接收的两路信号进行补偿,得到残余时延[14]。射电源模型时延为远场模型,卫星模型时延为近场模型,卫星模型时延根据卫星的预报轨道获得,均由上海天文台数据处理中心计算。
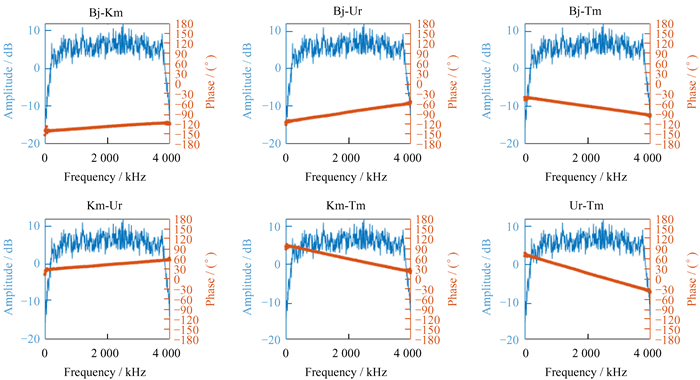
相关处理时傅里叶点数设为1 024,卫星频域512个数据点的互相关功率谱结果如图 5。6个子图分别为北京-昆明基线(Bj-Km)、北京-乌鲁木齐基线(Bj-Ur)、北京-天马基线(Bj-Tm)、昆明-乌鲁木齐基线(Km-Ur)、昆明-天马基线(Km-Tm)和乌鲁木齐-天马基线(Ur-Tm) 的结果。图中横坐标为频率,单位kHz;纵坐标蓝色为幅度谱,单位dB,橙色为相位谱,单位为度(°)。从相关处理结果可以看出,6条基线均获得较好的干涉条纹。
|
| 图 5 6条基线互相关功率谱 Fig. 5 Cross-correlation power spectrum of 6 baselines |
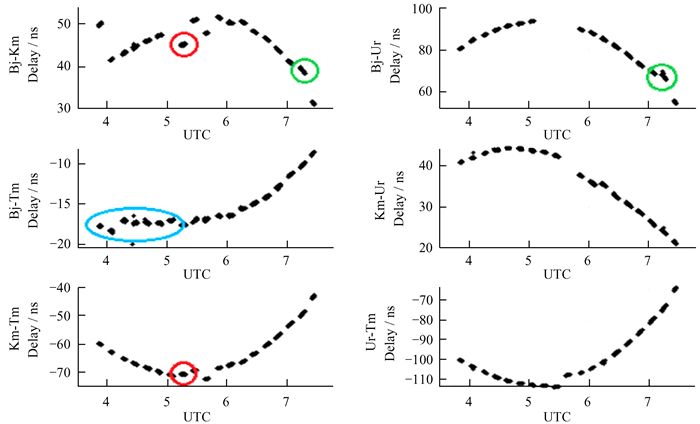
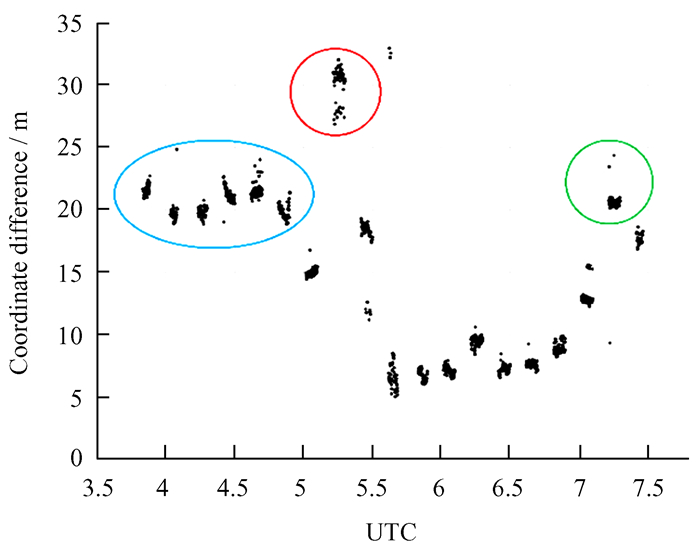
相关处理后的时延数据进行拟合、钟差改正及介质改正等,结果如图 6,横坐标为观测时刻,纵坐标为6条基线的残余时延值,单位ns。6条基线残余时延拟合后残差中误差分别为2.35 ns,1.15 ns,0.39 ns,0.75 ns,0.70 ns和0.86 ns,均值为1.03 ns。图上显示部分时段的残余时延结果存在缺值和跳变情况。残余时延缺值的原因考虑为观测时台站的数据记录缺失,产生跳变的原因较复杂,将在2.3节进一步分析。残余时延与模型时延的和为总时延,因甚长基线干涉测量对确定卫星径向位置不敏感,若仅利用总时延数据解算卫星位置,解算结果精度较差,因此可以采用距离约束的方法。假定卫星的地心距等于预报轨道计算的地心距,则地心距约束的先验误差由预报轨道误差给定[15]。将该等式与甚长基线干涉测量观测等式共同组成误差方程解算卫星位置,并与IGS提供的精密轨道数据进行比较,三维坐标差结果如图 7。两者坐标差小于35 m,坐标均方根误差约16.76 m。图 7中部分时段卫星定位结果存在跳变,与残余时延结果图中存在跳变的时段较一致,对应时段数据分别在两图中由蓝色、红色和绿色线圈标出。
|
| 图 6 6条基线残余时延 Fig. 6 Residual delay of 6 baselines |
|
| 图 7 卫星坐标差 Fig. 7 Satellite coordinate difference |
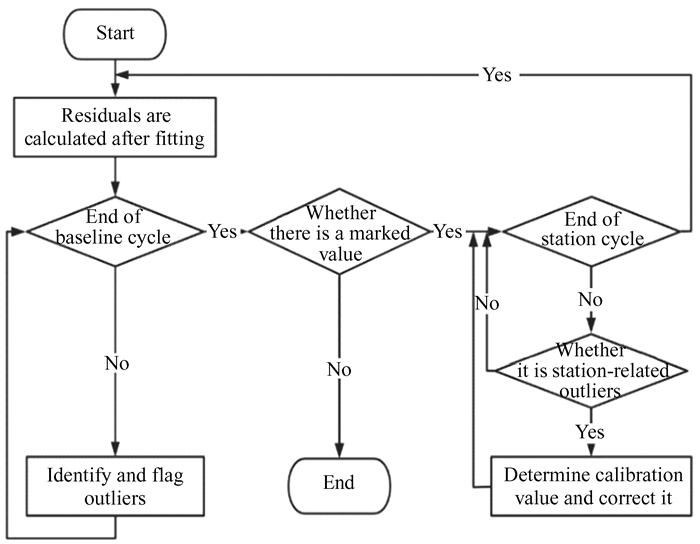
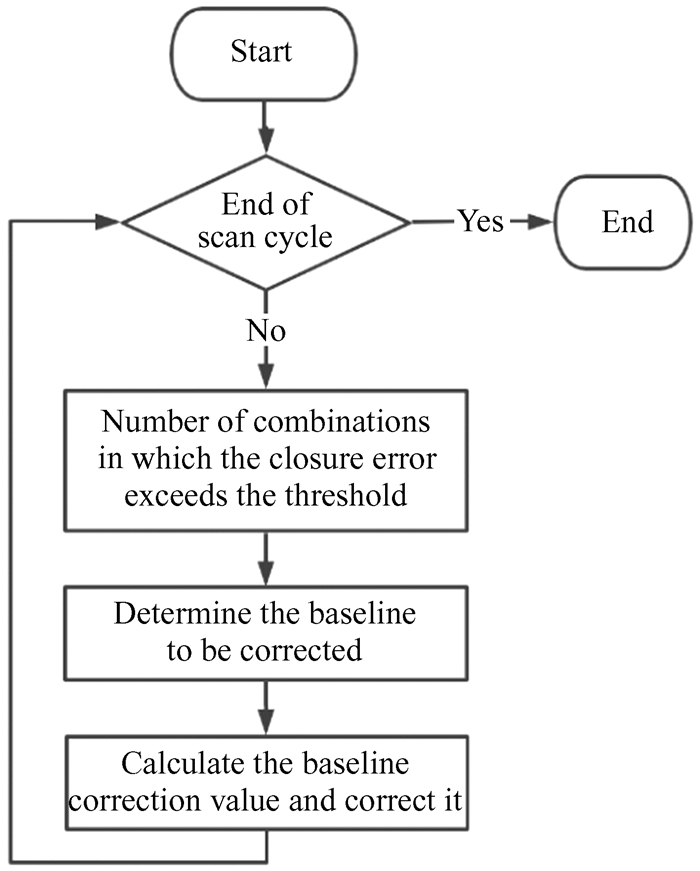
时延异常直接影响卫星最终的定位结果。为提高卫星位置解算精度,我们需要对残余时延数据异常值进行检测和校正,改正残余时延跳变问题。时延异常产生的主要原因分两类:(1) 与台站相关,如台站测量记录设备引入的误差或钟差修正残余部分;(2) 与基线相关,由数据处理误差引入。因残余时延数据为时间序列数据,异常检测时不能作为孤立的样本点处理,我们借助多项式拟合的方法和基线理论时延闭合差为零的约束条件来检测两类异常值。将每条基线的残余时延拟合值残差作为异常值检测数据,偏离平均值一定倍数标准差的数据即为异常值。与台站和基线相关的异常值检测校正方法流程图分别见图 8和图 9,主要步骤包括(1) 确定标记异常值;(2) 判断是否台站、基线相关;(3) 计算校正值并校正。
|
| 图 8 台站异常值检测校正流程 Fig. 8 Outlier detection and correction flow of stations |
|
| 图 9 基线异常值检测校正流程 Fig. 9 Outlier detection and correction flow of baselines |
首先检测台站相关异常值,试验中采用拟合值残差1倍标准差作为异常值检测阈值,若同一时段与某一台站相关的所有基线均标记有异常值,则认为该时段存在台站相关的数据异常。在确定为台站相关异常值后,对异常时段的台站数据进行校正:在0到最大异常偏离值范围内,每隔一较小间隔确定一改正值,计算改正后所有基线的时延测量值与拟合值差值平方和,最终的改正值应使该平方和最小。
针对基线数据处理引入的误差,误差检测与校正方法主要基于多基线理论时延闭合差为0的条件,4个台站6条基线共4种组合方式,如用BK-KU-BU表示Bj-Km、Km-Ur和Bj-Ur基线组合。计算不同基线组合的时延闭合差,求每个扫描周期内每一时延闭合差的平均值(以下称闭合差均值)。设阈值为1.25 ns,闭合差均值超阈值处为需要校正的时段,取闭合差均值绝对值的基线组合闭合差的平均值为校正值。正负号根据闭合差均值正负和该基线在组合中的位置判断,例如:在某一扫描周期内,BK-KU-BU和BK-KT-BT基线组合同时被标记,则共同基线BK (即Bj-Km基线) 需要校正;若该扫描周期内BK-KU-BU和BK-KT-BT基线组合闭合差均值都为正,则BK基线需减去改正值,反之需加上改正值。台站记录数据缺失会导致基线数据空缺,受部分时段数据空缺和不同基线组合闭合差较大等影响,可能导致无法确定需校正的具体基线,可以通过修改闭合差阈值的大小来综合判断。
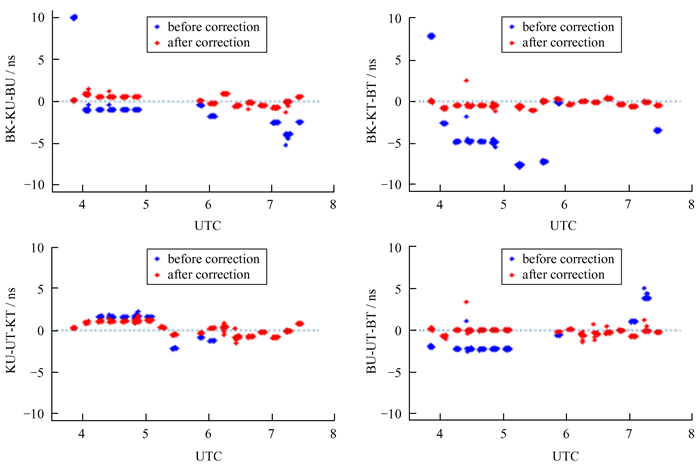
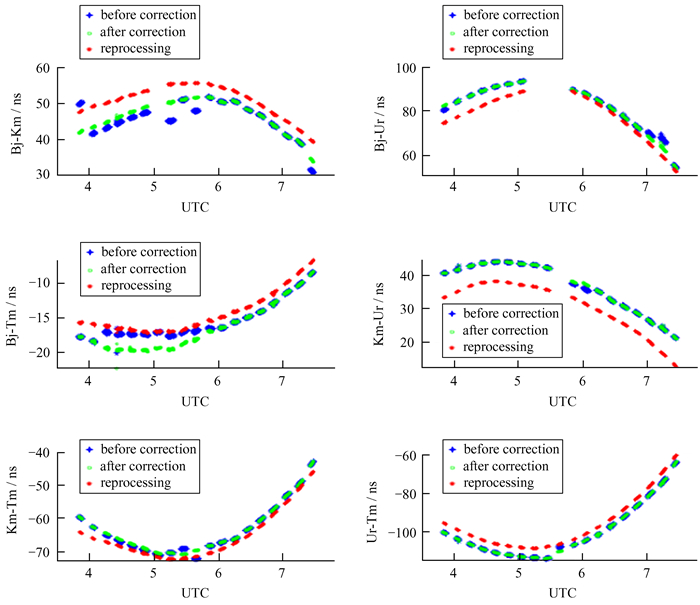
校正前后的基线组合时延闭合差对比如图 10,横坐标为观测时刻,纵坐标为基线组合的时延闭合差,单位ns。蓝色散点为校正前的时延闭合差,部分时段闭合差结果较差;红色散点为经台站和基线异常值校正后的闭合差结果,校正后的结果更接近理论零值。校正前后的残余时延分别为图 11中蓝色星号和绿色圆圈,从图中对比可以看出,残余时延经过校正后变平滑。校正后的6条基线残余时延拟合后残差中误差分别为0.56 ns,0.53 ns,0.31 ns,0.66 ns,0.50 ns和0.70 ns,均值为0.54 ns。
|
| 图 10 基线组合闭合差校正前后结果比较 Fig. 10 Comparison of baseline combination closure error before and after correction |
|
| 图 11 校正前后与重新处理后的6条基线残余时延对比 Fig. 11 Comparison of residual delay of 6 baselines before and after correction and reprocessing |
为进一步提高卫星的定位精度,对数据重新处理后,残余时延数据变得更加平滑,见图 11中的红色线。采用五阶多项式拟合残余时延数据,时延精度用拟合后残差中误差表示,最终得到6条基线时延拟合后的残差中误差分别为0.16 ns,0.23 ns,0.14 ns,0.14 ns,0.14 ns和0.13 ns,均值为0.16 ns,等效于轨道横向位置误差约0.58 m。
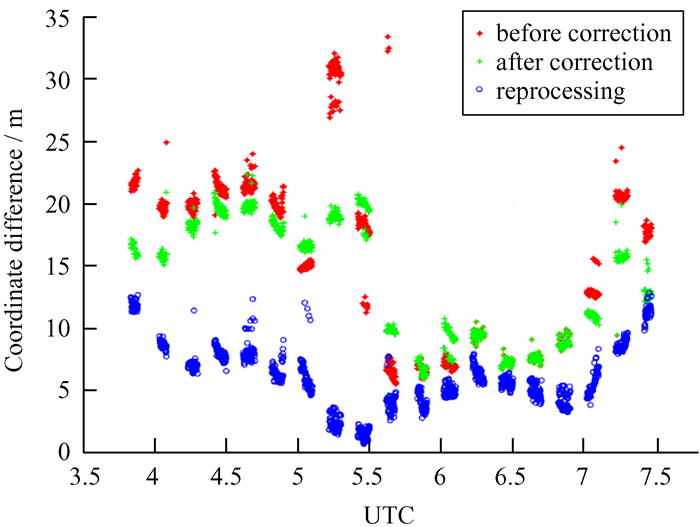
我们分别用校正后和重新处理的总时延数据对地球同步轨道卫星定位计算。定位结果与精密轨道坐标差的比较见图 12。红色星号为校正前的结果,绿色加号为校正后的结果,蓝色圆圈为新处理程序的结果。经过基线和台站时延校正后,卫星定位精度有一定提高,尤其是图 6中标出的3处存在异常值的时段,用新的后处理程序重新处理后的轨道定位结果与精密轨道比较,均方根误差约6.61 m,3次处理结果的残余时延残差均值和卫星坐标均方根误差统计见表 2。
|
| 图 12 卫星坐标差对比 Fig. 12 Comparison of satellite coordinate differences |
| Before correction | After correction | Reprocessing | |
| Mean of residual delay/ns | 1.03 | 0.54 | 0.16 |
| RMS of coordinate difference/m | 16.76 | 14.59 | 6.61 |
试验结果表明,利用仅4 h的短时甚长基线干涉测量时延数据可以得到外符合精度米级的地球同步轨道卫星定位结果,有利于地球同步轨道卫星的快速轨道恢复。本次实测试验结果与历史实测结果对比见表 3,对比表明,此次甚长基线干涉测量窄带观测时延测量精度较历史窄带观测结果有较大提高,且接近宽带观测的时延精度结果。并且本文首次计算了外符合精度结果,更好地评估定位结果的准确度。虽然与精密轨道结果相比仍有一定差异,但在地球同步轨道卫星轨道控制后可以快速提供较高精度的卫星位置信息,减少轨道误差影响,仍具有重要意义。
| Year | VLBI observation mode | VLBI observation accuracy | estimated horizontal position accuracy/m | external coincidence accuracy/m |
| 1984 | 17 hours, 4 GHz | 2 ns | / | / |
| 2003 | 3 hours, 2/8 GHz, 4 M bandwidth | ΔDOR 41 cm | 8 | / |
| 2011 | 3 hours, 2 GHz, 2 M bandwidth | 3.6 ns | 10 | / |
| 2017 | 36 hours, 4 GHz, 32 M bandwidth | 0.14 ns | 0.42 | / |
| our article | 4 hours, 2 GHz, 4 M bandwidth | 0.16 ns | 0.58 | 6.61 |
利用甚长基线干涉测量技术观测地球同步轨道卫星,可以充分发挥甚长基线干涉测量对卫星横向位置约束精度高的特点,提高地球同步轨道卫星的短时定位精度,有利于卫星机动后的轨道快速恢复。本文首先对甚长基线干涉测量时延进行理论精度分析,包括射电源位置、台站位置、地球自转参数和介质等带来的系统误差,以及观测源噪声、氢原子钟不稳定度、介质扰动和仪器相位抖动等带来的随机误差。分析得到差分甚长基线干涉测量时延理论测量精度为0.196 5 ns,换算为卫星平面位置误差约0.71 m。
实测试验利用中国VLBI网的4个台站观测地球同步轨道卫星,得到4 h的甚长基线干涉测量残余时延数据的拟合后残差中误差均值为1.03 ns。结果显示残余时延存在缺值和跳变的情况,影响时延测量精度。因此本文提出了针对该情况的异常值检测校正方法,分别考虑与观测台站和观测基线相关的异常值校正。重新处理校正后的数据得到残余时延拟合后残差中误差均值为0.16 ns。进而进行卫星定位计算验证该时延异常值的校正效果,发现卫星定位结果与IGS提供的精密轨道结果差异由16.76 m提高到6.61 m,说明了校正方法的有效性。本文的研究可以利用短时甚长基线干涉测量观测数据进行地球同步轨道卫星的快速高精度定位,有望用于地球同步轨道卫星轨道的快速恢复。
在此基础上,未来我们可以利用时延观测数据和时延率数据预报短时间的甚长基线干涉测量时延值,并进行后续地球同步轨道卫星位置预报的相关研究。随着甚长基线干涉测量全球观测系统的不断完善,将会有更多台站和更多基线组合可以用于地球同步轨道卫星的跟踪观测。另外通过设置专门的差分单程测距信标或宽带信标等方式,进一步提高短时测量精度,提高地球同步轨道卫星的轨道监测能力。
| [1] |
刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000: 211-451. LIU L. Orbit theory of spacecraft[M]. Beijing: National Defense Industry Press, 2000: 211-451. |
| [2] |
黄勇, 胡小工, 张秀忠, 等. VLBI应用于GEO导航卫星的测定轨[J]. 科学通报, 2011, 56(24): 1974–1981 HUANG Y, HU X G, ZHANG X Z, et al. Improvement of orbit determination for geostationary satellites with VLBI tracking[J]. Chinese Science Bulletin, 2011, 56(24): 1974–1981. |
| [3] |
杜兰, 郑勇, 李杰. VLBI在GEO卫星精密定轨中的应用[J]. 测绘科学技术学报, 2006, 23(4): 269–271 DU L, ZHENG Y, LI J. VLBI-augmented orbit determination for geostationary satellites[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(4): 269–271. DOI: 10.3969/j.issn.1673-6338.2006.04.010 |
| [4] |
杨旭海, 李志刚, 冯初刚, 等. GEO卫星机动后的星历快速恢复方法[J]. 中国科学: 物理学力学天文学, 2008(12): 1759–1765 YANG X H, LI Z G, FENG C G, et al. Rapid recovery method of ephemeris after maneuver of GEO satellite[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2008(12): 1759–1765. |
| [5] |
李金岭, 张津维, 刘鹂, 等. 应用于深空探测的VLBI技术[J]. 航天器工程, 2021, 21(2): 62–67 LI J L, ZHANG J W, LIU L, et al. VLBI technique applied in deep space exploration[J]. Spacecraft Engineering, 2021, 21(2): 62–67. |
| [6] |
童锋贤, 郑为民, 舒逢春. VLBI相位参考成像方法用于玉兔巡视器精确定位[J]. 科学通报, 2014, 59(34): 3362–3369 TONG F X, ZHENG W M, SHU F C. Accurate relative positioning of Yutu lunar rover using VLBI phase-referencing mapping technology[J]. Chinese Science Bulletin, 2014, 59(34): 3362–3369. |
| [7] |
聂振华, 张波, 乔书波, 等. 深空探测器的VLBI逆相位参考定位[J]. 中国科学: 物理学力学天文学, 2017, 47(12): 102–110 NIE Z H, ZHANG B, QIAO S B, et al. Positioning of spacecraft with VLBI inverse phase reference[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2017, 47(12): 102–110. |
| [8] | SHIOMI T, KOZONO S I, ARIMOTO Y, et al. Precise orbit determination of a geosynchronous satellite by Delta VLBI method[J]. Journal of the Radio Research Laboratory, 1984, 31(133): 111–132. |
| [9] |
舒逢春, 张秀忠, 郑为民. 地球同步卫星的VLBI观测[J]. 中国科学院上海天文台年刊, 2003(1): 105–111 SHU F C, ZHANG X Z, ZHENG W M. VLBI observations of geosynchronous satellites[J]. Annals of Shanghai Observatory Academia Sinica, 2003(1): 105–111. |
| [10] | GONG J J, CAO F, YANG X, et al. The GEO satellite orbit experiment measured by combination of the broadband VLBI & the orbit tracking of two way range[J]. Boletin Tecnico/Technical Bulletin, 2017, 55(8): 39–47. |
| [11] |
钱志瀚, 李金岭. 甚长基线干涉测量技术在深空探测中的应用[M]. 北京: 中国科学技术出版社, 2010. QIAN Z H, LI J L. The application of very long baseline interferometry in deep space navigation[M]. Beijing: China Science and Technology Press, 2010. |
| [12] | Delta-DOR-technical characteristics and performance: informational report: CCSDS 500.1-G-2[R]. Washington: Management Council of the Consultative Committee for Space Data Systems (CCSDS), 2019. |
| [13] |
郑为民, 舒逢春, 张冬. 应用于深空跟踪测量的VLBI软件相关处理技术[J]. 宇航学报, 2008, 29(1): 18–23 ZHENG W M, SHU F C, ZHANG D. Application of software correlator to deep space VLBI tracking[J]. Journal of Astronautics, 2008, 29(1): 18–23. |
| [14] |
孙晓彤, 童力, 郑为民, 等. 基于多重网格的射电源条纹搜索算法研究[J]. 天文研究与技术, 2021, 18(1): 52–59 SUN X T, TONG L, ZHENG W M, et al. Research on radio source fringe search algorithm based on multi-grid[J]. Astronomical Research & Technology, 2021, 18(1): 52–59. |
| [15] | 郭丽. 基于VLBI跟踪观测的空间飞行器瞬时状态参量归算[D]. 上海: 中国科学院上海天文台, 2007. GUO L. Reduction of the instantaneous state vectors of spacecraft based on VLBI tracking data[D]. Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences, 2007. |



