脉冲星是快速旋转的中子星,因不断发出电磁脉冲信号而得名。脉冲星是20世纪60年代天文学的重要发现之一[1]。对脉冲星的研究可以为拥有极端物理属性的中子星研究提供重要信息,极大地推动物理、天文、导航和时间度量等领域的发展[2-3]。基于脉冲星信号的周期性特征,利用快速傅里叶变换将时间域信号转换为频率域信号,并结合快速折叠算法成为探测脉冲星信号的主要方法[4]。随着对脉冲信号的挖掘,近年来相继发现了两类没有周期性特征的天文脉冲信号,它们分别来自旋转瞬间射电体(Rotating Radio Transients, RRATs)和快速射电暴(Fast Radio Bursts, FRBs)[2, 5-6]。旋转瞬间射电体信号的发射在时间上非常零星和分散,无法在传统的周期性搜寻中发现它们。快速射电暴由银河系外的射电突发信号组成,目前发现极个别的周期性现象,但仍然以缺乏周期性为主要特征。这两类天文现象的脉冲信号,由于它们转瞬即逝的特征,称之为单脉冲天体信号。单脉冲信号的搜寻不但是周期性信号搜寻方法的有益补充,而且是旋转瞬间射电体和快速射电暴的主要探测方法[4]。
目前,单脉冲信号的识别方法主要分为启发式阈值搜寻算法和机器学习算法。启发式搜寻是一种利用问题所具有的启发信息来引导搜寻、发现目标的算法,该算法通过减小搜寻范围降低问题的复杂性,提高计算效率。这类方法主要是基于文[2]提出的单脉冲信号分类框架,该框架将单脉冲信号的提取分为消色散、匹配滤波、阈值化和判断等4个步骤,以判断被检测信号中单脉冲信号是否存在。例如,文[7]使用一种聚类算法将信噪比高于一定阈值的疑似脉冲事件筛选为单脉冲候选体。文[8]根据色散和信号时间对脉冲事件进行分组,然后基于相邻分组中最大信噪比判断脉冲信号是否有峰值,据此筛选并创建诊断图以供人工检查。文[9]进一步提出了一种简单的递归峰值识别算法,利用弥散脉冲组(Dispersed Pulse Groups, DPG)拟合线的斜率来识别大斜率趋势,并据此筛选单脉冲事件候选体。这些方法虽然在检测脉冲信号时有一定的作用,但是它们主要依靠阈值分割提取脉冲星信号,所采用的特征来源于分组中最强的脉冲信号,由此导致它们精度有限,且需要大量人工参与,难以适应大规模、海量的数据处理。
近年来,随着传感器技术的发展和大规模射电巡天的推进,机器学习已经成为脉冲星信号识别的重要途经[10]。机器学习方法是通过对已知脉冲星信号的特征进行统计分析,建立学习模型,然后利用学习模型对未知脉冲信号进行判断的方法。该方法通常有4个步骤:(1)建立基准数据集;(2)特征提取;(3)模型训练与评价;(4)模型应用。文[11]在总结利用机器学习筛选脉冲信号时指出,目前已有的机器学习算法主要用于周期性脉冲信号的搜寻。例如,人工神经网络(Artificial Neural Network, ANN)算法[12-14]和模式识别算法[15]都在周期性脉冲信号搜寻中得到应用。虽然机器学习在周期性脉冲信号中已经有了许多探索,但在单脉冲信号识别中的应用才刚刚开始,并逐渐受到重视。单脉冲信号识别的机器学习应用方面,文[12]在启发式阈值搜寻算法的基础上,挑选了信噪比、脉冲宽度等12个特征作为三层人工神经网络的输入,首次以机器学习的方法进行单脉冲信号筛选。文[9]利用绿岸射电望远镜(Green Bank Telescope, GBT)观测的数据集,从脉冲数量-色散图、信噪比-色散图中提取16个特征,比较了支持向量机(Support Vector Machines, SVM)、人工神经网络、规则归纳法(Rule Induction, RULE)和决策树等方法,实验结果表明,使用随机森林集成树的分类器在查全率和查准率方面有最佳的整体效果。文[16]以低频射电联合阵列巡天(LOFAR Tied-Array All-sky Survey, LOTAAS)数据集为例,根据每个特征的信息增益,筛选用于单脉冲信号分类的5个重要指标:峰值检测窗口宽度、脉冲色散平均值、脉冲信噪比、窗口宽度分布曲线超额峰度和信噪比分布曲线超额峰度,通过比较几种不同的机器学习算法,认为基于高斯-海灵格快速决策树的方法在单脉冲信号分类中具有最好的性能。
从以往的研究来看,基于决策树的方法是性能最好的方法之一,但是对决策树模型的参数估计大多采用小规模随机抽样的方法计算,无法保证分类结果最优。近些年机器学习领域对决策树模型进行了改进和提升,尤其是基于梯度提升的GBDT和XGBoost算法在许多领域都得到了广泛的应用[17]。因此,本文旨在探讨XGBoost结合包裹式特征选择方法进行单脉冲信号识别的性能分析。
1 数据 1.1 数据来源良好的基准数据集是进行机器学习训练应用和研究的基础,然而面对海量的脉冲信号,对脉冲信号进行标注是短期难以完成的事情。因此在本文中,我们直接使用文[15]已标注的数据集用于模型的研究,此数据集来源于低频射电联合阵列巡天项目。低频射电阵列由荷兰射电天文研究所主持研发,是一种由数千个天线组成的大型射电望远镜阵列,这些天线分组分布在荷兰和其他欧洲国家的观测站点,在最低频段以高分辨率和高灵敏度进行脉冲星广泛且深入的研究[18]。低频射电联合阵列巡天项目利用其中12个子站进行观测,对天空的每个指向产生222个同时段的射电数据,每次观测时间持续1 h,记录数据的时间分辨率为0.492 ms,每小时可以接收16.9 TB的原始数据[19]。本文实验所用数据集是从历次观测中抽取的。
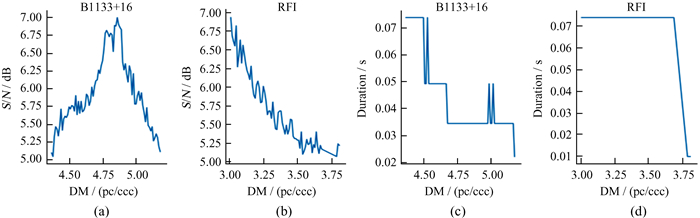
1.2 数据预处理过程脉冲星的搜寻大致需要4个阶段,分别是射电信号数据收集、消色散处理、周期性脉冲或单脉冲搜寻以及人工判别[3]。色散效应是天体物理信号和射频干扰信号的重要区别之一[20]。天体物理信号到达地球时受空间不同密度自由电子的影响,不同频率的信号产生不同的延迟效应。色散是对信号传播方向上自由电子总数量的度量。由于事先不知道天体信号对应的色散,所以在消色散处理时,需要用不同的色散值尝试。由此可知,对于一个单脉冲信号,虽然本质上对应着唯一一个色散,但经过消色散处理会生成很多根据不同消色散得到的候选脉冲信号,这些不同的候选脉冲信号仍然可能被检测为峰值信号。这样,理论上一个脉冲信号可能被检测为多个峰值信号,它们对应的色散值非常接近。因此,我们可以通过对被检测的一系列峰值信号按照对应的色散值进行聚类分析,聚集到一起的峰值信号形成一个弥散脉冲组。图 1(a)展示了一个弥散脉冲组中不同色散值时的脉冲信号的信噪比分布。对单脉冲信号的识别,主要识别弥散脉冲组是来源于脉冲星还是射频干扰,如果被识别为脉冲星信号,则输出特征图信息,供人工进一步判断。
|
| 图 1 单脉冲和射频干扰弥散脉冲组事件分布示意图 Fig. 1 DPG distribution curve of S/N and Duration for single pulse and RFI |
本文所采用的数据是在0~550 pc cm-3的色散范围内,对色散每隔0.01~0.1 pc cm-3进行一次计算处理得到的。对色散处理后的数据,采用不同长度的矩形窗进行峰值检测,将信噪比大于5的信号保存,形成一个信号事件表,保存的信息包括窗口宽度、色散、信号时间等。基于信号事件表中每条记录的信号时间和色散值的邻近程度,对信号事件进行聚类分组,对信号时间在30 ms内、色散差值在2 pc cm-3内的信号事件归为一个弥散脉冲组。图 1展示了脉冲星编号为B1133+16的一个弥散脉冲组的信号事件分布情况,以及一个射频干扰信号构成的弥散脉冲组的分布情况。从图 1可以看出,脉冲星信号和射频干扰信号的弥散脉冲组在信噪比分布曲线形态上有显著差异,窗口宽度的分布曲线也有明显差异,这些形态特征有助于脉冲星弥散脉冲组的识别。
1.3 数据特征设计经过滤波和峰值检测筛选后,信号事件表记录的总数约374万条,形成弥散脉冲组53 066条,其中35 063条为射频干扰,18 003条为47个已知脉冲星。对弥散脉冲组的特征设计是进行正确分类的重要内容,参考已有弥散脉冲组特征应用的方法,本文设计以下特征:
(1) 色散(Dispersion Measure, DM),是脉冲星和地球之间沿信号传播方向的自由电子积分柱密度,单位pc cm-3,一个弥散脉冲组的色散值取其中最强的信号事件对应的色散值。
(2) 信噪比(S/N),是信号和噪声的比值,即射电望远镜接收信号的电压与同时记录的噪声电压的比值。信噪比越高,信号越强,噪声越弱。信噪比是判断脉冲事件的主要依据,一个弥散脉冲组的信噪比取其中最强信号事件对应的信噪比。
(3) 窗口宽度(Duration),对时间序列信号进行峰值检测时,所用的矩形窗函数的窗口宽度,即窗口的时间范围,是用于峰值提取的计算参数。峰值检测采用一系列不同的窗口宽度,不同的窗口宽度可能检出不同的峰值结果。一个弥散脉冲组的窗口宽度取其中最强的信号事件对应的窗口宽度。
(4) 色散范围(DM Extent, DM_E),是一个弥散脉冲组中所有信号事件对应的色散值范围,即图 1第1个子图中曲线的覆盖范围。
(5) 时间范围(Time Extent, Time_E),是一个弥散脉冲组中所有信号事件对应的时间范围,单位s。
(6) 事件个数(Number of Events, N_Events),是一个弥散脉冲组包含的信号事件的数量,事件数量太少说明没有太强的色散效应,大概率不是脉冲星信号。
(7) 色散平均值(Average DM, aDM),是同一个弥散脉冲组的所有信号事件的平均色散。
(8) 脉冲平均时间(Average Time of Pulse, aTime),形成一个弥散脉冲组的所有信号的平均时间。因为低频射电联合阵列巡天项目利用12个子站同时观测,对天空的每个指向产生222个天体辐射数据,这些数据经过预处理,形成很多不同时间序列的数据,脉冲平均时间对于判断不同时间序列的脉冲信号是否来自同一天体有一定帮助。对于脉冲星信号,多个子站可能同时观测到,而对于射频干扰信号,往往只有一个子站观测到。
(9) 信噪比分布曲线超额峰度(KurtSigma):形成一个弥散脉冲组所有信号的信噪比分布曲线的峰度减去正态分布的峰度,即图 1(a)和(b)中曲线的峰度减去正态分布的峰度,正态分布的峰度系数为3。
(10) 窗口宽度分布曲线超额峰度(KurtDuration):形成一个弥散脉冲组的每个事件在峰值检测时所用窗口宽度的分布曲线峰度减去正态分布的峰度,即图 1(c)和(d)分布曲线的峰度减去正态分布的峰度。
2 方法 2.1 包裹式特征选择特征选择的目的在于去除与当前学习任务无关和冗余的特征,降低学习任务的难度,促进对特征和问题的理解,关键是建立一种评价标准区分哪些特征组合有助于识别。为了增强特征与模型之间的相关性,提升模型性能,识别前,本文采用包裹法进行特征选择。
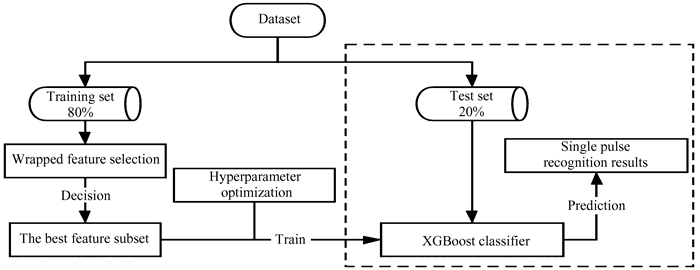
包裹式特征选择方法与后续任务选用的分类学习器直接相关,以学习器的性能作为特征子集的评估准则,即包裹式特征选择方法直接针对给定学习器进行优化(图 2)。因此,包裹式特征选择方法决策的特征子集最易与当前选用的分类器契合。

|
| 图 2 包裹式特征选择 Fig. 2 Wrapped method for feature selection |
本文采用递归特征消除(Recursive feature elimination, RFE)的方法实现包裹式特征选择。分类器在给定的特征集合上进行训练,再从当前的特征集合中移除最不重要的特征,在新的特征集合上继续训练。不断重复递归过程,直到最终达到所需要的特征数量,选出最优的特征子集。对于给定分类器,最后选出的特征子集包含的特征就是最重要的特征。
2.2 XGBoost分类学习器XGBoost是一种集成学习算法,在决策树的基础上采用集成策略。XGBoost包含一个迭代残差树的集合,利用梯度提升算法,不断减小已生成的决策树的损失,每一棵树都在学习前面所有树的残差,将每棵树预测的结果相加作为样本的最终预测结果。
XGBoost利用向前分布算法,学习到包含K棵树的加法模型为
| $ \hat{y}_{i}=\sum\limits_{t=1}^{K} f_{t}\left(x_{i}\right) \quad f_{t} \in F , $ | (1) |
其中,K为树的总数;ft为第t棵树;xi为输入样本;
为了求解整个决策树的函数空间,需要不断优化目标函数,XGBoost的整体目标函数可以表示为[21]
| $ {Obj}^{(t)}=\sum\limits_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}\right)+\sum\limits_{k=1}^{t} \varOmega\left(f_{k}\right), $ | (2) |
其中,
首先,通过贪心算法寻找局部最优解:
| $ \hat{y}_{i}^{(t)}=\sum\limits_{j=1}^{t} f_{j}\left(x_{i}\right)=\hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right), $ | (3) |
其中,
| $ O b j^{(t)}=\sum\limits_{i=1}^{n} l\left[y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right]+\varOmega\left(f_{t}\right)+C . $ | (4) |
其次,对目标函数采用二阶泰勒近似展开得到
| $ O b j^{(t)}=\sum\limits_{i=1}^{n}\left[l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\varOmega\left(f_{t}\right)+C , $ | (5) |
其中,gi和hi分别为误差函数的一阶导数和二阶导数:
| $ \begin{aligned} &g_{i}=\partial_{\hat{y}(t-1)} l\left(y_{i}, \quad \hat{y}_{i}^{(t-1)}\right), \\ &h_{i}=\partial_{\hat{y}(t-1)}^{2} l\left(y_{i}, \quad \hat{y}_{i}^{(t-1)}\right). \end{aligned} $ |
移除对第t轮迭代来说为常数项的
| $ O b j^{(t)}=\sum\limits_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\varOmega\left(f_{t}\right) . $ | (6) |
XGboost中正则项用来衡量树的复杂度,
| $ \varOmega\left(f_{t}\right)=\gamma T+\frac{1}{2} \lambda \sum\limits_{j=1}^{T} \omega_{j}^{2}, $ | (7) |
其中,T为每棵树的节点数量;ω为每棵树的叶子节点的输出分数;γ和λ为常数。进一步将目标函数表示为
| $ O b j^{(t)}=\sum\limits_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\gamma T+\frac{1}{2} \lambda \sum\limits_{j=1}^{T} \omega_{j}^{2}. $ | (8) |
将输入的xi映射到叶子节点,则有ft(xi)=ωq(xi), ω∈RT, q: Rd→{1, 2, …, T},并定义每个叶子节点j的样本集合为Ij={iq(xi)=j}。此时,目标函数可以表示为
| $ O b j^{(t)}=\sum\limits_{j=1}^{T}\left[G_{j} \omega_{j}+\frac{1}{2}\left(H_{j}+\lambda\right) \omega_{j}^{2}\right]+\gamma T, $ | (9) |
其中,
最后,对目标函数进行优化,计算第t轮时使目标函数最小的叶子节点的输出分数ω,直接对ω求导,使导数为0,得到
| $ \omega_{j}=-\frac{G_{j}}{H_{j}+\lambda} . $ | (10) |
将(10)式代入(9)式,得到最终优化的目标函数
| $ O b j^{(t)}=-\frac{1}{2} \sum\limits_{j=1}^{T}\left(\frac{G_{j}^{2}}{H_{j}+\lambda}\right)+\gamma T . $ | (11) |
在选择特征属性进行节点分裂时,XGBoost会利用贪心算法或近似贪心算法遍历所有特征的划分点,分别计算对应的目标函数值的增益,选择最优的特征进行分裂。当新的分裂带来的增益小于设定的阈值或达到设定的最大深度时,停止树的生长。XGBoost对代价函数进行二阶泰勒展开,还引入缩减、行抽样和列抽样等操作,具有良好的预防过拟合、较高的计算效率和泛化能力的特性。对于XGBoost的程序实现可以直接采用基于Python语言的机器学习工具包Scikit-learn。
2.3 特征筛选评价流程基于上述理论和方法,本文将包裹式特征选择和XGBoost算法相结合,根据输入的数据集,设定一个阈值,取在该阈值下的最佳特征子集,并将得到的特征子集输入XGBoost算法用于分类,得到结果。具体流程如图 3。
|
| 图 3 XGBoost结合包裹式特征选择算法流程图 Fig. 3 Model flowchart of feture selection with XGBoost |
为了分析当前算法的分类效果,我们利用混淆矩阵对模型的预测结果进行评价。本文数据集分为射频干扰弥散脉冲组和单脉冲弥散脉冲组。如果一个脉冲星的弥散脉冲组被正确识别为单脉冲信号,称为真阳性(True Positive, TP),若被错误地识别为射频干扰信号,称为伪阴性(False Negative, FN)。同样,如果一个射频干扰被错误地识别为单脉冲信号,称为假阳性(False Positive, FP),若被正确地识别为射频干扰,称为真阴性(True Negative, TN)。表 1为二分类情况下的混淆矩阵。
| Confusion Matrix | Target | ||
| Positive | Negative | ||
| Model | Positive | TP | FP |
| Negative | FN | TN | |
在二分类问题中常用的评价指标有准确率(Accuracy)、误分类率(Error)、精确率(Precision)、召回率(Recall)和F1分数(F1-score)[22]。其中,准确率表示正确分类的样本占总样本的比例,当数据集中存在各类别样本不平衡的情况时,分类器倾向将样本判断为来自比例较大的类别,出现准确率虚高的情况。因此,仅凭准确率不能客观评价算法的性能,还需要引入其他评价指标。精确率表示预测为脉冲星的样本中真正的脉冲星信号所占的比例。召回率表示脉冲星信号被正确识别的比例。精确率和召回率两个指标存在此消彼长的问题,F1分数则综合了精确率和召回率的结果,可以调和平均两个指标,当前算法得到的F1分数越高说明算法的性能整体上越理想。
3 结果与讨论实验使用的数据集包含来自47个已知脉冲星的弥散脉冲组18 003个,射频干扰弥散脉冲组35 063个。具体操作步骤是将数据集随机划分10次,使用交叉验证方法进行模型的训练和评估,其中80%用于训练,剩余的20%用于验证。为了避免在数据分类时出现数据泄露,同时保证单脉冲样本和射频干扰样本尽量均衡,在实验中不是直接对数据集进行随机划分,而是分别将属于47个已知脉冲星的弥散脉冲组和射频干扰弥散脉冲组随机进行10次分组,每次分组将80%,即38个已知脉冲星的弥散脉冲组和射频干扰的弥散脉冲组用于训练,剩余9个用于验证。
为了对比分析,本文除了采用XGBoost方法外,还对GBDT、AdaBoost、随机森林和BP神经网络模型进行了实验对比。为了使结果具有可对比性,对比前每种方法都进行了调优,实验结果选用的都是经调试的最优参数,其中BP神经网络采用三层架构(输入层10个节点,隐藏层56个节点,输出2个节点),学习率为0.001 5,使用交叉熵损失函数和Adam优化器;GBDT和随机森林的最大迭代次数是100,最大深度是20,学习率为2;AdaBoost的最大迭代次数是100。表 2显示了5种模型在该数据集上10次随机划分的平均实验结果。
| Model | Best feature subset | Error rate (Variance) |
Precision (Variance) |
Recall (Variance) |
F1-Score (Variance) |
| XGBoost | Duration, DM, S/N, DM_E, Time_E, N_events, aDM, KurtDuration, KurtSigma | 2.16% (0.000 7) |
97.57% (0.001 2) |
99.28% (0.000 0) |
98.41% (0.000 3) |
| GBDT | Duration, DM, S/N, DM_E, Time_E, aDM, N_events, KurtDuration, KurtSigma | 4.05% (0.000 4) |
96.14% (0.001 0) |
98.12% (0.000 0) |
97.09% (0.000 2) |
| AdaBoost | Duration, DM, S/N, DM_E, Time_E, aDM, aTime, N_events, KurtDuration, KurtSigma | 3.16% (0.000 3) |
96.53% (0.000 7) |
99.02% (0.000 0) |
97.74% (0.000 2) |
| Random forest | Duration, DM, S/N, DM_E, Time_E, aDM, N_events, KurtDuration, KurtSigma | 3.95% (0.001 3) |
95.70% (0.001 6) |
99.18% (0.000 0) |
97.35% (0.000 4) |
| BPNN | Duration, DM, S/N, DM_E, Time_E, aDM, aTime, N_events, KurtDuration, KurtSigma | 3.98% (0.000 1) |
97.47% (0.000 9) |
98.11% (0.000 1) |
97.75% (0.000 2) |
包裹式特征选择的过程紧密结合选用的分类器,通过某种特征搜寻策略在模型上检验多种特征子集的分类性能,表 2列出了不同分类器和其最优特征组合的分类评价结果。从表 2可以看出,5种模型对脉冲星弥散脉冲组和射频干扰弥散脉冲组的分类结果都具有较高的精确率和召回率,特别是XGBoost的精确率、召回率和F1分数是5种模型中最高的,比其他模型平均高出1到2个百分点。从误分类率来看,GBDT的误分类率最高,XGBoost的误分类率最低。综合几个指标的结果可以看出,XGBoost在单脉冲信号弥散脉冲组分类识别方面更有综合优势。
从特征应用上看,色散、信噪比、窗口宽度、色散范围、时间范围、事件个数、色散平均值、窗口宽度分布曲线超额峰度、信噪比分布曲线超额峰度等9个特征参数被5个模型都看作是最优特征组合,AdaBoost和BP神经网络模型进一步把脉冲平均时间也选为最优特征。平均时间没有被其他3个模型选为最优特征,说明该特征对单脉冲识别的作用不是特别显著。
对XGBoost分类器,除了用于模型训练的特征之外,超参数也在一定程度上影响单脉冲识别的结果,其中树的最大深度、模型的学习速率是影响结果性能的主要参数。
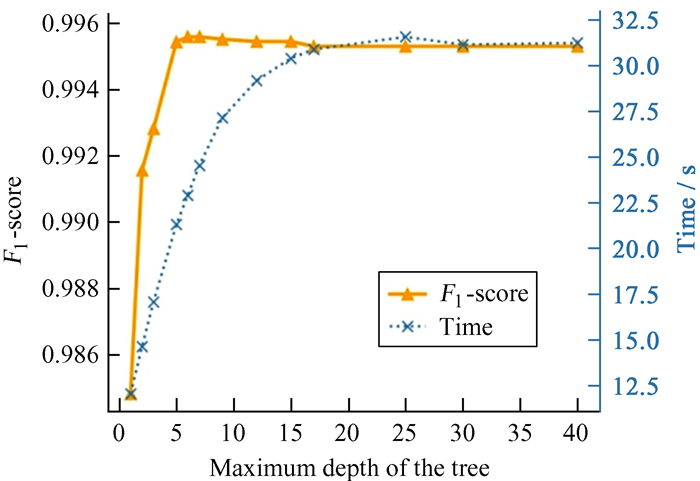
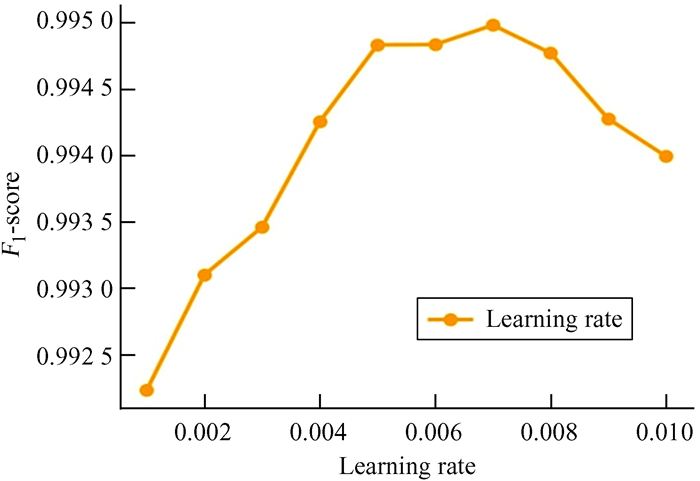
图 4为树的最大深度对模型的训练时间以及F1分数的影响。当树的最大深度小于25时,训练模型消耗的时间稳步上升,而后基本保持平稳不变。模型的F1分数随着树的最大深度变化呈现先升后降而后平稳的趋势。当树的最大深度为6时,XGBoost能够在测试集上获得一个最高的F1分数,且用时相对较短。由此可见,在本文使用的数据集上,树的最大深度为6时能同时权衡训练模型的时间消耗和单脉冲分类任务的性能。图 5展示了学习速率对XGBoost性能的影响。由图 5可知,在学习率达到0.007时,XGBoost能获得最好的分类性能。
|
| 图 4 模型的F1分数与树的最大深度变化关系 Fig. 4 F1-score changes with the maximum depth of the tree |
|
| 图 5 模型的F1分数随学习率的变化趋势 Fig. 5 F1-score changes with model learning rate |
特征数量同样也影响模型对单脉冲识别的性能。在本文所使用的数据集上对10个特征使用XGBoost结合包裹式特征选择算法对特征重要程度进行分析。针对包裹式特征选择算法,我们通过设置不同阈值获得不同规模的最优特征子集,并比较分析基于这些特征子集的模型性能。表 3展示了基于不同规模特征子集训练的XGBoost模型在单脉冲信号识别任务的F1分数。
| Feature count | The best feature subset | F1-score |
| 4 | Duration, DM, S/N, DM_E | 0.970 6 |
| 5 | Duration, DM, S/N, DM_E, aDM | 0.967 8 |
| 6 | Duration, DM, S/N, DM_E, aDM, Time_E | 0.974 1 |
| 7 | Duration, DM, S/N, DM_E, aDM, Time_E, N_events | 0.976 9 |
| 8 | Duration, DM, S/N, DM_E, aDM, Time_E, N_events, KurtSigma | 0.983 8 |
| 9 | Duration, DM, S/N, DM_E, aDM, Time_E, N_events, KurtSigma, KurtDuration | 0.986 6 |
| 10 | Duration, DM, S/N, DM_E, aDM, Time_E, N_events, KurtSigma, KurtDuration, aTime | 0.984 5 |
结果表明,特征的数量也会影响脉冲信号分类的性能。虽然每个特征对模型的影响不同,但输入特征的数量和组合也是影响模型性能的关键因素。可以看出,输入不同数量的特征会得到不同的结果。当特征数量为9,特征为色散、信噪比、窗口宽度、色散范围、时间范围、事件个数、色散平均值、窗口宽度分布曲线超额峰度、信噪比分布曲线超额峰度时,可以获得最高的F1分数。
4 结论近年来,随着周期性脉冲信号探测方法的成熟,单脉冲信号识别成为脉冲星研究的一个重要方向。由于单脉冲信号可以提取的特征相对较少,机器学习成为最主要的方法。设计关键特征,并寻找最优的机器学习算法是当前脉冲星信号识别的关键任务。
本文在前人研究的基础上,将XGBoost分类器与包裹式特征选择相结合,以低频射电联合阵列巡天数据集为例,与AdaBoost、GBDT、随机森林和BP神经网络等模型进行了实验对比。研究结果表明,XGBoost在单脉冲识别方面误分类率更低,精确率、召回率和F1分数更高,是单脉冲信号识别提取的优秀方法。本文在实验设计中,将47个已知脉冲星和射频干扰信号分别随机进行10次分组,有效避免了数据集划分造成数据泄露的影响。如果直接将来自47个脉冲星的18 003个弥散脉冲组进行分组训练和测试,得到精确度将高达99.79%,F1分数高达99.76%。可见训练集和测试集的划分方法对识别结果具有重要影响。
从特征选择上看,本文的实验结果表明,色散、信噪比、窗口宽度、色散范围、时间范围、事件个数、色散平均值、窗口宽度分布曲线超额峰度、信噪比分布曲线超额峰度等9个特征被最多模型选择,具有良好的判别力。
对单脉冲信号进行标注并建立训练数据集是一项费力耗时的工作,需要长期的积累。本文虽然是以低频射电联合阵列巡天数据集作为研究对象,其研究结果和方法可以为我国开展以FAST探测信号为主的单脉冲信号研究与应用提供参考。目前对我国FAST数据的挖掘和应用正在大力推进,并已成功探测到属于单脉冲的快速射电暴[23-24]。另外,随着对单脉冲信号特征的持续分析和挖掘,新的研究方法也将不断提出和改进。
| [1] | HEWISH A. Pulsars as physics laboratories[J]. Interdisciplinary Science Reviews, 1994, 19(1): 70–74. DOI: 10.1179/isr.1994.19.1.70 |
| [2] | CORDES J M, MCLAUGHLIN M A. Searches for fast radio transients[J]. The Astrophysical Journal, 2003, 596(2): 1142–1154. DOI: 10.1086/378231 |
| [3] | DEVINE T R, GOSEVA-POPSTOJANOVA K, MCLAUGHLIN M. Detection of dispersed radio pulses: a machine learning approach to candidate identification and classification[J]. Monthly Notices of the Royal Astronomical Society, 2016, 459(2): 1519–1532. DOI: 10.1093/mnras/stw655 |
| [4] | PATEL C, AGARWAL D, BHARDWAJ M, et al. PALFA single-pulse pipeline: new pulsars, rotating radio transients, and a candidate fast radio burst[J]. The Astrophysical Journal, 2018, 869(2): 181. DOI: 10.3847/1538-4357/aaee65 |
| [5] | MCLAUGHLIN M, LYNE A, LORIMER D, et al. Transient radio bursts from rotating neutron stars[J]. Nature, 2006, 439(7078): 817–820. DOI: 10.1038/nature04440 |
| [6] | LORIMER D R, BAILES M, MCLAUGHLIN M A, et al. A bright millisecond radio burst of extragalactic origin[J]. Science, 2007, 318(5851): 777–780. DOI: 10.1126/science.1147532 |
| [7] | DENEVA J S, CORDES J M, MCLAUGHLIN M A, et al. Arecibo pulsar survey using ALFA: probing radio pulsar intermittency and transients[J]. The Astrophysical Journal, 2009, 703(2): 2259–2274. DOI: 10.1088/0004-637X/703/2/2259 |
| [8] | KARAKO-ARGAMAN C, KASPI V M, LYNCH R S, et al. Discovery and follow-up of rotating radio transients with the Green Bank and LOFAR telescopes[J]. The Astrophysical Journal, 2015, 809(1): 67. DOI: 10.1088/0004-637X/809/1/67 |
| [9] | DEVINE T R, GOSEVA-POPSTOJANOVA K, MCLAUGHLIN M. Detection of dispersed radio pulses: a machine learning approach to candidate identification and classification[J]. Monthly Notices of the Royal Astronomical Society, 2016, 459(2): 1519–1532. DOI: 10.1093/mnras/stw655 |
| [10] |
王元超, 郑建华, 潘之辰, 等. 脉冲星候选样本分类方法综述[J]. 深空探测学报, 2018, 5(3): 203–211 WANG Y C, ZHENG J H, PAN Z C, et al. An overview of pulsar candidate classification methods[J]. Journal of Deep Space Exploration, 2018, 5(3): 203–211. |
| [11] | MCFADDEN R, KARASTERGIOU A, ROBERTS S. Machine learning for pulsar detection[C]// Proceedings of the International Astronomical Union. 2017: 372-373. |
| [12] | EATOUGH R P, MOLKENTHIN N, KRAMER M, et al. Selection of radio pulsar candidates using artificial neural networks[J]. Monthly Notices of the Royal Astronomical Society, 2010, 407(4): 2443–2450. DOI: 10.1111/j.1365-2966.2010.17082.x |
| [13] | BATES S D, BAILES M, BARSDELL B R, et al. The high time resolution universe pulsar survey-Ⅵ. An artificial neural network and timing of 75 pulsars[J]. Monthly Notices of the Royal Astronomical Societ, 2012, 427(2): 1052–1065. DOI: 10.1111/j.1365-2966.2012.22042.x |
| [14] | MORELLO V, BARR E D, BAILES M, et al. SPINN: a straightforward machine learning solution to the pulsar candidate selection problem[J]. Monthly Notices of the Royal Astronomical Society, 2014, 443(2): 1651–1662. DOI: 10.1093/mnras/stu1188 |
| [15] | ZHU W W, BERNDSEN A, MADSEN E C, et al. Searching for pulsars using image pattern recognition[J]. The Astrophysical Journal, 2014, 781(2): 117. DOI: 10.1088/0004-637X/781/2/117 |
| [16] | MICHILLI D, HESSELS J, LYON R J, et al. Single-pulse classifier for the LOFAR Tied-Array All-Sky Survey[J]. Monthly Notices of the Royal Astronomical Society, 2018, 480(3): 3457–3467. DOI: 10.1093/mnras/sty2072 |
| [17] | CHEN T, GUESTRIN C. XGBoost: a scalable tree boosting system[C]// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2016: 785-794. |
| [18] | COENEN T, VAN LEEUWEN J, HESSELS J W T, et al. The LOFAR pilot surveys for pulsars and fast radio transients[J]. Astronomy & Astrophysics, 2014, 570: A60. |
| [19] | SANIDAS S, COOPER S, BASSA C G, et al. The LOFAR Tied-Array All-Sky Survey (LOTAAS): survey overview and initial pulsar discoveries[J]. Astronomy & Astrophysics, 2019, 626: A104. DOI: 10.1051/0004-6361/201935609 |
| [20] | LORIMER D R, KRAMER M. Handbook of pulsar astronomy[M]. Cambridge: Cambridge University Press, 2012. |
| [21] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012. LI H. Statistical learning method[M]. Beijing: Tsinghua University Press, 2012. |
| [22] | SUTHAHARAN S. Machine learning models and algorithms for big data classification[M]. [S.l.]: Springer, 2016. |
| [23] | ZHU W W, LI D, LUO R, et al. A fast radio burst discovered in FAST drift scan survey[J]. The Astrophysical Journal Letters, 2020, 895: L6. DOI: 10.3847/2041-8213/ab8e46 |
| [24] | NIU C H, LI D, LUO R, et al. CRAFTS for fast radio bursts extending the dispersion-fluence relation with new FRBs detected by FAST[J]. The Astrophysical Journal Letters, 2021, 909: L8. DOI: 10.3847/2041-8213/abe7f0 |



