2. 昆明理工大学云南省计算机应用技术重点实验室,云南 昆明 650500
2. Key Laboratory of Applications of Computer Technology of Yunnan Province, Kunming University of Science and Technology, Kunming 650500, China
大气湍流是大气中一种不规则的随机运动,它使望远镜的实际分辨率远低于衍射极限分辨率,是限制地基光学望远镜空间分辨率的一个主要因素[1]。地面观测要获得接近望远镜衍射极限分辨率的图像,可以使用事后图像恢复或重建技术,而幸运成像是一种用于去除大气湍流影响的事后图像恢复技术[2-3]。幸运成像技术既可以在空域上进行,也可以在频域上进行,但是空域算法的选图主要以帧为单位,这样的选图方式没有考虑图像数据在某些方向的高频分量信息,在数据处理时,导致图像数据信息的浪费。因此,文[4]提出了一种基于傅里叶变换的幸运成像算法,该算法主要由图像预处理、数据选择和数据叠加3部分组成,并对提出的方法进行了模拟实验,实验结果表明,此算法的数据选择率为10%时,成像效果最佳。文[3]以实测数据进一步证实了频域幸运成像的有效性,同时指出该算法相对于空域算法在计算量上存在缺陷。文[5]对传统的频域幸运成像算法进行改进,在频域上采取分组数据选择的方法对传统的频域幸运成像算法进行加速,但该算法仍然属于事后处理的范畴。
上述频域幸运成像算法都是基于中央处理器,因串行的处理方式,难以实时处理,观测人员无法在天文观测过程中准确地了解观测天体的信息,因此,实时化是幸运成像技术发展的必然趋势。近年来,两大并行的硬件加速器引入了图像处理领域[6-7],一个是图形处理器(Graphics Processing Unit, GPU),另一个是现场可编程门阵列。虽然两者都具有强大的并行处理能力,但是现场可编程门阵列是一种半定制型电路,可以根据实际需求编程,而图形处理器一旦设计完成就固定了,因此,图形处理器的灵活度远不如现场可编程门阵列[8]。本文选择现场可编程门阵列实现频域幸运成像算法的加速。
本文根据现场可编程门阵列强大的并行性和灵活性,提出了一个基于现场可编程门阵列的频域幸运成像算法,然后按现场可编程门阵列并行和流水线设计方法,对频域幸运成像算法用Verilog硬件描述语言(Hardware Description Language, HDL)进行设计,并在Xilinx Spartan-7上进行工程实现和相关测试实验。
1 适用于现场可编程门阵列的频域幸运成像算法传统的频域幸运成像算法主要由图像预处理、频域内数据选择和数据叠加3部分组成,在频域内选择数据时,需要消耗大量的时钟资源,导致算法运行速度非常缓慢,属于事后处理的范畴。本节提出一种新的频域幸运成像算法,并在现场可编程门阵列上进行加速,在台式机上验证了算法的有效性。
1.1 算法的总体设计本文提出的基于现场可编程门阵列的频域幸运成像算法既不同于文[3]和文[4]的传统频域幸运成像算法,也不同于文[5]改进的频域幸运成像算法。文[4]提出在频域内以幅值为基准对图像数据进行选择;文[3]证实了频域幸运成像有效性的同时,也指出了该算法计算量大的缺陷;文[5]用分组方法对频域幸运成像算法进行加速,但处理速度仍然非常缓慢。因此,将频域幸运成像技术在现场可编程门阵列上处理是该算法提高处理速度的有效途径。
在现场可编程门阵列上进行频域幸运成像有3个技术难点:
(1) 现场可编程门阵列无法对图像数据直接进行二维快速傅里叶变换。图像数据在现场可编程门阵列上做二维傅里叶变换与在MATLAB平台完全不一样,在MATLAB平台可以直接对图像数据做二维变换,而在现场可编程门阵列上只能做一维傅里叶变换。因此,根据二维傅里叶变换的原理,若有一个N行M列的空域图像数据f(x, y),二维傅里叶变换后的频率点数据为F(u, v),F(u, v)是一个复数,定义为
| $ F(u, v)=\sum\limits_{x=0}^{M-1} \sum\limits_{y=0}^{N-1} f(x, y) \mathrm{e}^{-\mathrm{j} 2 {\text{π}}(u x / M+v y / N)},$ | (1) |
对(1)式进行分解,得到
| $ F(u, v)=\sum\limits_{x=0}^{M-1}\left[\sum\limits_{y=0}^{N-1} f(x, y) \mathrm{e}^{-\mathrm{j} 2 {\text{π}}(v y / N)}\right] \mathrm{e}^{-\mathrm{j} 2 {\text{π}}(u x / M)},$ | (2) |
其中,x,y为空域图像的行数和列数,取值范围为x=0, 1, …, M-1;y=0, 1, …, N-1。u,v为频域图像的行数和列数,取值范围为u=0, 1, …, M-1;v=0, 1, …, N-1。由(1)式和(2)式可知,二维傅里叶变换可以采用将二维转换为两个一维的算法进行处理,即将二维快速傅里叶变换拆分为行方向的快速傅里叶变换和列方向的快速傅里叶变换,然后按先后次序进行计算。通常,一维快速傅里叶变换算法的行列先后顺序对二维快速傅里叶变换运算结果没有影响,由于本系统是对128 × 128的图像进行二维快速傅里叶变换,故N,M都等于128。
(2) 传统的频域幸运成像算法是以幅值为基准选择数据,即按
| $ M(u, v)=\sqrt{\operatorname{Re}[F(u, v)]^{2}+\operatorname{Im}[F(u, v)]^{2}} $ | (3) |
选择数据。其中,Re[F(u, v)]为频域数据的实部;Im[F(u, v)]为频域数据的虚部;M(u, v)为频域数据的模。
虽然现场可编程门阵列可以方便地进行整数的加减乘除运算,但是在现场可编程门阵列上计算复数幅值的算法复杂且耗时,除非调用Cordic知识产权核(International Property, IP),但是此核消耗大量的硬件资源,不适合本系统在中小规模的现场可编程门阵列上实现。因此,本文提出使用频域数据的实部平方与虚部平方之和代替幅值进行数据选择,因为实部平方与虚部平方之和与幅值的变化规律一致,即使用
| $ M^{2}(u, v)=\operatorname{Re}[F(u, v)]^{2}+\operatorname{Im}[F(u, v)]^{2} $ | (4) |
代替(3)式进行数据选择。
(3) 现场可编程门阵列片的存储资源有限。由于本系统需要对大量的图像频域数据进行存储,而片上随机存取存储器(Random Access Memory, RAM)资源远远不足,因此,本系统使用现场可编程门阵列外大容量存储器进行频域图像数据的存储。
本文提出的适用于现场可编程门阵列的频域幸运成像算法工作流程为:
(1) 图像输入,并进行高斯滤波;
(2) 滤波后的图像做行快速傅里叶变换;
(3) 行快速傅里叶变换的结果用乒乓操作的方式在随机存取存储器中进行转置;
(4) 从随机存取存储器中读出数据做列快速傅里叶变换,并将结果存入第3代双倍数据率同步动态随机存取存储器(Double-Data-Rate Three Synchronous Dynamic Random Access Memory, DDR3);
(5) 从DDR3中读出数据,按10%的比例选择数据;
(6) 数据叠加;
(7) 对叠加数据做行快速傅里叶逆变换;
(8) 行傅里叶逆变换的结果在随机存取存储器中进行转置;
(9) 从随机存取存储器中读出数据做列快速傅里叶逆变换;
(10) 将列快速傅里叶逆变换的结果分为两路,一路数据进行二值化,并送入HDMI模块显示,另一路数据传回上位机。
在以上工作流程中,由于现场可编程门阵列具有强大的并行处理能力,第(1)步至第(4)步是并行处理的,第(5)步至第(8)步也是并行处理的。第(1)步图像数据通过精简吉比特介质独立接口(Reduced Gigabit Medium Independent Interface, RGMII)输入,第(2)步至第(4)步是傅里叶正变换过程,即图像数据从空域变换到频域的过程,第(7)步至第(9)步是傅里叶逆变换过程,即图像数据从频域变换到空域的过程。
1.2 算法的验证为了验证该频域幸运成像算法的可行性,同时验证频域幸运成像重建的高分辨率图像比空域幸运成像重建的效果更佳,本文在CPU+MATLAB平台分别做了两组实验,(1)以幅值为基准选择数据的传统频域算法,(2)在MATLAB平台模拟本文提出的算法在现场可编程门阵列上的实现,并与文[9]的实验结果进行对比分析。本实验的硬件平台是Dell Precision T5500图像工作站,内存16 GB,中央处理器为Xeon E5620,显卡为NVIDIA GTX1080,运行的软件环境是Windows 7操作系统和MATLAB R2017a。
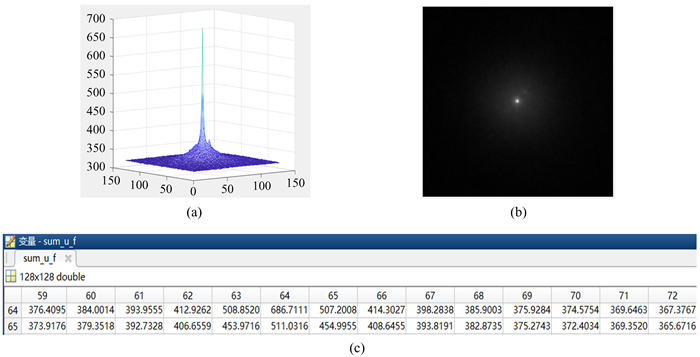
在MATLAB中对随机抽取的2 000帧128 × 128像素的图像进行频域幸运成像算法处理,根据文[4-5]的研究结果,数据选择的比例取10%时,频域幸运成像的效果最好。第1组实验是对文[4]提出的传统频域算法进行复现,其正确性已经过多次验证,本文不再详细介绍;第2组实验是验证本文提出的频域幸运成像算法的正确性。这两组实验的相关结果如图 1和图 2。
|
| 图 1 传统算法的结果。(a)三维灰度分布图;(b)二维灰度图;(c)峰值数据 Fig. 1 The result of traditional algorithm. (a) 3D gray distribution map; (b) 2D gray image; (c) peak data |
|
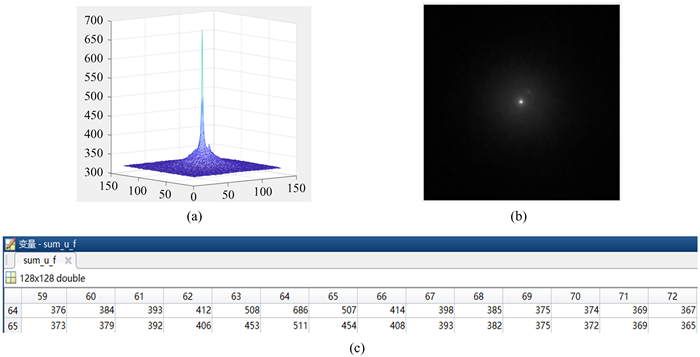
| 图 2 本文提出算法的结果。(a)三维灰度分布图;(b)二维灰度图;(c)峰值数据 Fig. 2 The result of the paper′s algorithm. (a) 3D gray distribution map; (b) 2D gray image; (c) peak data |
根据上述的实验结果,直观上看不出有任何误差,我们对两组实验数据进行分析。如图 1(c)和图 2(c),由于第2组实验是模拟算法在现场可编程门阵列上的实现,所以整个运算过程都是对整数进行处理。从图中数据可以得出,本文提出的适用于现场可编程门阵列的频域算法跟传统的算法仅在小数部分存在误差,即截断误差,这是由于现场可编程门阵列只对整数进行处理造成的。同时,为了进一步分析这两组频域算法重建高分辨率结果图像的优劣,我们选择3种客观的图像质量评价函数,通过数值计算进行对比分析,其中半峰全宽(Full Width at Half Maxima, FWHM)为天文图像常用评价指标,数值越小,说明图像质量越好,其他2种评价函数均为经典的数字图像清晰度评价指标,数值越大,说明图像质量越好。表 1是3种算法分别对2 000帧图像处理得到的高分辨率结果图像的质量评价指标,这3种算法分别是上述两组频域幸运成像算法和文[9]空域幸运成像算法。
从表 1可以看出,本文提出的频域算法与传统的频域算法相比,半峰全宽是一样的,腾格拉德(Tenengrad)梯度和拉普拉斯(Laplacia)梯度值略低于传统的频域算法,这是现场可编程门阵列运算过程中产生截断误差造成的,说明现场可编程门阵列的频域算法得到的高分辨率图像质量比传统算法略差。但是,从表 1中本文提出的频域算法数据和文[9]空域系统的数据对比可知,本文提出的频域算法得到的图像质量(清晰度)远比空域算法得到的图像质量要好,也说明本文提出的频域算法是可行有效的。
既然所提算法是可行有效的,那么只要现场可编程门阵列设计合理,就可以缩短处理时间,加速频域幸运成像,并为实时化提供一种可行的技术方案。所以,在完成上述算法设计后,频域幸运成像系统的现场可编程门阵列实现就成为下一个关键问题。
2 频域幸运成像算法的现场可编程门阵列设计及系统实现算法设计及系统的实现通常与所用硬件平台相关。本文的频域幸运成像算法的硬件平台是以Xilinx公司Spartan-7系列的XC7S50芯片为核心的开发板和一台中央处理器为Xeon E5620的工作站,设计开发环境是Vivado2019.1,采用Vivado平台的内嵌式逻辑分析仪和ModelSim SE 10.7进行硬件设计的验证与调试。在系统的研究过程中,将前面提出的算法用Verilog HDL进行了逻辑设计,并在现场可编程门阵列上实现。本文重点介绍系统的总体设计以及FFT_IFFT模块、数据选择模块的算法及现场可编程门阵列实现。
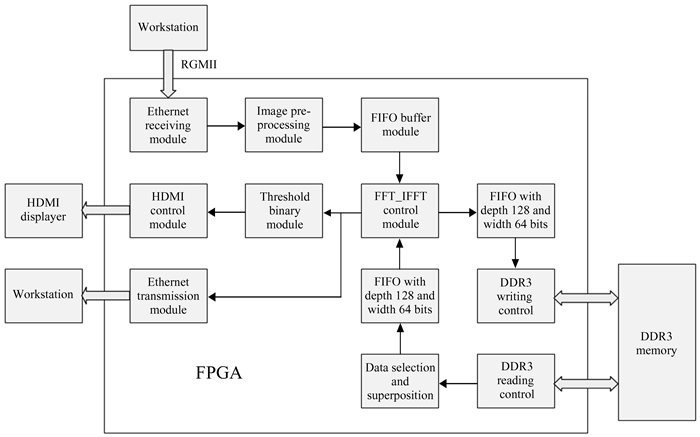
2.1 频域幸运成像系统的总体设计本系统主要包含3部分,即数据传输、数据运算和数据存储。由于系统将来要面向实时应用,对数据的传输速度要求比较高,因此,系统采用千兆以太网进行数据传输。在数据的运算方面,主要涉及二维快速傅里叶变换,而现场可编程门阵列无法对图像数据直接做二维快速傅里叶变换,故本文使用将二维转换为两个一维的方式对天文图像数据做二维快速傅里叶变换。在数据的存储方面,系统使用第3代双倍数据率同步动态随机存取存储器,因为本文是对2 000帧128 × 128像素的图像进行处理,而现场可编程门阵列的片上随机存取存储器资源无法满足本系统的存储要求,故采用片外第3代双倍数据率同步动态随机存取存储器对数据进行储存,并用Verilog HDL实现系统设计。系统的总体结构框图如图 3。
|
| 图 3 系统的总体结构框图 Fig. 3 Overall structure of the system |
由于受到系统使用的现场可编程门阵列硬件平台片上随机存取存储器资源的限制,目前只能使用2 000帧128 × 128像素的短曝光图像作为原始图像进行频域幸运成像处理,并最终以128 × 128像素显示频域幸运成像的结果。
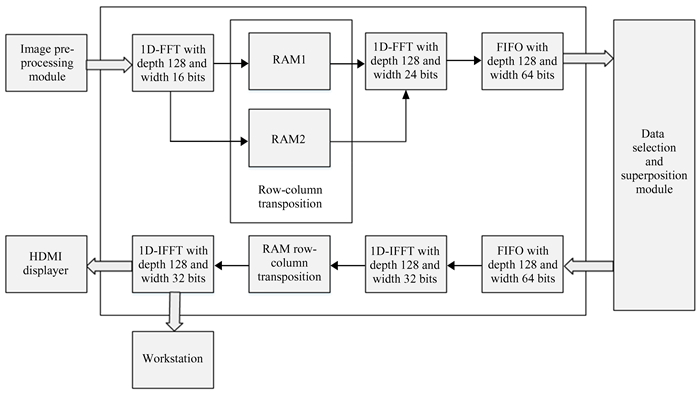
2.2 FFT_IFFT算法及实现模块设计传统的空域幸运成像算法是在空域进行选图和叠加,而频域幸运成像算法则是在傅里叶图像的每个频率点进行数据选择和叠加,因此,要想实现频域幸运成像,必须将图像数据做傅里叶变换,并在频域进行数据的选择和叠加。Xilinx公司在Vivado平台提供了一维快速傅里叶变换的IP核,但由于图像数据是二维的,因此并不能直接使用一维快速傅里叶变换对空域图像数据进行运算,因此,本模块使用将二维转换为两个一维的方式对空域图像做二维傅里叶变换。系统的FFT_IFFT模块设计结构框图如图 4。
|
| 图 4 2D-FFT模块的结构框图 Fig. 4 The structure of 2D-FFT module |
FFT_IFFT模块的工作流程为(1)将预处理模块处理后的数据先进行快速傅里叶行变换,再将行变换的结果在RAM1和RAM2中转置。这里使用两个深度16 384、宽度48位的简单双端口随机存取存储器进行乒乓操作(本系统原始图像数据为16位,经一次傅里叶正变换后,得到的实部和虚部数据各24位,故这里使用宽度48位的随机存取存储器进行转置操作),即当RAM1写满1帧图像数据时进行读操作,读出的数据做快速傅里叶列变换,此时RAM2进行写操作;当RAM2写满1帧图像数据时进行读操作,读出的数据做快速傅里叶列变换,此时RAM1进行写操作。最后将行列变换后的频域数据存入第3代双倍数据率同步动态随机存取存储器进行数据选择和叠加。(2)将选择叠加后的数据先进行行IFFT,再将逆变换的结果存入随机存取存储器。这里使用一个深度16 384、宽度64位的简单双端口随机存取存储器进行转置,即当随机存取存储器存完行快速傅里叶逆变换的结果后,再进行列IFFT,即得到叠加后的空域图像数据,并将此数据分为两路,一路数据求平均,然后进行重建高分辨率图像的显示;另一路经以太网发送模块将数据传回上位机。
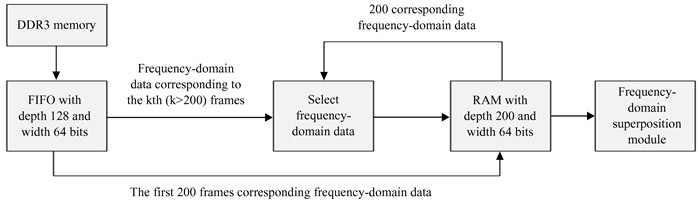
2.3 数据选择算法及实现模块设计传统的数据选择方式是将所有图像对应的频域点的幅值通过排序建立索引关系,选出幅值大小在前10%的频率点数据,这种数据选择的方式计算量非常大,并且消耗的硬件资源也很多,即使是Xilinx推出的高端Vertex-7系列现场可编程门阵列也无法满足这种数据选择方式所消耗的硬件资源。因此,第一,本文使用选择数据但不排序的方式进行数据选择,第二,本文使用频域数据的实部平方与虚部平方之和代替幅值选择数据,具体的模块设计结构框图如图 5。
|
| 图 5 数据选择模块的结构框图 Fig. 5 The structure of data selection module |
数据选择的工作流程。首先,从第3代双倍数据率同步动态随机存取存储器中读出图像的频域数据,读完第1帧图像的第1个数据经FIFO(First In First Out)存入随机存取存储器,读出第2帧图像相对应的数据(即第1个数据),且以同样的方式存入随机存取存储器,一直到第200帧相对应的数据存入随机存取存储器,即从第201帧开始,读出相对应的数据先存入FIFO,并在该数据存入随机存取存储器之前,将随机存取存储器中前200相对应点数据的实部平方与虚部平方之和进行比较,找出最小的数值及地址,再将该任意数据的实部平方与虚部平方之和跟前面找出的最小数值进行比较,若大于前面找出的最小值,则将该数据存入前面找出最小值的地址,否则直接舍去。从第202帧到第2 000帧,一直重复第201帧的第1个数据的过程,当第2 000帧相对应的数据存完后,随机存取存储器将这200个数据送到叠加模块进行叠加。其次,将每帧图像的第2个至第16 384个数据重复前述操作,即完成所有图像的频域数据选择。
3 实验结果及对比分析为了验证本文提出的数据选择方法在现场可编程门阵列上的实现是正确的,我们使用内嵌式逻辑分析仪对数据选择模块的数据进行抓取。为了验证频域幸运成像算法在现场可编程门阵列上实现的正确性,本文以同样的算法在CPU+MATLAB平台进行模拟实验,并将此算法在两个平台的处理结果进行对比分析。
本文采用2016年10月20日云南天文台丽江观测站对天文双星HDS 70的观测图像,共10 000帧,这组图像的观测条件和参数见文[10]。对于图像帧数以及图像大小的选取,因受现场可编程门阵列硬件资源的限制,我们多次随机从10 000帧图像中抽取2 000帧,并裁剪成128 × 128像素的天文目标短曝光图像。
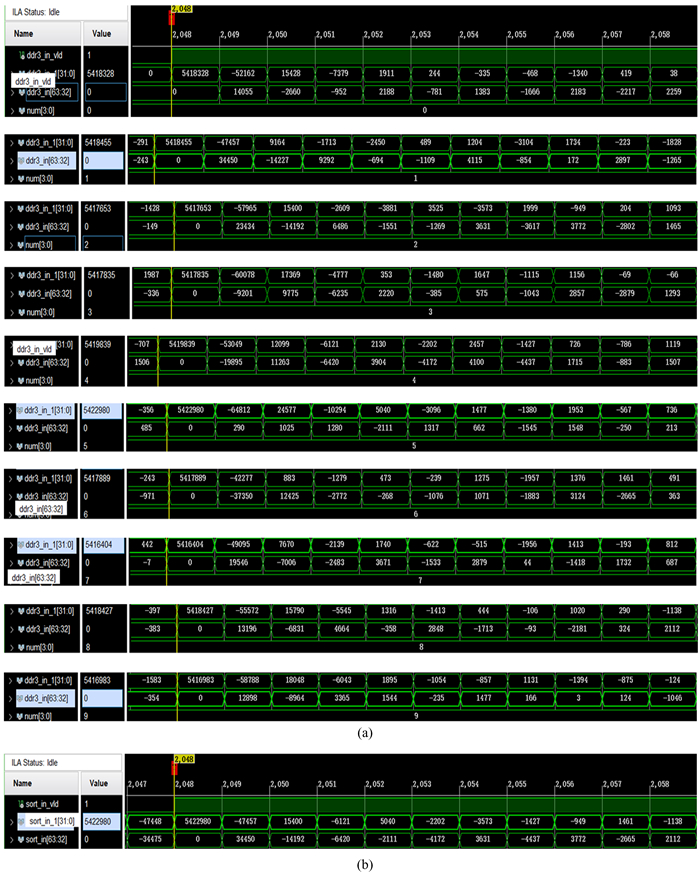
3.1 频域幸运成像在现场可编程门阵列上的实验结果及对比分析 3.1.1 数据选择算法结果本系统采用2 000帧图像每个相对应的频率点选出200个频率点的数据选择方法,即10%的数据选择比例。为了内嵌逻辑分析仪抓取的数据更加直观,这里截取前10行的部分数据按10%的比例进行数据选择,即10行数据选出1行。数据选择结果如图 6。
|
| 图 6 数据选择的结果。(a)前10行的部分数据;(b)选出的数据 Fig. 6 The result of the data selection. (a) The part data of the first 10 lines; (b) selected data |
从图 6(a)和图 6(b)可以看出,每行相对应数据的实部平方与虚部平方之和最大的那个数被选出,同样也是幅值最大的那个数被选出,说明内嵌逻辑分析仪抓取的数据结果正确,本文提出的数据选择算法正确。
3.1.2 频域幸运成像在现场可编程门阵列和MATLAB上的结果分析本系统的硬件平台是以Xilinx公司Spartan-7系列的XC7S50芯片为核心的开发板。系统基于现场可编程门阵列实现的频域幸运成像算法的验证,采用10%的数据选择比例。由于在MATLAB和现场可编程门阵列所得的高分辨率图像不易进行比较,故本系统在现场可编程门阵列和MATLAB上均对算法处理所得的高分辨率图像做相同的锐化,突出高分辨率图像中感兴趣的目标或区域,分别得到了如图 7(a)和图 7(b)的锐化图像。

|
| 图 7 频域幸运成像处理结果。(a)现场可编程门阵列处理结果;(b)MATLAB处理结果 Fig. 7 Result of frequency-domain lucky imaging. (a) Result of FPGA processing; (b) result of MATLAB processing |
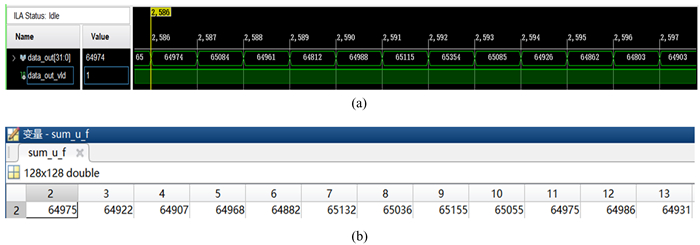
图 7(a)是由以太网回传到上位机的图像数据经锐化后调用MATLAB函数显示的结果,图 7(b)是在MATLAB上进行频域幸运成像算法处理并做相同锐化后的结果。通过对比可以看出,两帧图像完全相同,从而验证了系统在现场可编程门阵列上实现的频域幸运成像算法正确。但是,由于现场可编程门阵列只能处理整数,所以在进行快速傅里叶变换时,产生截断误差,不过该误差非常小,通常在一个数以内。为了使数据的对比更加直观,在重建后的高分辨率图像数据做平均之前(即200帧图像叠加后的结果),我们随机截取一段现场可编程门阵列处理后的数据(使用内嵌式逻辑分析仪抓取数据)与MATLAB处理后的数据进行对比,发现大部分数据误差在200以内,即做完平均后误差基本在1以内,说明图像数据在做快速傅里叶变换时产生的截断误差对图像质量的影响很小。随机截取的数据如图 8(a)和8(b)。
|
| 图 8 频域幸运成像处理结果的部分数据。(a)现场可编程门阵列处理结果;(b)MATLAB处理结果 Fig. 8 The part data of frequency-domain lucky imaging results. (a) Result of FPGA processing; (b) result of MATLAB processing |
将本文基于现场可编程门阵列频域幸运成像算法和文[9]提出的基于现场可编程门阵列幸运成像算法(空域)对1 000帧原始图像进行成像实验,对比算法运行时间、图像数据读取时间和总运行时间,结果如表 2。
由于频域幸运成像算法处理的数据量远比空域幸运成像要多,因此,频域幸运成像的算法复杂度也比空域幸运成像要高得多,但是从表 2可以看出,本文的频域幸运成像算法在现场可编程门阵列上的处理速度比文[9]的空域系统快0.51 s,说明本算法充分利用了现场可编程门阵列的并行性和灵活性优势。本系统像素读取速度比文[9]的空域系统快8.4倍,这是因为本系统采用千兆以太网传输方式取代SD卡的传输方式。本系统的平均运行速度是文[9]空域系统的6.4倍,说明本算法在现场可编程门阵列实现的合理性与正确性。
4 结论本文在分析文[4]基于傅里叶变换的幸运成像算法以及文[5]改进的频域幸运成像算法后,提出了基于现场可编程门阵列的频域幸运成像算法,并将算法在现场可编程门阵列上实现了加速。首先,本文对算法进行了详细的概述,并在MATLAB上验证了该算法是可行有效的,同时验证了本文的频域算法在成像效果上优于空域算法;其次,本文对算法的总体设计以及二维快速傅里叶变换模块、数据选择模块和数据叠加模块的设计思路进行了介绍;最后,本文在一块中小规模、低成本的现场可编程门阵列开发板上进行了系统实现,并展示了相应模块的测试结果与验证过程。由于MATLAB的代码效率比较低,不太适合用于天文观测,而比较合适做算法验证或实验结果分析,因此,本文将该频域系统在现场可编程门阵列上的实验结果与MATLAB平台的实验结果进行了对比,证明了系统在现场可编程门阵列上实现的正确性。虽然本文设计方案还存在不足之处,跟动态实时化相比还有一定的差距,但是就频域幸运成像算法在现场可编程门阵列上的具体实现,并在现场可编程门阵列上实现了加速处理,为频域幸运成像的实时化提供了一种可行的技术方案。
致谢: 本文实验所用双星HDS 70的短曝光图像原始数据由中国科学院云南天文台张西亮提供,特此致谢。
| [1] | OSCOZ A, REBOLO R, LOPEZ R, et al. FastCam: a new lucky imaging instrument for medium-sized telescopes[C]// Proceeding of SPIE. 2008. |
| [2] | BALDWIN J E, MACKAY C D, LAW N M. Lucky imaging: high angular resolution imaging in the visible from the ground[J]. Astronomy & Astrophysics, 2006, 446(2): 739–745. |
| [3] | MACKAY C D. High-efficiency lucky imaging[J]. Monthly Notices of the Royal Astronomical Society, 2013, 432(1): 702–710. DOI: 10.1093/mnras/stt507 |
| [4] | GARREL V, GUYON O, BAUDOZ P. A highly efficient lucky imaging algorithm: image synthesis based on fourier amplitude selection[J]. Publications of the Astronomical Society of the Pacific, 2012, 124(918): 861–867. DOI: 10.1086/667399 |
| [5] | 胡兴. 频域幸运成像算法研究[D]. 昆明: 昆明理工大学, 2019. HU X. Research on frequency-domain lucky imaging algorithm[D]. Kunming: Kunming University of Science and Technology, 2019. |
| [6] |
郭诚欣, 陈红, 孙辉, 等. 基于现代硬件的并行内存排序方法综述[J]. 计算机学报, 2017, 40(9): 2070–2092 GUO C X, CHEN H, SUN H, et al. Parallelism of in-memory sorting algorithm on modern hardware[J]. Chinese Journal of Computers, 2017, 40(9): 2070–2092. |
| [7] | HEGARTY J, DALY R, DEVITO Z, et al. Rigel: flexible multi-rate image processing hardware[J]. ACM Transactions on Graphics, 2016, 35(4): 85. |
| [8] | STEWART R, DUNCAN K, MICHAELSON G, et al. RIPL: a parallel image processing language for FPGAs[J]. ACM Transactions on Reconfigurable Technology and Systems, 2018, 11(1): 7. |
| [9] |
赵盼孜, 李彬华, 毛栊哗, 等. 基于现场可编程门阵列的幸运成像算法的实现[J]. 天文研究与技术, 2019, 16(2): 236–243 ZHAO P Z, LI B H, MAO L H, et al. Implementation of lucky imaging algorithm based on FPGA[J]. Astronomical Research & Technology, 2019, 16(2): 236–243. |
| [10] |
毛栊哗, 李彬华, 张西亮, 等. 基于2 m级大口径望远镜的幸运成像算法的实验研究[J]. 光学技术, 2018, 44(5): 542–548 MAO L H, LI B U, ZHANG X L, et al. Experimental investigation of lucky imaging algorithm based on 2 m astronomical telescope[J]. Optical Technique, 2018, 44(5): 542–548. |



