2. 中国科学院高能物理研究所,北京 100049
2. Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
高海拔宇宙线观测站的广角切伦科夫望远镜阵列是以宇宙线观测研究为核心的国家重大科技基础设施[1-3],由18台广角切伦科夫望远镜组成,主要科学目标是测量1013~1018 eV的宇宙线成分和能谱。望远镜通过测量原初宇宙线引发的广延大气簇射中带电粒子产生的荧光或切伦科夫光反推原初宇宙线的能量和成分。为获得准确原初宇宙线能量,我们需要对望远镜接收的光子数进行绝对标定。成像激光雷达标定系统是通过激光光源、激光指向装置、激光接收装置以及其他辅助装置协同工作,实现端到端标定的精密光学标定系统。作为发射端的激光指向受控于三维升降转台,激光器发射的N0个光子进入大气发生瑞利散射和米散射后,有N1个光子被广角切伦科夫望远镜阵列的反射镜接收,在反射镜焦平面的硅光电倍增管阵列上形成激光事例的像。通过比较激光事例的光电子数和N1,实现对望远镜的绝对标定。端到端的激光标定方法对三维升降转台的指向精度要求小于0.05°。
皮埃尔·俄歇天文台(Pierre Auger Observatory)荧光望远镜探测器也采用类似激光标定系统,其激光扫描系统由激光光源和两个正交旋转轴上的镜子组成,可将激光束导向地平线以上包括竖直方向在内的任何方向。垂直光束绝对指向精度为0.04°,扫描绝对指向精度为0.2°、相对指向精度为1/80°[4]。HIRES(High Resolution Fly′s Eye)[5]探测器由HiRes1和HiRes2两台望远镜组成,采用大气荧光技术探测超高能宇宙线。其激光扫描系统由激光器和一系列可旋转的光学镜片组成,绝对指向精度在任意方向均小于0.1°,水平方向相对指向精度为0.03°,俯仰方向相对指向精度为0.005°[6]。高海拔宇宙线观测站运行的两台广角切伦科夫望远镜阵列样机采用的激光扫描系统能够指向水平以上任意方向并保证角度分辨率小于0.1°[7]。
在广角切伦科夫望远镜阵列成像激光雷达标定系统中,由慢控子系统控制三维升降转台,能够精确控制激光束的方向,并且实现全天区自动控制巡航。通过实验测量得到水平方向旋转定位精度、重复精度和空回误差分别为0.005°,0.003°和0.013°;俯仰方向旋转定位精度、重复精度和空回误差分别为0.004°,0.003°和0.087°;升降方向定位精度、重复精度和空回误差分别为0.056 mm,0.075 mm和0.200 mm。实验结果表明,三维升降转台的指向精度满足广角切伦科夫望远镜阵列激光标定和大气监测的需求,也为三维升降转台自动控制巡航准确运行提供依据,结合标准零点监测和校准,保障转台长期稳定运行。
1 设计和构成高海拔宇宙线观测站位于四川省稻城县平均海拔4 410 m的海子山,地处青藏高原的边沿地带,天气变化较快[8]。基于高海拔宇宙线观测站站址的野外自然环境状况和激光标定需求,本文设计了以三维升降转台为重要组成部分的成像激光雷达标定系统。三维升降转台总体布局如图 1,主要由慢控子系统、机械子系统和标准零点子系统3部分组成。

|
| 图 1 三维升降转台总体布局 Fig. 1 The overall layout of 3D rotating and lifting platform |
(1) 慢控子系统实现对三维升降转台可编程式逻辑控制,保证转台稳定执行全天巡航任务,同时将运行状态、周围环境等信息实时存储至本地电脑。Actel FPGA控制芯片驱动控制转台的步进电机工作,并用高精度编码器反馈数值信息以实现闭环控制,将现场可编程门阵列通过RS422连到本地电脑实现远程操控[9]。慢控子系统可支持20种不同自动控制巡航方案,每种方案设置多角度巡航,运行期间可随时切换巡航方案。慢控软件的控制精度小于0.01°,该精度为标准零点自行开发的图像处理软件的精度设置提供依据。
(2) 机械子系统主要包括三维升降转台和翻盖门。三维升降转台主要由可旋转0~360°的水平电动旋转台(图 2(a))、可旋转-10~90°的俯仰电动旋转台(图 2(b))和可平移0~510 mm的电动升降台(图 2(c))组成。水平电动旋转台、俯仰电动旋转台和电动升降台中心承重分别为100 kg,50 kg和45 kg,均用铝合金材料制造。相关信息描述如表 1。自动控制巡航前翻盖门自动打开,巡航结束之后自动关闭,起到保护三维升降转台和激光器的作用。

|
| 图 2 三维升降转台主要机械组成示意图。(a)水平电动旋转台;(b)俯仰电动旋转台;(c)电动升降台 Fig. 2 Schematic diagram of each part of 3D rotating and lifting platform. (a) Horizontal motorized rotational stage; (b) pitch motorized rotational stage; (c) motorized lifting stage |
| Horizontal motorized rotational stage | Pitch motorized rotational stage | Motorized lifting stage | |
| Travel | 0-360° | -10-90° | 510 mm |
| Platform size | r=200 mm | r=100 mm | 400 mm×200 mm |
| Drive mechanism | worm gear | worm gear | high-precision screw bar |
| Guideway form | cross-roller guide | cross-roller guide | slide guide |
| Step motor | SST57D2121 | SST57D2121 | SST57D2121 |
| Encoder | high-precision encoder | high-precision encoder | high-precision encoder |
| Host materials | aluminium alloy | aluminium alloy | aluminium alloy |
| Load capacity/kg | 100 | 50 | 45 |
| Minimum setting | 0.01° | 0.01° | 0.75 μm |
| Gear ratio | 180∶1 | 180∶1 | 1∶25 |
| Maximum speed | 10°/s | 10°/s | 2 mm/s |
(3) 标准零点子系统主要由CCD相机、0.01%衰减片、坐标纸等组成,用于三维升降转台指向的监测和校准。
2 性能研究 2.1 数字图像处理技术为了研究三维升降转台定位精度、重复精度和二维夹角大小等性能,我们采用高精度数字图像处理技术测量其参量。首先,搭建实验平台如图 3(a),将固定在三维升降转台顶部的氦氖激光器(指向稳定且光强呈高斯分布)作为光源,使其光斑打在距离L处的坐标纸上。为了避免光斑图像过曝光和杂散光的影响,CCD相机需要在镜头前放置0.01%衰减片且在暗室内对光斑进行成像。其次,对CCD进行相机定标:通过相机拍照计算图像像素长度与坐标纸物理长度的比值K,单位是μm/pixel,得到坐标纸光斑中心的具体位置,如图 3(b)。从图中可得光斑在横坐标投影下的光强分布,通过高斯函数拟合的平均值确定光斑中心横坐标x,做类似处理可得光斑中心纵坐标。最后,计算三维升降转台转动角度θ:转台转动引起光斑中心位移变化Δx,可通过几何关系公式θ≈KΔx/L计算角位移θ。该技术测量精度同光源与坐标纸距离L,CCD相机与坐标纸距离d,激光光源指向稳定性等因素有关。如图 3(c),当L=214.5 cm,d=35.6 cm时,对153个光斑图像进行处理后,得到水平方向、俯仰方向和升降的测量精度分别为0.000 9°,0.000 9°和0.041 mm,满足三维升降转台设计指标的精度要求。

|
| 图 3 数字图像处理技术原理。(a)实验系统搭建示意图;(b)激光光斑的像和该光斑在横轴投影强度分布(蓝色)及高斯拟合曲线(红色),x轴表示光斑位置在水平方向上的投影,y轴表示对应于x轴处的光斑的强度;(c)激光光斑中心位置在水平方向上的投影的分布 Fig. 3 The principle of digital image processing method. (a) Schematic diagram of experimental system construction; (b) the image of the light spot and the projected intensity distribution of the spot on the horizontal axis (blue) and Gaussian fitting curve (red), x axis represents the position of the laser beam projected in the horizontal direction, and y means the intensity of the laser beam corresponding to the x; (c) the distribution of laser beam position projected in the horizontal direction |
我们使用上述方法对三维升降转台的性能进行测量。用空回误差、定位精度、重复精度和二维夹角等参量表征三维升降转台的性能。测量过程中使用Δθ,Δφ,Δω,Δz和Δz′ 5个变量,其中,Δθ是慢控软件设定的转动角度,Δφ是实际转动角度,Δω是步进电机编码器的反馈值,Δz是慢控软件设定的升降位移,Δz′是实际升降位移。(1)进行三维升降转台的性能测量实验之前,对慢控软件设定的转动角度Δθ(控制步长)进行选择。(2)方法是Δθ=0.01°,Δθ与Δω是否相等?Δθ=0.04°,Δθ与Δω是否相等?其他Δθ=0.15°,0.20°,0.25°,0.30°,0.35°,0.40°,0.45°,0.50°,进行相同操作,Δθ与Δω是否相等?(3)选择标准当Δθ=0.20°时,Δθ=Δω,因而在水平、俯仰方向取Δθ=0.20°作为最小控制步长。当Δθ≥0.2°时,Δθ与Δω两者相等;当Δθ < 0.2°时,由于步进电机丢步或转台惯性等原因造成Δθ与Δω两者不相等。仅当Δθ与Δω相等时,进行三维升降转台性能的研究,因而在水平、俯仰方向取Δθ=0.2°作为最小控制步长,在升降方向取Δz=2 mm作为运动步长。
2.2.1 空回误差慢控软件控制三维升降转台某一维先顺时针转动,然后停止(不做任何操作),再逆时针转动,这个过程齿轮存在一个间隙即空回,反之,也存在空回。如图 4,在慢控软件上设定转动最小控制步长为0.2°,以水平方向慢控软件设定的转动角度Δθ为横坐标,以该方向实际转动角度Δφ为纵坐标,对坐标点做线性拟合。其中P0是拟合直线的截距,P1是拟合直线的斜率,斜率值越接近1,说明Δθ与Δφ一致性越好。图 4(a)中的蓝线是三维升降转台在水平方向逆时针数据点的拟合结果,红线是顺时针数据点的拟合结果,两条拟合线初始值P0之差即空回误差,其值为0.004°;同样得到图 4(b)俯仰方向的空回误差为0.087°;图 4(c)升降方向的空回误差为0.20 mm,运动步长为2 mm。三者的线性关系分别为0.99,0.99和0.99。空回误差是影响三维升降转台指向精度的重要因素之一,在设定自动控制巡航方案时,需要考虑空回误差。

|
| 图 4 三维升降转台空载时空回误差。(a)水平方向;(b)俯仰方向;(c)升降方向 Fig. 4 The backlash of the no-load 3D rotating and lifting platform. (a) Horizontal direction; (b) pitch direction; (c) lifting direction |
重复精度用三维升降转台多次实际转动角度Δφ与其设定角度Δθ的偏差(Δφ-Δθ)分布的标准偏差(Std Dev)表示。在实验中,0(相对位置)为初始设定位置,将三维升降转台转动角度设定为20°或升降设定为40 mm,再回到初始设定位置。实验重复测量29次得到三维升降转台的重复精度。结果如图 5,在水平和俯仰方向重复精度为0.003°;在升降方向重复精度为0.058 mm。三维升降转台的相对指向精度为0.004°,满足实验要求。

|
| 图 5 三维升降转台空载时重复精度。(a)水平方向(0°~20°~0°);(b)俯仰方向(0°~20°~0°);(b)升降方向(215 mm~255 mm~215 mm) Fig. 5 The repeatability of 3D rotating and lifting platform. (a) Horizontal direction (0°-20°-0°); (b) pitch direction (0°-20°-0°); (c) lifting direction (215 mm-255 mm-215 mm) |
定位精度是指三维升降转台多次实际转动角度Δφ与设定角度Δθ偏差的平均值,升降方向类似。本次实验在两种情况下进行测试。第1种情况是大角度转动Δθ=20°,升降方向Δz=40 mm,其定位精度如图 5,水平方向的定位精度为0.005°,俯仰方向的定位精度为0.002°,升降方向的定位精度为0.058 mm。第2种情况是设定三维升降转台在水平和俯仰方向以最小控制步长Δθ=0.2°,升降方向以Δz=2 mm进行测量,在水平方向的定位精度为0.002°,俯仰方向的定位精度为0.002°,升降方向的定位精度为0.022 mm。在设定自动控制巡航方案时,角度应尽可能小,但要大于最小控制步长。
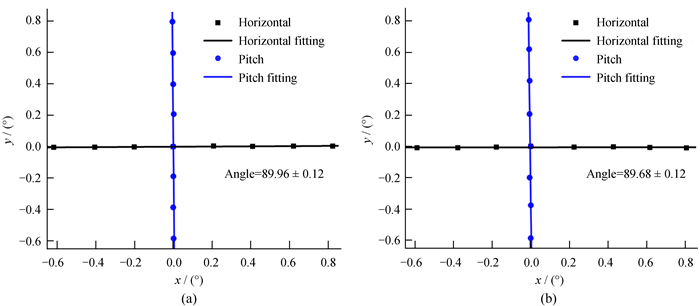
2.2.3 二维夹角在广角切伦科夫望远镜阵列成像雷达激光标定实验中,慢控子系统控制三维升降转台扫描广角切伦科夫望远镜阵列,巡航过程中水平旋转面与俯仰旋转面之间的二维夹角需要精确测量,如果该夹角与90°相差过大,造成水平或者俯仰方向角度偏差加大。我们用数字图像处理技术对三维升降转台空载和负载的情况分别进行测量。保持俯仰角为0°,记录光斑水平方向转动步长为0.2°的轨迹,同样方式得到方位角为0°时俯仰方向的转动轨迹。共同形成的“十字”光斑轨迹如图 6,近似平行于x轴的轨迹即水平旋转面与坐标纸平面的交线,近似平行于y轴的轨迹即俯仰旋转面与坐标纸平面的交线。由于坐标纸平面与水平旋转面和俯仰旋转面均垂直,所以图中轨迹的夹角就是这两个旋转面的夹角。水平与俯仰方向的测量数据拟合可以得到空载情况下二维夹角为89.96°±0.12°(图 6(a)),负载情况下二维夹角为89.68°±0.12°(图 6(b))。将负载情况下的二维夹角值用于激光标定模拟程序。
|
| 图 6 二维夹角测量。(a)空载情况下的二维夹角;(b)负载情况下的二维夹角 Fig. 6 The angle between horizontal and vertical plane. (a) The no-loading two-dimensional angle; (b) the loaded two-dimensional angle |
本次实验测量了学校实验室、高海拔宇宙线观测站站址的L2,L3和L4激光标定实验室里的三维升降转台, 共4台。其中一台的测量结果如表 2,负载(load,大于10 kg)是指三维升降台上的激光器和保温箱。测量结果表明,在有负载的情况下,三维升降转台的精度与空载时保持一致。
| Horizontal direction | Pitch direction | Lift direction | ||||||
| load | no-load | load | no-load | load | no-load | |||
| Method errors/(°/mm) | 0.000 9 | 0.000 9 | 0.000 9 | 0.000 9 | 0.034 | 0.041 | ||
| Repeatability/(°/mm) | 0.002 | 0.002 | 0.001 | 0.003 | 0.075 | 0.005 | ||
| Positional accuracy/(°/mm) (step=0.2) | 0.003 | 0.002 | 0.004 | 0.002 | 0.025 | 0.022 | ||
| Error of back lash/(°/mm) | 0.013 | 0.004 | 0.007 | 0.087 | 0.190 | 0.200 | ||
为确定三维升降转台在地理上的精确指向,我们设置升降指定高度、正北方向和俯仰水平的指向为标准零点,用分度值为0.02 mm/m的水平尺调试激光标定系统中的转台支架和三维升降转台的水平方位:首先将转台支架调节至水平方向,然后从下至上调试三维升降转台,确保俯仰方向的初始方向水平即俯仰角度为0°;用太阳影子法[10]确定地理上的正北方向,并定义正北方向为0°,正东为90°,同时确定三维升降转台水平方向初始角度为0°,升降方向上升60 mm的位置作为升降的初始位置。
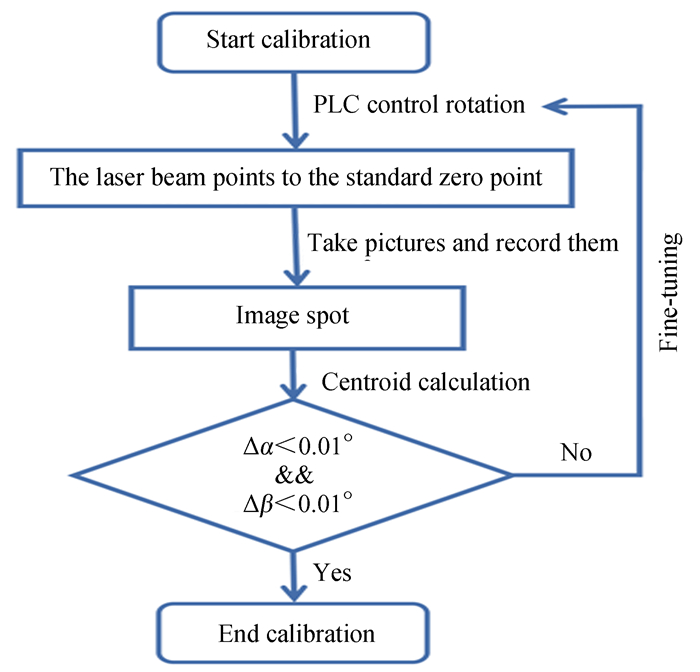
三维升降转台长时间运行可能导致初始指向产生偏差,为避免频繁现场校准,需要搭建一套标准零点监测系统。该系统采用与图 3相同的数字图像处理技术,通过确定激光光斑的位置标定标准零点的位置。系统用氮分子激光器作为光源,通过一款自行开发的图像处理软件实时计算光斑的位置。通过该位置与标准零点位置对比确定三维升降转台初始方向的偏差值。当水平偏差角度Δα小于0.01°,且俯仰偏差角度Δβ小于0.01°时,该位置是标准零点,否则,通过慢控软件微调三维升降转台指向,直至标准零点。标准零点校准和监测流程如图 7。
|
| 图 7 标准零点校准和监测流程 Fig. 7 The process of the standard zero method calibration and monitoring |
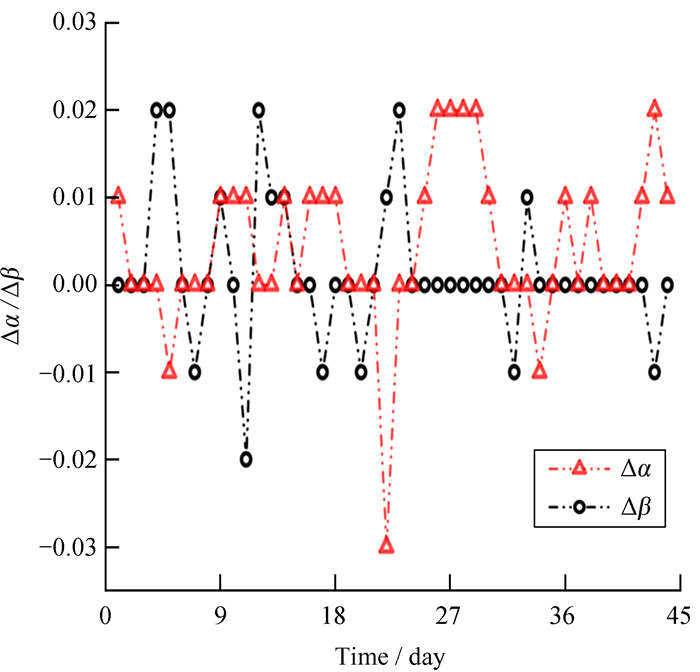
氮分子激光器的光斑位置是20个激光脉冲位置的平均值,由此得到的光斑水平方向的精度为0.004°,俯仰方向的精度为0.000 3°,满足实验要求。标准零点长期的监测结果如图 8,红色三角形代表水平方向的偏差Δα,黑色圆圈代表俯仰方向的偏差Δβ。图 8是连续45天长期监测的结果,其中14天无需进行校零操作,另外31天需要进行标准零点校准。
|
| 图 8 标准零点长期监测 Fig. 8 The long-term monitoring results of standard zero method |
为满足广角切伦科夫望远镜阵列激光标定和大气监测的需求,激光束需要在望远镜阵列运行期间扫描每台望远镜的视场。为解决在长时间、多角度情况下人工控制激光束指向经常出错的问题,我们采用慢控子系统控制三维升降转台的自动控制巡航方案,该方案可实现全自动运行并增加了视场扫描时间。
首先,根据三维升降转台和每台望远镜的位置及指向,确定三维升降转台对每台望远镜标定和监测时所需要的角度。其次,为避免三维升降转台空回误差的影响,巡航方案中的循环转动角度均遵循从小到大的顺序,即先固定一个俯仰角,执行水平方向从小到大扫描,然后至下一个更大的俯仰角度,按照相同方式执行水平方向扫描,以此类推完成一个循环。三维升降转台每转动一个角度需停留一定时间,目的是减少转台转动引起的振动,并给望远镜采集数据预留充足的时间。最后,单次循环时间控制在20 min内,满足大气监测的要求。
为保证每次激光巡航初始指向保持不变,系统需要在自动控制循环前进行标准零点校准和监测。此后,三维升降转台从初始位置升至激光发射位置,开始自动循环。望远镜观测结束之后,自动控制循环结束,三维升降转台回到初始位置,完成巡航。巡航过程中,如遇极端恶劣天气等意外情况,可以随时终止自动巡航。
三维升降转台的定位精度、重复精度和空回误差等性能测量结果保证了转台自动巡航时的指向准确性。
5 结论与展望本文基于广角切伦科夫望远镜阵列的成像激光雷达标定系统指向精度高和自动巡航的需求,设计了三维升降激光转台,提出了数字图像处理技术并以此测量了三维升降转台的性能参量。实验结果表明,三维升降转台的旋转和升降运动定位精度分别为0.005°和0.056 mm,旋转和升降重复精度分别为0.003°和0.075 mm。其定位精度、重复精度和空回误差的测量结果,为慢控子系统自动控制三维升降转台的指向准确性提供了依据。此外,在成像激光雷达标定系统中标准零点校准与监控的应用确保了激光指向的长期精度。
成像激光雷达标定系统中的三维升降转台实现了自动控制,且符合广角切伦科夫望远镜阵列成像激光雷达标定实验的精度要求,保证了望远镜阵列光子数的绝对标定、天气监测、气溶胶的分布等的精确测量,对其他望远镜观测实验具有借鉴意义。
今后,我们将通过对望远镜观测到的激光事例的研究,进一步分析和监测三维升降转台的精度。
| [1] | CAO Z, CHEN M, CHEN S Z, et al. Introduction to Large High Altitude Air Shower Observatory (LHAASO)[J]. Chinese Astronomy and Astrophysics, 2019, 43(4): 457–478. DOI: 10.1016/j.chinastron.2019.11.001 |
| [2] |
纪方, 张健欣, 陈明君, 等. 基于WCDA水质监测分析[J]. 天文研究与技术, 2020, 17(2): 252–257 JI F, ZHANG J X, CHEN M J, et al. Water quality monitoring analysis based on WCDA[J]. Astronomical Research & Technology, 2020, 17(2): 252–257. |
| [3] |
吴文雄, 左雄, 肖刚, 等. LHAASO-MD光电倍增管的性能测试[J]. 天文研究与技术, 2020, 17(2): 258–264 WU W X, ZUO X, XIAO G, et al. The performance test of LHAASO-MD photomultiplier[J]. Astronomical Research & Technology, 2020, 17(2): 258–264. |
| [4] | FICK B, MALEK M, MATTHEWS J A J, et al. The Central Laser Facility at the Pierre Auger Observatory[J]. Journal of Instrumentation, 2006, 1: P11003. DOI: 10.1088/1748-0221/1/11/P11003 |
| [5] | ABU-ZAYYAD T, AL-SEADY M, BELOV K, et al. The prototype high-resolution Fly's Eye cosmic ray detector[J]. Nuclear Instruments & Methods in Physics Research A, 2000, 450(2): 253–269. |
| [6] | WIENCKE L R, GRAY R C, MUMFORD J R, et al. Steerable laser system for UV atmospheric monitoring at the High-Resolution Fly's Eye[C]// Proceedings of SPIE. 1999. |
| [7] | LIU J L, ZHU F R, JIA H Y, et al. A calibration of WFCTA prototype telescopes using N2 laser[J]. Nuclear Instruments & Methods in Physics Research A, 2018, 877: 278–287. |
| [8] | PI W X, HUANG M, ZHU F R, et al. Extinction coefficients of surface atmospheric aerosol above LHAASO[J]. Chinese Physics C, 2019, 43(8): 117–123. DOI: 10.1088/1674-1137/43/8/085001 |
| [9] | YE W R, SUN Z B, GENG B M. Three freedom degrees precision laser turntable control system based on FPGA[J]. Electronic Design Engineering, 2014, 22(11): 15–18. |
| [10] | 吕洪魁. LHAASO-KM2A电磁粒子探测器大动态范围设计及阵列的标定研究[D]. 北京: 中国科学院大学, 2016. LYU H K. Calibration of LHAASO-KM2A and a large dynamic range design for the electromagnetic particle detectors[D]. Beijing: University of Chinese Academy of Sciences, 2016. |



