2. 中国科学院射电天文重点实验室,江苏 南京 210033;
3. 新疆射电天体物理重点实验室,新疆 乌鲁木齐 830011;
4. 中国科学院大学,北京 100049
2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
3. Key Laboratory of Xinjiang Radio Astrophysics, Urumqi 830011, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
因长期磨损和扭转等原因而产生的射电望远镜天线俯仰轴形变,虽然变化量不大,但对高精度指向产生的影响不可忽略。这种影响随着天线口径增大、观测频段提高、天线综合性能要求提升而更加明显。研究俯仰轴形位变化对提高望远镜指向精度具有重要意义[1-2]。
国内外学者对于大口径、高精度天线的关键结构变化对性能影响的研究主要集中在大中尺度变形的测量及补偿。如美国绿岸望远镜(Green Bank Telescope, GBT)[3]在天线座架及副面撑腿上安装了温度传感器,测量结构受温度影响的大小。文[4-6]考虑天线结构阴影遮挡,对500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope, FAST)及上海天马65 m射电望远镜进行了热力学仿真,分析了各类天线的温度分布特性。意大利撒丁岛射电望远镜(Sardinia Radio Telescope, SRT)利用位置传感器测量副反射体位姿,用于修正副面因自重、环境载荷造成的位置偏差[7-8]。上海天马65 m射电望远镜利用位置传感器测量副面三维位移,并分析各种因素导致的大型射电望远镜的副面位姿变化[9-10]。文[11]利用倾斜仪、热电偶和风速仪建立方位轴误差和温度梯度以及方位轴误差和风载倾覆力矩之间的经验公式。文[12]测量了新疆南山26 m射电望远镜的轨道高差,并分析了其对指向精度的影响。然而,对于天线重要部件的小尺度变形测量研究并不多。文[13]为RT-70 Suffa(Radio Telescope-70 Suffa)射电望远镜俯仰轴设计了基于自准直方法的角度变形测量系统,在22 m的测量距离和16′测量范围内,系统误差为15′。改进后的自准直法测量系统的测量距离为8 m,其精度均方根(Root Mean Square, RMS)为11″ [14]。但是自准直法系统结构复杂,安装要求高,不易维护。
作为天线结构的重要部件,俯仰轴因为长期运行过程中的磨损和扭转等原因,会发生小尺度形变。这将导致轴角编码器获取的俯仰角和实际值产生偏差,影响射电望远镜指向精度,而且由于微小形变引起的内部组织性能演化将加速俯仰轴疲劳。快速高精度测量俯仰轴的形变为天线指向误差修正、俯仰轴系统主动维护以及制定和调整望远镜观测计划提供重要支撑。
本文设计了一种单相机形变测量系统,建立了虚拟相机数学模型,通过快速获取并处理靶标图像分析靶标处俯仰轴形变情况,实现俯仰轴结构小尺度变形的快速高精度测量,为实现大口径射电望远镜指向精度修正提供一种备选方法。
1 单相机形变测量系统单相机形变测量系统如图 1(a)。靶标固定在俯仰轴上,根据靶标图像获取俯仰轴的形变信息。每个靶标对应某一俯仰角下的俯仰轴情况,例如靶标1,2和3分别在俯仰轴30°,60°和90°时唯一出现在相机视野中并被拍摄图像。本文约定分别沿着x, y和z轴正向以右手法则为俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll),如图 1(b)。
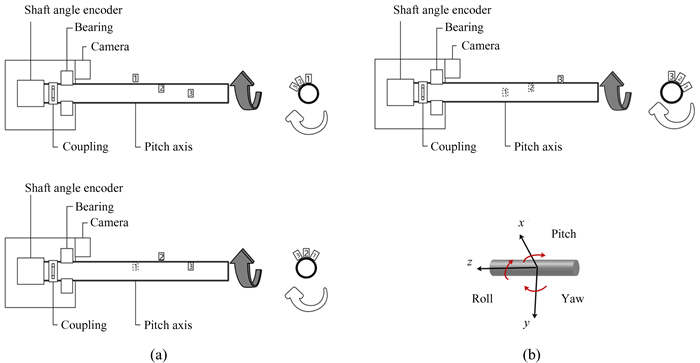
|
| 图 1 单相机形变测量系统及俯仰轴角度方向 Fig. 1 Single camera deformation measurement system and angular orientation of the pitch axis |
测量原理是通过靶标位置与参考位置对比,求解俯仰轴在不同俯仰角下的变换。首先,在俯仰轴非工作时,获取靶标参考位置;然后在俯仰轴正常工作时,转到俯仰角30°时,固定在俯仰轴末端的相机快速获取靶标1图像;最后,通过靶标1的图像集,得到俯仰角30°时俯仰轴局部的变化情况。
2 测量系统数学模型 2.1 虚拟相机虚拟相机是将真实物体空间变换等效成真实相机空间变换的方法,特点是在真实相机中观察到的物体运动情况与虚拟相机中原物体运动情况一致。虚拟相机的优势在于一个固定相机能够监测物体的小尺度六自由度运动情况,且虚拟相机空间变换与真实物体空间变换有定量关系。
本文假定真实模型包括初始目标A、形变后的目标B和真实相机O,如图 2(a);虚拟模型包括初始目标A、真实相机O和虚拟相机P,如图 2(b)。建立右手坐标系,O-xOyOzO为真实相机坐标系,也是世界坐标系;A-xAyAzA为初始目标坐标系,目标坐标系各坐标轴与真实相机坐标系平行;B-xByBzB为形变后的目标坐标系;P-xPyPzP为虚拟相机坐标系。
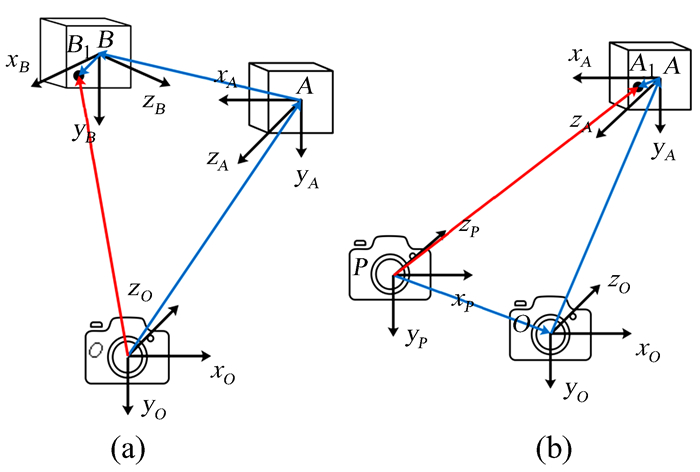
|
| 图 2 真实模型与虚拟模型。(a)真实模型;(b)虚拟模型 Fig. 2 Real and virtual models. (a) Real model; (b) virtual model |
假设存在一个虚拟相机P,当俯仰轴上目标A变化到B,虚拟相机拍摄的目标A图像与真实相机O拍摄的目标B的图像完全相同,则
| $ {\overrightarrow{O B_{1}}}={\overrightarrow{P A_{1}}} $ | (1) |
成立,其中A1和B1分别为A-xAyAzA和B-xByBzB目标上同一点,如图 2。
在O-xOyOzO和P-xPyPzP坐标系中,
| $ \begin{aligned} &\overrightarrow{O B_{1}}=\overrightarrow{O A}+{ }_{A}^{0} \boldsymbol{R} \overrightarrow{A B}+{ }_{A}^{0} \boldsymbol{R}_{B}^{A} \boldsymbol{R} \overrightarrow{B B_{1}}, \\ &\overrightarrow{P A_{1}}=\overrightarrow{P O}+{ }_{0}^{P} \boldsymbol{R} \overrightarrow{O A}+{ }_{0}^{P} \boldsymbol{R}_{A}^{o} \boldsymbol{R} \overrightarrow{A A_{1}}. \end{aligned} $ | (2) |
根据虚拟相机的概念以及(1)式和(2)式,目标空间变换可等价为虚拟相机相对于真实相机的空间变换。
2.2 空间等价变换由于虚拟相机的存在,若目标A平移变换到B,则相当于真实相机O平移到虚拟相机P,如图 3(a)。若目标A旋转变换到B,则相当于真实相机O先平移到虚拟相机P,再旋转到Q,如图 3(b)。一次空间变换,等价于若干次平移变换和旋转变换的组合迭代。
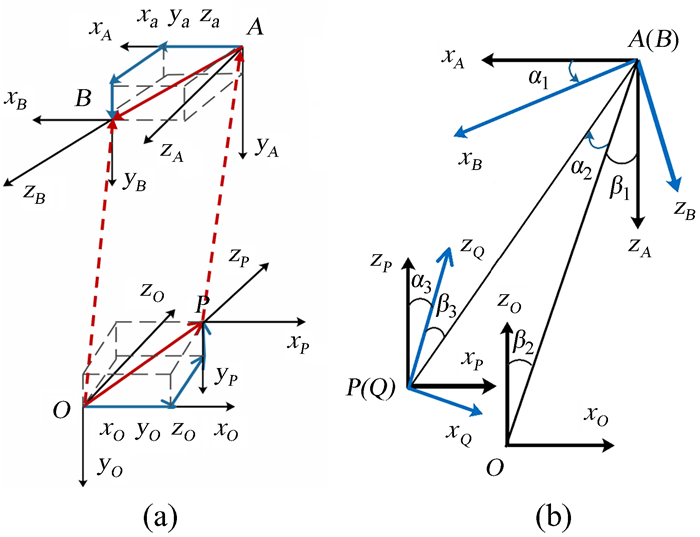
|
| 图 3 目标的平移与旋转。(a)平移变换;(b)旋转变换 Fig. 3 Translation and rotation of the target. (a) Translational transformation; (b) rotational transformation |
在图 3(a)中, 平移变换的关系为
| $ \begin{gathered} \overrightarrow{O B}=\overrightarrow{P A}, \\ x_{a}=x_{o}, y_{a}=-y_{o}, z_{a}=z_{o}. \end{gathered} $ | (3) |
在图 3(b)中,旋转变换的关系为
| $ \begin{gathered} \overrightarrow{P A}=\overrightarrow{O B}, \\ \alpha_{1}=\alpha_{2}=\alpha_{3}, \\ \beta_{1}=\beta_{2}=\beta_{3}. \end{gathered} $ | (4) |
根据坐标系的欧氏变换,可以得到目标空间等价变换定量关系。设某个向量在A-xAyAzA中表示为
| $ \begin{array}{l} \vec{b}={ }_{A}^{o} \boldsymbol{R} \overrightarrow{a}+\boldsymbol{t}_{O A}, \\ \vec{b}={ }_{B}^{o} \boldsymbol{R}\left({ }_{A}^{B} \boldsymbol{R} \overrightarrow{a}+\boldsymbol{t}_{B A}\right)+\boldsymbol{t}_{O B}, \\ \vec{b}={ }_{P}^{0} \boldsymbol{R}\left({ }_{A}^{P} \boldsymbol{R} \overrightarrow{a}+\boldsymbol{t}_{P A}\right)+\boldsymbol{t}_{O P} \end{array} $ | (5) |
成立。由(5)式可以得
| $ { }_{A}^{O} \boldsymbol{T}={ }_{B}^{0} \boldsymbol{T}_{A}^{B} \boldsymbol{T}={ }_{P}^{O} \boldsymbol{T}_{A}^{P} \boldsymbol{T}, $ | (6) |
其中,
| $ { }_{A}^{O} \boldsymbol{T}=\left|\begin{array}{cc} { }_{A}^{O} \boldsymbol{R} & \boldsymbol{t}_{O A} \\ 0^{\mathrm{T}} & 1 \end{array}\right|, { }_{B}^{O} \boldsymbol{T}=\left|\begin{array}{cc} { }_{B}^{O} \boldsymbol{R} & \boldsymbol{t}_{O B} \\ 0^{\mathrm{T}} & 1 \end{array}\right|, { }_{A}^{B} \boldsymbol{T}=\left|\begin{array}{cc} { }_{A}^{B} \boldsymbol{R} & \boldsymbol{t}_{B A} \\ 0^{\mathrm{T}} & 1 \end{array}\right|, { }_{P}^{O} \boldsymbol{T}=\left|\begin{array}{cc} { }_{P}^{O} \boldsymbol{R} & \boldsymbol{t}_{O P} \\ 0^{\mathrm{T}} & 1 \end{array}\right|, { }_{A}^{P} \boldsymbol{T}=\left|\begin{array}{cc} { }_{A}^{P} \boldsymbol{R} & \boldsymbol{t}_{P A} \\ 0^{\mathrm{T}} & 1 \end{array}\right|, $ |
AOT为系统固有矩阵,与真实固定相机和初始目标的相对位置有关;BOT为O-xOyOzO到B-xByBzB的变换;BOT为目标空间变化量;POT为虚拟相机变化量;APT为A-xAyAzA到P-xPyPzP的变换。容易得出BOT=APT,故目标空间变换关系为
| $ {}_A^B\boldsymbol{T} = _A^O{\boldsymbol{T}^{ - 1}}_P^O\boldsymbol{T}_A^O\boldsymbol{T}, $ | (7) |
其中,AOT可由(2)式求得。
3 虚拟相机空间变换求解 3.1 相机模型理想相机可以看作是针孔相机,如图 4。设OC-xCyCzC为相机坐标系,OW-xWyWzW为世界坐标系,OUV-UV为图像像素坐标系。设点P在世界坐标系中的坐标为(xW, yW, zW),在相机坐标系中的坐标为(xC, yC, zC),成像点P0像素坐标为(u, v),相机成像过程表示为
| $ {Z_C}\left( {\begin{array}{*{20}{l}} u\\ v\\ 1 \end{array}} \right) = \boldsymbol{K}\left( {\begin{array}{*{20}{l}} {{x_C}}\\ {{y_C}}\\ {{z_C}}\\ 1 \end{array}} \right) = \boldsymbol{KM}\left( {\begin{array}{*{20}{l}} {{x_W}}\\ {{y_W}}\\ {{z_W}}\\ 1 \end{array}} \right), $ | (8) |
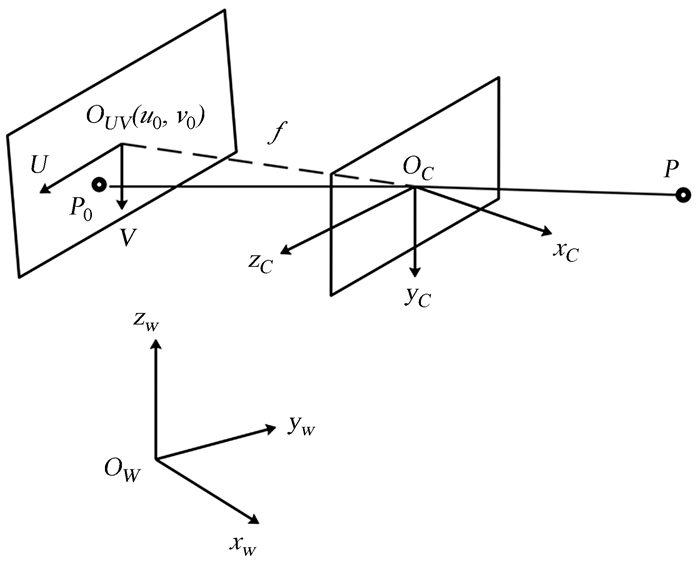
|
| 图 4 针孔相机模型 Fig. 4 Pinhole camera model |
其中,K为相机内参矩阵,
实际相机模型有多种类型畸变,但一般情况下考虑径向畸变和切向畸变已经足够。
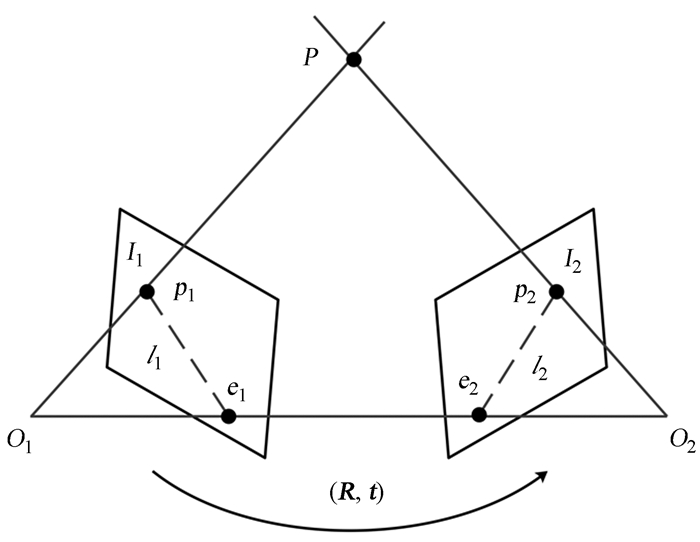
3.2 第1帧对应虚拟相机空间变换利用二维投影求解第1帧对应虚拟相机空间变换[15],如图 5。设P是三维空间中一点,O1和O2是真实相机光心和虚拟相机光心,空间变换为R和t,p1和p2分别是空间点P在两个成像平面I1和I2上的投影,l1和l2是极线,e1和e2是极点。根据针孔相机模型得
| $ s_{1} p_{1}=\boldsymbol{K} P, s_{2} p_{2}=\boldsymbol{K}(\boldsymbol{R} P+\boldsymbol{t}), $ | (9) |
|
| 图 5 参考帧和第1帧的关系 Fig. 5 The relationship between the reference frame and the first frame |
其中,K为相机内参矩阵;s1和s2为特征点深度。若取x1和x2是两个像素点的归一化平面坐标,得到
| $ x_{2}{ }^{\mathrm{T}} \boldsymbol{E} x_{1}=p_{2}{ }^{\mathrm{T}} \boldsymbol{F} p_{1}=0, $ | (10) |
其中,x1=K-1p1, x2=K-1p2;F为基础矩阵;E为本质矩阵。分解E或F可求R和t,若多对空间点都落在同一平面内,则通过单应矩阵H求R和t。
3.3 其余帧对应虚拟相机空间变换利用三角测量法公式
| $ s_{2} x_{2}=s_{1} \boldsymbol{R} x_{1}+\boldsymbol{t} $ | (11) |
得到空间点的深度信息。
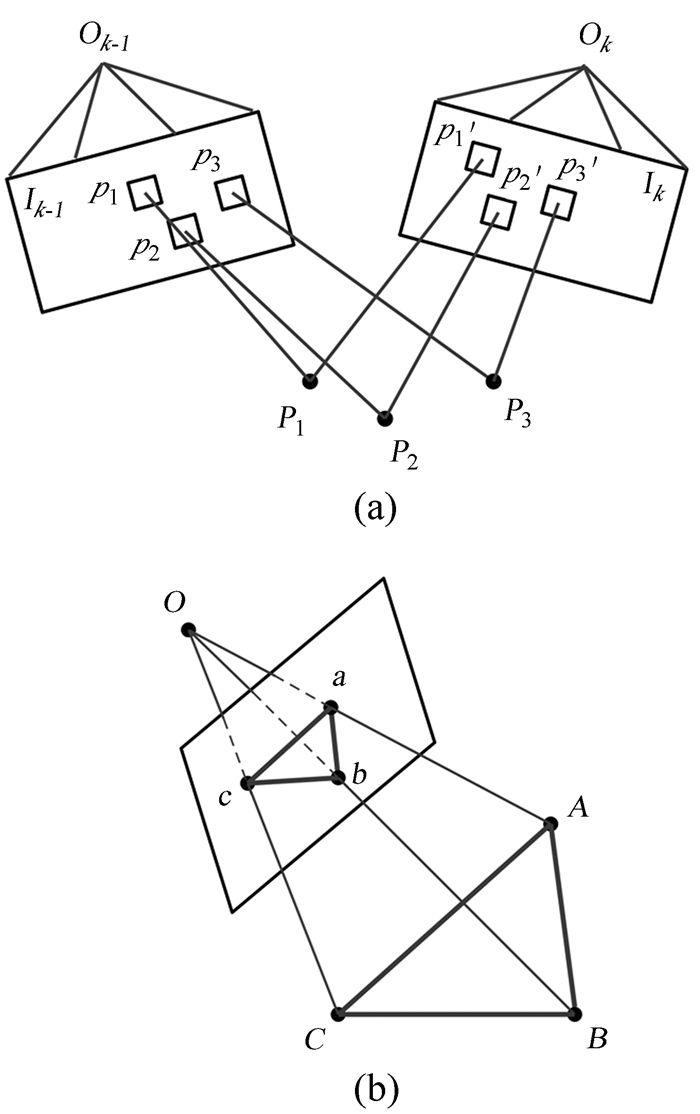
从第2帧起,相邻帧间的关系如图 6(a),Ok-1和Ik-1是前一帧对应虚拟相机的光心和图像;Ok和Ik是当前帧对应虚拟相机的光心和图像;P1,P2和P3是空间点;p1,p2和p3,以及p′1,p′2和p′3是投影点。
|
| 图 6 其余帧虚拟相机空间变换。(a)相邻帧的关系;(b)P3P Fig. 6 Virtual camera space transformation for the remaining frames. (a) Relationship between adjacent frames; (b) P3P |
根据多个空间点三维信息和相邻帧间的关系,借助P3P(Perspective-3-Points)[16]求解其余帧对应虚拟相机空间变换,如图 6(b)。空间点A, B和C分别对应图像投影点a, b和c,几何关系表示为
| $ \begin{aligned} &O A^{2}+O B^{2}-2 O A \;\;O B \cos \langle a, b\rangle=A B^{2}, \\ &O B^{2}+O C^{2}-2 O B \;\;O C \cos \langle b, c\rangle=B C^{2}, \\ &O A^{2}+O C^{2}-2 O A \;\;O C \cos \langle a, c\rangle=A C^{2} . \end{aligned} $ | (12) |
本文搭建光学测试平台,验证虚拟相机数学模型中的空间等价变换,并分析当前测试系统下每个自由度的测量误差。
4.1 光学测试平台测试系统主要有空间高精度平台、定焦镜头、相机和标定板等组成,如图 7和表 1。

|
| 图 7 光学测试平台 Fig. 7 Optical test platform |
| Products | Parameters | |
| High-precision four-degree-of-freedom stage | 2*GCD-302001M, GCD-301101M, GCD-012100M | GCD-302001M long reach table with 400 mm stroke and 0.001 25 mm resolution; GCD-301101M lift table with 12 mm stroke and 2.5 mium resolution; GCD-012100M rotary table with 0.000 5 degree resolution |
| Fixed focal lens | AZURE-NV5020M6M | length 50 mm for focal length F2.0-16 for aperture |
| Camera | DMK 33UX290-USB3.0 | The resolution is up to 1 920 × 1 080 with 1/2.8inch, 2.9 mium pixels both horizontally and vertically, and the sensor is Sony IMX290LLR |
| Calibration plate | GCG-020303 | 2.0 mm × 2.0 mm, 25 × 25 arrays |
本次结果分析将图像解算的空间变换数据作为测量值,将高精度四自由度平台数据作为真实值,将测量值与真实值的差作为误差,分析各自由度误差情况。
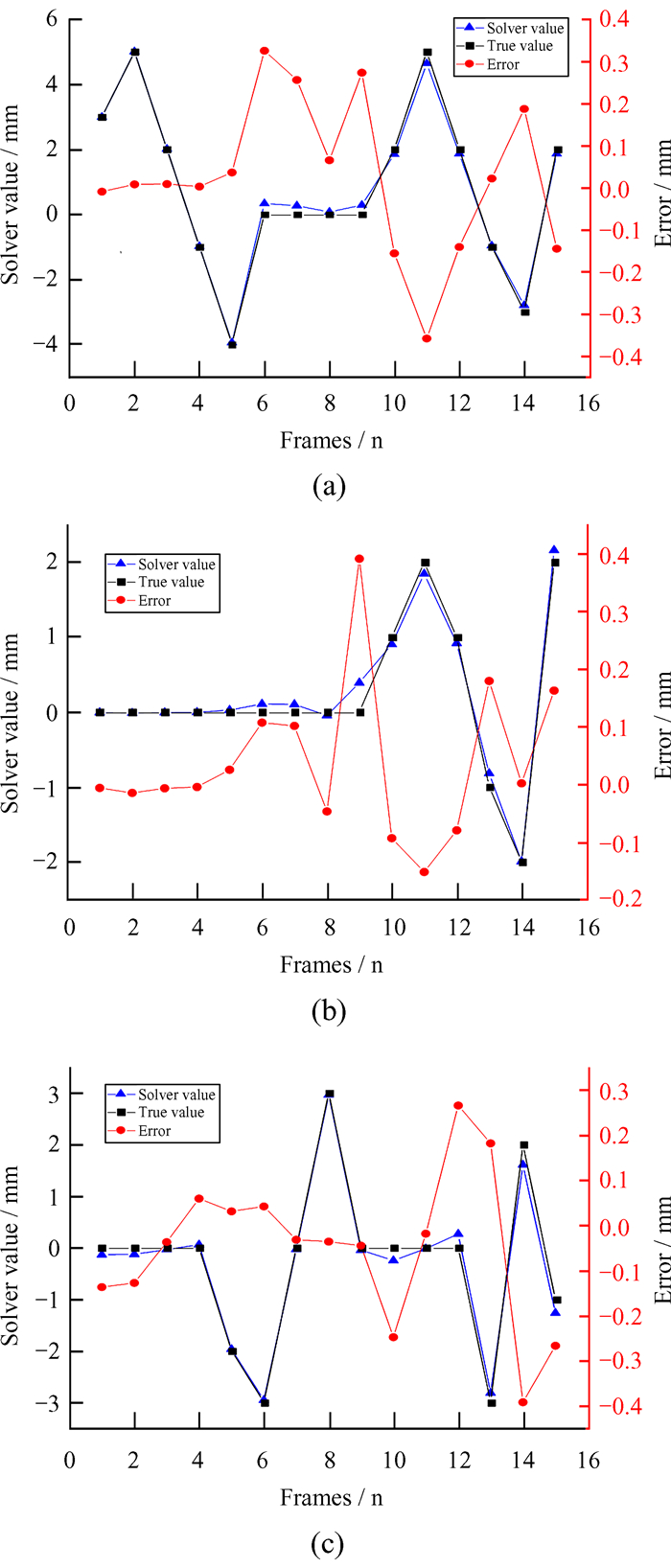
由于结构为小变形量,本次实验平移分量的实验条件是x,y和z方向的变化范围分别为-4~5 mm,-2~2 mm和-3~3 mm。由图 8和表 2可知,平移分量中,x轴方向最大误差为-0.360 2 mm,均方根误差(Root Mean Square Error, RMSE)为0.179 5 mm;y轴方向最大误差为0.391 4 mm,均方根误差为0.135 5 mm;z轴方向最大误差为-0.393 7 mm,均方根误差为0.171 0 mm。
|
| 图 8 平移分量实验结果误差分布图,误差折线反映15帧图像的空间变换在各轴(x, y和z轴)分量测量值与真实值的差值变化。(a)x轴平移分量;(b)y轴平移分量;(c)z轴平移分量 Fig. 8 Error distribution of experimental results for translational components, the error polyline reflects the change of the difference between the measured values and the real values of each axis (x, y and z axes) of the spatial transformation of 15 frames of images. (a) x-axis translational component; (b) y-axis translational component; (c) z-axis translational component |
| Error | x axis | y axis | z axis |
| Minimum/mm | 0.007 1 | 0.001 0 | -0.019 0 |
| Maximum/mm | -0.360 2 | 0.391 4 | -0.393 7 |
| RMS | 0.179 5 | 0.135 5 | 0.171 0 |
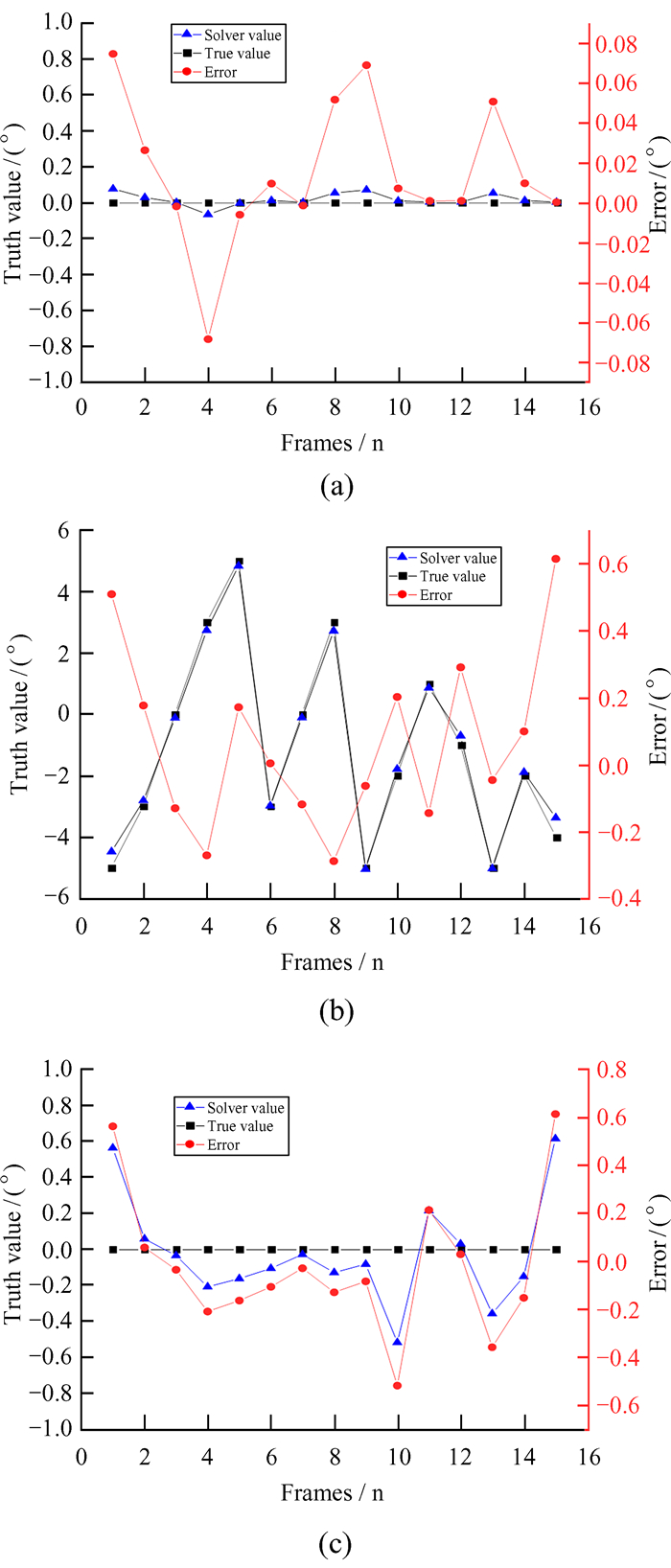
在旋转分量的实验条件为俯仰角和滚转角方向为0,偏航角方向的变化范围为-5~5°。由图 9和表 3可知,旋转分量中,俯仰角方向最大误差为0.074 5°,均方根误差为0.037 6°;偏航角方向最大误差为0.613 8°,均方根误差为0.267 6°;滚转角方向最大误差为0.613 1°,均方根误差为0.291 8°。
|
| 图 9 旋转分量实验结果误差分布图,误差折线反映15帧图像的空间变换的各角(俯仰角、偏航角和滚转角)分量测量值与真实值的差值变化。(a)俯仰角旋转分量;(b)偏航角旋转分量;(c)滚转角旋转分量 Fig. 9 Error distribution of experimental results for rotational components, the error polyline reflects the difference between the measured values and the real values of each angle (pitch angle, yaw angle and roll angle) component of the spatial transformation of 15 frames of images. (a) Pitch angle rotational component; (b) yaw angle rotational component; (c) roll angle rotational component |
| Error | Pitch | Yaw | Roll |
| Minimum/(°) | 0.000 0 | 0.002 3 | 0.031 1 |
| Maximum/(°) | 0.074 5 | 0.613 8 | 0.613 1 |
| RMS | 0.037 6 | 0.267 6 | 0.291 8 |
本文设计了一种单相机俯仰轴形变测量系统,建立了虚拟相机数学模型,提出了一种基于虚拟相机的俯仰轴形变测量方法,并搭建了光学测试平台对所提方法和主要原理进行验证,分析了六自由度误差情况。
实验结果表明,平移分量中,x方向-4~5 mm内均方根误差为0.179 5 mm,y方向-2~2 mm内均方根误差为0.135 5 mm,z方向-3~3 mm内均方根误差为0.171 0 mm;旋转分量中,偏航角方向在俯仰轴旋转-5~5°内均方根误差为0.267 6°,俯仰角方向和滚转角方向在0°处均方根误差分别为0.037 6°与0.291 8°。误差主要由相机坐标轴与靶标坐标轴不完全平行和图像解算方法等因素引起。
该系统及方法具有非接触、精度高、速度快等优点,能满足大口径、高频段、高精度射电望远镜俯仰轴长期快速测量的需求,也适用于其他大结构的小变形测量。
| [1] |
王娜. 新疆奇台110米射电望远镜[J]. 中国科学: 物理学力学天文学, 2014, 44(8): 783–794 WANG N. Xinjiang Qitai 110 m radio telescope[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2014, 44(8): 783–794. |
| [2] |
魏善祥, 王启明, 孔德庆, 等. 大型双反射面天线指向误差评估算法[J]. 天文研究与技术, 2020, 17(4): 513–521 WEI S X, WANG Q M, KONG D Q, et al. Algorithm for estimating pointing error of large dual-reflector antenna[J]. Astronomical Reasearch & Technology, 2020, 17(4): 513–521. DOI: 10.3969/j.issn.1672-7673.2020.04.012 |
| [3] | PRESTAGE R M. The GBT precision telescope control system[C]// Proceedings of SPIE. 2004. |
| [4] |
钱宏亮, 钟杰, 范峰. 上海65 m射电望远镜天线结构日照非均匀温度场[J]. 土木工程学报, 2014, 47(3): 39–46 QIAN H L, ZHONG J, FAN F. Analysis on non-uniform temperature field due to sunshine for the antenna structure of Shanghai 65-meter-aperture radio telescope[J]. China Civil Engineering Journal, 2014, 47(3): 39–46. |
| [5] |
金晓飞, 范峰, 沈世钊. 巨型射电望远镜(FAST) 反射面支承结构日照温度场效应分析[J]. 土木工程学报, 2008(11): 71–77 JIN X F, FAN F, SHEN S Z. Effect of non-uniform temperature field under sunshine on the structure supporting the reflector of a large radio telescope-FAST[J]. China Civil Engineering Journal, 2008(11): 71–77. DOI: 10.3321/j.issn:1000-131X.2008.11.011 |
| [6] | QIAN H, CHEN D, FAN F, et al. Evaluation of solar temperature field under different wind speeds for Shanghai 65 m radio telescope[J]. International Journal of Steel Structures, 2016, 16(2): 383–393. DOI: 10.1007/s13296-016-6011-3 |
| [7] | PISANU T, BUFFA F, DEIANA G L, et al. Architecture of the metrology for the SRT[C]// Proceedings of SPIE. 2012. |
| [8] | PISANU T, BUFFA F, CONCU R, et al. A PSD (position sensing device) to map the shift and tilt of the SRT secondary mirror[C]// Proceedings of SPIE. 2014. |
| [9] |
江永琛, 王锦清, 苟伟, 等. PSD法测量大型射电望远镜副面位姿[J]. 天文学报, 2019, 60(6): 98–107 JIANG Y C, WANG J Q, GOU W, et al. The measurement of sub-reflector's displacement of large radio telescopes by PSD method[J]. Acta Astronomica Sinica, 2019, 60(6): 98–107. |
| [10] | JIANG Y C, WANG J Q, GOU W, et al. A position sensing device's application on TianMa radio telescope[C]// Proceedings of the 17th IEEE International Conference on Communication Technology. 2017. |
| [11] | UKITA N, EZAWA H, IKENOUE B, et al. Thermal and wind effects on the azimuth axis tilt of the ASTE 10-m antenna[J]. Publications of the National Astronomical Observatory of Japan, 2007, 10: 25–33. |
| [12] |
温浩兴, 许谦, 王娜. 南山26米射电望远镜轨道高差测量及其对指向精度的影响[J]. 天文研究与技术, 2019, 16(2): 158–166 WEN H X, XU Q, WANG N. Measurement of NSRT 26 m antenna track unevenness and Influence on pointing accuracy[J]. Astronomical Reasearch & Technology, 2019, 16(2): 158–166. |
| [13] | KONYAKHIN I A, TIMOFEEV A N, USIK A A, et al. Optic-electronic systems for measuring the angle deformations and line shifts of the reflecting elements at the rotateable radio-telescope[C]// Proceedings of SPIE. 2011. |
| [14] | KONYAKHIN I, KOPYLOVA T V, KONYAKHIN A I, et al. Optic-electronic systems for measurement the three-dimension angular deformation of axles at the millimeter wave range radiotelescope[C]// Proceedings of SPIE. 2013. |
| [15] | HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. 2nd ed. New York: Cambridge University Press, 2004. |
| [16] | GAO X S, HOU X R, TANG J L, et al. Complete solution classification for the perspective-three-point problem[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2003, 25(8): 930–943. |



