2. 中国科学院新疆天文台,新疆 乌鲁木齐 830011;
3. 中国科学院射电天文重点实验室,江苏 南京 210033;
4. 新疆射电天体物理重点实验室,新疆 乌鲁木齐 830011
2. Xinjiang Astronomical Observatory, Chinese Academy of Sciences, Urumqi 830011, China;
3. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
4. Key Laboratory of Xinjiang Radio Astrophysics, Urumqi 830011, China
随着科学技术的发展,射电望远镜观测技术取得了长足的进步,极大地推动了天文学的发展。与此同时,大型双反射面天线的口径、频段也在不断增加,对天线的指向精度、增益等指标要求越来越高[1]。天线副面位置与主面位置的匹配对天线指向精度起着至关重要的作用。但在天线运行过程中,副反射面的位置受到风荷、重力、温度等因素的影响发生变化,导致主副面位置匹配失调,天线的综合性能下降,对天线的效率及指向精度产生影响[2]。因此,如何快速、实时、准确地重构天线副面位置,对提高天线指向精度有十分重要的意义。为获得高精度的天线副面位置,文[3]推导并仿真了副面位姿和全息口径面相位的解析关系,通过口径面相位数据,计算获得上海天马65 m射电望远镜副面位姿随俯仰角的变化情况。文[4]基于应变传感器和模态叠加原理,分别通过采集天线发生变形后副反射面撑腿、副反射面自身应变值重构了副反射面的位姿。文[5]采用摄影测量对天线副面随俯仰角的位置变化进行测量,获得了x, y和z方向的位置变化曲线,该方法获取数据量较大,对计算系统要求较高,不能获取天线副面的实时位置。文[6-7]采用位置传感器测量了天线副面随俯仰角变化在x和y方向产生的位置变化,该方法可以获取天线副面在x和y方向的高精度位置,但在z方向的位置需要通过其他方法来获得。文[8]采用激光跟踪仪测量了副面调整机构在0°和45°时副面的位姿情况,该方法具有较高的精度,在对天线副面调整机构的高精度标定中起到很好的作用,但代价太大。文[9]基于惯性测量和嵌入式技术,解决了大型射电望远镜副面摆动较大,无法精确定位的问题,但该方法使用惯性测量技术,会造成误差累积,系统误差越来越大,需要及时调整。
本文采用虚拟双目测量系统,对天线副面在空间移动过程中的三维位置进行模拟测量,得出目标物体在空间运动的三维运动曲线。该方法只需要对目标物体进行一次拍摄,就可以获得副面在该位置的三维信息,不需要很复杂的程序,同时不会造成误差累积。该方法不仅能节约成本,而且能够解决双目视觉左右相机同步难的问题。
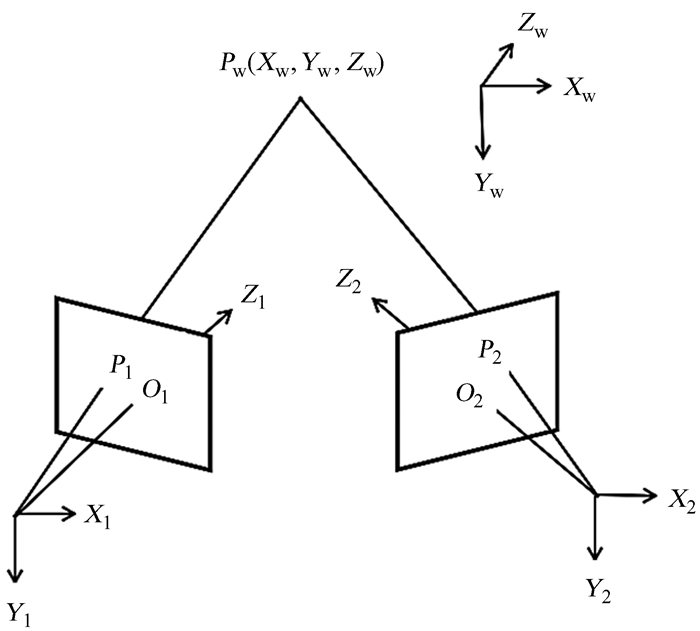
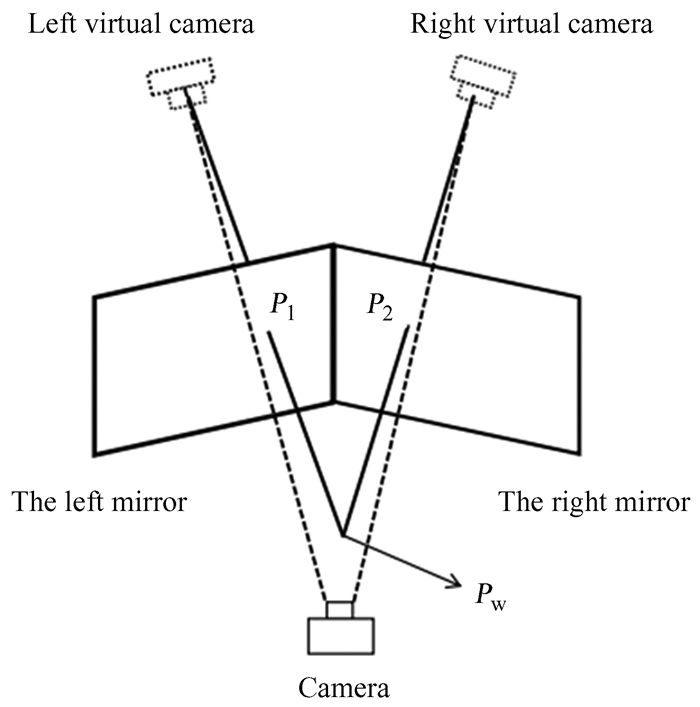
1 虚拟双目视觉原理交汇式双目视觉是基于同一物体在两图像中的视差以及两相机之间的平移和旋转关系,对物体空间三维位置进行求解[10],原理如图 1。为降低成本,提高拍摄同步性,我们使用两个平面镜与一台高速相机组成虚拟双目视觉系统。该方法与交汇式双目视觉原理基本相同,如图 2。
|
| 图 1 交汇式双目视觉原理 Fig. 1 The principle of convergent binocular vision |
|
| 图 2 虚拟双目视觉原理 Fig. 2 The principle of virtual binocular vision |
如图 2,P(x, y, z)为空间任意一点,分别在左右镜面上成像, 高速相机对左右镜面上的像进行拍摄,对拍摄图像进行分割,得到两幅关于点P(x, y, z)的像,相当于有两台虚拟相机对点P(x, y, z)进行拍摄。分析方法与真实双目视觉分析方法基本相同[10]。
Ow-XwYwZw为世界坐标系,O1-X1Y1Z1为左相机摄像机坐标系,O2-X2Y2Z2为右相机摄像机坐标系。P1点为空间点Pw在左相机所成像中的像点,P2点为空间点Pw在右相机所成像中的像点。双目视觉测量中,世界坐标系与摄像机坐标系的关系为
| $ \begin{aligned} z_{c}\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right] &=\left[\begin{array}{ccc} 1 / \mathrm{d} x & 0 & u_{0} \\ 0 & 1 / \mathrm{d} y & v_{0} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{T} \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x_{\mathrm{w}} \\ y_{\mathrm{w}} \\ z_{\mathrm{w}} \\ 1 \end{array}\right] \\ &=\left[\begin{array}{cccc} f / \mathrm{d} x & 0 & u_{0} & 0 \\ 0 & f / \mathrm{d} y & v_{0} & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{T} \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x_{\mathrm{w}} \\ y_{\mathrm{w}} \\ z_{\mathrm{w}} \end{array}\right]\left[\begin{array}{ll} \boldsymbol{K} & 0 \end{array}\right]\left[\begin{array}{cc} \boldsymbol{R} & \boldsymbol{T} \\ 0 & 1 \end{array}\right] X=\boldsymbol{M} X, \end{aligned} $ | (1) |
其中,(u,υ)为像点在图像像素坐标系中的坐标;(Xw, Yw, Zw)为目标点在世界坐标系中的坐标;K为摄像机的内参矩阵,由f/dx,f/dy,u和υ组成,由摄像机自身决定;R为世界坐标系与摄像机坐标系之间的旋转矩阵;T为世界坐标系与摄像机坐标系之间的平移矩阵。R和T称为摄像机的外参矩阵。若要求得目标点在三维空间的准确位置,就必须求得摄像机的内参矩阵和外参矩阵,这个过程称为摄像机的标定。
若摄像机标定已完成,且像点P1和P2的像素坐标均已获取,那么由(1)式可得
| $ z_{1}\left[\begin{array}{l} u_{1} \\ v_{1} \\ 1 \end{array}\right]=\boldsymbol{M}_{1}\left[\begin{array}{l} x_{\mathrm{w}} \\ y_{\mathrm{w}} \\ z_{\mathrm{w}} \\ 1 \end{array}\right]=\left[\begin{array}{llll} m_{111} & m_{121} & m_{131} & m_{141} \\ m_{211} & m_{221} & m_{231} & m_{241} \\ m_{311} & m_{321} & m_{331} & m_{341} \end{array}\right]\left[\begin{array}{l} x_{\mathrm{w}} \\ y_{\mathrm{w}} \\ z_{\mathrm{w}} \\ 1 \end{array}\right], $ | (2) |
| $ z_{2}\left[\begin{array}{l} u_{2} \\ v_{2} \\ 1 \end{array}\right]=\boldsymbol{M}_{2}\left[\begin{array}{l} x_{\mathrm{w}} \\ y_{\mathrm{w}} \\ z_{\mathrm{w}} \\ 1 \end{array}\right]=\left[\begin{array}{llll} m_{112} & m_{122} & m_{132} & m_{142} \\ m_{212} & m_{222} & m_{232} & m_{242} \\ m_{312} & m_{322} & m_{332} & m_{342} \end{array}\right]\left[\begin{array}{l} x_{\mathrm{w}} \\ y_{\mathrm{w}} \\ z_{\mathrm{w}} \\ 1 \end{array}\right], $ | (3) |
其中,(u1, υ1, 1)和(u2, υ2, 1)为像点P1和P2的齐次像素坐标,(xw, yw, zw, 1)为目标点P的齐次世界坐标。对(2)式、(3)式进行拆分并消去未知数z1和z2,可以得到关于xw,yw,zw的4个线性方程组成的方程组
| $ \left\{\begin{array}{l} \left(u_{1} m_{311}-m_{111}\right) x_{\mathrm{w}}+\left(u_{1} m_{321}-m_{121}\right) y_{\mathrm{w}}+\left(u_{1} m_{331}-m_{131}\right) z_{\mathrm{w}}=m_{141}-u_{1} m_{341} \\ \left(v_{1} m_{311}-m_{211}\right) x_{\mathrm{w}}+\left(v_{1} m_{321}-m_{221}\right) y_{\mathrm{w}}+\left(v_{1} m_{331}-m_{231}\right) z_{\mathrm{w}}=m_{241}-v_{1} m_{341} \\ \left(u_{2} m_{312}-m_{112}\right) x_{\mathrm{w}}+\left(u_{2} m_{322}-m_{122}\right) y_{\mathrm{w}}+\left(u_{2} m_{332}-m_{132}\right) z_{\mathrm{w}}=m_{142}-u_{2} m_{342} \\ \left(v_{2} m_{312}-m_{212}\right) x_{\mathrm{w}}+\left(v_{2} m_{322}-m_{222}\right) y_{\mathrm{w}}+\left(v_{2} m_{332}-m_{232}\right) z_{\mathrm{w}}=m_{242}-v_{2} m_{342} \end{array}\right., $ | (4) |
对(4)式采用最小二乘法求解可以求得目标点在空间的准确三维坐标[11]。
2 实验及图像处理测量系统如图 3,由一台高速相机、两个平面镜、一个棋盘格标定板、高精度四维平台和一台电脑组成。通过电脑控制平台在x,y和z方向移动,高速相机对被测物运动图像进行采集并通过数据线传输到电脑,由电脑对图像进行处理。实验获取图片如图 4。

|
| 图 3 测量系统 Fig. 3 The measuring system |

|
| 图 4 实验获取图片 Fig. 4 The pictures obtained from the experiment |
在获取实验图像后,我们对图像进行分割,分别得到左右虚拟相机的图像,并采用张正友标定法对摄像机进行标定,标定结果为
| $ \boldsymbol{K}_{1}=\left[\begin{array}{ccc} 8\;355.823\;14 & 0 & 0 \\ 0 & 8\;436.688\;18 & 0 \\ -74.281\;31 & 373.970\;25 & 1 \end{array}\right] \text {, } $ | (5) |
| $ \boldsymbol{K}_{\mathrm{r}}=\left[\begin{array}{ccc} 8\;478.417\;34 & 0 & 0 \\ 0 & 8\;482.765\;71 & 0 \\ 479.500\;00 & 539.500\;00 & 1 \end{array}\right], $ | (6) |
| $ \boldsymbol{R}=\left[\begin{array}{rrr} 0.990\;01 & -0.033\;07 & 0.137\;05 \\ 0.034\;79 & 0.999\;34 & -0.010\;19 \\ -0.136\;62 & 0.014\;86 & 0.990\;51 \end{array}\right], $ | (7) |
| $ \boldsymbol{T}=\left[\begin{array}{llll} -225.667\;90 & -8.686\;07 & 12.214\;99 \end{array}\right] . $ | (8) |
经过标定得到摄像机的内外参数,可以对目标物体进行测试。在拍摄过程中受设备自身以及拍摄环境中噪声、光照等因素的影响,图像质量下降。故在得到图像之后,需要对图像进行一系列处理,提高图像的质量,尽可能地接近目标物体的真实情况。
以其中一幅图像为例,如图 5(a)为虚拟相机得到的图像。首先,通过摄像机的标定参数,对图像进行畸变修正,并且对修正过的图像进行掩膜处理,保留特征点的像素信息,将特征点以外的像素值设置为0。这个过程称为图像的预处理,处理后的图像如图 5(b)。接下来对图像进行滤波,通过滤波去除由于拍摄环境中光线对图像造成的影响(主要是椒盐噪声和高斯噪声),高斯滤波能够在很大程度上保留图像的边缘信息[11],滤波后的图像如图 5(c)。对于滤波后的图像进行边缘检测,提取像素值发生突变的位置,所构成的曲线即特征点的边缘,边缘检测结果如图 5(d)。

|
| 图 5 图像处理。(a)初始图像;(b)图像处理;(c)图像滤波;(d)边缘检测 Fig. 5 The image processing. (a) The original image; (b) image preprocessing; (c) image filtering; (d) edge detection |
经过一系列处理后的图像,对其特征点中心坐标进行提取,并以左虚拟相机的摄像机坐标系为世界坐标,由(4)式可得特征点在空间的三维坐标。
模拟实验分为两组进行,第1组模拟实验两平面镜距离被测物0.5 m左右,第2组模拟实验两平面镜距离被测物2 m左右。
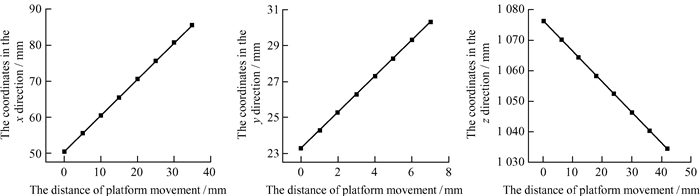
在第1组模拟实验中,x方向的步长为5 mm,y方向的步长为1 mm,z方向的步长为6 mm,特征点在空间三维位置坐标重构结果如表 1。由三维坐标绘制x,y和z方向的运动图像如图 6。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| x | 50.437 | 55.477 | 60.525 | 65.570 | 70.609 | 75.638 | 80.669 | 85.621 |
| y | 23.282 | 24.285 | 25.289 | 26.291 | 27.298 | 28.303 | 29.309 | 30.314 |
| z | 1 076.258 | 1 070.216 | 1 064.247 | 1 058.299 | 1 052.358 | 1 046.386 | 1 040.359 | 1 034.395 |
|
| 图 6 坐标变化图 Fig. 6 The coordinate change diagram |
已知平台在x,y和z方向的移动步长,通过相邻两点坐标之差可以求出计算结果与实际运动距离之间的误差,计算结果与实际运动距离之间的误差如表 2。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| x/% | 0.8 | 0.96 | 0.9 | 0.6 | 0.58 | 0.62 | 0.96 |
| y/% | 0.3 | 0.4 | 0.2 | 0.7 | 0.5 | 0.6 | 0.5 |
| z/% | 0.7 | 0.51 | 0.86 | 0.98 | 0.46 | 0.45 | 0.6 |
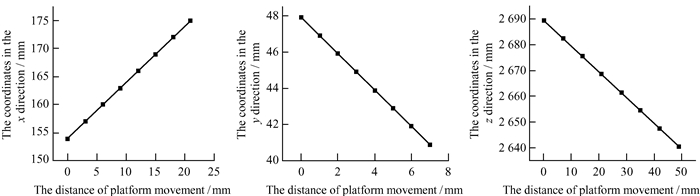
为了排除数据的偶然性,在第2组实验过程中选择不同步长进行测量,x方向的步长为3 mm,y方向的步长为1 mm,z方向的步长为7 mm,特征点在空间三维位置坐标重构结果如表 3。由三维坐标绘制x,y和z方向运动图像如图 7。本组模拟实验计算结果与实际运动距离之间的误差如表 4。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| x | 153.921 | 156.943 | 159.968 | 162.986 | 166.009 | 169.022 | 172.048 | 175.065 |
| y | 47.927 | 46.920 | 45.915 | 44.911 | 43.902 | 42.899 | 41.893 | 40.883 |
| z | 2 689.469 | 2 682.529 | 2 675.566 | 2 668.563 | 2 661.520 | 2 654.457 | 2 647.436 | 2 640.378 |
|
| 图 7 坐标变化图 Fig. 7 The coordinate change diagram |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| x/% | 0.73 | 0.83 | 0.59 | 1.0 | 0.43 | 0.84 | 0.59 |
| y/% | 0.7 | 0.49 | 0.48 | 0.86 | 0.24 | 0.62 | 0.99 |
| z/% | 0.85 | 0.53 | 0.04 | 0.61 | 0.89 | 0.29 | 0.83 |
由图 6和图 7可以看出,计算的x,y和z方向的坐标变化与实验平台在三维方向的运动有良好的线性关系。通过计算结果与实际运动距离之间的误差可以看出,相邻两点间的距离与实际平台运动距离之间的误差均小于1%,能够较好地符合真实情况。当两平面镜与被测物距离为0.5 m时的误差与两平面镜与被测物距离为2 m时的误差均小于1%,证明该算法有较高的稳定性。
3 虚拟双目视觉与真实双目视觉的比较为评价虚拟双目视觉精度与真实双目视觉精度的差距,评估虚拟双目视觉的可行性,我们采用真实双目视觉对被测物三维位置进行测量。两相机与被测物距离2 m左右,实验平台在x,y和z方向分别以步长5 mm,1 mm,6 mm移动,通过对图像的处理与一系列计算,得到被测物在空间的三维位置如表 5。真实双目视觉计算结果与实际运动距离之间的误差如表 6。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| x | 10.728 | 15.753 | 20.777 | 25.800 | 30.820 | 35.841 | 40.863 | 45.882 |
| y | 32.112 | 33.117 | 34.122 | 35.126 | 36.131 | 37.135 | 38.139 | 39.143 |
| z | 2 044.055 | 2 050.086 | 2 056.115 | 2 062.145 | 2 068.172 | 2 074.197 | 2 080.221 | 2 086.244 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| x/% | 0.50 | 0.48 | 0.46 | 0.40 | 0.42 | 0.44 | 0.38 |
| y/% | 0.51 | 0.49 | 0.45 | 0.47 | 0.44 | 0.43 | 0.37 |
| z/% | 0.51 | 0.48 | 0.50 | 0.45 | 0.41 | 0.40 | 0.38 |
对比虚拟双目视觉计算误差与真实双目视觉计算误差,两者均小于1%,虚拟双目视觉与真实双目视觉之间的误差仅为0.3%左右,说明虚拟双目视觉能够较好地达到真实双目视觉的精度,同时说明该方法具有较高的可行性。
4 结论本文通过对虚拟双目视觉原理及构成系统的研究,通过高速相机与平面镜组成的虚拟双目视觉系统对天线副面随俯仰角在空间的位置变化进行模拟实验,重建了被测物随实验平台移动在三维方向的运动情况,结果能够较好地符合真实情况。同时对虚拟双目视觉与真实双目视觉的对比表明,该方法具有较高的可行性,为快速重建和修正天线副面位置提供了一种有效的方法。
5 应用设想本文方法针对大口径射电望远镜因不同工况导致副面位置的变化,进而造成天线指向精度及效率下降的问题,通过对副面位姿的实时测量为后续的修正提供重要支持。该测量系统将靶标固定于天线副面上,两平面镜固定于天线主面,高速相机固定于天线副面撑腿位置,调试两平面镜之间夹角以及镜面与高速相机的相对位置,保证靶标能够在两镜面内完全呈现,同时保证高速相机能够对两平面镜中的成像情况进行记录。通过实验验证测量精度达到0.01 mm量级,由于系统简易,数据处理方法成熟,系统长期工作可靠性高,能够满足天线整体技术要求。
| [1] |
魏善祥, 王启明, 孔德庆, 等. 大型双反射面天线指向误差评估算法[J]. 天文研究与技术, 2020, 17(4): 513–521 WEI S X, WANG Q M, KONG D Q, et al. Algorithm for estimating pointing error of large dual-reflector antenna[J]. Astronomical Research & Technology, 2020, 17(4): 513–521. DOI: 10.3969/j.issn.1672-7673.2020.04.012 |
| [2] |
王锦清, 虞林峰, 赵融冰, 等. 大型射电望远镜高精度指向偏差检测方法[J]. 中国科学: 物理学力学天文学, 2017, 47(12): 125–134 WANG J Q, YU L F, ZHAO R B, et al. High precision pointing error detection method for large radio telescope[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2017, 47(12): 125–134. |
| [3] |
王锦清, 赵融冰, 虞林峰, 等. 基于干涉全息法测量射电望远镜主面重力变形和副面位姿[J]. 中国科学: 物理学力学天文学, 2019, 49(10): 135–144 WANG J Q, ZHAO R B, YU L F, et al. Main reflector gravity deformation and sub-reflector position measurement for radio telescope based on interferometer[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2019, 49(10): 135–144. |
| [4] |
许谦, 王从思, 易乐天. 基于应变的变形副反射面位姿形貌快速重构方法[J]. 天文学报, 2020, 61(5): 46–53 XU Q, WANG C S, YI L T. Rapid reconfiguration method for deformed subrefector position attitude and shape based on strain[J]. Acta Astronomica Sinica, 2020, 61(5): 46–53. |
| [5] | SÜSS M, KOCH D, PALUSZEK H. The Sardinia Radio Telescope (SRT) optical alignment[C]// Proceedings of SPIE. 2012. |
| [6] | PISANU T, BUFFA F, CONCU R, et al. A PSD (position sensing device) to map the shift and tilt of the SRT secondary mirror[C]// Proceedings of SPIE. 2014. |
| [7] |
江永琛, 王锦清, 苟伟, 等. PSD法测量大型射电望远镜副面位姿[J]. 天文学报, 2019, 60(6): 98–107 JIANG Y C, WANG J Q, GOU W, et al. The measurement of sub-reflector's displacements of large radio telescopes by PSD method[J]. Acta Astronomica Sinica, 2019, 60(6): 98–107. |
| [8] |
侯雨雷, 段艳宾, 窦玉超, 等. 65 m射电望远镜天线副面调整机构标定研究[J]. 中国机械工程, 2013, 24(24): 3318–3322, 3328 HOU Y L, DUAN Y B, DOU Y C, et al. Calibration of adjusting mechanis for subreflector of a 65 meters radio telescope[J]. China Mechanical Engineering, 2013, 24(24): 3318–3322, 3328. DOI: 10.3969/j.issn.1004-132X.2013.24.011 |
| [9] |
尹航, 陈卯蒸, 刘志勇. 基于惯性测量的天线副面位姿测量系统的设计[J]. 天文研究与技术, 2018, 15(4): 390–396 YIN H, CHEN M Z, LIU Z Y. The position and posture of deputy reflection surface measurement system design based on inertial measurement technology[J]. Astronomical Research & Technology, 2018, 15(4): 390–396. DOI: 10.3969/j.issn.1672-7673.2018.04.003 |
| [10] |
孙瑞轩, 董浩, 肖磊, 等. 基于双目立体视觉技术的运动物体空间位置信息测量方法研究[J]. 河北工业科技, 2017, 34(1): 30–35 SUN R X, DONG H, XIAO L, et al. Rescarch on measurement method of spatial position information of moving objects based on binocular stereo vision technology[J]. Hebei Journal of Industrial Science and Technology, 2017, 34(1): 30–35. |
| [11] |
林碧华, 张开淋, 刘向军. 基于虚拟双目视觉的电器电弧弧根三维运动特性的研究方法[J]. 电器与能效管理技术, 2017(23): 1–5, 22 LIN B H, ZHANG K L, LIU X J. Research method for three-dimensional electric arc root movemen characteristics based on virtual binocular vision[J]. Electrical & Energy Management Technology, 2017(23): 1–5, 22. |



