2. 中国科学院云南天文台,云南 昆明 650216;
3. 云南省计算机应用技术重点实验室,云南 昆明 650500
2. Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, China;
3. Key Laboratory of Applications of Computer Technology of Yunnan Province, Kunming 650500, China
为了减少电磁干扰对天文观测的影响,射电望远镜台站一般选择在高海拔、人迹稀少的地区,但这也限制了人工现场干预观测的能力。当前望远镜正朝着巨型化、复杂化发展,望远镜的正常运转需要多种组件协同工作[1],依赖操作人员手工控制已变得越来越困难。因此,自主观测是望远镜观测控制系统的共同需求。自主观测是指根据观测计划自动进行调度的观测模式,而观测计划的编排是望远镜实现自动化观测控制的前提。
目前观测计划的编排主要集中于长期观测申请调度,通常是望远镜科学委员会根据科学目标、不同的观测申请赋予不同的科学价值权重后,通过优化方法给出长期的计划编排[2]。而对于40 m射电望远镜,一个重要需求是给出一系列观测目标,使望远镜尽可能在短时间内完成所有目标的观测任务,通常是一天内完成几十颗射电源的短期观测编排。显然,目前其他望远镜系统的长期观测编排方法不能满足40 m射电望远镜短期编排的需求。
不同于长期观测编排,短期编排需要给出目标具体的开始和结束观测时间,而时间变量是连续的,因此短期编排属于连续最优化问题。观测目标的位置随时间不停变化,不同的观测目标一天内在望远镜视场中出现的时间有限,同时还需要考虑从一个观测目标转动到另一个目标的过程中,由于望远镜本身的机械问题,可能出现限位,以及望远镜不同观测方向对观测数据质量的影响,这些都是短期编排区别于长期编排的地方,也是优化的难点。本文首先回顾当前主要的观测编排方法;接着介绍将望远镜观测源的编排转换成混合整数线性规划问题中的决策变量、目标函数和约束条件的定义,给出了该方法在40 m射电望远镜上的测试结果;最后总结并讨论了40 m射电望远镜观测编排未来的研究工作。
1 相关工作调度问题已在电力、运输、航空、计算机以及工业生产等领域得到了广泛的研究,望远镜观测目标的编排是该问题在天文领域的实际应用。哈勃空间望远镜的Spike系统自1990年投入使用,系统的核心算法为迭代修正搜索算法[3]。迭代修正搜索算法的核心思路是将望远镜时间分配问题抽象为一个约束优化问题,通过3步进行求解:(1)通过某种启发式算法构造初始解,该初始解可以违反约束条件,根据具体需求选择启发式算法,但启发式过程均基于对约束程度的量化并且选择容易计算的量化方式;(2)利用启发式的修正算法减少约束的违反条件;(3)通过从时间分配表中去除存在冲突的活动来消除冲突[4]。
绿岸射电望远镜(Green Bank Telescope, GBT)采用一个自动动态调度系统[5],核心思想是基于一种排序的算法确定观测计划之间的优先次序。文[5]描述了绿岸射电望远镜使用的包括预报天气条件、观测效率、目标坐标等变量的排序算法,以及调度观测中使用的一些特定变量。
撒丁岛射电望远镜(Sardinia Radio Telescope, SRT)[6]参考绿岸射电望远镜的动态调度系统,考虑长期和短期编排问题,在模拟结果中,以48 h为周期,1 h作为一个时间槽。每个观测计划赋予一个科学价值,占用2~6 h,使用模拟退火算法优化观测编排,加入水汽和天气等限制条件。
500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope, FAST)[7]以最小化寻址代价和最大化科学价值为目标函数,限制条件考虑源的可见性、射频干扰等因素,同时使用边缘检测方式减小问题空间,加快优化速度。望远镜使用中国虚拟天文台在线观测提案系统,本质上还是中长期的观测编排。
其他望远镜系统的观测编排也大多是观测提案的编排,比如基于进化算法的低频阵列(Low Frequency Array, LOFAR)观测调度[8],基于模拟退火和动态规划实现的阿塔卡马大型毫米波/亚毫米波阵列(Atacama Large Millimeter/submillimeter Array, ALMA)观测调度[9]。40 m射电望远镜作为单碟射电望远镜,在短期的观测编排中,需要在更短的时间槽内,按目标源进行分配,而不是按观测提案进行分配。现有的中长期观测提案的编排方法,显然无法解决按目标源进行观测时间分配的需求。
2 模型设计 2.1 问题描述40 m射电望远镜短期观测目标编排需求通常是在一天(或几个小时)内给定一系列观测目标信息,包含观测目标的名称(J2000纪元)、位置和所需观测时长,如表 1。
| Name of observation source | RA | DEC | Observation time /min |
| 0034-0721 | 00 34 08.8703 | -07 21 53.409 | 48 |
| 0139+5814 | 01 39 19.7401 | +58 14 31.819 | 48 |
| 1559-4438 | 15 59 41.5261 | -44 38 45.9018 | 24 |
| 1745-2900 | 17 45 40.190005 | -29 00 30.37032 | 48 |
短期编排的结果是得出每个目标开始和结束的观测时间,并最大化望远镜的利用率。同时需要考虑:
(1) 所有观测目标安排观测。每颗目标源的观测时长要求集中在24~48 min,保证编排时间满足观测时长要求。
(2) 分配时间粒度。时间分配粒度太大,造成时间片的浪费;时间分配粒度太小,造成参数空间膨胀,直接影响最优化求解的性能。
(3) 望远镜硬件的限位条件。在观测过程中,源的位置不断变化,而望远镜只能在一定范围内转动,因此须满足在源的编排时间内,望远镜可以转动到目标源,即满足望远镜硬件的限位条件。
(4) 最优观测时间。根据40 m射电望远镜的观测经验,天线俯仰角在40~60°内观测比较好,这时增益较大,且增益变化不大,观测源受地面噪声影响相对较小,观测获取的数据质量更好。因此编排时,优先考虑这个位置范围内的源,源的位置高度可用Airmass衡量,Airmass值近似等于1/sinα,其中α为源的高度角。图 1显示了2020年12月21日,源2055+3630,0837-4135和0358+5413的Airmass随时间变化的曲线。

|
| 图 1 源2055+3630, 0837-4135和0358+5413在2020年12月21日不同时刻的Airmass值 Fig. 1 The Airmass of 2055+3630, 0837-4135, 0358+5413 at different times on Dec. 21, 2020 |
根据40 m射电望远镜短期观测目标编排的需求和限制条件,我们假设总共有K个观测目标,一个观测目标在观测过程中需要考虑观测时长以及望远镜从第1颗源的跟踪状态切换到第2颗源的跟踪状态消耗的时间。因此,一个观测目标t占用的时间窗为转向时间Ts+观测时间To,可以表示为
| $ T_{t}^{i}=T_{\mathrm{s}}^{i-1 \rightarrow i}+T_{\mathrm{o}}, $ | (1) |
其中,转向时间依赖上一个观测目标结束时望远镜的位置(方位、俯仰角度)。如果是首个观测目标,则转向时长根据望远镜初始方位角和高度角进行计算。
2.2 决策变量在望远镜短期观测编排中,时间是最主要的变量,时间直接决定了源的位置,也间接影响源的观测时长。在40 m射电望远镜的短期目标编排中,目标源观测时长的单位是min,我们将时间的分配粒度设置为min,整个观测计划的总时间M为24 × 60 × d min,其中,d为编排计划的天数。
首先对于每个观测目标{Tj, j∈K},定义目标Tj的开始观测时间为tjs∈[0, M],结束观测时间为tje∈[0, M],在优化过程中,为加快求解速度,tjs和tje范围取目标Tj第1个可用时间槽的开始时间和最后一个可用时间槽的结束时间。我们取Airmass的范围为[2, 10],可计算获得每个观测目标在观测总时间内的s个可观测的时间槽,如图 2,每个观测源在一天内通常有1~4个可观测的时间槽,单个目标在所有可观测时间槽的Airmass均在[2, 10]。定义二进制变量

|
| 图 2 源0922+0638和1136+1551在2020年12月21日的可用时间槽 Fig. 2 The available time slots of 0922+0638 and 1136+1551 on Dec. 21, 2020 |
观测目标编排重要的一点是编排源的观测顺序,定义二进制变量
| $ d_{i j}=\arccos \left[\sin \delta_{1} \sin \delta_{2}+\cos \delta_{1} \cos \delta_{2} \cos \left(\alpha_{1}-\alpha_{2}\right)\right]. $ | (2) |
根据40 m射电望远镜的经验值,最大的源目标切换时间约为6 min,这里源切换时间矩阵近似为
| $ \boldsymbol{S} \approx 6 \boldsymbol{\widetilde{D}}, $ | (3) |
其中,
基于最大化望远镜的利用率、减少源切换时间的原则,目标函数定义为
| $ \min \sum\limits_{i \in J} \sum\limits_{j \in J} y_{i j}\left(t_{j}^{\mathrm{s}}-t_{i}^{\mathrm{e}}\right)+y_{i j} S_{i j} . $ | (4) |
根据40 m射电望远镜短期观测目标编排的问题描述,在最优化目标函数的过程中需要满足以下约束:
(1) 满足每个目标的观测时长要求,即满足结束调度时间减去开始调度时间大于等于观测时长Pj,用公式表示为
| $ t_{j}^{\mathrm{e}}-t_{j}^{\mathrm{s}} \geqslant P_{j}. $ | (5) |
(2) 每个目标有不止一个可观测时间槽,需要保证开始时间和结束时间在同一个时间槽内,如图 3。观测源0922+0638出现的编排1并不满足(2),结束时间未在时间槽内;编排2满足(2),开始时间和结束时间在同一个时间槽内。即如果目标Tj的开始观测时间tjs大于等于一个时间槽的开始时间,则结束时间tje应小于等于这个时间槽的结束时间,用公式表示为
| $ t_{j}^{\mathrm{s}} \geqslant \sum\limits_{n=0}^{N} l_{j, n} L_{j}^{n_{\mathrm{s}}}, t_{j}^{\mathrm{e}} \leqslant \sum\limits_{n=0}^{N} l_{j, n} L_{j}^{n_{\mathrm{e}}}, $ | (6) |

|
| 图 3 第2个约束条件限制示意图 Fig. 3 The diagram of condition restriction under the second constraint |
其中,N为目标Tj的可观测时间槽的数量;Ljns为第n个时间槽的开始时间;Ljne为第n个时间槽的结束时间;
(3) 保证每个目标观测开始时间和结束时间没有相互重叠,即
| $ \text { if } y_{i j}=1 \rightarrow t_{j}^{\mathrm{s}} \geqslant t_{i}^{\mathrm{e}}+S_{i j} . $ | (7) |
如果yij=1,表示完成源Ti的观测后转动到源Tj,需要满足源Tj的开始时间大于等于源Ti的结束时间加上源Ti到源Tj的转换时间Sij。
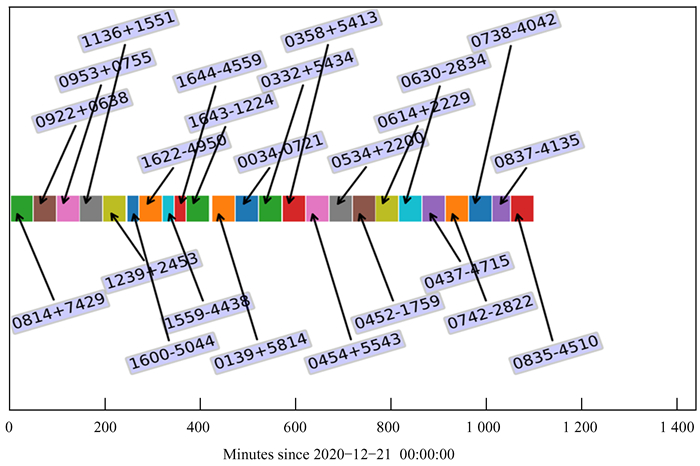
3 实验本文的实验数据来自40 m射电望远镜的真实观测源,短期编排的时间区间为1天,共有24颗观测源,每颗源所需观测时长为24~48 min。实验的硬件环境为1台配置为Intel Xeon CPU E5-2660 v4 CPU@3.4 GHz处理器(56核),512 GB RAM的高性能服务器,求解器使用Gurobi 9.1。以2020年12年21日为例,如图 4,24颗目标源全部编排,并不存在时间交叉的情况,经过验证都在可观测的时间槽内。
|
| 图 4 24颗观测源在2020年12月21日的观测时间分配 Fig. 4 The observation time scheduling results of the 24 sources on Dec. 21, 2020 |
Gap即百分比界差,是求解大规模混合整数规划问题时非常重要的参数,可视为在去除问题参数整数取值的限制后,问题松弛解与最优解之间的绝对差距,
| $ G a p=\left|\frac{O P T-L P}{L P}\right|. $ | (8) |
其中,OPT为当前最优解;LP为去掉整数约束后的松弛最优解。实验使用56个线程,模型可在300 s内将Gap控制在0.1以下。
4 总结本文利用线性规划方法对40 m射电望远镜的短期观测目标编排问题进行了建模,详述了在短期观测编排过程中遇到的限制条件,利用非线性混合整形线性规划解决了这一约束优化问题。实验结果证明方法的可用性。
短期观测目标编排问题中,机会源临时插入观测,整个观测计划就需要重新编排,因此求解速度是短期观测目标编排的重要考量。未来我们研究使用其他的优化算法进一步提高编排性能,减少望远镜等待编排的时间,同时考虑加入目标源的权重,在望远镜空闲时间对权重高的目标多次观测。此外,利用已观测的脉冲星数据反演天线干扰情况与方位和俯仰之间的关系图,在编排目标源时优先安排干扰较小的源。在目前的模型中,源切换的时间使用球面距离近似估计,不完全准确,未来我们研究如何在优化过程中根据源的方位角和高度角以及望远镜的实时指向位置动态计算源的切换时间。
| [1] |
邓辉, 钟文杰, 付映雪, 等. 基于ZeroMQ的新一代望远镜自动控制系统的通信框架设计[J]. 天文研究与技术, 2018, 15(3): 308–314 DENG H, ZHONG W J, FU Y X, et al. The design of communication framework for a new generation of telescope autonomous control system based on ZeroMQ[J]. Astronomical Research & Technology, 2018, 15(3): 308–314. |
| [2] |
李曼迪, 葛亮, 姜晓军. 望远镜观测调度系统研究进展[J]. 天文学进展, 2019, 37(4): 455–468 LI M D, GE L, JIANG X J. Research progress on observation scheduling system of telescope[J]. Progress in Astronomy, 2019, 37(4): 455–468. |
| [3] | SPONSLER J, JOHNSTON M, MILLER G, et al. An AI scheduling environment for the Hubble Space Telescope[C]// Proceedings of the 8th Computing in Aerospace Conference. 1991. |
| [4] | 刘琪. 丽江2.4米光学望远镜观测时间自动分配算法研究[D]. 天津: 天津大学, 2016. LIU Q. Automatic time allocation for Lijiang 2.4 m optical telescope[D]. Tianjin: Tianjin University, 2016. |
| [5] | BALSER D S, BIGNELL C, BRAATZ J, et al. Gbt dynamic scheduling system: algorithms, metrics, and simulations[C]// Proceedings of the Astronomical Data Analysis Software and Systems XVⅢ. 2009. |
| [6] | NASIR F T, CASTIGLIA C, BUFFA F, et al. Weather forecasting and dynamic scheduling for a modern cm/mm wave radiotelescope[J]. Experimental Astronomy, 2013, 36(1): 407–424. DOI: 10.1007/s10686-013-9339-0 |
| [7] | LUO Q, ZHAO L, YU C, et al. Cost-efficient scheduling of FAST observations[J]. Experimental Astronomy, 2018, 45(1): 107–126. DOI: 10.1007/s10686-018-9577-2 |
| [8] | GRIM R, JANSEN M, BAAN A, et al. Use of evolutionary algorithms for telescope scheduling[C]// Proceedings of SPIE. 2002: 51-61. |
| [9] | CLARKE D, AVARIAS J. ALMA scheduling: it's dynamic![C]// Proceedings of the Astronomical Data Analysis Software and Systems XXI. 2012: 177. |
| [10] |
樊东卫, 何勃亮, 李长华, 等. 球面距离计算方法及精度比较[J]. 天文研究与技术, 2019, 16(1): 69–76 FAN D W, HE B L, LI C H, et al. Research on spherical distance computation and accuracy comparison[J]. Astronomical Research & Technology, 2019, 16(1): 69–76. |



