2. 中国科学院大学,北京 100049;
3. 中国科学院月球与深空探测重点实验室,北京 100101;
4. 清华大学工程物理系,北京 100084
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Lunar and Deep-Space Exploration, Chinese Academy of Sciences, Beijing 100101, China;
4. Department of Engineering Physics, Tsinghua University, Beijing 100084, China
嫦娥四号低频射电频谱仪放置在月球背面,由于月球屏蔽了大量来自地球的无线电干扰,因此具有得天独厚的观测条件,可以对太阳等宇宙天体的射电信号进行观测[1]。但是,由于着陆器平台干扰信号比接收的低频射电天文信号大很多,如果不分离平台干扰信号,将无法得到有效的低频射电天文信号数据。因此,本文提出一种有效分离平台干扰信号的算法,实现对干扰的抑制。
在射电天文领域,传统抑制干扰的方法有很多,包括对空白脉冲干扰的时间限制[2],自适应频率选择滤波[3],参数信号相减[4],自适应波束成形[5],时间自适应滤波[6],带有参考天线的频域后相关处理[7],子空间投影的空间滤波[8]等等。截至目前,应用比较广泛的是单通道总功率变化检测器。文[9]基于对功率变化的检测,在RATAN600上实现了改进的功率检测器。文[10]提出在所有滞后的情形下使用量化相关性来测试干扰的存在。文[11]提出了一种基于小波分解的检测器。这些都是单通道检测器,它们不利于干扰的空间特性分析。文[12]提出了结合使用多个望远镜以改善探测质量的方法,此方法用于低频干涉测量,文中还提出了一种基于交叉频谱时间行为的鲁棒数据检测方法。文[6]考虑自适应过滤技术,提出使用参考天线和最小均方(Least Mean Square, LMS)类型算法,消除绿岸望远镜(Green Bank Telescope, GBT)的干扰[6]。文[13]提出一种针对韦斯特博克综合射电望远镜的射电干扰消除子系统。这些都是在射电干扰消除方面典型的例子。
射电干扰信号消除算法主要分为3类:(1)通过线性方式区分射电干扰信号的特点,比如奇异值分解(Singular Value Decomposition, SVD)[14]、主成分分析(Principal Component Analysis, PCA)[15]等等。如果射电干扰在时间和频率上表现出重复模式,这些方法效果很好,但无法处理更多随机信号,例如由卫星引起的不规则信号。(2)基于阈值的算法,例如CUMSUM[8]和SUMTHRESHOLD[4],这些算法简单且可靠有效。(3)使用传统的监督机器学习技术(例如K最近邻和高斯混合模型)对射电干扰信号进行聚类[16]。
嫦娥四号低频射电频谱仪接收的平台干扰信号很强,和太阳爆发峰值的量级10-15W/(m2·Hz)相当,比普通的太阳爆发信号10-18W/(m2·Hz)大3个量级,比太阳宁静时的信号10-22W/(m2·Hz)大7个量级。之前仪器设计时推荐使用的谱减法[17],虽然可以将信号的信噪比提高约30 dB,但是仍然不足以探测有效的射电天文信号。为此,本文提出了基于CLEAN算法的平台干扰信号分离方法,利用低频射电频谱仪3个天线同时观测的信号有相关性的特点,并结合天线之间数据的互相关功率谱、傅里叶级数等工具,有效地分离平台干扰信号,从而实现对干扰的抑制。
1 低频射电频谱仪的工作原理及接收信号的构成 1.1 低频射电频谱仪简介宇宙中的来波信号是一个矢量信号。根据矢量场理论,来波信号可以分解为任意3个互相垂直的分量,只要将这3个分量接收并合成,就可以得到矢量的大小和方向。通过后期处理,我们可以获得电场的频谱和时变信息。
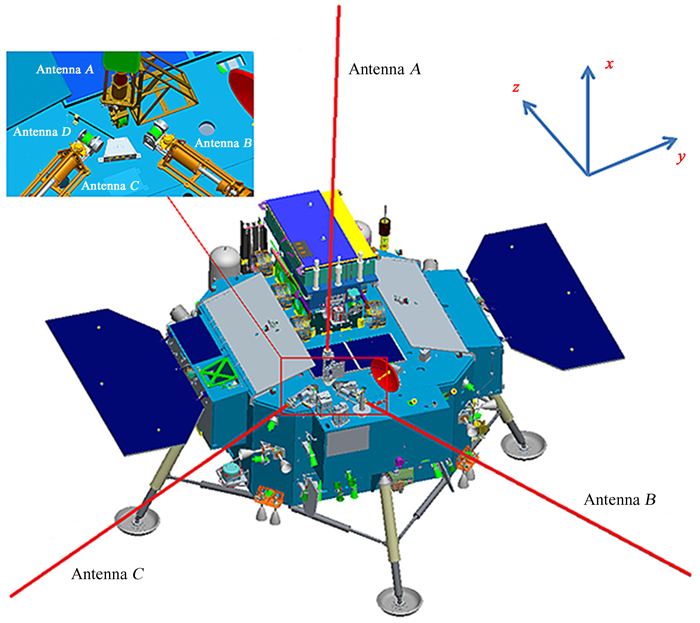
低频射电频谱仪的天线位置分布如图 1。3个分量有源天线接收宇宙的来波电场。3个天线分别标注为天线A、天线B和天线C,两两正交,还有一个短天线D,主要用于接收平台干扰信号, 为天线数据处理做参考。
|
| 图 1 着陆器低频射电频谱仪的天线位置分布 Fig. 1 Antenna location distribution of lander low-frequency radio spectrometer |
低频射电频谱仪具有高频和低频两个频率接收波段,高频对应的频率范围是1~40 MHz,低频对应的频率范围是0.1~2 MHz。接收机灵敏度为
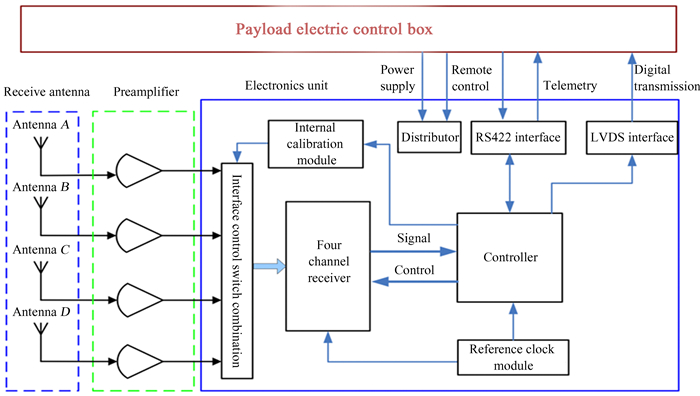
低频射电频谱仪主要由4个接收天线、前置放大器、电子学单元、电缆组件等部分组成。有源天线安装于卫星本体外,其余组件安装于卫星本体内。电子学单元由控制器、配电器、基准时钟模块、四通道接收机、内定标模块、存储单元、通讯接口、数传接口等组成。低频射电频谱仪系统组成及内部各单元与数管分系统、供配电分系统之间的接口关系如图 2。
|
| 图 2 低频射电频谱仪系统组成及接口关系示意图 Fig. 2 Schematic diagram of low-frequency radio spectrometer, with system composition and interface relationship |
低频射电频谱仪有6种工作模式,分别为(1)待机模式;(2)内定标模式;(3)时频对比模式;(4)频谱巡查模式;(5)三天线模式;(6)时域模式。其中应用最广泛的是三天线工作模式,在此模式下,低频射电频谱仪分别采集4个天线4个通道的科学数据。本文对三天线模式下的数据进行处理。
低频射电频谱仪的科学数据分为0A级、0B级、01级、2A级、2B级和2C级共6级。预处理数据经过分路解帧和分包,生成0A级数据产品;0A级数据经过排序、去重复、两站优化拼接、去源包包头,根据采样周期形成低频射电频谱仪数据块,生成0B级数据产品;多个0B级数据文件拼合成一个探测周期,生成01级数据产品;对01级数据进行傅里叶变化、定标等操作,生成2A级数据产品;2A级数据加入太阳位置等信息,生成2B级数据产品;对2B级数据进行消噪声处理,生成2C级数据产品。其中1级数据为时域数据,2级数据为频域数据。本文所用的原始数据均为1级数据。
1.2 接收信号的构成低频射电频谱仪接收的信号主要由3部分构成:(1)平台干扰信号;(2)接收机噪声;(3)低频射电天文信号。
平台干扰信号的特点是幅度相对较强,两天线之间的相关性高。如果干扰源位置确定,各天线接收信号之间的强度比例不随时间变化。来自电子设备的干扰信号,一部分是固定频率的发射信号,如通讯发射机、时钟信号等,另一部分是宽带随机噪声信号,这是由电磁兼容(Electro Magnetic Compatibility, EMC)问题带来的。最终的平台干扰信号既有确定变化的成分,也有宽带随机噪声信号。
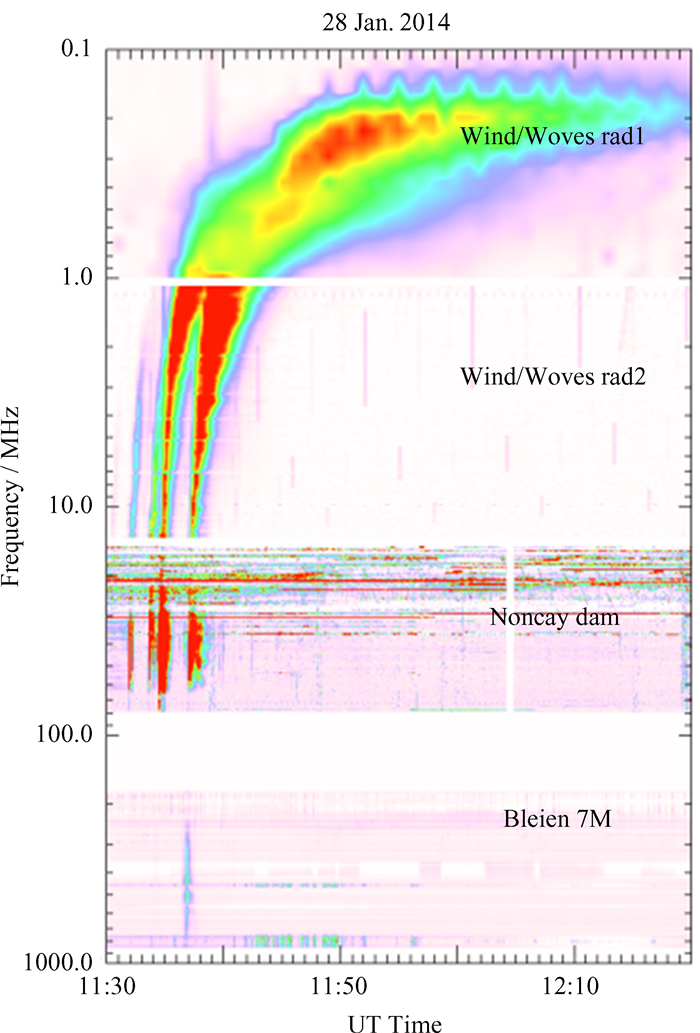
低频射电天文信号具有一定的相关性,除此之外,还有一些天体源特有的性质。比如,低频太阳射电信号有瞬时和频谱漂移等特点,具有很强的频谱可识别特征[18],如图 3。再比如,快速射电暴(Fast Radio Burst, FRB)FRB200428的持续时间约0.61 ms,能量通量(Fluence)达到1.5 MJyms[19],辐射强度足以被低频射电频谱仪探测到。另外,由于仪器指向随月球的自转而改变,低频射电天文信号在低频射电频谱仪各天线之间的强度比例随时间呈现有规律的变化。所有这些特性有助于在强平台干扰的背景下识别有用的低频射电天文信号。
|
| 图 3 低频太阳射电信号频谱 Fig. 3 Low frequency spectrum of solar radio signal |
接收机噪声的特点是天线两两之间无相关性。我们可以利用该特性,通过计算天线之间数据的相关性,评估平台干扰信号的分离程度。
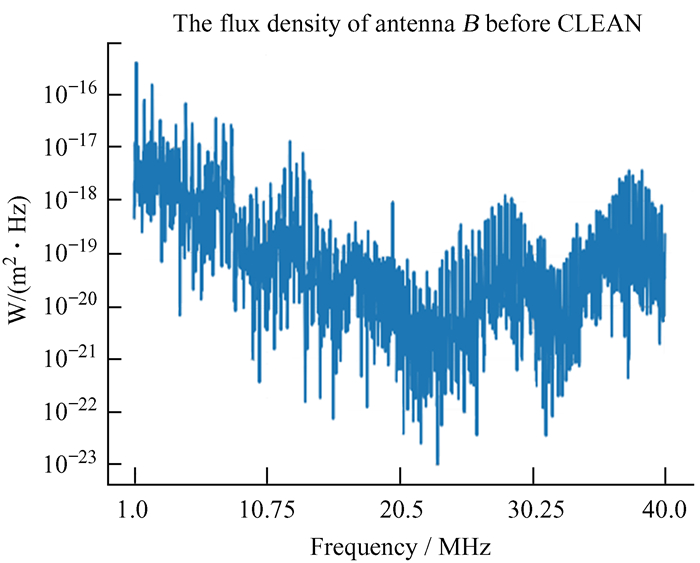
图 4展示了低频射电频谱仪B天线观测的一个频谱实例。由图 4可知,频谱在1 MHz附近的流量密度大约为10-15W/(m2·Hz),与太阳爆发峰值流量密度相当,比太阳爆发流量密度大2~3个量级,说明着陆器平台干扰比我们希望探测的太阳爆发信号大许多。如果不通过一定的方法分离平台干扰信号,将无法有效提取低频射电天文信号。
|
| 图 4 天线B采集的高频波段的一个频谱实例,对应第23月昼第2道数据 Fig. 4 An example of the spectrum of antenna B at the high-frequency band, corresponding to the second channel data on the 23rd moon day |
低频射电源与平台干扰源在低频射电频谱仪的3个天线上激发出互相关联的接收信号。本文的目的是从两组信号的相关性出发,借助CLEAN算法以及互相关功率谱、傅里叶级数等工具,把低频射电频谱仪观测信号中的强相关成分与部分相关成分分离,以便进行后续的科学分析。分离之后,原始的低频射电频谱仪时域信号被切分为两部分,即强相关的CLEAN模型信号和部分相关的残余信号。在这个过程中,原始信号的信息没有丢失或损伤。
CLEAN模型信号主要由平台干扰信号组成。当低频强射电爆发信号到来时,进入CLEAN模型信号。由于数据传输的限制,低频射电频谱仪大约以1 s为间隔采集一道时域数据,采集间隔并不严格相等。每道数据由4 096个数据组成,采样频率为100 MHz,采样持续时间大约40 μs。因此,不同道时域数据之间有明显的差别。
为了寻找有效的低频强射电爆发信号,我们需要提取每道时域数据的CLEAN模型信号,并对其中的确定成分和宽带随机成分进行处理。例如,对于CLEAN模型信号中的确定时域变化结构或频谱成分,我们把它们当作系统误差,借助CLEAN算法扣除,剩下的CLEAN模型信号,由宽带随机信号组成,通过平均多道数据的方式降低涨落水平,提高探测低频强射电天文信号的灵敏度。
残余信号主要由不相关的接收机噪声、未分离的平台干扰信号以及常规低频射电天文信号组成。残余信号的特征类似于随机白噪声,没有确定的信号成分,可以借助数理统计工具进行分析。例如,借鉴微波辐射计的思想,通过积分平均的方式进一步提高残余信号的探测灵敏度。
我们的最终目标是从嫦娥四号低频射电频谱仪的观测数据中搜索低频射电天文信号,并进行深入的科学研究。此时,无论是CLEAN模型信号还是残余信号都缺一不可。
时标短、幅度强的低频强射电爆发往往隐藏在CLEAN模型信号中,对这类射电爆发信号的提取离不开宁静状态的CLEAN模型信号的分类整理。特别强的低频射电天文爆发,在单道数据中有明显异常的表现。此时,可以借助交叉相关直接扣除该道数据对应的宁静状态的CLEAN模型信号,获得射电爆发信号的时域、频谱特征。如果射电爆发强度与平台干扰中的宽带随机成分接近,先扣除CLEAN模型信号中的确定成分,再通过多道数据积分平均的方式提高探测灵敏度,最终获得低频射电天文爆发信号的时域、频谱特征。
一些时标长(超过月量级)、幅度弱的低频射电天文信号隐藏在残余信号中。为了探测这类弱信号,首先借助星载定标装置或其他外部稳定的定标源,确认接收机工作稳定。之后,可以直接从残余信号出发,同样借助微波辐射计的思想,通过积分平均提高残余信号的探测灵敏度。理论上,低频射电频谱仪3个天线残余信号的积分值随月球自转发生调制变化, 这样的调制信息甚至可以用来对全天进行粗略成像。
2.1 CLEAN算法分离平台干扰信号的基本思路设低频射电频谱仪中一个天线接收的信号为S(t),它包含平台干扰信号I(t)、宇宙射电信号C(t)以及接收机噪声N(t)。这些信号之间的关系为
| $ \begin{aligned} &S_{A}(t)=\alpha_{A}(t) I(t)+\beta_{A}(t) C(t)+N_{A}(t), \\ &S_{B}(t)=\alpha_{B}(t) I(t)+\beta_{B}(t) C(t)+N_{B}(t), \\ &S_{C}(t)=\alpha_{C}(t) I(t)+\beta_{C}(t) C(t)+N_{C}(t), \end{aligned} $ | (1) |
其中,SA(t),SB(t)和SC(t)分别为天线A,B和C接收的信号;NA(t),NB(t)和NC(t)分别为天线A,B和C对应接收机的本地噪声,它们之间相互独立;αA(t),αB(t)和αC(t)为平台干扰信号在天线A,B和C的投射系数;βA(t),βB(t)和βC(t)为宇宙射电信号在天线A,B和C的投射系数。
平台干扰信号比低频射电天文信号大3~10个量级,因此,分离平台干扰是进行有效天文观测的基本前提。
经典的CLEAN算法在脏图或残余图中搜索最大值,此处包含部分真实目标,减去点扩散函数(Point Spread Function, PSF)提取这部分真实目标,不断迭代,直到残余图中只剩噪声结构[20]。CLEAN算法同样可以应用到时域信号,比如利用CLEAN算法对时间序列进行频谱分析[21],识别声源[22],以及提取一些特定结构的信号(周期信号、准周期信号)等[23]。
我们利用CLEAN算法提取低频射电频谱仪的平台干扰信号。算法的输入数据为一组天线的观测数据。首先,计算每个天线的频谱,以及每对天线的互相关功率谱,并将所有的互相关功率谱叠加。由于天线的接收机噪声N(t)相互独立,因此互相关功率谱中的噪声水平降低,而叠加后互相关功率谱的信噪比进一步增强,有利于提取平台干扰信号。
叠加的互相关功率谱包含平台干扰信号对应的频谱成分,同时包括振幅和相位信息。根据这些信息,我们借助CLEAN算法和傅里叶级数展开公式,可以逐一将某个频率成分对应的三角函数信号从时域数据中扣除。考虑到每个天线及接收机的增益不一致,在扣除时每个天线的CLEAN因子是不一样的。
离散傅里叶变换对应的时域及频域信号都是周期信号。如果信号首尾的值不一致,会在傅里叶变换时出现频谱泄漏,导致频率估计出现偏差。通常,实际采集的信号不满足首尾连续的条件,一般可以采用加窗函数避免频谱泄漏。但是加窗函数会导致信号扭曲,幅度值发生变化,假如我们直接采用傅里叶逆变换的方式进行信号分离,则导致较大的偏差。为此,我们引入CLEAN算法,通过加窗函数的方式获得准确的频谱估计;然后在信号分离时,逐步扣除某一个谐波分量,避免信号扭曲,从而把首尾不连续的干扰信号精确分离。
提取大部分平台干扰信号后,残余信号由接收机噪声主导,此时可以停止CLEAN迭代算法。来自宇宙的射电信号幅度往往小于噪声水平,加上小部分平台干扰信号,低频射电天文信号仍然隐藏在接收机噪声中。之后,可以通过对时域信号积分平均,提高残余信号的信噪比,并利用信号随时间的变化特性进一步辨别、分离平台干扰信号和低频射电天文信号,从而实现对干扰的抑制。
2.2 CLEAN算法的流程按照2.1节的思路,用CLEAN算法分离平台干扰信号的流程如图 5。为了更简明清晰地展示算法,我们先考虑两个天线(分别记为A和B)的情形,并且只考虑连续的时域信号。在某一道观测数据中,天线A的时域数据记为fA(t),天线B的时域数据记为fB(t)。

|
| 图 5 CLEAN算法流程图 Fig. 5 CLEAN algorithm flow chart |
相关的公式为
| $ M_{\mathrm{m}}^{A}=\frac{\overline{M^{A}}}{\overline{M^{A B}}} M_{\mathrm{m}}^{A B}, M_{\mathrm{m}}^{B}=\frac{\overline{M^{B}}}{\overline{M^{A B}}} M_{\mathrm{m}}^{A B}, $ | (2) |
其中,MA和MB分别为FrA(ω)与FrB(ω)的平均振幅;MAB为PrAB(ω)的平均振幅。
| $ \begin{gathered} f_{\mathrm{r}}^{A}(t)=f_{\mathrm{r}}^{A}(t)-\delta M_{\mathrm{m}}^{A} \cos \left(\omega_{\mathrm{m}} t+\varphi_{\mathrm{m}}\right), \\ f_{\mathrm{r}}^{B}(t)=f_{\mathrm{r}}^{B}(t)-\delta M_{\mathrm{m}}^{B} \cos \left(\omega_{\mathrm{m}} t+\varphi_{\mathrm{m}}\right), \end{gathered} $ | (3) |
| $ \begin{gathered} f_{\mathrm{mod}}^{A}(t)=f_{\mathrm{mod}}^{A}(t)+\delta M_{\mathrm{m}}^{A} \cos \left(\omega_{\mathrm{m}} t+\varphi_{\mathrm{m}}\right), \\ f_{\mathrm{mod}}^{B}(t)=f_{\bmod }^{B}(t)+\delta M_{\mathrm{m}}^{B} \cos \left(\omega_{\mathrm{m}} t+\varphi_{\mathrm{m}}\right). \end{gathered} $ | (4) |
本算法使用修正振幅MmA和MmB,没有直接采用频谱FrA(ω)和FrB(ω)在频点ωm处的振幅,原因是当信噪比较低时,频谱的振幅由噪声谱振幅主导,而互相关功率谱PrAB(ω)在频点ωm处的振幅MmAB受噪声的影响较小。
我们假定天线A和B的时域信号fA(t)和fB(t)同步。若由于线路补偿没有做好,两个时域信号之间存在时间延迟,那么需要通过交叉相关的方法计算时间延迟,并对时域信号做延迟修正,然后再用CLEAN算法提取平台干扰信号。
通过CLEAN算法分离平台干扰信号之后,得到的残余信号主要成分是接收机噪声,以及隐藏在其中的宇宙射电信号,还有少部分没有扣除的平台干扰信号。此时两个天线残余信号之间的相关系数比较低。通过计算信噪比发现,残余信号中的平台干扰信号和接收机噪声基本在同一量级。这样可以通过积分平均的方式提高残余信号的信噪比,这与传统辐射计的工作原理一致。至于区分平台干扰信号和宇宙射电信号,则要借助3个天线信号随频谱、时间和来波方向变化的规律。
3 低频射电频谱仪数据处理实例 3.1 低频射电频谱仪数据处理流程低频射电频谱仪原始数据由嫦娥四号地面应用系统数据发布中心提供。数据存储在嫦娥四号低频射电频谱仪载荷相关文件夹下,按照0A,0B,01,2A,2B和2C进行分级,每一级数据按照每个月昼一个文件夹进行排列。每个月昼通常有14个文件,其中7个是数据文件,7个是数据采集参数文件,7个数据文件对应一个月昼中7次开机时间段所采集的科学数据。我们在研究不同时间段的数据时,分别读取这7个文件,并结合相应的7个数据采集参数文件,确定每个时段的采集参数。
以第23月昼高频1级时域数据的第1道数据为例,对应的数据文件名为CE4_GRAS_LFRS-TR_SCI_P_20201014020000_20201014140000_0135_B.01,其中GRAS代表地面应用系统;SCI代表科学数据;0135代表这个文件是第135个数据文件;数据结尾的01扩展名代表数据是1级数据,为时域数据。从文件名可以看出,数据采集的时间是从2020年10月14日2点0分0秒到2020年10月14日14点0分0秒,这个时间是世界时,换算为北京时间还需要在小时数上加8。
在数据文件中,数据按照道的顺序依次排列,每道数据由数据头(79字节)和科学数据(8 192字节)组成。其中数据头包含仪器的相关参数,科学数据共有4 096个数据点,每个数据2个字节,由16位无符号整数组成,高字节在前,低字节在后。读取后还需要将整数电压转化为浮点数电压,具体数据形式参考内部技术文档《探月工程嫦娥四号任务着陆器低频射电频谱仪数据预处理方法设计》。第1道数据一共采集了4 096个点,高频数据的采样间隔为0.01 μs,低频数据的采样间隔为0.2 μs。
我们通过Python编程按照道的顺序依次读取数据,将每道4 096个点排成一行,生成一个科学数据矩阵。程序提取每行(每道)数据,分别用CLEAN算法进行处理。
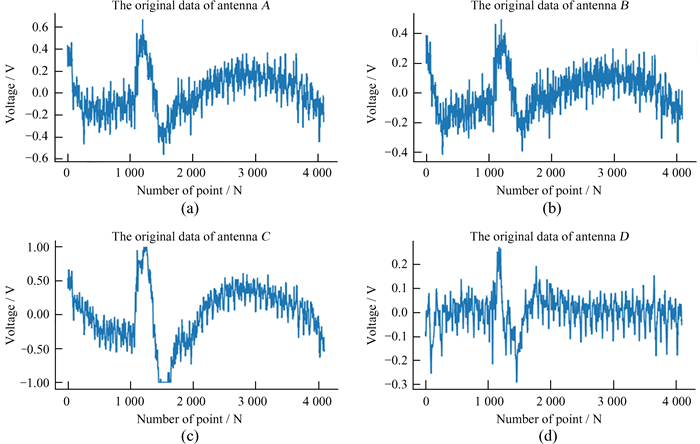
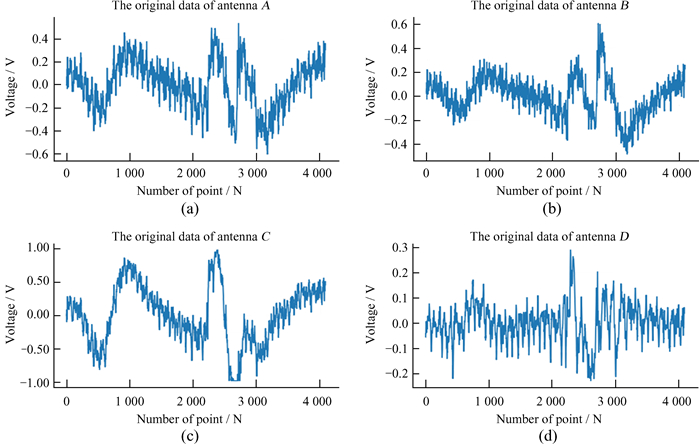
3.2 低频射电频谱仪部分处理结果展示CLEAN算法处理前的时域数据见图 6,由图 6可以看出,天线A和天线B的信号范围基本接近,均为-0.5~0.5 V,天线C数据比天线A和天线B略大。3个天线的信号随时间变化的结构具有较高的相似性,A和B之间的相关系数高达0.965,B和C之间的相关系数为0.823,A和C之间的相关系数为0.915。同时,数据中存在的震荡结构主要成分不是接收机噪声,因为接收机噪声之间无相关性。天线A,B和C信号的均值分别为-0.014 9 V,-0.014 3 V和-0.003 2 V,均接近于0。它们的标准差σ分别为0.189 V,0.138 V和0.409 V,存在明显的差别。这种差别可能是由于3个天线的增益不同,或者平台干扰在3个天线上的投射系数不一致,具体原因有待后续细致的数据分析。从CLEAN算法处理前第2道时域数据(图 7)中可以看到,第1道数据与第2道数据时域信号有较为明显的差别。
|
| 图 6 天线A,B,C和D CLEAN算法处理前的第23月昼第1道原始时域数据。(a)天线A时域数据;(b)天线B时域数据;(c)天线C时域数据;(d)天线D时域数据 Fig. 6 The first time domain data before CLEAN of antenna A, B, C, and D on the 23rd moon day. (a) The time domain data of antenna A; (b) the time domain data of antenna B; (c) the time domain data of antenna C; (d) the time domain data of antenna D |
|
| 图 7 天线A,B,C和D CLEAN算法处理前的第23月昼第2道原始时域数据。(a)天线A时域数据;(b)天线B时域数据;(c)天线C时域数据;(d)天线D时域数据 Fig. 7 The second time domain data before CLEAN of antenna A, B, C and D on the 23rd moon day. (a) The time domain data of antenna A; (b) the time domain data of antenna B; (c) the time domain data of antenna C; (d) the time domain data of antenna D |
从4个天线的数据来看,天线D的响应值比其余3个天线小很多,这是由于天线D长度只有20 cm,比天线A,B和C的长度(5 m)小很多造成的。同时,天线D信号与其余3个天线信号在形状上也有明显的差别,说明天线D的频谱响应明显异于其余3个天线,并且这种差异是非线性的。从天线之间的相关系数也可以看出,天线A,B,C与天线D的数据相关系数分别为0.440,0.397和0.298,显著低于天线A,B和C之间的相关系数。因此,我们放弃使用天线D数据进行平台干扰信号的分离。
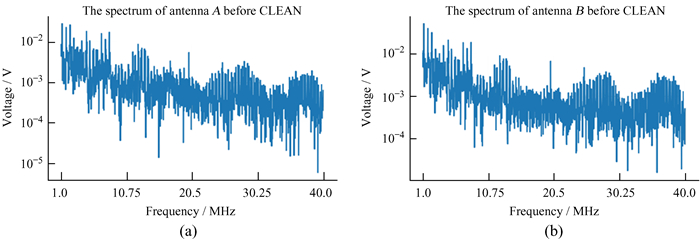
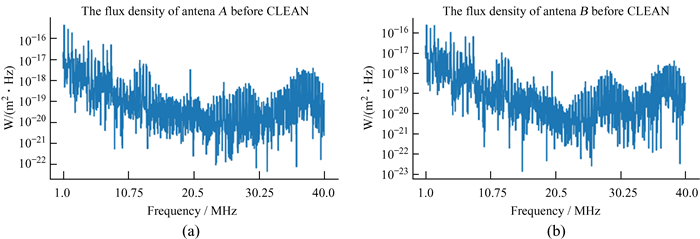
从天线A和天线B CLEAN算法处理前的频谱(图 8)可以看到,频谱的幅度谱强度分布在10-1~10-5 V之间,低频成分强度较大,并且频谱中呈现复杂的结构。将此时的电压频谱转化为流量密度频谱(图 9)后,两天线较低频段的流量密度峰值超过10-16W/(m2·Hz),比太阳爆发信号的流量密度10-18W/(m2·Hz)大2个量级,说明直接读取的时域信号如果不经过去除平台干扰,我们很难发现宇宙射电爆发信号。
|
| 图 8 天线A和天线B CLEAN算法处理前第23月昼第1道数据的频谱。(a)天线A时域数据的频谱;(b)天线B时域数据的频谱 Fig. 8 The spectrum of the first data, before CLEAN, of antenna A and B on the 23rd moon day. (a) The spectrum of antenna A; (b) the spectrum of antenna B |
|
| 图 9 天线A和天线B第23月昼第1道数据CLEAN算法处理前的流量密度。(a)天线A的流量密度;(b)天线B的流量密度 Fig. 9 The first flux density data, before CLEAN, of antennas A and B on the 23rd moon day. (a) The flux density of antenna A; (b) the flux density of antenna B |
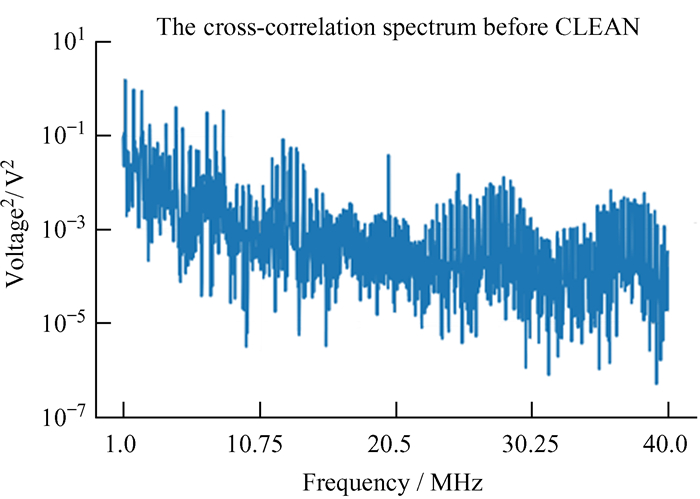
两天线在CLEAN算法处理前的互相关功率谱(图 10)显示,其中存在一些较为复杂的结构。此外,与单天线频谱相比,两天线互相关功率谱的信噪比更高。对比图 10和图 8可以发现,单天线频谱中,低频的峰值比高频的平均值大约高1个数量级,而在两天线互相关功率谱中,低频的峰值比高频的平均值大约高2个数量级。因此,从互相关功率谱出发,更有利于提取平台干扰信号。
|
| 图 10 天线A和天线B CLEAN算法处理前的互相关功率谱 Fig. 10 The cross power spectrum of antennas A and B before CLEAN |
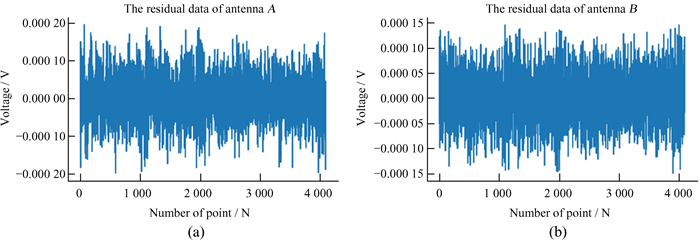
我们进行CLEAN算法处理时选取的δ增益因子为0.2,迭代次数设置为10万次。经过CLEAN算法处理后,天线A和天线B的残余信号显示在图 11中。对比图 8可以看出,CLEAN算法处理前天线时域信号中存在的一些强峰结构已经消失。CLEAN算法处理后天线A数据的标准差为6.58 × 10-5 V,天线B数据的标准差为5.36 × 10-5 V,可见天线数据的波动性已经减小。天线信号在不同时间段的幅度近似相等,这与接收机白噪声本底的特点相符合。
|
| 图 11 天线A和天线B CLEAN算法处理后的残余信号。(a)天线A的残余信号;(b)天线B的残余信号 Fig. 11 The residual signal of antennas A and B after CLEAN. (a) The residual signal of antenna A; (b) the residual signal of antenna B |
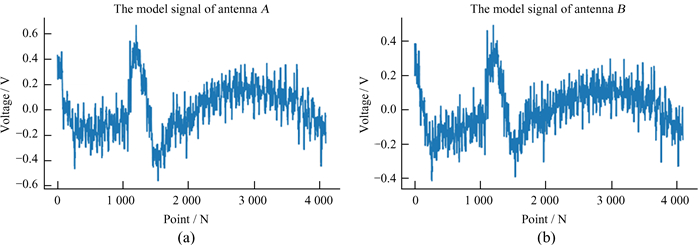
从两天线CLEAN算法处理后得到的模型信号分布(图 12)可以看出,CLEAN算法处理后的模型信号与初始信号很接近,说明原始信号中大部分是平台干扰信号。同时,两天线模型信号的相关系数为0.966,接近1,也说明模型信号中大部分是相关的平台干扰信号。
|
| 图 12 天线A和天线B CLEAN算法处理后的模型信号。(a)天线A的模型信号;(b)天线B的模型信号 Fig. 12 The model signal of antennas A and B after CLEAN. (a) The model signal of antenna A; (b) the model signal of antenna B |
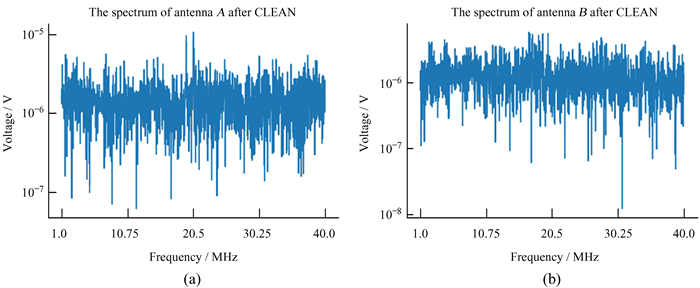
CLEAN算法处理后两天线的频谱(图 13)幅度峰值由原来约10-1V降低到约10-5V,降低4个数量级。残余信号的频谱也不再有明显的频谱结构,在各个频率分量的强度大致相等,可以看作白噪声谱,说明天线信号中的强平台干扰成分得到了非常有效的去除。
|
| 图 13 天线A和天线B CLEAN算法处理后频谱。(a)天线A的频谱;(b)天线B的频谱 Fig. 13 The spectrum of antennas A and B after CLEAN. (a) The spectrum of antenna A; (b) the spectrum of antenna B |
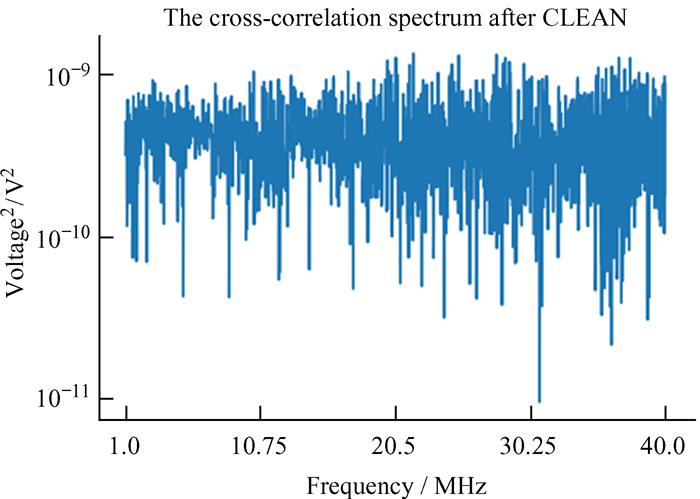
CLEAN算法处理后的互相关功率谱(图 14)同样印证了算法的有效性。由图 14可以看出,两天线的互相关功率谱中已经没有明显的峰值结构,各个频段的互相关功率谱峰值接近10-9V2,对比图 10的结果,降低了约9个数量级。
|
| 图 14 天线A和天线B CLEAN算法处理后的互相关功率谱 Fig. 14 The cross-power spectrum of antennas A and B after CLEAN |
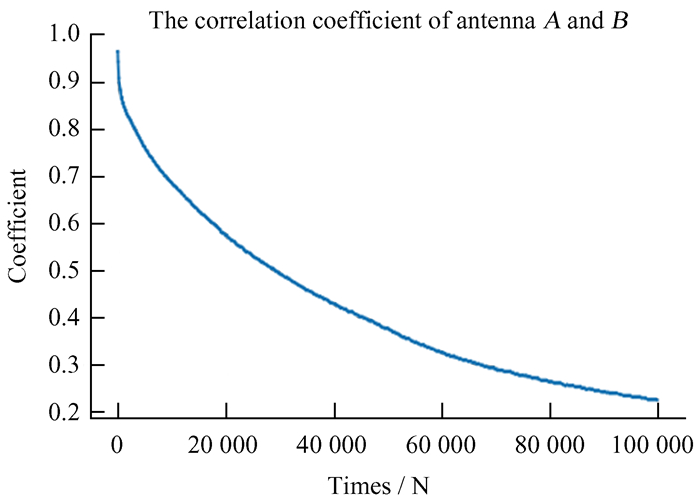
图 15给出了两天线信号之间的相关系数随迭代次数变化的曲线。CLEAN算法处理前初始的相关系数为0.965,由强平台干扰信号主导;CLEAN算法处理10万次后的相关系数接近0.2,根据此相关系数计算的信噪比,可以反映此时残余信号中的平台干扰信号和接收机噪声基本在同一水平,此时信号由接收机噪声主导。当然,CLEAN算法处理结束后,两天线信号的相关系数并没有显著接近0,说明残余信号中可能包含来自宇宙的低频射电信号,以及没有彻底清除的平台干扰信号。
|
| 图 15 天线A和天线B CLEAN算法处理时相关系数随迭代次数分布曲线 Fig. 15 The distribution curve of correlation coefficient between antennas A and B vs. CLEAN iteration |
我们假设天线A和天线B的时域数据分别表示为fA(t)=S(t)+NA(t)和fB(t)=S(t)+NB(t),其中S(t)为完全相同或相关的信号成分,设均值为0,σ记为σS;NA(t)和NB(t)分别表示天线A和天线B的接收机噪声信号,其均值也都为0,σ记为σN,但是,NA(t)和NB(t)是互相独立的。相关系数采用线性相关系数的定义
| $ r = \frac{{{R_{{\rm{SN}}}}^2}}{{{R_{{\rm{SN}}}}^2 + 1}}. $ | (5) |
当相关系数从最初的0.965降低到最后接近0.2时,由(5)式计算得到的信噪比从5.3降低到0.5,说明在末态残余信号中,相干的信号成分和不相干的噪声成分几乎在同一水平。
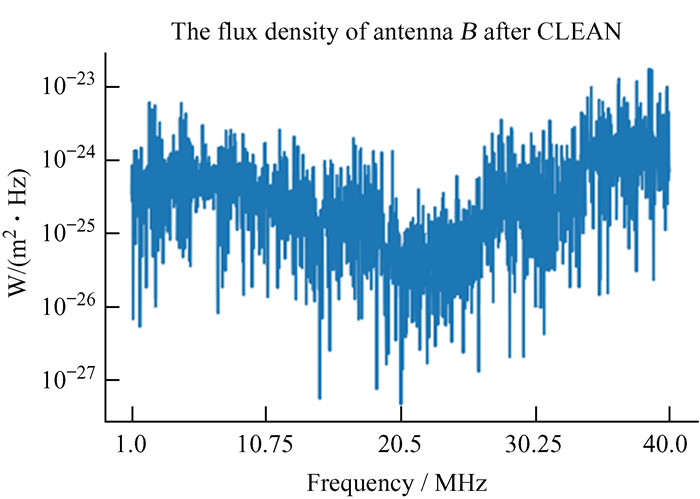
通过将末态信号转化为流量密度,得到天线B末态信号的流量密度随频率的分布(图 16)。从图 16可以看出,末态流量密度基本降低到10-23W/(m2·Hz)以下,与太阳宁静时的信号水平相当。后续可以在此基础上对强射电爆发进行研究。
|
| 图 16 天线B CLEAN算法处理后残余信号的流量密度 Fig. 16 The residual flux density of antenna B after CLEAN |
经过CLEAN算法处理后,嫦娥四号低频射电频谱仪各天线的探测灵敏度(未积分)从10-15W/(m2·Hz)提高到10-23W/(m2·Hz),在此灵敏度下可以对太阳爆发进行监测。太阳爆发的流量密度一般在10-18W/(m2·Hz),极端爆发可以达到10-15W/(m2·Hz)。除此之外,这样的灵敏度也足以探测部分强的快速射电暴,其辐射流量密度可以达到几十万央斯基(Jy),1Jy=10-26W/(m2·Hz)。如果再对时域数据进行积分平均,可以进一步提高探测灵敏度。例如,如果对1道4 096个数据进行积分平均,灵敏度可以提高64倍,大大拓展低频射电频谱仪的科学探测目标。
CLEAN算法分离的平台干扰信号也很有用。首先可以用来分析平台干扰信号的频谱、空间和时间变化特征,并确定其来源,以便在今后开发类似设备时,改进电磁兼容设计,大幅度降低平台干扰水平。其次,在全面了解平台干扰信号特征的基础上,充分利用这些知识,发现特征异常的信号,这些异常信号往往来自宇宙。
分离并抑制干扰信号的最终目的是进行有效的天文观测。如何在强烈的平台干扰背景下寻找并确认宇宙射电信号呢?主要思路是寻找异常信号。平台干扰往往有固定的一组频谱特征,一旦有例外的频谱信号出现,可能意味着记录了来自宇宙的射电爆发信号。如果这些频谱还具备色散等特征,那么几乎可以肯定它来自宇宙。再例如,天线A,B和C信号的强度比例系数,若平台干扰信号产生的空间分布是固定的,那么不管其在时域如何变化,信号之间的强度比例系数也是固定的。倘若这些比例系数有明显的改变,则往往意味着天线接收到来自宇宙的强射电爆发信号。若射电爆发信号的时标长达几天量级,这些比例系数还会随着月球自转发生规律性变化,有助于我们更加可靠地确定爆发信号的来源。当然,具体如何搜寻异常信号,还得依赖后续细致的数据分析工作。
本文提出的算法也可以应用到其他射电观测设备,尤其是地基综合射电干涉阵。目前地基干涉阵受到越来越多的来自地面设备以及空间卫星的无线电干扰。借助CLEAN算法,我们利用两天线之间的互相关功率谱,在信号层面提取干扰信号,再对残余信号数据相关获得可见度数据,对可见度数据作成图等处理工作。同样,我们也可以对提取的干扰信号进行类似的操作,获得详细的频谱、空间分布和时域变化等信息。
5 结论本文提出一种CLEAN算法,从两组信号的相关性出发,并借助互相关功率谱、傅里叶级数等工具,把低频射电频谱仪天线A,B和C的时域观测数据分为强相关的CLEAN模型信号和部分相关的残余信号。其中CLEAN模型信号主要由平台干扰信号和可能的低频强射电爆发组成;残余信号由接收机噪声、未扣除的平台干扰信号和常规低频射电信号组成。将该算法应用到实际数据中,结果表明,嫦娥四号低频射电频谱仪的未积分灵敏度可以提高约8个数量级,达到10-23W/(m2·Hz)。
在此基础上,基于对平台干扰信号中确定成分和宽带随机成分的分类处理,再借助低频射电爆发信号和平台干扰信号在功率谱上不同的表现,以及常规低频射电信号受月球自转调制等信息,将来工作的重点是进一步分析CLEAN模型信号和残余信号,以期搜索低频强射电爆发信号,乃至对全天区进行粗略成像。
| [1] |
梅丽, 苏彦, 周建锋. 极低频射电天文观测现状与未来发展[J]. 天文研究与技术, 2018, 15(2): 127–149 MEI L, SU Y, ZHOU J F. The history and development of the low-frequency radio observation[J]. Astronomical Research & Technology, 2018, 15(2): 127–149. |
| [2] | LESHEM A, VAN DER VEEN A J, DEPRETTERE E. Detection and blanking of GSM interference in radio-astronomical observations[C]// Proceedings of the 2nd IEEE Workshop on Signal Processing Advances in Wireless Communications. 1999: 374-377. |
| [3] | FRIDMAN P A, BAAN W A. RFI mitigation methods in radio astronomy[J]. Astronomy & Astrophysics, 2001, 378(1): 327–344. DOI: 10.1051/0004-6361:20011166 |
| [4] | ELLINGSON S W, BUNTON J D, BELL J F. Removal of the GLONASS C/A signal from OH spectral line observations using a parametric modeling technique[J]. The Astrophysical Journal Supplement Series, 2001, 135(1): 87. DOI: 10.1086/321780 |
| [5] | ELLINGSON S W. Beamforming and interference canceling with very large wideband arrays[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(6): 1338–1346. DOI: 10.1109/TAP.2003.812237 |
| [6] | BARNBAUM C, BRADLEY R F. A new approach to interference excision in radio astronomy: real-time adaptive cancellation[J]. The Astronomical Journal, 1998, 116(5): 2598. DOI: 10.1086/300604 |
| [7] | BRIGGS F H, BELL J F, KESTEVEN M J. Removing radio interference from contaminated astronomical spectra using an independent reference signal and closure relations[J]. The Astronomical Journal, 2000, 120(6): 3351. DOI: 10.1086/316861 |
| [8] | LESHEM A, VAN DER VEEN A J, BOONSTRA A J. Multichannel interference mitigation methods in radio astronomy[J]. The Astrophysical Journal Supplement Series, 2000, 131(1): 355. DOI: 10.1086/317360 |
| [9] | FRIEDMAN P. A change point detection method for elimination of industrial interference in radio astronomy receivers[C]// Proceedings of the 8th Workshop on Statistical Signal and Array Processing. 1996: 264-266. |
| [10] | WEBER R, FAYE C, BIRAUD F, et al. Spectral detector for interference time blanking using quantized correlator[J]. Astronomy & Astrophysics Supplement Series, 1997, 126(1): 161–167. |
| [11] | MASLAKOVIC S, LINSCOTT I R, OSLICK M, et al. Excising radio frequency interference using the discrete wavelet transform[C]// Proceedings of the third International Symposium on Time-Frequency and Time-Scale Analysis. 1996: 349-352. |
| [12] | KASPER B L, CHUTE F S, ROUTLEDGE D. Excising terrestrial radio interference in low frequency radio astronomy[J]. Monthly Notices of the Royal Astronomical Society, 1982, 199(2): 345–354. DOI: 10.1093/mnras/199.2.345 |
| [13] | BAAN W A, FRIDMAN P A, MILLENAAR R P. Radio frequency interference mitigation at the westerbork synthesis radio telescope: algorithms, test observations, and system implementation[J]. The Astronomical Journal, 2004, 128(2): 933–949. DOI: 10.1086/422350 |
| [14] | OFFRINGA A R, DE BRUYN A G, BIEHL M, et al. Post-correlation radio frequency interference classification methods[J]. Monthly Notices of the Royal Astronomical Society, 2010, 405(1): 155–167. DOI: 10.1111/j.1365-2966.2010.16471.x |
| [15] | ZHAO J, ZOU X, WENG F. WindSat radio-frequency interference signature and its identification over Greenland and Antarctic[J]. IEEE Transactions on Geoscience & Remote Sensing, 2013, 51(9): 4830–4839. |
| [16] | WOLFAARDT C J. Machine learning approach to radio frequency interference (RFI) classification in radio astronomy[D]. Stellenbosch: Stellenbosch University, 2016. |
| [17] |
张韬, 苏彦. 嫦娥四号低频射电频谱仪降低背景噪声方法的研究[J]. 天文研究与技术, 2019, 16(3): 312–320 ZHANG T, SU Y. Research of the method for reducing background of very low frequency radio spectrumon Chang'E-4[J]. Astronomical Research & Technology, 2019, 16(3): 312–320. DOI: 10.3969/j.issn.1672-7673.2019.03.008 |
| [18] | BASTIAN T S, BENZ A O, GARY D E. Radio emission from solar flares[J]. Annual Review of Astronomy and Astrophysics, 1998, 36(1): 131–188. DOI: 10.1146/annurev.astro.36.1.131 |
| [19] | BOCHENEK C D, RAVI V, BELOV K V, et al. A fast radio burst associated with a Galactic magnetar[J]. Nature, 2020, 587(7832): 59–62. DOI: 10.1038/s41586-020-2872-x |
| [20] | HÖGBOM J A. Aperture synthesis with a non-regular distribution of interferometer baselines[J]. Astronomy & Astrophysics Supplement Series, 1974, 15: 417. |
| [21] | HESLOP D, DEKKERS M J. Spectral analysis of unevenly spaced climatic time series using CLEAN: signal recovery and derivation of significance levels using a Monte Carlo simulation[J]. Physics of the Earth and Planetary Interiors, 2002, 130(1/2): 103–116. DOI: 10.1016/S0031-9201(01)00310-7 |
| [22] | COUSSON R, LECLERE Q, PALLAS M A, et al. A time domain CLEAN approach for the identification of acoustic moving sources[J]. Journal of Sound and Vibration, 2019, 443: 47–62. DOI: 10.1016/j.jsv.2018.11.026 |
| [23] | KULPA K. The CLEAN type algorithms for radar signal processing[C]// Proceedings of the 2008 Microwaves, Radar and Remote Sensing Symposium. 2008: 152-157. |



