2. 广西相对论天体物理重点实验室,广西 南宁 530004;
3. 广西大学物理科学与工程技术学院,广西 南宁 530004
2. Guangxi Key Laboratory for the Relativistic Astrophysics, Nanning 530004, China;
3. School of Physical Science and Engineering Technology, Guangxi University, Nanning 530004, China
活动星系核(Active Galactic Nuclei, AGN)是一类特殊的星系,在活动星系核中存在剧烈程度超过恒星内部核反应的高能伽马射电非热辐射过程和猛烈的物质喷射等活动现象,其中耀变体(Blazar)是活动星系核的一个子类,耀变体又分为蝎虎座BL型天体(BL Lac)和平谱射电类星体(Flat Spectrum Radio Quasars, FSRQ)。蝎虎天体和平谱射电类星体的区分依据是发射线的强弱,发射线比较弱或没有的是蝎虎天体,比较强的是平谱射电类星体。耀变体具有大幅快速的光变、比较高的辐射偏振和非热连续光谱等特征[1]。绝大部分耀变体的光变具有随机性,而具有准周期性光变的耀变体极少,但是也有文献报道了少数准周期候选体。随着观测技术的进步和数据的积累,研究人员不断发现新的候选体。其中最著名的是文[2]在1988年发现OJ 287在光学V波段具有大约12年的周期性爆发,这一周期性爆发现象可以用超大质量双黑洞模型解释。4年后,文[3]分析了OJ 287光学B波段100多年的数据,发现B波段爆发周期为11.6 ± 0.5年,证实了文[2]的结论,并预测下一次爆发最大值出现在1994年8月左右。随后越来越多的科研工作者参与准周期搜寻,文[4]发现PG 1553+113在光学和伽马波段具有2.18 ± 0.08年的准周期震荡;文[5]用多种方法分析LAT(Fermi Large Area Telescope)数据,发现11个活动星系核存在准周期震荡,其中9个是首次发现;文[6]发现3FGL J0449.4-4350在光学和伽马波段存在450天左右的准周期震荡,基于超大质量双黑洞模型估算了其主黑洞质量,约为7.7 × 109M⊙;文[7]发现耀变体CGRaBS J0835+6835的射电波段存在560天左右的光变准周期,并用螺旋喷流模型估算主黑洞质量在3.7 × 108M⊙~3.5 × 109M⊙之间。
在欧文斯谷射电天文台(Owens Valley Radio Observatory, OVRO)40 m射电望远镜和费米伽马射线太空望远镜(Fermi Gamma-ray Space Telescope)的观测数据库中,我们用时间序列分析法进行准周期信号的搜索。搜索结果表明,蝎虎天体CGRaBS J0929+5013(4FGL J0929.3+5014)和平谱射电类星体CGRaBS J2146-1525(4FGL J2146.4-1528)可能存在准周期震荡,因此,我们对J0929+5013和J2146-1525射电和伽马波段的数据做了进一步分析,探究两个波段之间的光变相关性以及辐射机制。J0929+5013(α=09 29 15.4400532384, δ=+50 13 35.987058917)是一颗红移z=0.370 39的天体,在B,V波段的流量分别为0.000 49 mJy和0.000 69 mJy[8]。J2146-1525(α=21 46 22.97933395, δ=-15 25 43.8856129)是一颗z=0.70[9]的天体,在B,V波段的流量分别为0.000 30 mJy和0.000 45 mJy[8]。
1 数据分析我们分别从欧文斯谷射电天文台40 m射电望远镜的官网(https://sites.astro.caltech.edu/ovroblazars/)和费米伽马射线太空望远镜官网(Fermi-LAT, https://fermi.gsfc.nasa.gov/ssc/data/access/lat/10yr_catalog/ap_lcs.php)的观测数据中收集了J0929+5013(J0929.3+5014)和J2146-1525(J2146.4-1528)15 GHz射电波段和0.1~200 GeV伽马波段约12年的数据。40 m望远镜配备了离轴双光束系统以减少不断变化的大气辐射,并在主焦点安装一个冷却接收器,带宽为3 GHz,中心频率为15 GHz。该望远镜对每个射电源每周监测大约两次。伽马射线数据来源于孔径测光法(测光半径为1°,最大天顶角105°),因此并没有去掉伽马射线背景光子,但是背景光子流量比较稳定,对光变分析的影响可以忽略不计(我们对J0929+5013和J2146-1525伽马波段的数据用费米工具包处理,得到7天、10天和30天时段的数据,用LSP方法和加权小波Z变换方法计算得到的结果基本相同),因此本文选取30天时段的数据。我们采用光变指数A判断天体的活跃程度[10],
| $ A=\frac{f_{\max }-f_{\min }}{f_{\max }+f_{\min }} . $ | (1) |
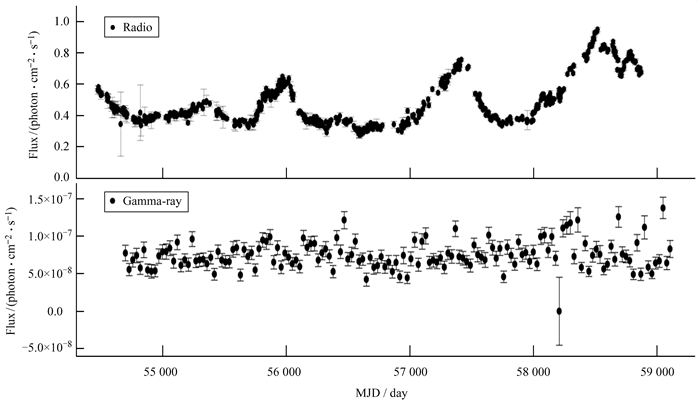
其中,fmax为流量的最大值;fmin为流量的最小值。通过计算可以得到J0929+5013和J2146-1525射电波段的光变指数分别为0.55和0.35,伽马波段的光变指数分别为0.53和0.46。光变指数越接近1,天体越活跃,J0929+5013和J2146-1525在射电和伽马波段比较活跃。图 1是J0929+5013在射电和伽马波段的光变曲线,图 2是J2146-1525在射电和伽马波段的光变曲线。横坐标为简化儒略日(Modified Julian Day, MJD),纵坐标为流量及误差(大部分误差很小,图中不能清晰分辨)。
|
| 图 1 CGRaBS J0929+5013在射电和伽马波段的光变曲线 Fig. 1 The light curves of CGRaBS J0929+5013 in radio and gamma-ray wave bands |
|
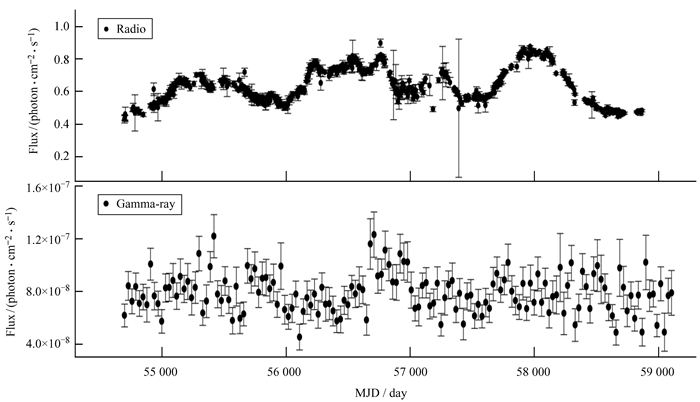
| 图 2 CGRaBS J2146-1525在射电和伽马波段的光变曲线 Fig. 2 The light curves of CGRaBS J2146-1525 in radio and gamma-ray wave bands |
耀变体的周期性光变研究,对理解其内部辐射的物理机制和辐射区的几何性质有重要意义。LSP方法基于傅里叶变换,使用正弦函数模型,可以对非均匀采样的时间序列周期图进行相位修正,在一定范围内对非均匀采样的时间间隔引起的误报周期进行修正,寻找隐藏在噪声中的准周期振荡。基本公式[11]为
| $ p_{x}(\omega)=\frac{1}{2}\left\{\frac{\sum\limits_{j=1}^{N}\left[x\left(t_{j}\right)-\bar{x}\right] \cos \omega\left(t_{j}-\tau\right)}{\sum\limits_{j=1}^{N} \cos ^{2} \omega\left(t_{j}-\tau\right)}+\frac{\sum\limits_{j=1}^{N}\left[x\left(t_{j}\right)-\bar{x}\right] \sin \omega\left(t_{j}-\tau\right)}{\sum\limits_{j=1}^{N} \sin ^{2} \omega\left(t_{j}-\tau\right)}\right\}, $ | (2) |
其中,tj为时间序列的平均值;N为数据点的个数;τ为相应的时间相位修正,
| $ \tan (2 \omega \tau)=\frac{\sum\limits_{j=1}^{N} \sin ^{2} 2 \omega t_{j}}{\sum\limits_{j=1}^{N} \cos ^{2} 2 \omega t_{j}}. $ | (3) |
我们对LSP方法计算的结果用蒙特卡洛模拟进行置信度评估[12],对LSP做对数幂率拟合,得到J0929+5013在射电和伽马波段的幂率指数[13]分别为β=0.5和β=0.1;J2146-1525在射电和伽马波段的幂率指数分别为β=0.7和β=0.3。幂率指数值偏小,我们认为主要原因可能是受白噪声影响,在相当一部分情况下,幂率指数大约为1 [14]。
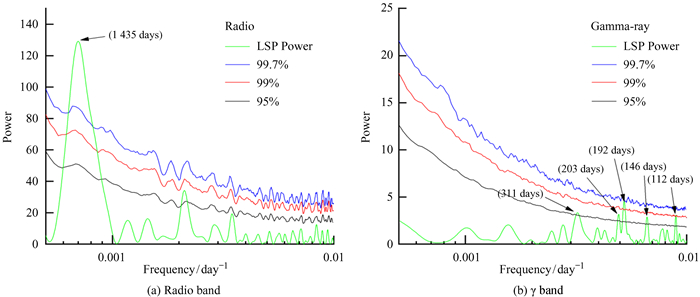
图 3和图 4分别是J0929+5013和J2146-1525在射电和伽马波段准周期振荡的蒙特卡罗置信度分析结果,其中绿色线表示准周期频率图,峰值就是准周期频率,黑色、红色和蓝色线分别表示蒙特卡罗模拟的2σ(95%),2.6σ(99%)和3σ(99.7%)置信度曲线。
|
| 图 3 CGRaBS J0929+5013在射电(β=1)和伽马(β=1)波段准周期震荡的蒙特卡罗置信度分析结果 Fig. 3 The confidence analysis results of quasi periodic oscillation of CGRaBS J0929+5013 in radio (β=1) and gamma-ray (β=1) wave bands by Monte Carlo simulation |
|
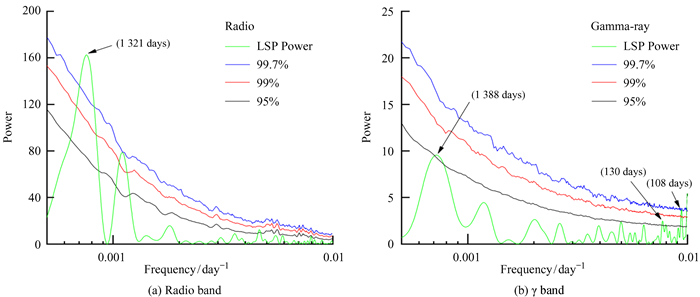
| 图 4 CGRaBS J2146-1525在射电(β=1.5)和伽马(β=1)波段准周期震荡的蒙特卡罗置信度分析结果 Fig. 4 The confidence analysis results of quasi periodic oscillation of CGRaBS J2146-1525 in radio (β=1.5) and gamma-ray (β=1) wave bands by Monte Carlo simulation |
图 3(a)和(b)分别表示J0929+5013在射电和伽马波段的蒙特卡罗置信度分析结果。通过计算得到J0929+5013在射电波段有一个1 435天(约3.93年)的置信度>3σ的准周期,在伽马波段有5个置信度>2σ的峰,其中112,146和203约为53.4天(卫星的进动周期)2倍、3倍和4倍,我们推测它们是飞船进动引起的高次谐频,192天约为半年,也是一个谐频。我们认为311天可能是伽马波段一个很弱的准周期,有待进一步确认。
如图 4(a)和(b),J2146-1525在射电波段有一个1 321天(约3.62年)的置信度>3σ的准周期,在伽马波段有3个置信度>2σ的峰,其中108天约为53.4天的2倍,130天约为月亮周期27.3天的4倍。我们认为1 388天可能是伽马波段一个很弱的准周期,有待进一步确认。
3 加权小波Z变换周期分析小波分析(Wavelet Analysis)是一种由傅里叶变换演化而来的分析方法,能将时域和频域局部化,通过平移和伸缩变换可以把小波母函数变为小波函数[15]:
| $ \psi_{a, b}(t)=\frac{1}{\sqrt{a}} \psi\left(\frac{t-b}{a}\right), $ | (4) |
其中,a和b分别为伸缩尺度和平移参数。Foster定义了加权小波变换:
| $ W W T=\frac{\left(N_{\text {eff }}-1\right) V_{\mathrm{y}}}{2 V_{\mathrm{x}}}, $ | (5) |
其中,Neff为有效数据点个数;Vx为数据的加权偏差;Vy为模型函数的加权偏差。这种原理在低频部分分辨率很高,导致低频部分有效数据Neff多于高频部分,所以加权小波变换的值倾向于高频部分,因此Foster按照Z统计量对加权小波Z变换[16]进行了定义:
| $ Z=\frac{\left(N_{\mathrm{eff}}-3\right) V_{\mathrm{y}}}{2\left(V_{\mathrm{x}}-V_{\mathrm{y}}\right)}. $ | (6) |
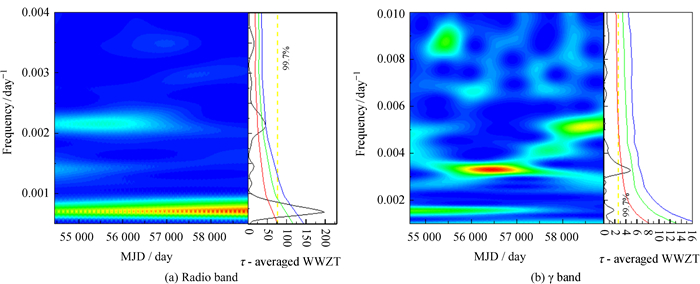
我们根据加权小波Z变换的基本原理,编写Python程序处理J0929+5013和J2146-1525在射电和伽马波段的数据。图 5和图 6中黑色曲线为周期的函数图,其中红色、绿色和蓝色线分别表示基于红噪声的2σ,2.6σ和3σ置信概率线,黄色虚线表示基于白噪声的99.7%置信概率线。根据加权小波Z变换图中的极大值可以确定光变准周期。
|
| 图 5 CGRaBS J0929+5013在射电和伽马波段准周期震荡的加权小波Z变换方法分析结果 Fig. 5 The WWZT test result for quasi periodic oscillation CGRaBS J0929+5013 at radio and gamma-ray wave bands |
|
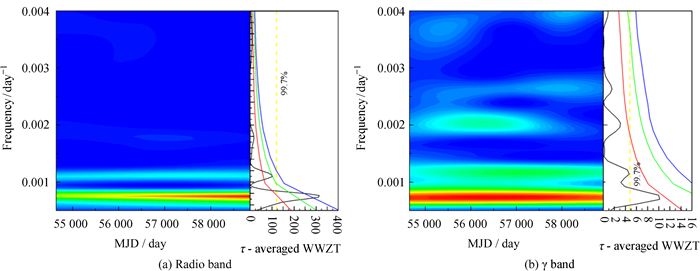
| 图 6 CGRaBS J2146-1525在射电和伽马波段准周期震荡的加权小波Z变换方法分析结果 Fig. 6 The WWZT test result for quasi periodic oscillation search CGRaBS J2146-1525 at radio and gamma-ray wave bands |
图 5(a)和(b)分别表示J0929+5013在射电和伽马波段用加权小波Z变换法计算的结果,(a)图显示J0929+5013在射电波段存在一个置信度>3σ的极大值1 435.0天(约3.93年),(b)图显示J0929+5013在伽马波段存在一个置信度>2σ的极大值306.7天(约0.84年)。J0929+5013在射电和伽马波段基于白噪声的置信度都>3σ,这是一个比较强的假设。我们认为J0929+5013在射电波段存在一个1 435.0天的比较可信的准周期,在伽马波段306.7天的准周期还需进一步确认。
如图 6(a)和(b),J2146-1525在射电波段存在一个置信度>3σ的极大值1 320.5天(约3.61年),在伽马波段存在一个极大值1 384.8天(约3.80年),在射电和伽马波段基于白噪声的置信度都>3σ。我们认为J2146-1525在射电波段存在一个1 320.5天的比较可信的准周期,在伽马波段1 384.8天的准周期还需进一步确认。
4 相关性分析上面我们已经用不同的方法计算了J0929+5013和J2146-1525在射电和伽马波段的准周期,同一个天体不同波段的光变有没有相关性呢?为了研究这个问题,我们用离散相关函数法(Discrete Correlation Function, DCF)分别对J0929+5013和J2146-1525的射电和伽马波段数据做相关性分析。离散相关函数比较适合分析时域分布不均匀的天文观测数据[17],基本公式为
| $ U D C F_{i j}=\frac{\left(a_{i}-\bar{a}\right) \times\left(b_{i}-\bar{b}\right)}{\sigma_{a}-\sigma_{b}}, $ | (7) |
其中,a和b分别表示两组数据的平均值;σa和σb为两组数据的标准偏差。
| $ D C F(\tau)=\frac{1}{M} \sum U D C F_{i j}, $ | (8) |
将(7)式代入(8)式,得到相关系数。
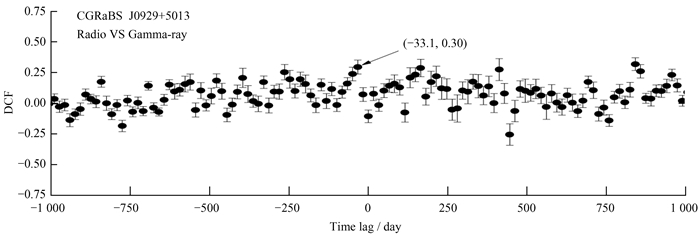
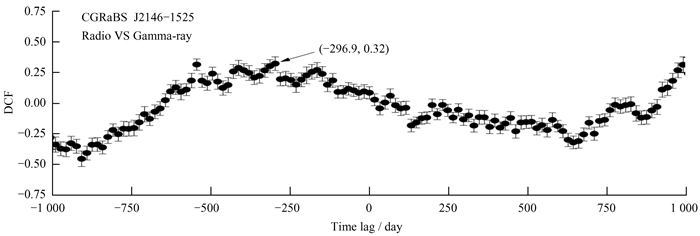
图 7和图 8分别是J0929+5013和J2146-1525在射电和伽马波段的相关性分析结果。从图中可以看出,相关系数的最大值仅为0.32和0.30。相关性在0.5~1之间两者才可能存在相关性,因此,J0929+5013和J2146-1525在射电和伽马波段都没有明显的相关性。我们认为两个波段的辐射可能来自不同的区域。
|
| 图 7 CGRaBS J0929+5013在射电和伽马波段相关性分析结果 Fig. 7 The DCF analysis result of CGRaBS J0929+5013 in radio and gamma-ray wave bands |
|
| 图 8 CGRaBS J2146-1525在射电和伽马波段相关性分析结果 Fig. 8 The DCF analysis result of CGRaBS J2146-1525 in radio and gamma-ray wave bands |
我们用LSP方法和加权小波Z变换方法对J0929+5013和J2146-1525在射电和伽马波段的数据进行分析,得到J0929+5013在射电波段存在一个置信度>3σ约1 435天的准周期光变,在伽马波段存在置信度>2σ的很弱的309天左右的准周期。离散相关函数法分析两个波段的相关性发现,这两个波段没有明显的相关性,我们认为两个波段的辐射来自不同的区域。J0929+5013在射电波段存在一个置信度>3σ约1 321天的准周期光变,在伽马波段也存在一个很弱的1 385天的可能准周期光变。同样,我们用离散相关函数法对两个波段的数据做相关性分析,结果表明,这两个波段的相关性也很弱。由于数据点有限,以及光变曲线的时间跨度不够长,大约只有所测准周期振荡时标的4倍,我们给出的只是两个准周期振荡候选体。耀变体中准周期振荡是非常罕见的,因此,需要更长时间和更多的数据来证实。
对于耀变体准周期振荡的起源和理论解释都还存在争议。目前,主要的解释有3种:(1)双黑洞引起的螺旋喷流模型[18];(2)单黑洞的吸积盘脉动模型[19];(3)单黑洞引起的喷流进动模型[20]。我们基于双黑洞螺旋喷流模型对J0929+5013和J2146-1525的质量做了估算,根据文[21]在2004年给出的观测运动准周期P与实际物理驱动周期Pd之间的关系
| $ P_{\mathrm{d}} \approx \frac{\gamma_{\mathrm{b}}^{2}}{1+z} P, $ | (9) |
其中,γb为体洛伦兹因子,约等于7.5[22];P的单位为年。我们用比较可信的射电波段的观测准周期,它们分别为3.93年和3.62年,红移分别为0.37和0.70。J0929+5013和J2146-1525的实际物理驱动周期分别为161.36年和119.78年。如果主黑洞和次黑洞之间的质量比R≤1/3,称之为“主并合”;如果3≤R≤104,称之为“次并合”[23]。主黑洞的质量估算公式为[24]
| $ M \approx P_{\mathrm{d}}^{\frac{8}{5}} R^{\frac{3}{5}} 10^{6} M_{\odot}, $ | (10) |
其中,假设主次黑洞质量比为R=3/2。我们把参数代入(10)式,得到J0929+5013和J2146-1525主黑洞质量分别约为4.3 × 109M⊙和2.7 × 109M⊙。同理,如果使用γb=15[25]作为参数,次并合的超大质量双黑洞系统的主黑洞质量分别为4.0 × 1010M⊙和2.5 × 1010M⊙,故J0929+5013和J2146-1525主黑洞质量M分别为4.3 × 109M⊙和2.7 × 109M⊙。
| [1] | URRY C M, PADOVANI P. Unified schemes for radio-loud Active Galactic Nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107: 803. DOI: 10.1086/133630 |
| [2] | SILLANPÄÄ A, HAARALA S, VALTONEN M J, et al. OJ 287-binary pair of supermassive black holes[J]. The Astrophysical Journal, 1988, 325(2): 628–634. DOI: 10.1086/166033 |
| [3] | KIDGER M, TAKALO L, SILLANPÄÄ A. A new analysis of the 11-year period in OJ287-confirmation of its existence[J]. Astronomy & Astrophysics, 1992, 264(1): 32–36. DOI: 10.1086/116351 |
| [4] | ACKERMANN M, MAX-MOERBECK W, PEARSON T J, et al. Multiwavelength evidence for quasi-periodic modulation in the gamma-ray blazar PG 1553+113[J]. The Astrophysical Journal Letters, 2016, 831(2): L41. |
| [5] | PENIL P, DOMINGUEZ A, BUSON S, et al. Systematic search for γ-ray periodicity in active galactic nuclei detected by the Fermi Large Area Telescope[J]. The Astrophysical Journal, 2020, 896(2): 134. DOI: 10.3847/1538-4357/ab910d |
| [6] | YANG X, YI T F, ZHANG Y, et al. The γ-ray and optical variability analysis of the BL Lac Object 3FGL J0449.4-4350[J]. Publications of the Astronomical Society of the Pacific, 2020, 132(1010): 1538–1548. DOI: 10.1088/1538-3873/ab779e |
| [7] |
龚云露, 易庭丰, 杨星, 等. 耀变体CGRaBS J0835+6835的射电准周期振荡及多普勒因子分析[J]. 天文研究与技术, 2021, 18(2): 145–152 GONG Y L, YI T F, YANG X, et al. Radio quasi-period oscillation analysis of blazar CGRaBS J0835+6835[J]. Astronomical Research & Technology, 2021, 18(2): 145–152. |
| [8] | VÉRON-CETTY M P, VÉRON P. A catalogue of quasars and active nuclei: 13th edition[J]. Astronomy & Astrophysics, 2010, 518: A10. DOI: 10.1051/0004-6361/201014188 |
| [9] | TRUEBENBACH A E, DARLING J. The VLBA extragalactic proper motion catalog and a measurement of the secular aberration drift[J]. The Astrophysical Journal Supplement, 2017, 233(1): 3. DOI: 10.3847/1538-4365/aa9026 |
| [10] | LI H Z, XIE G Z, CHEN L E, et al. The periodicity analysis of the light curve of 3C 279 and implications for the precession jet[J]. Publications of the Astronomical Society of the Pacific, 2009, 121: 1172–1179. DOI: 10.1086/648433 |
| [11] | LOMB N R. Least-squares frequency analysis of unequally spaced data[J]. Astrophysics & Space Science, 1976, 39(2): 447–462. DOI: 10.1007/BF00648343 |
| [12] | REJKUBA M, MINNITI D, SILVA D R, et al. Long period variables in NGC 5128: Ⅱ. near-IR properties[J]. Astronomy & Astrophysics, 2003, 411(3): 351–360. |
| [13] | TIMMER J, KOENIG M. On generating power law noise[J]. Astronomy & Astrophysics, 1995, 300: 707–710. |
| [14] | COVINO S, SANDRINELLI A, TREVES A. Gamma-ray quasi-periodicities of blazars. A cautious approach[J]. Monthly Notices of the Royal Astronomical Society, 2019, 482(1): 1270–1274. DOI: 10.1093/mnras/sty2720 |
| [15] | GROSSMANN A, MORLET J. Decomposition of hardy functions into square integrable wavelets of constant shape[J]. Siam Journal on Mathematical Analysis, 1984, 15(4): 723–736. DOI: 10.1137/0515056 |
| [16] | FOSTER G. Wavelets for period analysis of unevenly sampled time series[J]. The Astronomical Journal, 1996, 112(4): 1709. |
| [17] |
龚云露, 易庭丰, 杨星. 平谱射电类星体3C 273在γ射线、射电和光学波段的相关性分析[J]. 玉溪师范学院学报, 2019, 35(6): 69–73 GONG Y L, YI T F, YANG X. Correlation analysis of flat-spectrum radio quasar 3C 273 in gamma ray, radio and optical band[J]. Journal of Yuxi Normal University, 2019, 35(6): 69–73. DOI: 10.3969/j.issn.1009-9506.2019.06.012 |
| [18] | VALTAOJA E, TERSRANTA H, TORNIKOSKI M, et al. Radio monitoring of OJ 287 and binary black hole models for periodic outbursts[J]. The Astrophysical Journal, 2008, 531(2): 744. |
| [19] | WALLINDER F H, KATO S, ABRAMOWICZ M A. Variability of the central region in active galactic nuclei[J]. The Astronomy & Astrophysics Review, 1992, 4(2): 79–122. |
| [20] | MARSCHER A P. Contemporaneous X-ray and VLBI radio observations of the quasar NRAO 140[J]. The Astrophysical Journal, 1988, 334(2): 552–559. |
| [21] | LHTEENMKI A, VALTAOJA E, WⅡK A K. Total flux density variations in extragalactic radio sources. Ⅱ. Determining the limiting brightness temperature for synchrotron sources[J]. The Astrophysical Journal, 2009, 511(1): 112–117. |
| [22] | HENRI G, SAUGÉ L. The bulk Lorentz factor crisis of TeV blazars: evidence for an inhomogeneous pileup energy distribution?[J]. The Astrophysical Journal, 2006, 640(1): 185–195. DOI: 10.1086/500039 |
| [23] | BEGELMAN M C, BLANDFORD R D, REES M J. Massive black hole binaries in active galactic nuclei[J]. Nature, 1980, 287(5780): 307–309. DOI: 10.1038/287307a0 |
| [24] | LEE W H, ABRAMOWICZ M A, KLUZNIAK W. Resonance in forced oscillations of an accretion disk and kilohertz quasi-periodic oscillations[J]. The Astrophysical Journal Letters, 2004, 603: L93–L96. DOI: 10.1086/383245 |
| [25] | GUINEVERE K, MARTIN H. A unified model for the evolution of galaxies and quasars[J]. Monthly Notices of the Royal Astronomical Society, 2000, 311(3): 576–588. DOI: 10.1046/j.1365-8711.2000.03077.x |



