2. 中国科学院大学, 北京 100049;
3. 中国科学技术大学物理学院, 安徽 合肥 230026
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Physical Sciences, University of Science and Technology of China, Hefei 230026, China
引力N体模拟是研究星系、暗物质晕以及宇宙大尺度结构等天文系统形成和演化的主要方法之一。由于引力是长程力,对于星系以及更大尺度或更多粒子数的引力系统,可以把成员恒星(或暗物质粒子)的运动看作是总体引力势下的运动,而不需要考虑恒星之间的相互作用,即无碰撞引力系统,也是一种平均场近似的思想。对这类系统随时间演化的N体数值模拟,可以不考虑N体粒子两两之间的引力作用,仅计算共同的引力场,以及引力场对具体粒子的作用,即无碰撞引力N体数值模拟[1]。在近来的应用中(Gadget-3, Gadget-4),PM-Tree方法是无碰撞引力N体模拟的主要方法之一,而PM-Tree方法中求解势能的步骤是主要耗时的部分[2]。所以求解泊松方程的速度是影响无碰撞引力N体数值模拟耗时的主要因素之一。
在具体的引力N体模拟中,N体粒子的数目不一定对应,往往不可能达到恒星或暗物质粒子的真实数量,数目N的设定,取决于模拟精度的需求以及计算能力。传统无碰撞引力N体数值模拟方法的计算速度适用于粒子数规模在106~1013的宇宙系统[1],模拟更大规模的宇宙系统的分布演化则需要计算速度更快的方法。深度神经网络在诸多解方程问题中都证明是有效的,并且还有速度快的优点,所以我们提出在传统无碰撞引力N体数值模拟方法PM-Tree中,使用深度神经网络代替快速傅里叶变换法计算主要耗时的求解势能部分。以粒子数规模为1013的系统为例,本文用深度神经网络的方法,单次势能求解的速度理论上能提高40倍左右,循环叠加后对整体模拟的加速较为可观,从各方面说明深度神经网络加速求解泊松方程的有效性,为后续加速无碰撞引力N体数值模拟的研究打下基础。因为深度神经网络具有可扩展的特点,所以在其他需要求解泊松方程的物理问题中,深度神经网络模型也能适用。
引力N体数值模拟方法主要有:(1)PP(Particle-to-Particle)方法,直接计算粒子间的牛顿引力,计算时间复杂度为O(N2)[3]。(2)当系统中粒子数量较多时,可以使用自1980年延用至今的Tree代码加快模拟速度[4-5]。Tree代码使用递归方式计算子树,省去了重复计算,将引力N体数值模拟的计算时间复杂度降低到O(NlogN),例如GASOLINE[6],iVINE[7]等。(3)PM(Particle Mesh)方法:首先使用CIC(Cloud-In-Cell)方法将粒子的位置信息转换为均匀网格的密度信息,然后通过快速傅里叶变换求解基于这些网格的泊松方程。该方法的计算时间复杂度为O(NlogN)[8],N代表网格单元数。(4)为了提高PM方法中网格内模拟粒子的精确率,在网格内使用Tree代码计算粒子间的相互作用,称为PM-Tree方法[9]。由于Tree代码每次在PM方法的一个小步骤内并行计算,而且一次Tree代码计算时间小于或等于PM方法中一个小步骤计算时间的二分之一[10],所以PM-Tree方法的计算时间复杂度和PM方法相同,为O(NlogN)。至今,PM-Tree方法为无碰撞引力N体数值模拟的主要方法之一,例如Gadget-2[11]。(5)近年来的N体程序(如Gadget-3, Gadget-4)[2]还实现了快速多极子方法(Fast Multipole Method, FMM)[12]。FMM可以将计算时间复杂度降到O(N),在相同精度下性能优于Tree方法,但算法更为复杂,特别是在动态步长、特殊边界条件、高效并行化等方面实现较为困难。
以上传统引力N体数值模拟方法的计算速度较慢,在超大规模粒子数量问题中难以适用,所以需要速度更快的方法。目前深度神经网络在很多领域的成果显著[13-14],并且神经网络也常用于解方程[15-16]。文[17]证明神经网络能解常微分方程和偏微分方程。引力N体数值模拟问题中的高维数据所需计算量巨大,而卷积神经网络的核心能力是从高维输入中提取多尺度特征[18-20],有效应对数值解偏微分方程中的维度诅咒问题[21]。所以我们采用深度卷积神经网络的方法,在无碰撞引力N体数值模拟方法PM-Tree中代替快速傅里叶变换法,更快求解势能。
1 相关工作近几年出现了一些使用深度神经网络求解偏微分方程的方法。由无碰撞玻尔兹曼方程的速度矩定义的Jeans方程,与流体力学中(无粘的)纳维-斯托克斯(Navier-Stokes)方程具有相同的形式,所以在这类流体领域解Navier-Stokes方程的相关研究结论也适用于引力N体数值模拟[22]。稳定流近似是一个Navier-Stokes流体问题, 是一种难以计算且非常耗时的迭代过程,文[23]使用卷积神经网络实现了快速准确的拟合。文[24]在随机多孔介质流动问题中使用卷积神经网络,仅用很少的数据就得到了满意的效果,优于蒙特卡洛法。文[25]证明在流场预测问题上使用卷积神经网络方法的有效性,而且速度比雷诺斯平均纳维-斯托克斯(Reynolds Averaged Navier-Stokes)法快。文[26]证明了神经网络可以简洁地求解具有不确定性的偏微分方程问题。文[27]在不适定(ill-posed)逆问题上使用深度神经网络迭代求解,速度提高十分显著。
不过这类用深度神经网络求解偏微分方程的方法是将求解算子参数化,并不直接,而且对于网格化尺寸不具有鲁棒性,但对于引力N体粒子数值模拟来说,要处理的问题是不停迭代的,需要更简单高效的求解方法。最近出现了一些针对特定问题直接求解偏微分方程的方法。文[28]在电磁领域求解二维图像形式的泊松方程,得到了很好的效果。文[29]提出了深度瑞兹(Deep Ritz)方法,在使用瑞兹方法求解偏微分方程过程中使用深度神经网络来寻找Ritz法的解,证明深度神经网络方法优于有限差分法。文[30]在无限维空间中证明使用深度神经网络参数化求解椭圆偏微分方程的有效性和收敛性。文[31]提出了一个艾克网络(Eiko Net),证明深度神经网络方法能够稳定求解艾克诺(Eikonal)方程,并能应用到多种领域,具有非常显著的计算速度优势。
2 本文工作及贡献我们结合目前深度学习速度快、有效解决高维度问题、能求解偏微分方程等特点,提出使用深度神经网络代替快速傅里叶变换法,求解无碰撞引力N体数值模拟方法PM-Tree中的势能。这种方法理论上可以更快地完成大规模的无碰撞引力N体数值模拟,并且可扩展性好,易于实现。我们搭建的深度神经网络模型,以及对应的训练和测试代码都在Github中开源,项目地址:https://github.com/hi76/Poisson-slover-based-on-Encoder-Decoder-Neural-Network。
3 方法N体数值模拟最早的直接求解法耗时巨大。平均场近似思想将难解的N体数值模拟转化为一个近似的统计问题,更易求解,但速度依然不快。后来陆续出现了一些优化的方法如PM方法、PM-Tree方法、FMM方法等,其中PM-Tree方法相比其他大多数N体数值模拟方法有速度快、精度高的优点,所以是目前主流的方法之一。在PM-Tree方法中主要耗时的步骤是求解势能。我们用深度神经网络模型代替快速傅里叶变换法,加速PM-Tree方法中势能的求解,以验证深度学习方法在加速无碰撞引力N体数值模拟中的可行性。
3.1 N体数值模拟物理学和天文学中,在一些物理作用力的影响下,对一个由粒子组成的系统的动力学模拟称为N体模拟。引力N体模拟主要是对N粒子引力相互作用方程求数值解。引力N体模拟在天体物理学中是一个常用的工具,从少体系统到宇宙大尺度结构,比如地球-月球-太阳系统到银河系中都有应用。N粒子引力相互作用方程为[32]
| $ \vec{F}_{i}=-\sum\limits_{j \neq i} G \frac{m_{i} m_{j}\left(\vec{r}_{i}-\vec{r}_{j}\right)}{\left|\vec{r}_{i}-\vec{r}_{j}\right|^{3}}-\vec{\nabla} \cdot \varPhi_{\mathrm{ext}}\left(\vec{r}_{i}\right), \quad i=1, \cdots, n, $ | (1) |
其中,G=6.673 00×10-11 m3·kg-1·s-2;Φext为外部势能。
N粒子引力相互作用系统定义了一个6N+1维的相空间,相空间中每个时刻每个粒子由N个位置和速度矢量确定。这个方程的解是相空间中的一个运动轨迹。直接求解这个方程十分耗时,所以需要简化的数值方法求解。
3.2 平均场法平均场法是出现较早的一种N体数值模拟方法。用统计方法描述引力N体问题时,系统分布f(x1, v1, …, xn, vn, t)描述了粒子的全部信息。当不考虑粒子间的关联,即认为f(2)(x1, v1, x2, v2, t)=f(1)(x1, v1, t)f(1)(x2, v2, t),平均场近似,即无碰撞N体系统。平均场近似中,粒子受到的作用力取决于分布函数,不必计算粒子两两之间的引力相互作用,这时我们可以用单粒子分布函数f(x, v, t)构造系统的平均场,即在d3xd3v的六维相空间中发现一个粒子的概率为f(x, v, t)d3xd3v。这个分布函数的演化可以由无碰撞玻尔兹曼方程描述[1]:
| $ \frac{D f}{D t}=\frac{\partial f}{\partial t}+\vec{v} \frac{\partial f}{\partial \vec{x}}-\frac{\partial \varPhi_{\mathrm{T}}}{\partial \vec{x}} \frac{\partial f}{\partial \vec{v}}=0. $ | (2) |
总潜在势能为外部势能和内部势能之和:
| $ \varPhi_{\mathrm{T}}=\varPhi_{\mathrm{ext}}(\vec{x}, t)+\varPhi(\vec{x}, t) . $ | (3) |
这个内部势能即所有N体粒子的引力势能构成的共同的自引力势,可以基于所有粒子的密度分布ρ(
| $\nabla^{2} \varPhi(\vec{x}, t)=4 {\rm{ \mathsf{π} }} G \rho(\vec{r}, t), $ | (4) |
其中,
PM-Tree方法也是一种N体数值模拟的方法。它在PM方法的网格内加入Tree代码,以实现更精细的模拟。因速度较快且精度较高,在最近的N体数值模拟应用中,常以PM-Tree方法为主进行模拟[2]。PM-Tree方法在每个时间步长(取决于模拟的时间区间以及模拟的精度要求)内模拟的基本步骤可以概括为[10]
(1) 首先确认Tree代码应用的网格以及当中的粒子,除此以外的粒子只由PM方法模拟计算;
(2) 运行PM方法的一半步骤;
(3) 计算每个Tree代码应用的网格对应的外部总势能——其余网格对它的势能和;
(4) 对这些应用的网格使用Tree代码同时计算,并将计算结果加入正在运行的PM方法步骤;
(5) 计算PM方法中的势能以及对应每个粒子的加速度;
(6) 将每个Tree整合到PM方法的最后步骤;
(7) 更新粒子的速度和位置信息,从步骤(1)开始循环计算。
因为在PM-Tree方法步骤中,Tree代码是和PM方法并行计算的,并且每次Tree代码计算所需时间不大于PM方法每次计算时间的一半,所以PM-Tree方法耗费的时间主要为PM步骤耗费的时间。在PM方法中,求解势能是主要耗时的计算步骤,而势能需要求解泊松方程得到。所以加速PM-Tree方法的关键在于加速求解泊松方程。PM-Tree方法的应用中,常用快速傅里叶变换法求解泊松方程[33]。本文用深度神经网络代替快速傅里叶变换法求解PM-Tree方法中的所有泊松方程,以加速PM-Tree方法,即加速N体数值模拟。
3.4 泊松方程数值求解传统求解泊松方程的方法有有限元法、有限差分法、有限体积法、快速傅里叶变换法等。利用计算机数值求解泊松方程,首先将泊松方程转换为代数方程,即差分方程。二维泊松方程的差分方程表示为
| $ \frac{\phi_{i+1, j}+\phi_{i-1, j}+\phi_{i, j+1}+\phi_{i, j-1}-4 \phi_{i, j}}{D T^{2}}=4 {\rm{ \mathsf{π} }} G \rho_{i, j}. $ | (5) |
分子是对ϕ做卷积,DT为离散化参数。(5)式在计算机中的操作可以简化表示为生成的势能ϕ和一个二阶差分算子▽的卷积:
| $ 4 {\rm{ \mathsf{π} }} G \rho=\frac{\left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array}\right]}{D T^{2}} \otimes \phi, $ | (6) |
其中,⊗为卷积操作符,卷积操作符的左边项是二阶差分算子▽。有限差分法求解泊松方程是将(5)式全部展开为一个有解的线性方程组,再用各类迭代法求解。有限差分法求解泊松方程的计算时间复杂度为O(N2)[34]。
快速傅里叶变换法是利用傅里叶变换将实数域中的卷积转换为复数域的乘法,将(6)式转换为一个复数域中易解的方程,求解后再做傅里叶逆变换,得到泊松方程的数值解[35]。快速傅里叶变换法的计算时间复杂度为O(NlogN)。因速度较快,在近来的引力N体数值模拟应用中,涉及求解泊松方程的步骤,主要用快速傅里叶变换法进行求解[2]。
三维泊松方程的二阶差分算子▽为
| $ \nabla=\frac{\left[\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right], \quad\left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -6 & 1 \\ 0 & 1 & 0 \end{array}\right], \quad\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right]\right]}{D T^{2}} . $ | (7) |
快速傅里叶变换求解三维泊松方程的原理和过程与二维相同,只是二阶差分算子▽不同,计算量更大。我们的目标是训练一个深度神经网络,以O(N)的计算时间复杂度,实现求解(6)式的反卷积过程,验证深度神经网络代替快速傅里叶变换法求解泊松方程,实现加速无碰撞引力N体数值模拟的可行性。因为我们关注的问题是深度神经网络是否可以实现求解(6)式的反卷积过程,所以选用消耗计算资源更少的二维泊松方程进行验证。
目前N体数值模拟的粒子数规模主要在106~1013之间。随着计算机计算能力的提升,能够模拟的粒子数规模以每年两倍左右的速度增长,符合摩尔定律。在无碰撞引力N体数值模拟中,影响模拟速度的主要因素为解泊松方程的速度。传统方法中常用的快速傅里叶变换求解的计算时间复杂度为O(NlogN)[1],而深度神经网络模型的计算时间复杂度为O(N),以粒子数规模1013为例,每一次泊松方程求解的速度理论上能提高40倍左右。在PM-Tree方法中,求解泊松方程的步骤需要循环执行很多次,所以循环叠加以后,计算时间复杂度O(N)的方法对无碰撞引力N体数值模拟的加速较为可观。而且随着将来模拟的粒子数规模不断增大,计算时间复杂度O(N)的方法能节省的时间也更加明显。
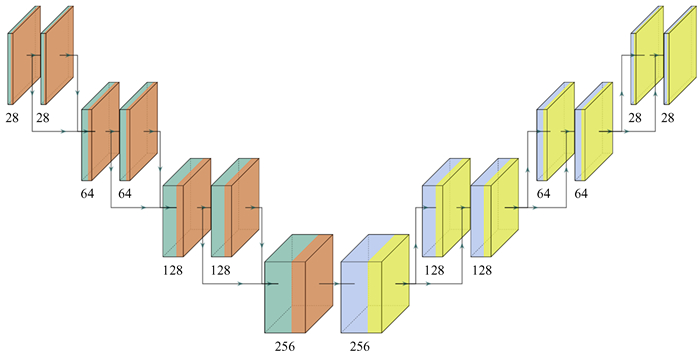
3.5 深度神经网络模型深度神经网络具有非常强的高维特征提取能力。在深度神经网络内部是一个非常高维的特征空间,所以一个复杂的深度神经网络模型,对于变化不是过于剧烈的输入数据具有鲁棒性。二维数据变为三维数据,相对于深度神经网络内部非常高维的特征空间,不是巨大的变化,而且即使数据复杂度变化较大,只要特征原理不变,深度神经网络也可以相应地增加模型的复杂度,维持原有的效果[18-20]。所以我们的主要目标是验证深度神经网络能够实现求解(6)式的反卷积过程。我们试验了数十种网络结构用于快速求解泊松方程,最终找到了目前效果最好的网络结构。因为在机器翻译中,将一种语义转化为另一种语义的端到端的神经网络多采用Encoder-Decoder结构[36],这与(4)式中的ϕ
|
| 图 1 神经网络模型结构。数字是卷积层通道数,左侧向下代表特征提取部分,右侧向上代表上采样部分。左侧绿色为卷积层,红色为激活函数;右侧蓝色为反卷积层,黄色为激活函数 Fig. 1 Neural network model Structure. The numbers are convolutional channels, with the left side down for feature extraction and the right side up for up-sampling. On the left side, green is the convolutional layer, red is the actication function, on the right side, blue is the convolutional transpose layer, yellow is the activation function |
我们的训练目标是最小化预测值和势能真值的平均平方误差
| $ \begin{gathered} E_{1}=\frac{1}{N} \sum(P-\varPhi)^{2} . \end{gathered} $ | (8) |
使用最大差值绝对值来评估误差
| $ E_{2}=\max |P-\varPhi| . $ | (9) |
卷积神经网络模型的计算时间复杂度为[38]
| $ \quad O\left(\sum\limits_{l=1}^{d} n_{l-1} s_{l}^{2} n_{l} m_{l}^{2}\right) . $ | (10) |
其中,l为卷积层索引;d为网络深度;nl为第l层的卷积核数量;nl-1为第l层的输入通道数;sl为卷积核尺寸;ml为输出特征图尺寸;N等于最后一层的输出特征图尺寸md2。由于神经网络模型中间参数量固定,且通常无碰撞引力N体数值模拟中的N
我们的目标是用深度神经网络代替快速傅里叶变换法,求解PM-Tree方法中的势能,以验证深度学习加速无碰撞引力N体数值模拟的可行性。其中关键任务是验证深度神经网络是否可以实现求解(6)式中的反卷积过程,所以需要训练得到一个可以作为泊松方程求解器的深度神经网络模型。本文使用随机生成的矩阵模拟网格化后需要预测的势能ϕ,即泊松方程的数值解,对生成图像做二阶差分得到模拟的输入分布ρ;建立一个深度神经网络模型,以多个卷积层提取特征,多个反卷积层表达特征输出预测势能;生成100万幅数据图,用平均平方误差对这个深度神经网络模型进行训练;最后对训练好的模型做精度测试,用于简单等时势问题的评估,并与快速傅里叶变换法做精度对比,与快速傅里叶变换法和有限差分法做时间对比,用多种网格化方式进行测试。
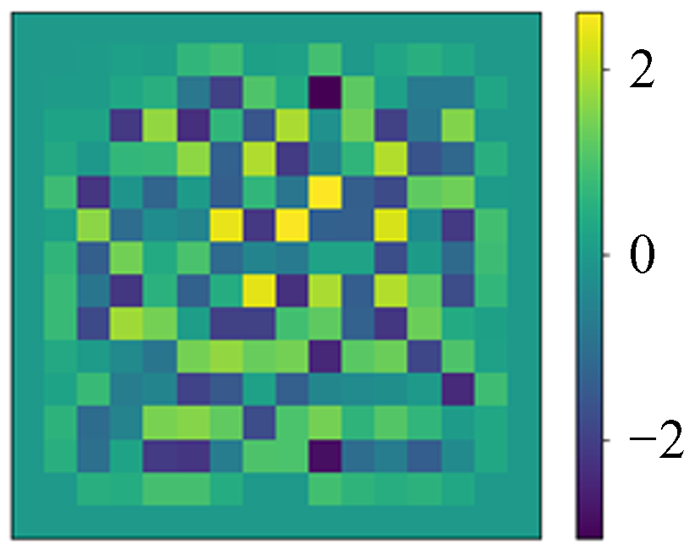
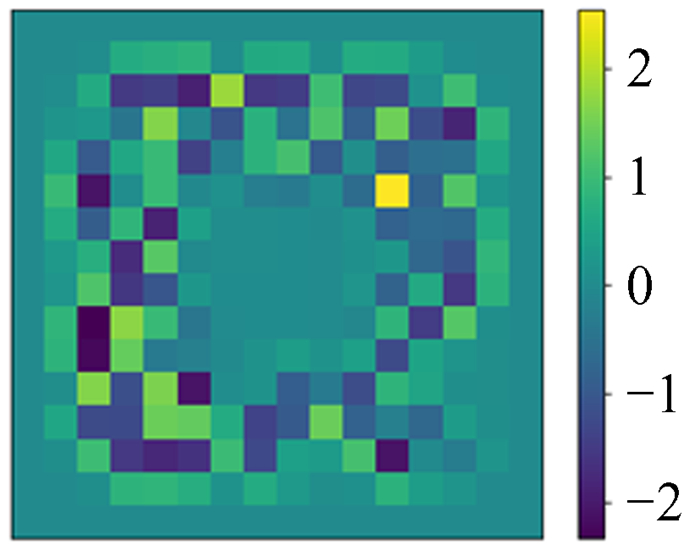
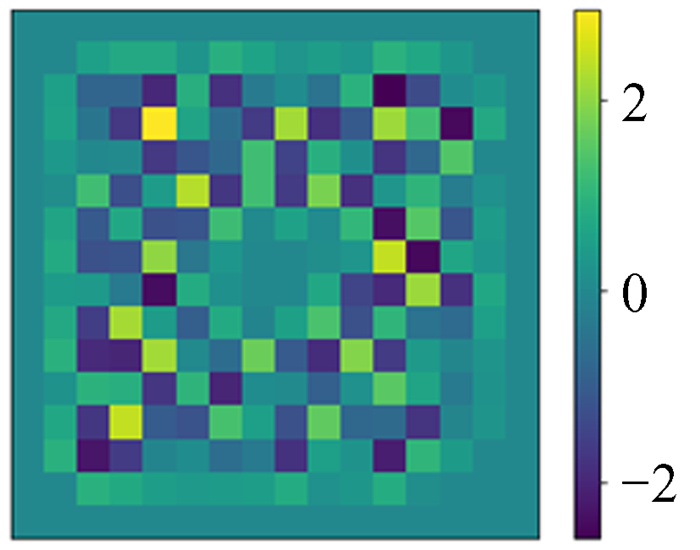
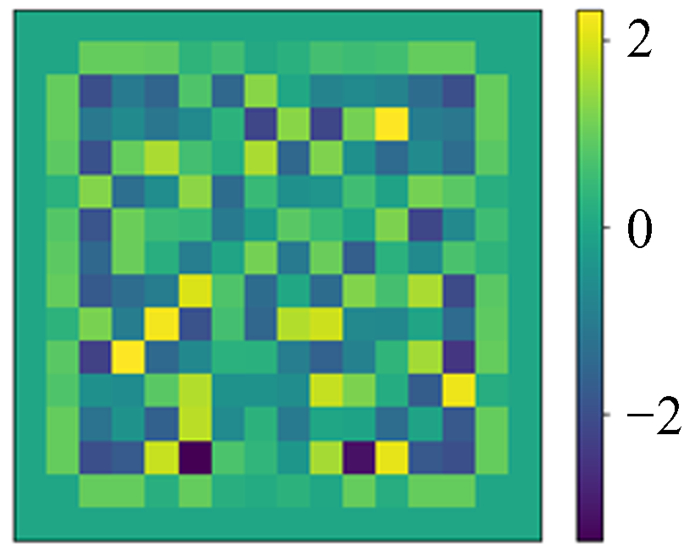
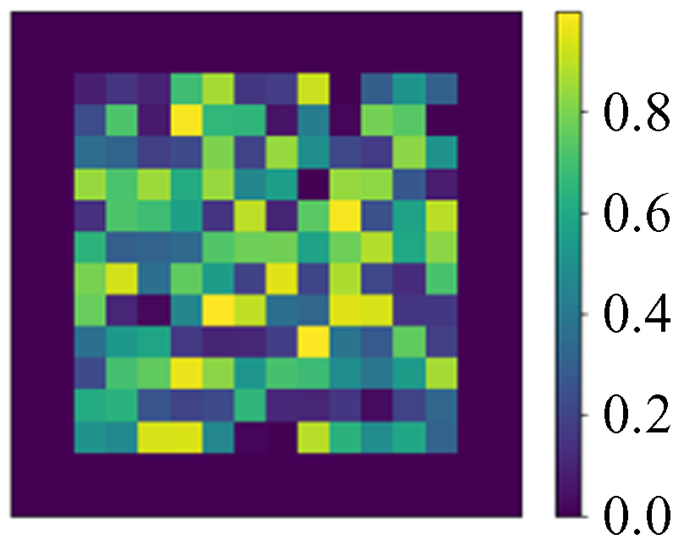
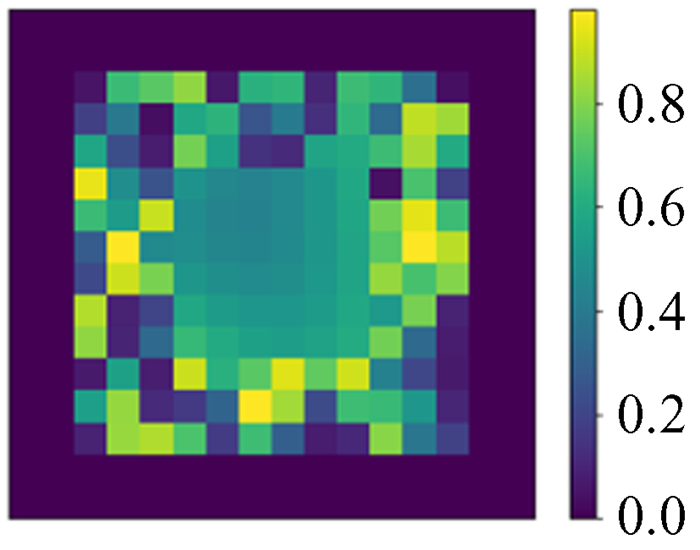
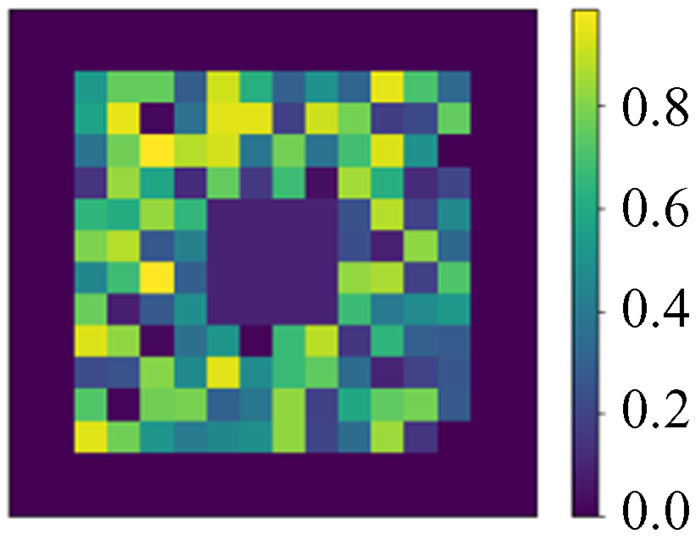
4.1 数据集我们生成100万幅图作为训练集,1万幅图作为测试集。这里我们假设将求解区域采样为N×N的网格,则使用的数据中模拟势能ϕ真值的构成为随机生成的N×N矩阵,然后将周围一圈值设置为0作为狄利克雷(Dirichlet)边界条件。采用Dirichlet边界条件的原因是在引力N体数值模拟中,通常我们关注的物质团周围很大区域是真空,可以近似为0,并且为了避免网络训练过于受到随机函数本身影响(随机函数得到的模式是不规律跳变值,相同的或平滑的情况很少),我们人为加入一些特殊模式作为数据增强,对中间部分区域做高斯平滑,将中间部分区域数值设置为0,将四角部分区域数值设置为0.99等。这些图像是模拟的泊松方程的解,也就是势能分布ϕ,是深度神经网络模型的预测目标,如图 2~图 5。
|
| 图 2 全随机 Fig. 2 Rand |
|
| 图 3 中间平滑 Fig. 3 Middle smooth |
|
| 图 4 中间置0 Fig. 4 Middle setting 0 |
|
| 图 5 四角置0.99 Fig. 5 Quadrant setting 0.99 |
需要模拟求解的分布ρ图,可以由以上模拟的势能ϕ通过(6)式得到,如图 6~图 9,这些分布ρ图就是深度神经网络模型的输入。
每次训练给深度神经网络模型输入ρ,用模型输出与ϕ的平均平方误差进行训练。因为数据是随机生成的,所以有不限数量的训练数据的优点。每次生成100万对数据用于训练。
4.2 训练参数我们在Pytorch中实现深度神经网络模型。每次训练使用100万对数据,批大小设置为100,优化器选用Adam[39],学习率从0.01视情况调整到0.000 001。每组数据训练100次,训练使用的图形处理器是Tesla P100。
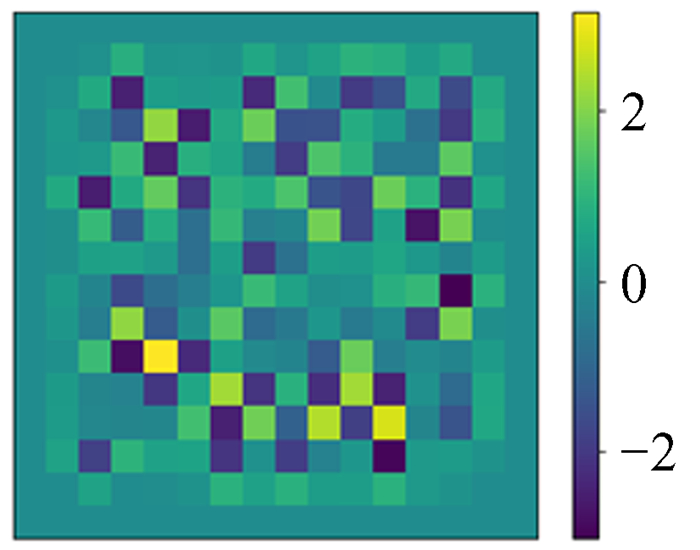
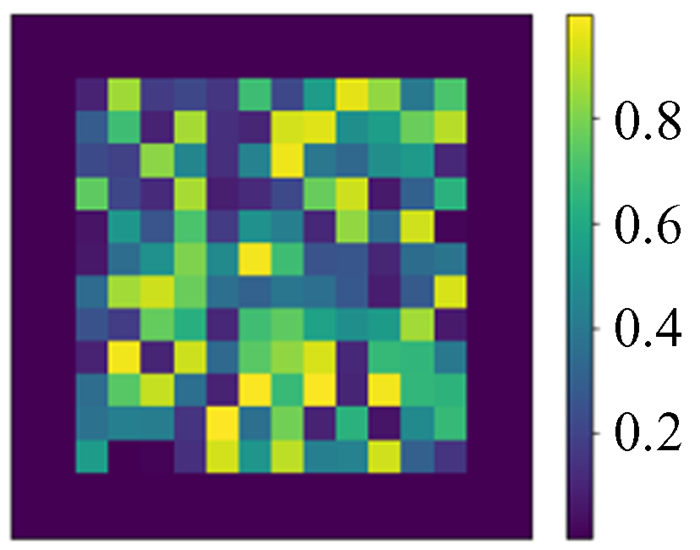
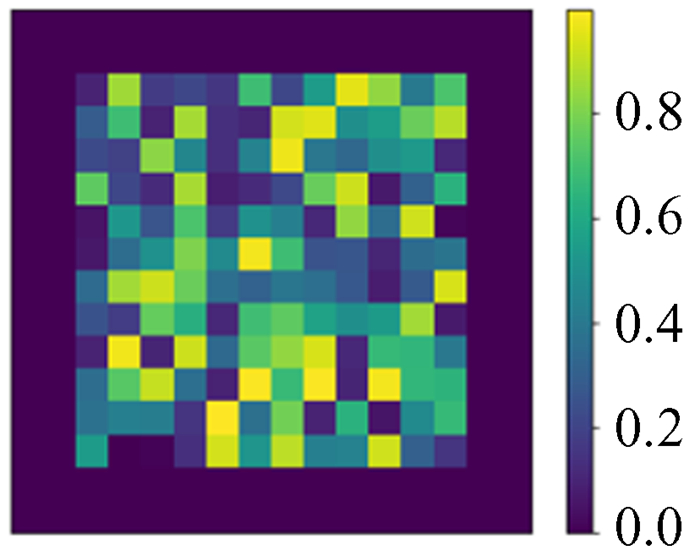
5 训练成果及测试 5.1 训练成果输入模拟分布函数ρ图,通过神经网络模型得到预测图,与模拟势能ϕ真值图比较并作差,训练成果如图 10~图 13。
|
| 图 10 模拟ρ Fig. 10 Simulation ρ |
|
| 图 11 模拟ϕ Fig. 11 Simulation ϕ |
|
| 图 12 预测值 Fig. 12 Prediction |
|
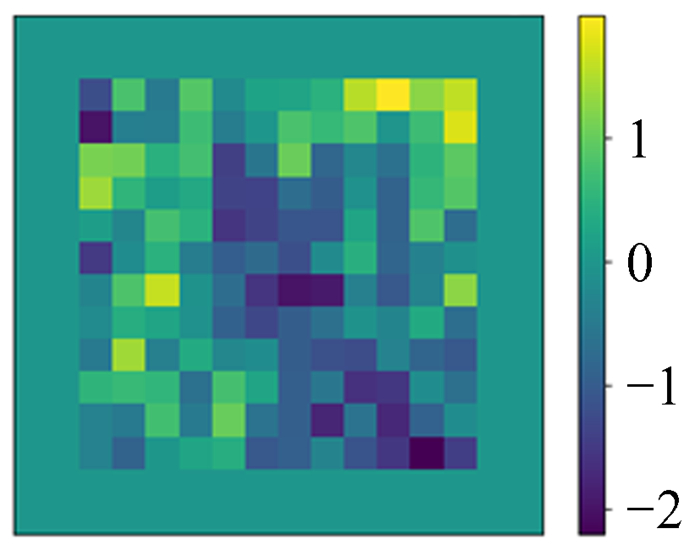
| 图 13 预测值与模拟ϕ的相对误差 Fig. 13 Relative error between prediction and simulation ϕ |
由图 10~图 13可以看出,深度神经网络模型的预测图和模拟势能ϕ真值图肉眼几乎看不出区别,图像特征基本吻合,它们的相对误差最大为2×10-4,精度达到泊松方程的求解目标。
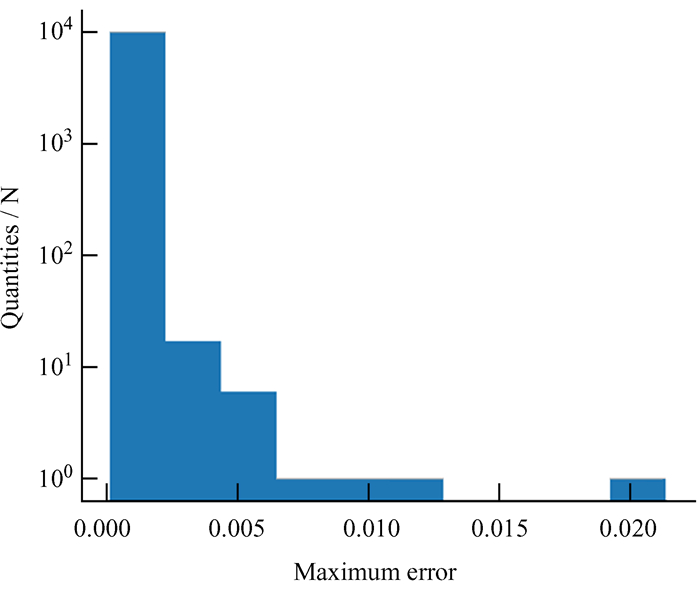
5.2 测试结果我们使用1万对新生成数据用于测试,结果如图 14,统计得到不同最大误差精度的准确率如表 1。
|
| 图 14 10 000组数据测试结果 Fig. 14 Test results for 10 000 sets of data |
| Maximum error | Accuracy/% |
| < 0.000 5 | 94 |
| < 0.001 | 99 |
| < 0.005 | 99.9 |
为了验证模型的普适性,我们用16×16数据训练的神经网络模型用于渐增网格化尺寸(16×16-1 024×1 024)的图像进行测试,如图 15~图 16。
|
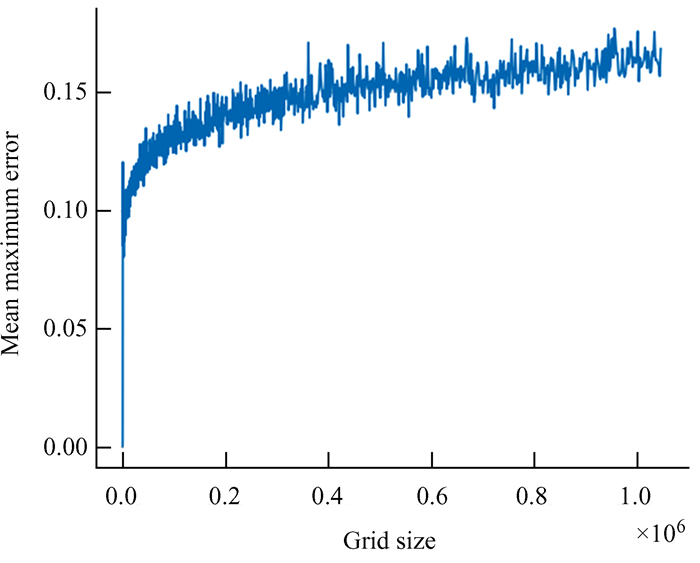
| 图 15 平均最大误差趋势图 Fig. 15 Maximum error trend graph |
|
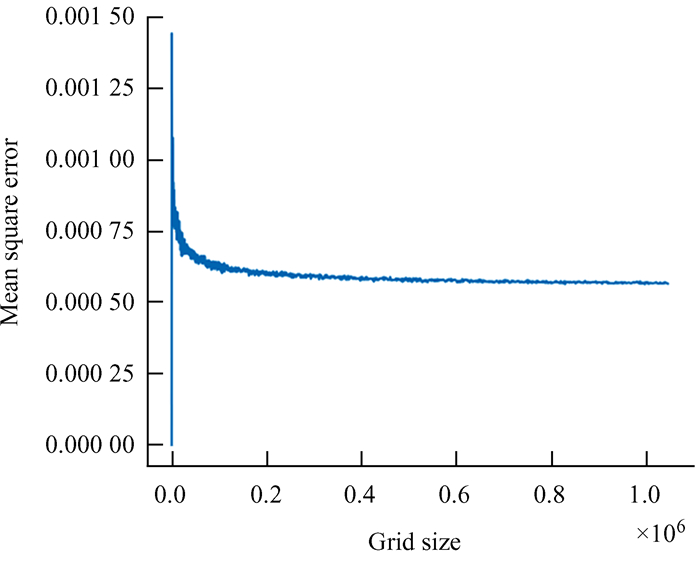
| 图 16 平均平方误差趋势图 Fig. 16 Mean squared error trend graph |
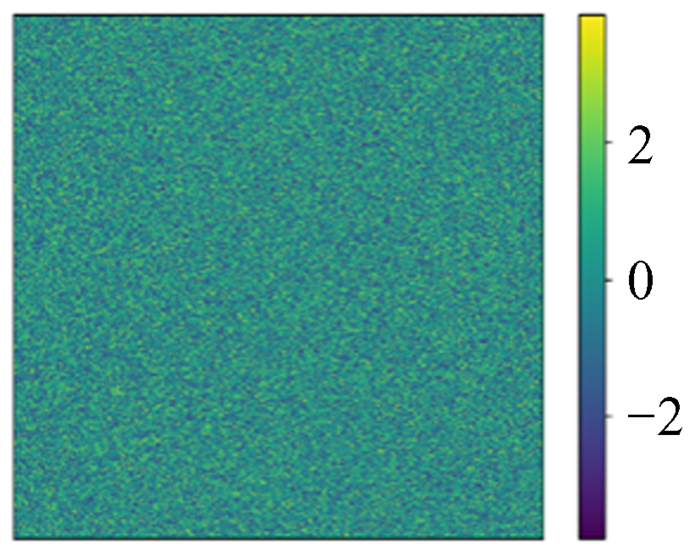
由图 15~图 16可以看出,最大误差趋势渐平,不随网格化尺寸增大而线性增大。从平均平方误差图也能看出,随着网格化尺寸增大,平均以后的平方误差反而减小,当网格化尺寸足够大以后,误差基本不变。其中两组模拟数据(256×256, 1 024×1 024)如图 17~图 24。
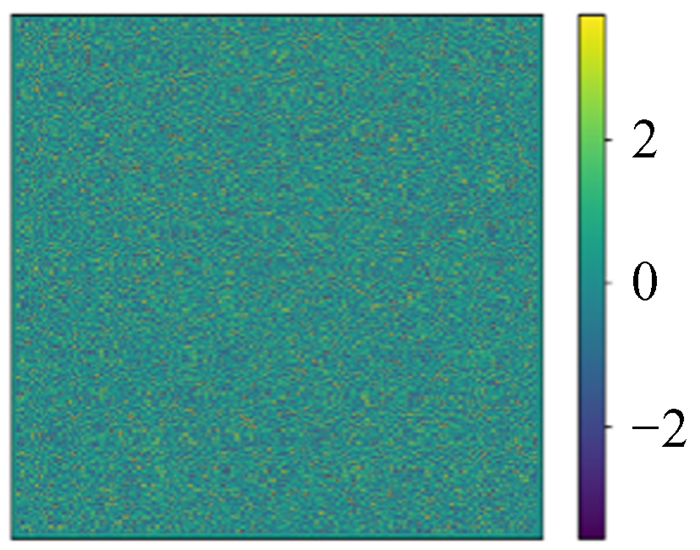
|
| 图 17 模拟256×256 ρ Fig. 17 Simulation 256×256 ρ |
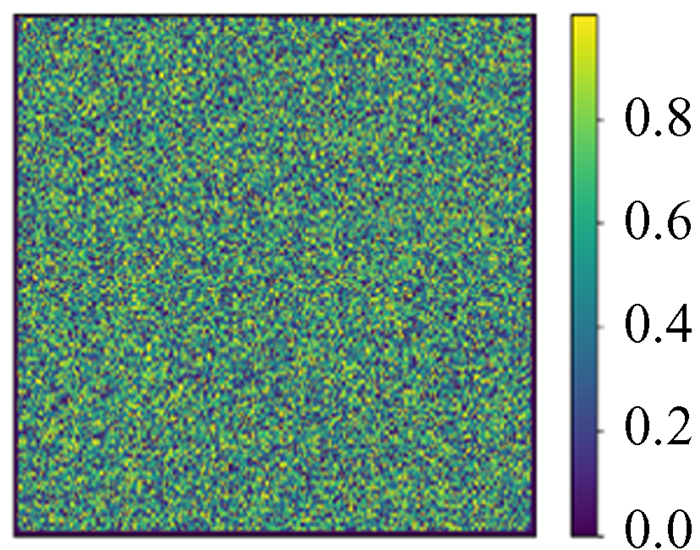
|
| 图 18 模拟256×256 ϕ Fig. 18 Simulation 256×256 ϕ |
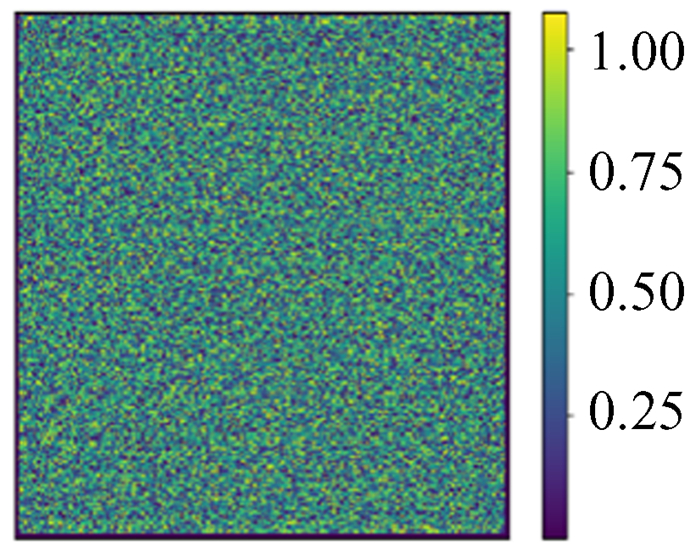
|
| 图 19 256×256预测值 Fig. 19 256×256 Prediction |
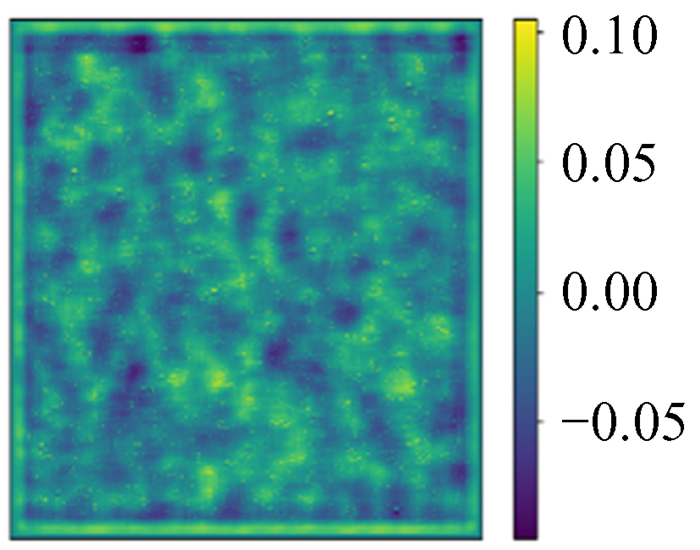
|
| 图 20 预测值与模拟ϕ的相对误差 Fig. 20 Relative error between prediction and simulation ϕ |
|
| 图 21 模拟1 024×1 024 ρ Fig. 21 Simulation 1 024×1 024 ρ |
|
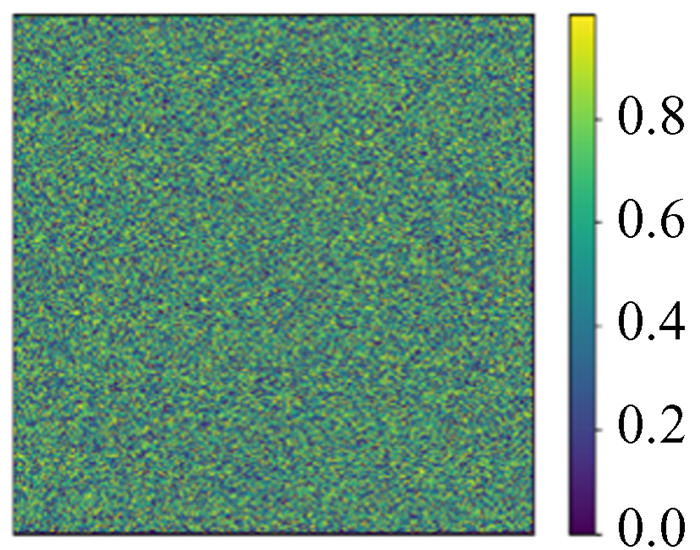
| 图 22 模拟1 024×1 024 ϕ Fig. 22 Simulation 1 024×1 024 ϕ |
|
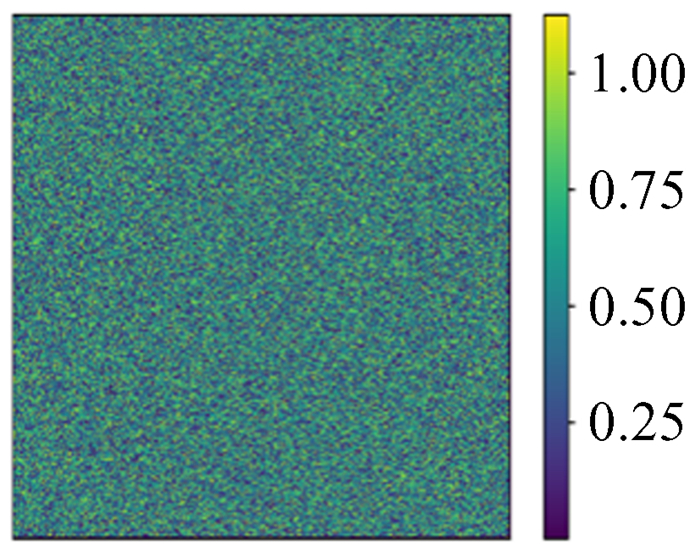
| 图 23 1 024×1 024预测值 Fig. 23 1 024×1 024 Prediction |
|
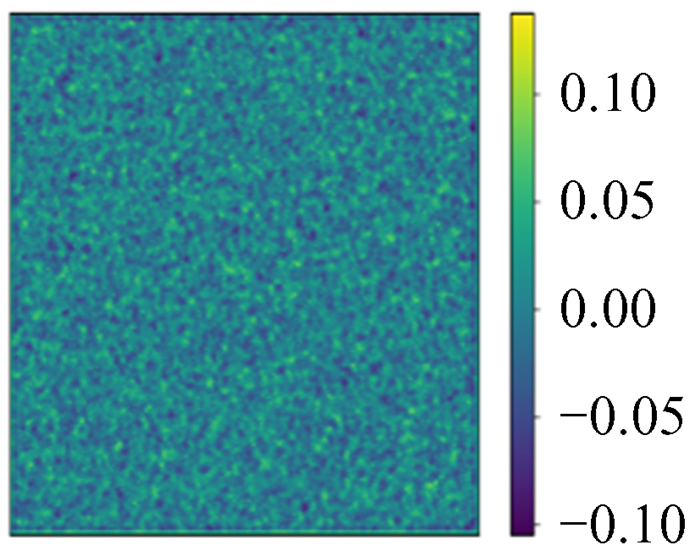
| 图 24 预测值与模拟ϕ的相对误差 Fig. 24 Relative error between prediction and simulation ϕ |
由图 17~图 24可以看出,用图 10这类16×16尺寸数据训练的网络,在更大尺度上依然具有普适性。经过各种尺度图像的对比分析,最大误差变大的原因是更大尺寸的数据包含的局部特殊模式更多。这些特殊模式是在测试集数据测试时出现的那些误差较大的点。但总体可以说明,小尺寸数据训练的模型可以用于大尺寸数据。这意味着模型训练的时间成本可以非常低。
5.4 等时势问题测试我们将训练好的模型用于一个实际的物理问题——等时势问题。按
| $ \begin{gathered} \rho(r)=M\left[\frac{3 a^{2}(b+a)-r^{2}(b+3 a)}{4 {\rm{ \mathsf{π} }} a^{3}(b+a)^{3}}\right] , \end{gathered} $ | (11) |
| $ \phi(r)=-\frac{G M}{b+\sqrt{b^{2}+r^{2}}} $ | (12) |
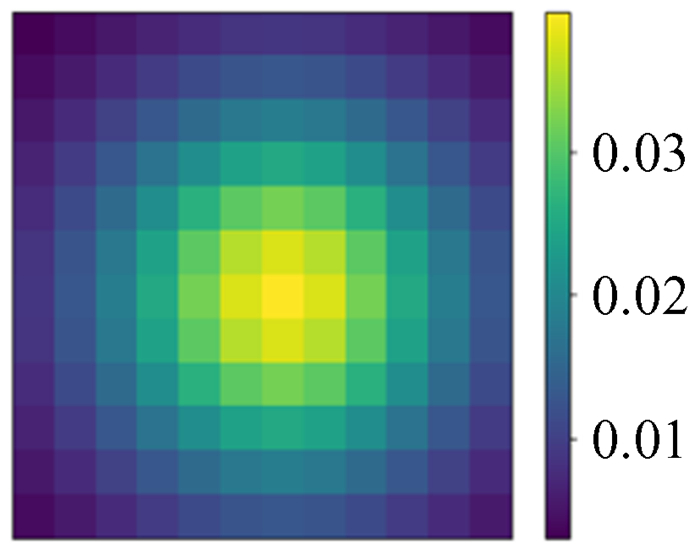
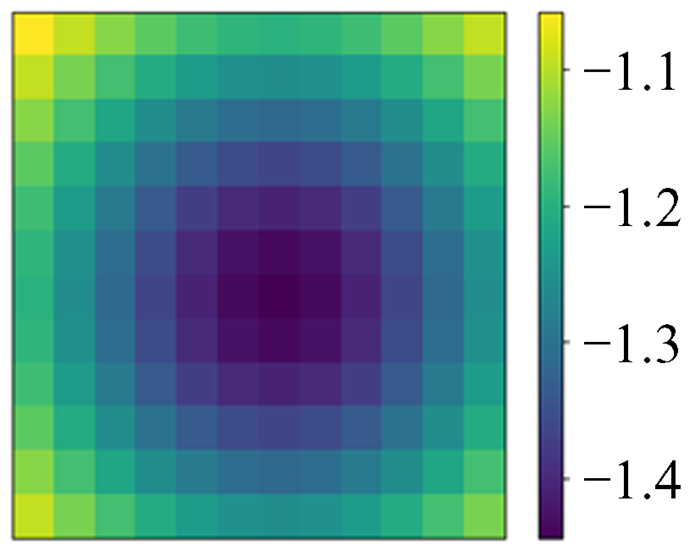
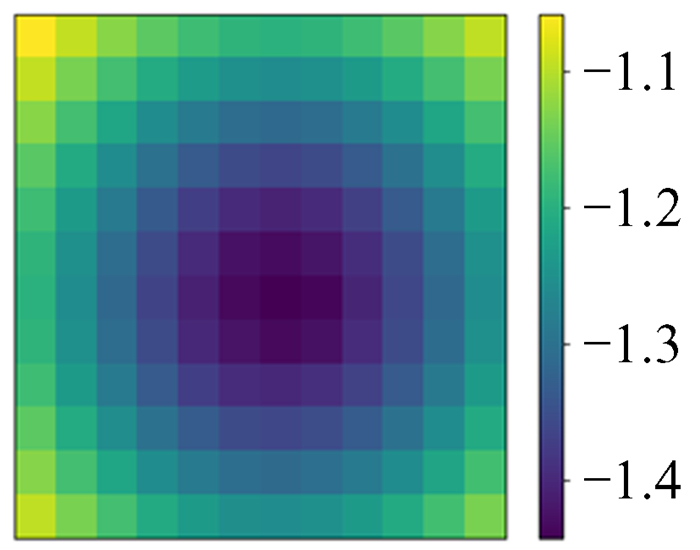
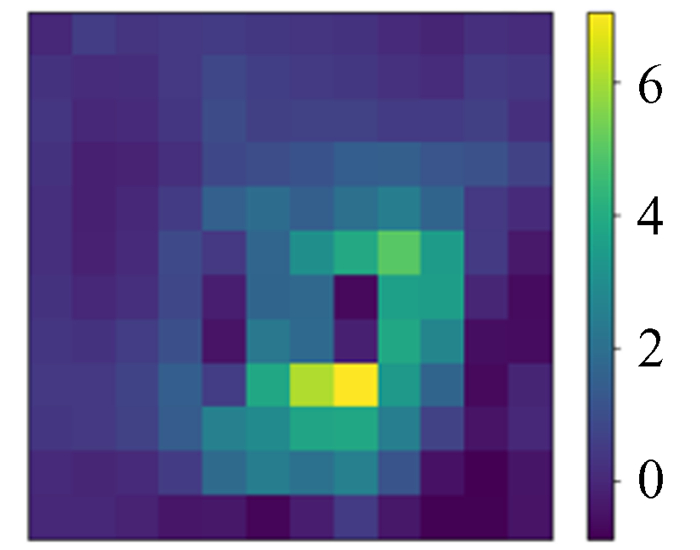
生成等时势问题的ϕ和ρ图像。将ρ输入训练好的深度神经网络模型进行测试,得到预测值,将预测值与模拟ϕ作差对比,如图 25~图 28。由图 25~图 28可以看出,在实际的物理问题中,深度神经网络模型依然表现良好。
|
| 图 25 模拟ρ Fig. 25 Simulation ρ |
|
| 图 26 模拟ϕ Fig. 26 Simulation ϕ |
|
| 图 27 网络预测值 Fig. 27 Network Prediction |
|
| 图 28 网络预测值与模拟ϕ的误差 Fig. 28 Error between Network prediction and simulation ϕ |
我们将同样的数据用于快速傅里叶变换法求解,以做精度对比。如图 29~图 30。

|
| 图 29 快速傅里叶变换求解值 Fig. 29 FFT Prediction |
|
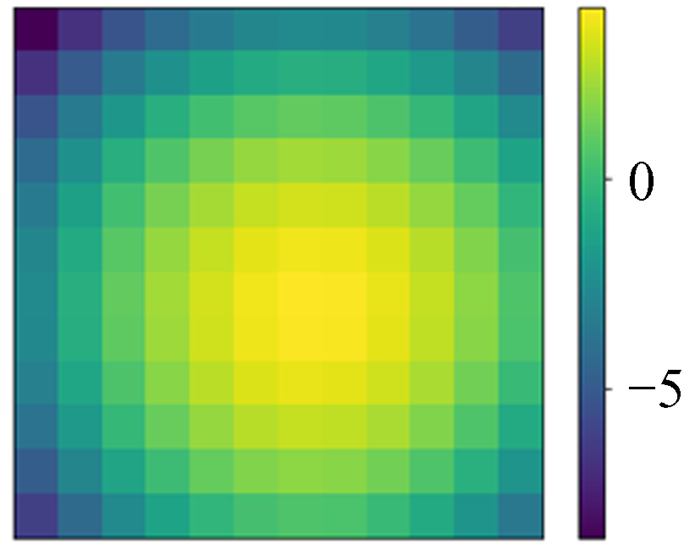
| 图 30 快速傅里叶变换求解值与模拟ϕ的误差 Fig. 30 Error between FFT prediction and simulation ϕ |
图 28和图 30对比可以看出,在同样采样率的情况下,深度神经网络模型的精度高于快速傅里叶变换法,满足精度要求。
5.5 与快速傅里叶变换法及有限差分法的计算时间对比实验生成网格化尺寸逐渐增长的数据,分别对比测试训练好的深度神经网络模型和快速傅里叶变换法以及有限差分法的计算时间。测试结果如图 31~图 32。
|
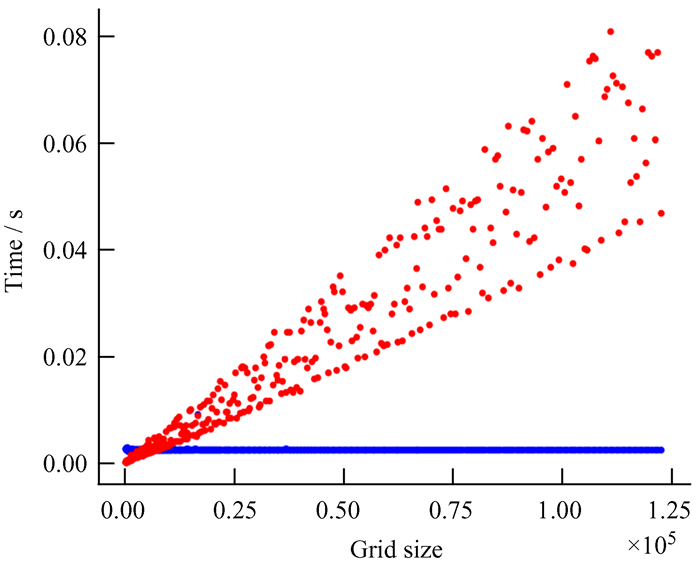
| 图 31 神经网络模型和快速傅里叶变换法计算时间对比。蓝色代表神经网络模型,红色代表快速傅里叶变换法 Fig. 31 Comparison of neural network model and fast Fourier transform computation times. Blue represents the neural network model and red represents the fast Fourier transform |
|
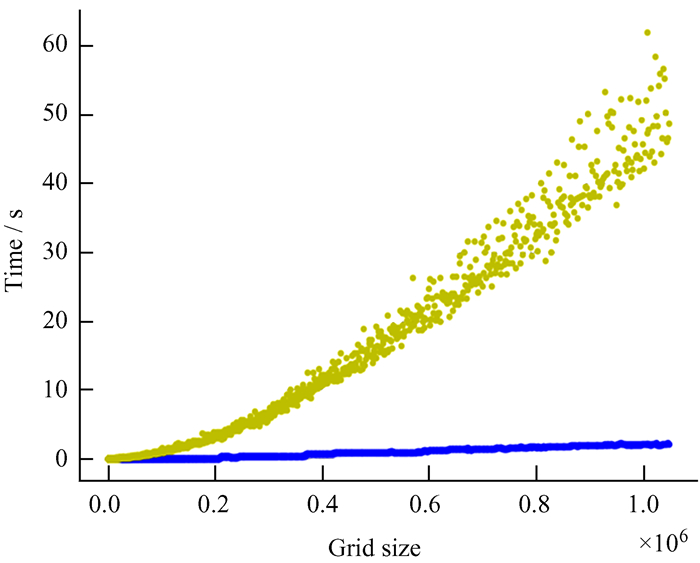
| 图 32 神经网络模型和有限差分法计算时间对比。蓝色代表神经网络模型,黄色代表有限差分法 Fig. 32 Comparison between the neural network model and the finite difference method computation times. Blue represents the neural network model, yellow represents the finite difference method |
实验结果可以看出,深度神经网络方法求解泊松方程,随着数据网格化尺寸增大,计算速度快于快速傅里叶变换法以及有限差分法。这归功于两点:(1)深度神经网络可以利用图形处理器进行快速计算;(2)从实验结果图可以看出,深度神经网络的计算时间趋势为线性增长,而快速傅里叶变换法为NlogN倍增长,有限差分法更是N2倍增长。这个结论与前文卷积神经网络计算时间复杂度理论分析相互印证。
5.6 失败神经网络模型结构概述这里描述一些试验结果差的网络结构,数据生成方式和上述相同。第1种是纯卷积网络结构,通道数为1-128-256-512-256-128,最后平均平方误差收敛到0.000 3,误差较大。在第1种网络结构的中间每个卷积层后插入归一化层,效果变差,平均平方误差只能收敛到0.14。加入一种网络基础模块,对每次输入进行一次卷积,再将卷积后的输出与输入叠加作为下一层的输入,下一层再通过卷积将维度变回初始输入的维度,效果也不如纯卷积网络,平均平方误差只能收敛到0.005。在纯卷积网络末端加入两层全连接层,不仅参数量骤增,平均平方误差也仅能达到0.01。将全连接层加到前端以及后端,平均平方误差能到0.000 8,但参数量大,训练很慢,且效果不如简单的纯卷积网络。将纯卷积网络中间两层的步长改为2,提取更精简的特征,并在后端的两层将卷积改为反卷积进行上采样,此时平均平方误差降到10-6,比纯卷积网络效果更好,但依然达不到精度要求。采用一次卷积一次反卷积迭代的网络结构,平均平方误差只能到0.3。在纯卷积网络结构上,加入模仿ResNet的网络基础模块,对某次输入进行一次卷积,然后将输入和输出相加作为下一层的输入,一次卷积,一次残差模块,连续进行6次,平均平方误差能达到10-5。基于以上网络结构的试验,最后综合各种结构的优劣势,我们设计了最终的深度神经网络模型结构。
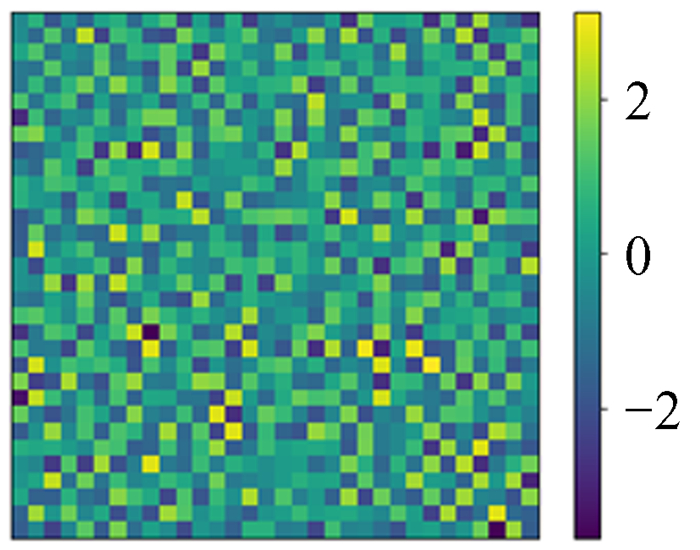
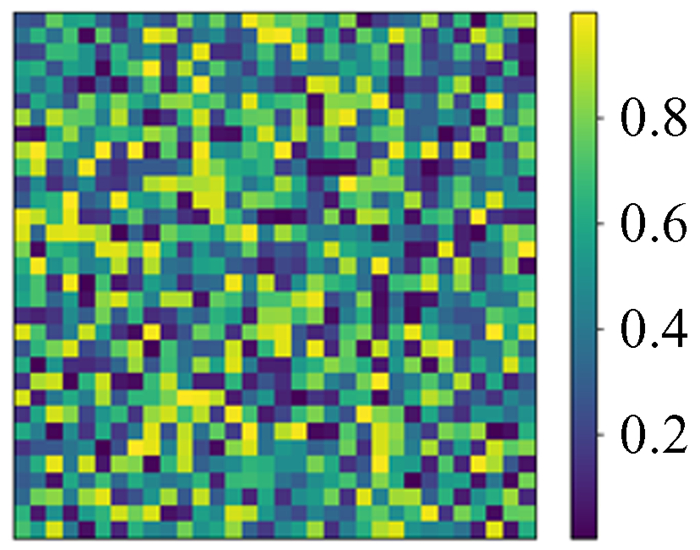
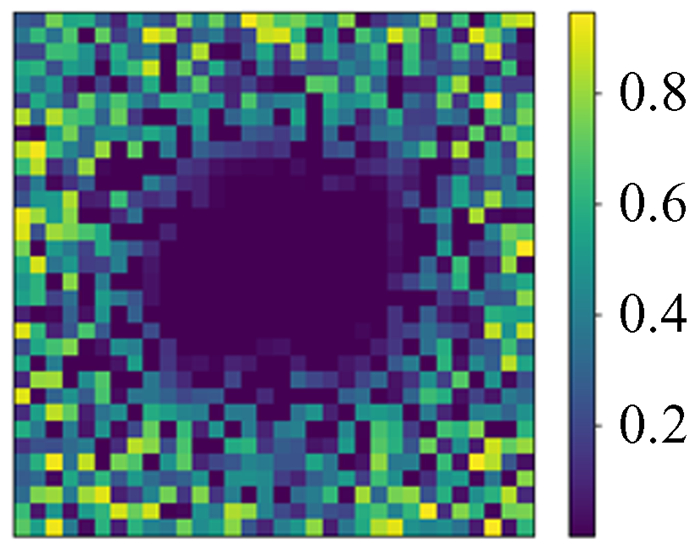
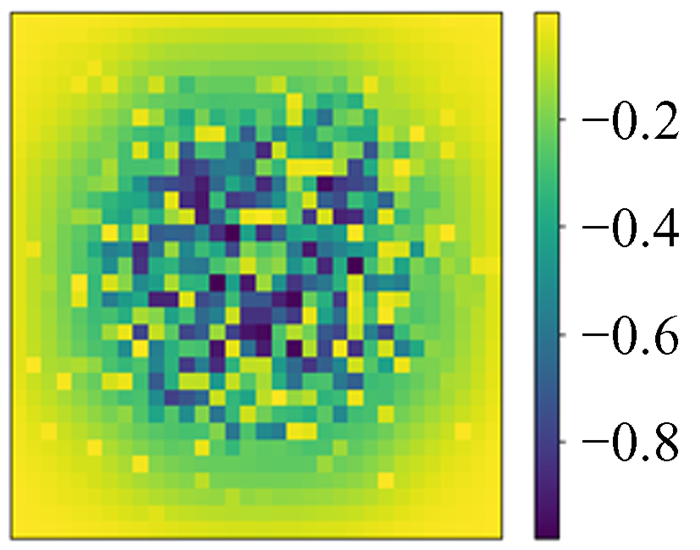
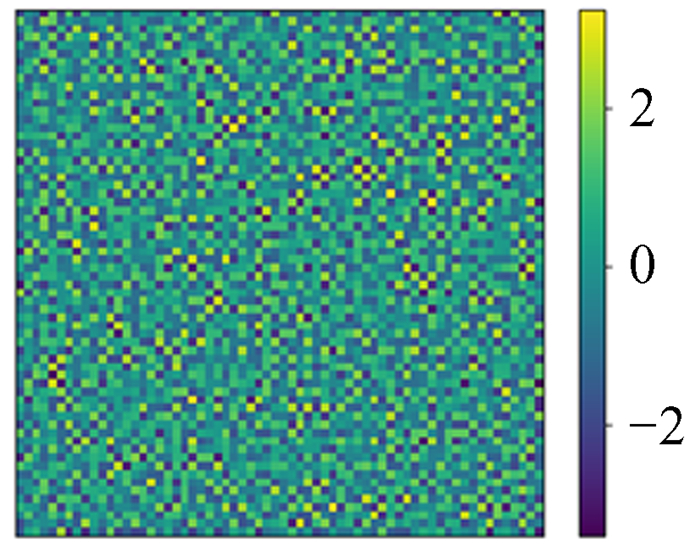
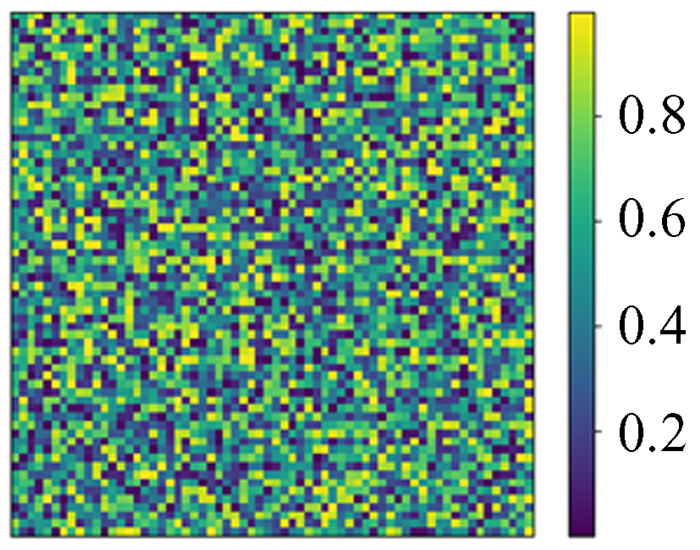
5.7 有趣实验现象我们所给的数据都设置了Dirichlet边界条件的数据,尝试不设置边界条件会发生什么。用神经网络模型对不设置边界的16×16数据进行训练,训练过程和结果的精度与给定边界条件时的情况相似。在同网格化尺寸下训练结果的相对误差精度也可以达到10-4,但将训练的神经网络模型用于更大网格化尺寸的数据上时,就发生了有趣的现象,它只能预测到边缘16宽度的范围,中间部分几乎为0,如图 33~图 40。
|
| 图 33 模拟32×32 ρ Fig. 33 Simulation 32×32 ρ |
|
| 图 34 模拟32×32 ϕ Fig. 34 Simulation 32×32 ϕ |
|
| 图 35 32×32预测值 Fig. 35 32×32 prediction |
|
| 图 36 预测值与模拟ϕ的相对误差 Fig. 36 Relative error between prediction and simulation ϕ |
|
| 图 37 模拟64×64 ρ Fig. 37 Simulation 64×64 ρ |
|
| 图 38 模拟64×64 ϕ Fig. 38 Simulation 64×64 ϕ |
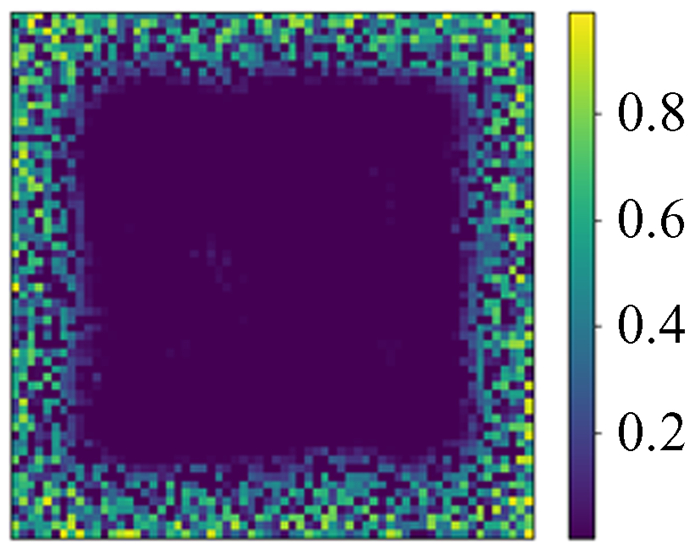
|
| 图 39 64×64预测值 Fig. 39 64×64 prediction |
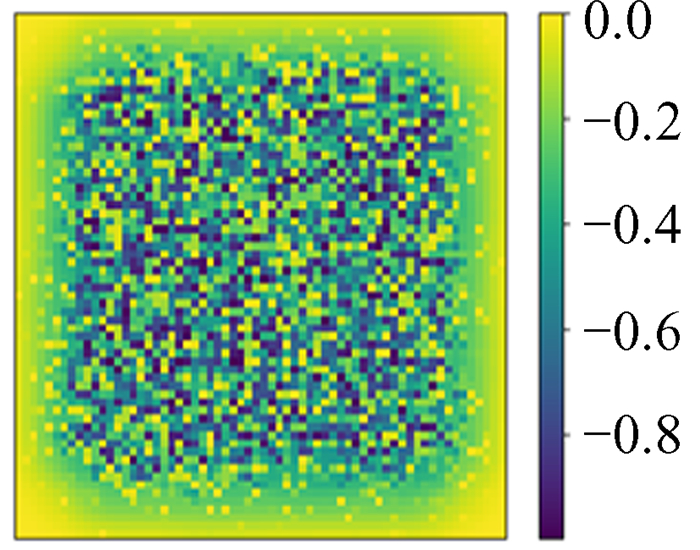
|
| 图 40 预测值与模拟ϕ的相对误差 Fig. 40 Relative error between prediction and simulation ϕ |
结合神经网络模型具有不同网格化数据的普适性分析,这样的现象可能是因为训练好的神经网络模型是局部迭代操作,同时又是从边界开始向内求解泊松方程造成的。
5.8 实验总结综合以上实验结果可以得出:深度神经网络模型具有快速求解PM-Tree方法中势能的能力, 精度不低于快速傅里叶变换法,速度优于快速傅里叶变换法和有限差分法,特别是随着无碰撞引力N体数值模拟的粒子数规模增加,深度神经网络模型的速度优势更加明显;在未经训练的更大网格化尺寸数据上也能使用,具有可扩展性。所以深度学习的方法在加速无碰撞引力N体数值模拟中是可行的。
6 结论本文在神经网络解各类方程的研究和几种无碰撞引力N体数值模拟方法的基础上,提出了用一个辅以残差局部结构的Encoder-Decoder深度神经网络模型求解PM-Tree方法中的势能,代替常用的快速傅里叶变换求解;验证了深度神经网络模型可以快速求解泊松方程,理论上深度神经网络的计算时间复杂度为O(N);验证了深度神经网络模型计算耗时低于快速傅里叶变换法以及有限差分法;验证了在相同离散化采样率的情况下,深度神经网络模型求解精度不低于快速傅里叶变换法;验证了深度神经网络具有可扩展性,在小网格化尺寸数据集上训练的模型可以应用于大网格化尺寸数据集。并且深度神经网络模型可以更好地利用图形处理器的计算资源进行并行处理,在粒子数规模较大时,速度优势更加明显。综合以上验证结果,我们提出使用深度神经网络代替快速傅里叶变换法求解PM-Tree方法中的势能,可以加速PM-Tree方法中主要的耗时步骤,即可以加速无碰撞引力N体数值模拟,验证了深度学习方法在无碰撞引力N体数值模拟中的可行性,为将来实际应用大规模无碰撞引力N体数值模拟打下基础。
7 未来与展望未来工作主要有3方面。(1)拓展解泊松方程由二维到三维(只需简单地将现有神经网络模型中的二维卷积改为三维卷积即可);(2)加入迭代求解过程,实现时变的模拟;(3)将模型嵌入无碰撞引力N体数值模拟的PM-Tree方法中实际应用。
致谢: 感谢刘冬明、翟顺诚在工作中提出的意见;感谢顾建宇对文章部分内容的修正。
| [1] | DEHNEN W, READ J I. N-body simulations of gravitational dynamics[J]. The European Physical Journal Plus, 2011, 126(5): 55. DOI: 10.1140/epjp/i2011-11055-3 |
| [2] | SPRINGEL V, PAKMOR R, ZIER O, et al. Simulating cosmic structure formation with the GADGET-4 code[J]. Monthly Notices of the Royal Astronomical Society, 2021, 506(2): 2871–2949. DOI: 10.1093/mnras/stab1855 |
| [3] | AARSETH S J. Gravitational N-body simulations: tools and algorithms[M]. New York: Cambridge University Press, 2003. |
| [4] | BARNES J, HUT P. A hierarchical O (N logN) force-calculation algorithm[J]. Nature, 1986, 324(6096): 446–449. DOI: 10.1038/324446a0 |
| [5] | APPEL A W. An effificient program for many-body simulation[J]. SIAM Journal on Scientifific and Statistical Computing, 1985, 6(1): 85–103. DOI: 10.1137/0906008 |
| [6] | WADSLEY J W, STADEL J, QUINN T. Gasoline: a flexible, parallel implementation of treesph[J]. New Astronomy, 2004, 9(2): 137–158. DOI: 10.1016/j.newast.2003.08.004 |
| [7] | GRITSCHNEDER M, NAAB T, BURKERT A, et al. iVINE-ionization in the parallel tree/sph code VINE: first results on the observed age-spread around O-stars[J]. Monthly Notices of the Royal Astronomical Society, 2009, 393(1): 21–31. DOI: 10.1111/j.1365-2966.2008.14185.x |
| [8] | EASTWOOD J W, HOCKNEY R W. Computer simulation using particles[M]. New York: McGraw Hill, 1981. |
| [9] | SPRINGEL V, WHITES D M, JENKINS A, et al. Simulations of the formation, evolution and clustering of galaxies and quasars[J]. Nature, 2005, 435(7042): 629–636. DOI: 10.1038/nature03597 |
| [10] | BODE P, OSTRIKER J P. Tree particle-mesh: an adaptive, effificient, and parallel code for collisionless cosmological simulation[J]. The Astrophysical Journal Supplement Series, 2003, 145(1): 1. DOI: 10.1086/345538 |
| [11] | SPRINGEL V. The cosmological simulation code gadget-2[J]. Monthly Notices of the Royal Astronomical Society, 2005, 364(4): 1105–1134. DOI: 10.1111/j.1365-2966.2005.09655.x |
| [12] | GREENGARD L, ROKHLIN V. A fast algorithm for particle simulations[J]. Journal of Computational Physics, 1987, 73(2): 325–348. DOI: 10.1016/0021-9991(87)90140-9 |
| [13] | SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural Networks, 2015, 61: 85–117. DOI: 10.1016/j.neunet.2014.09.003 |
| [14] | BENGIO Y. Learning deep architectures for AI[M]//Foundations and Trends in Machine Learning. Boston: Now Publishers Incorporation, 2009. |
| [15] | HORNIK K, STINCHCOMBE M, WHITE H, et al. Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2(5): 359–366. DOI: 10.1016/0893-6080(89)90020-8 |
| [16] | SPECHT D F. A general regression neural network[J]. IEEE Transactions on Neural Networks, 1991, 2(6): 568–576. DOI: 10.1109/72.97934 |
| [17] | LAGARIS I E, LIKAS A, FOTIADIS D I. Artifificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5): 987–1000. DOI: 10.1109/72.712178 |
| [18] | KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classifification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84–90. DOI: 10.1145/3065386 |
| [19] | ZUO Z, SHUAI B, WANG G, et al. Convolutional recurrent neural networks: learning spatial dependencies for image representation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. 2015: 18-26. |
| [20] | LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436–444. DOI: 10.1038/nature14539 |
| [21] | HAN J Q, JENTZEN A, E W N. Solving high-dimensional partial differential equations using deep learning[J]. Proceedings of the National Academy of Sciences, 2018, 115(34): 8505–8510. DOI: 10.1073/pnas.1718942115 |
| [22] | BINNEY J, TREMAINE S. Galactic dynamics[M]. Princeton: Princeton University Press, 1987. |
| [23] | GUO X X, LI W, IORIO F. Convolutional neural networks for steady flow approximation[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2016: 481-490. |
| [24] | ZHU Y H, ZABARAS N. Bayesian deep convolutional encoder-decoder networks for surrogate modeling and uncertainty quantifification[J]. Journal of Computational Physics, 2018, 366: 415–447. DOI: 10.1016/j.jcp.2018.04.018 |
| [25] | BHATNAGAR S, AFSHAR Y, PAN S W, et al. Prediction of aerodynamic flow fields using convolutional neural networks[J]. Computational Mechanics, 2019, 64(2): 525–545. DOI: 10.1007/s00466-019-01740-0 |
| [26] | KHOO Y, LU J F, YING L X. Solving parametric PDE problems with artificial neural networks[J]. European Journal of Applied Mathematics, 2021, 32(3): 421–435. DOI: 10.1017/S0956792520000182 |
| [27] | ADLER J, ÖKTEM O. Solving ill-posed inverse problems using iterative deep neural networks[J]. Inverse Problems, 2017, 33(12): 124007. DOI: 10.1088/1361-6420/aa9581 |
| [28] | TANG W, SHAN T, DANG X W, et al. Study on a poisson's equation solver based on deep learning technique[C]//Proceedings of the 2017 IEEE Electrical Design of Advanced Packaging and Systems Symposium (EDAPS). 2017: 1-3. |
| [29] | E W N, YU B. The Deep Ritz Method: a deep learning-based numerical algorithm for solving variational problems[J]. Communications in Mathematics and Statistics, 2018, 6(1): 1–12. DOI: 10.1007/s40304-018-0127-z |
| [30] | BHATTACHARYA K, HOSSEINI B, KOVACHKI N B, et al. Model reduction and neural networks for parametric PDEs[J]. Journal of Computational Mathematics, 2021, 7: 121–157. |
| [31] | SMITH J D, AZIZZADENESHELI K, ROSS Z E. EikoNet: solving the Eikonal equation with deep neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(12): 10685–10696. DOI: 10.1109/TGRS.2020.3039165 |
| [32] | TRENTI M, HUT P. N-body simulations (gravitational)[J]. Scholarpedia, 2008, 3(5): 3930. DOI: 10.4249/scholarpedia.3930 |
| [33] | BAGLA J S. TreePM: a code for cosmological N-body simulations[J]. Journal of Astrophysics and Astronomy, 2002, 23(3): 185–196. |
| [34] |
张文生. 科学计算中的偏微分方程有限差分法[M]. 北京: 高等教育出版社, 2006: 115-185. ZHANG W S. Finite difference methods for partial differential equations in science computation[M]. Beijing: Higher Education Press, 2006: 115-185. |
| [35] | LE BAIL R C. Use of fast Fourier transforms for solving partial differential equations in physics[J]. Journal of Computational Physics, 1972, 9(3): 440–465. DOI: 10.1016/0021-9991(72)90005-8 |
| [36] | CHOLLAMPATT S, NG H T. A multilayer convolutional encoder-decoder neural network for grammatical error correction[C]//Proceedings of the Thirty-Second Conference on Artificial Intelligence. 2018. |
| [37] | HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 770-778. |
| [38] | HE K M, SUN J. Convolutional neural networks at constrained time cost[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015: 5353-5360. |
| [39] | KINGMA D P, BA J. Adam: a method for stochastic optimization[C]//Proceedings of the International Conference on Learning Representations. 2015. |