2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
偏振测量是天体物理和太阳物理研究的强大观测手段,我们可以利用它直接获得天文目标的重要物理和几何信息,而这些信息是其他观测手段无法获得的。例如,太阳望远镜利用偏振光谱观测诊断太阳大气中的磁场结构[1];恒星发出的偏振辐射拥有更为丰富的物理内涵[2]。由于目标的低偏振特性,天文偏振测量始终处于一种光子饥饿的观测状态。因此,利用大口径望远镜收集更多的光子,以提高目标偏振信号的信噪比成为天文偏振测量的重要发展方向。望远镜的仪器偏振效应,即望远镜光学系统对入射偏振信号的改变,是当前高精度天文偏振测量面临的主要技术问题。对于大口径反射望远镜,仪器偏振主要由金属镜面的反射偏振效应引起。根据菲涅尔公式,金属镜面的损耗和延迟是入射角与镀膜材料折射率的函数。微观上,金属膜由大量线尺度在几十纳米的金属晶粒随机堆叠而成,其光学特性是镀膜材料、镀膜工艺、使用环境和时间的函数[3]。因此,为了能够准确把握金属薄膜的偏振特性,对望远镜进行准确的偏振光学设计或建模,并最终消除仪器偏振对偏振测量精度的影响,我们需要在实验室对金属镀膜材料的偏振特性进行精确全面的测量研究。
大口径望远镜常用铝膜反射镜,其偏振特性已广泛研究。纯铝膜镀制完成之后不久,在表面生成天然的氧化铝薄膜[4-5]。氧化铝薄膜在保护铝膜的同时也改变了铝镜的偏振特性,因此,在表征铝镜的偏振特性时,必须考虑氧化膜的影响[6]。然而氧化铝薄膜仍然不能阻止水分等污染,因此在镀完铝膜后继续在表面镀一层氧化硅保护膜[3, 7],偏振特性也会有很大的变化。
传统的椭偏测量法是对固定入射角度的椭偏光谱数据(ψ, Δ)进行拟合,在拟合过程中使用色散模型约束各个波长的折射率[8-10],有时还需要使用已知的文献值约束参数变化。因此,传统方法反演的参数准确度很大程度上依赖于色散模型的选取,而且由于自由度减少与参数假设等限制,对于复杂的样品需要建立十分复杂的结构模型才能进行较好的表征。
本文提出一种铝膜偏振特性测量方法,该方法首先对铝膜的缪勒矩阵关键元素进行直接测量,然后基于双层膜的结构模型,使用测得的缪勒矩阵数据在不依赖色散模型以及参数假设的情况下反演光学参数。
1 测量原理与方法天文目标发出的偏振辐射的偏振状态可以用斯托克斯(Stokes)向量表示,即Sin=(I Q U V)T,其中,I为入射光总强度;Q为垂直于水平偏振方向的强度参数;U为±45°偏振方向的强度参数;V为圆偏振的强度参数;上角标T表示矩阵转置。经过镜面反射后的斯托克斯向量表示为Sout=MSin,其中,M为镜面反射的缪勒矩阵,它的展开式为
| $ \boldsymbol{M}=\left[\begin{array}{cccc} m_{I \rightarrow I} & m_{Q \rightarrow I} & m_{U \rightarrow I} & m_{V \rightarrow I} \\ m_{I \rightarrow Q} & m_{Q \rightarrow Q} & m_{U \rightarrow Q} & m_{V \rightarrow Q} \\ m_{I \rightarrow U} & m_{Q \rightarrow U} & m_{U \rightarrow U} & m_{V \rightarrow U} \\ m_{I \rightarrow V} & m_{Q \rightarrow V} & m_{U \rightarrow V} & m_{V \rightarrow V} \end{array}\right], $ | (1) |
其中,矩阵各元素可以分为3类[11],按照下标描述为I→X(X=Q, U, V)表示仪器起偏;X1→X2≠1(X1, 2=Q, U, V)表示仪器串扰;X→X(X=Q, U, V)表示仪器退偏。
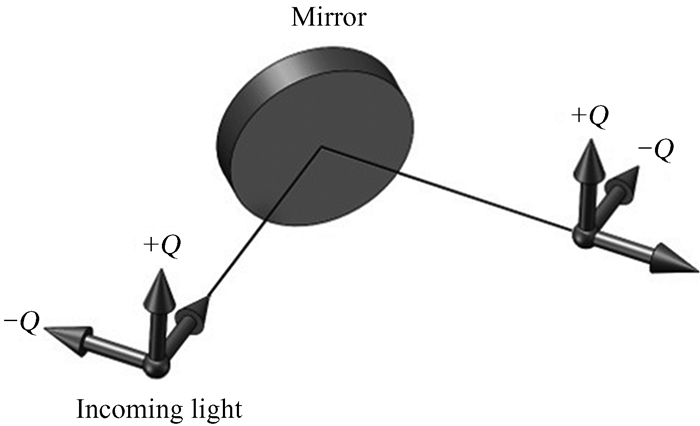
当入射与出射的斯托克斯向量按如图 1的偏振坐标系,即镜面反射变换的本征坐标系定义时,其中+Q对应光的s分量,金属镜面反射的缪勒矩阵可以简化为[12]
| $ \boldsymbol{M}=\left[\begin{array}{cccc} 1 & \cos 2 \psi & 0 & 0 \\ \cos 2 \psi & 1 & 0 & 0 \\ 0 & 0 & \sin 2 \psi \cos \Delta & \sin 2 \psi \sin \Delta \\ 0 & 0 & -\sin 2 \psi \sin \Delta & \sin 2 \psi \cos \Delta \end{array}\right], $ | (2) |
|
| 图 1 入射光与出射光的偏振坐标系 Fig. 1 The polarization coordinate frames of incoming and outgoing light |
其中,ψ和Δ为椭偏参数。考虑到金属反射缪勒矩阵的对称性, 偏振特性主要由mI→Q, mU→U和mV→U表征。因此,在随后的讨论中,缪勒矩阵仅指以上3个非0阵元。
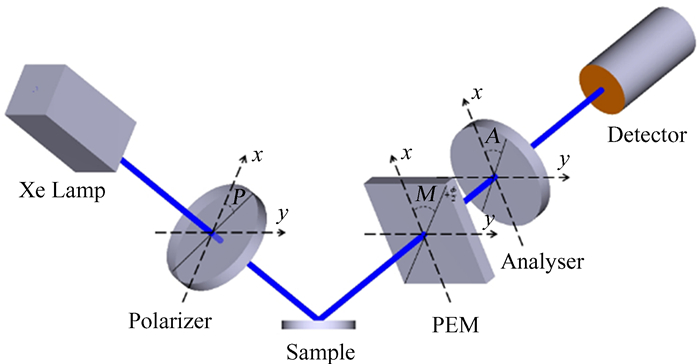
我们使用商业相位调制椭偏仪(UVISEL-Plus, Horiba)采集实验数据,系统光学结构如图 2。从光源(氙灯)发出的光经过一个起偏器(洛匈棱镜)后斜入射样品表面, 由于样品的偏振特性, 反射光的偏振发生改变, 经过光弹调制器(Photoelastic Modulator, PEM)和分析器(洛匈棱镜)的调制后由光谱仪探测,最后得到3个测量量(I0, Is, Ic)。这些量的大小取决于基于反射面的起偏器的方位角P、调制器的方位角M、分析器的方位角A和椭偏参数(ψ, Δ),表示为[13]
| $ \begin{aligned} &I_{0}=1+\cos 2 P \cos 2 M \cos 2(A-M)-[\cos 2 P+\cos 2 M \cos 2(A-M)] \cos 2 \psi , \\ &I_{\mathrm{s}}=\sin 2(A-M) \sin 2 P \sin 2 \psi \sin \Delta , \\ &I_{\mathrm{c}}=\sin 2(A-M)[\sin 2 M(\cos 2 \psi-\cos 2 P)+\sin 2 P \cos 2 M \sin 2 \psi \cos \Delta]. \end{aligned} $ | (3) |
|
| 图 2 相位调制椭偏仪的光学结构示意图 Fig. 2 Optical configuration of the phase modulation ellipsometer |
数据采集单元采集Is和Ic的数据。传统方法需要通过Is和Ic求得椭偏参数,然后把椭偏参数转化为样品的特性。此时求解椭偏参数需要进行反余弦或反正弦函数操作,其定义域限制在[-1, 1],由于Is和Ic微小的误差,计算过程中会超过定义域,导致计算错误。为了计算的准确性,我们可以直接通过对Is和Ic进行拟合研究铝镜的偏振特性。由(3)式可知,通过调整偏振器、调制器和分析器的方位角,我们可以得到不同的测量数据。对比(2)式可知,铝镜缪勒矩阵的几个非实数元素可以由两种调制下的Is和Ic表示,当P=45°,M=0°,A=45°时,
| $ \begin{aligned} &I_{\mathrm{s} 1}=\sin 2 \psi \sin \Delta ,\\ &I_{\mathrm{c} 1}=\sin 2 \psi \cos \Delta ;\\ \end{aligned} $ | (4a) |
当P=45°,M=45°,A=90°时,
| $ I_{\mathrm{s} 2}=\sin 2 \psi \sin \Delta ,\\ I_{\mathrm{c} 2}=\cos 2 \psi . $ | (4b) |
此时,我们可以直接测量缪勒矩阵的元素,相比于传统椭偏仪对椭偏参数的测量,可以得到反射镜更多的信息。铝镜测量数据用缪勒矩阵表示为
| $ \boldsymbol{M}_{\text {meas }}=\left[\begin{array}{cccc} 1 & I_{\mathrm{c} 2} & 0 & 0 \\ I_{\mathrm{c} 2} & 1 & 0 & 0 \\ 0 & 0 & I_{\mathrm{c} 1} & I_{\mathrm{s} 1} \\ 0 & 0 & -I_{\mathrm{s} 1} & I_{\mathrm{c} 1} \end{array}\right]. $ | (5) |
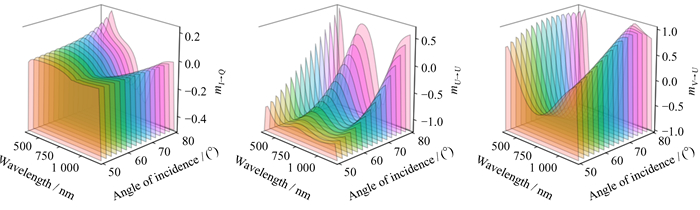
为了研究铝镜的偏振特性,我们需要获得足够多的信息,针对仪器的测量能力,我们采集铝反射镜样品(PF05-03-G01, THORLABS)在多入射角度(角度范围50~80°,间隔2°)下的光谱数据(波长范围400~1 200 nm,间隔25 nm)。图 3显示了测量得到的缪勒矩阵关键项(mI→Q,mU→U,mV→U),高度轴代表元素的大小。由图 3可以看出,这3个缪勒矩阵元素的光谱随着入射角的变化有明显变化。
|
| 图 3 测量得到的缪勒矩阵关键元素 Fig. 3 The key elements of measured Mueller matrix |
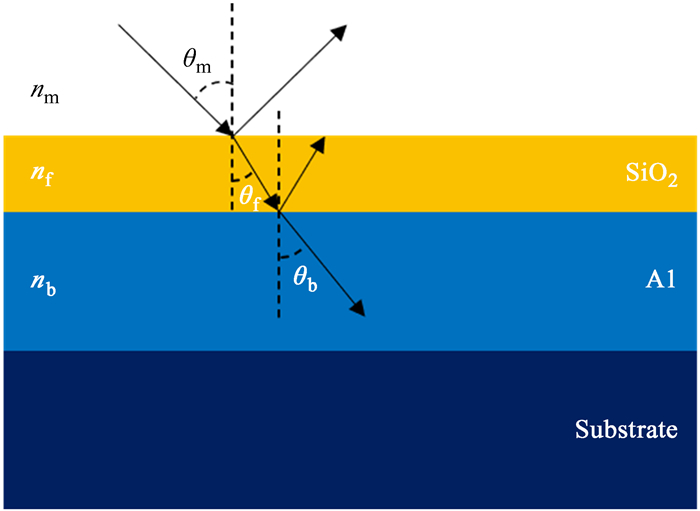
与纯铝膜相比,加了氧化硅保护层铝镜的偏振特性变得更加复杂。图 4给出了理想情况下带有保护层铝膜的分层结构, 其中,nm为空气的折射率;nf为氧化硅的折射率;nb为金属铝的复折射率(定义nb=nr-iκ);θm为光线在空气中的入射角;θf是氧化层内的折射角;θb为复数,不再有简单的折射角意义, 但仍然服从斯涅尔(Snell)定律。因此符合图 4的菲涅尔(Fresnel)反射系数为
| $ r=\frac{\left(\eta_{\mathrm{m}}-\eta_{\mathrm{b}}\right) \cos \delta_{\mathrm{f}}+\mathrm{i}\left(\frac{\eta_{\mathrm{b}}}{\eta_{\mathrm{f}}}-\eta_{\mathrm{f}}\right) \sin \delta_{\mathrm{f}}}{\left(\eta_{\mathrm{m}}+\eta_{\mathrm{b}}\right) \cos \delta_{\mathrm{f}}+\mathrm{i}\left(\frac{\eta_{\mathrm{b}}}{\eta_{\mathrm{f}}}+\eta_{\mathrm{f}}\right) \sin \delta_{\mathrm{f}}}, $ | (6) |
|
| 图 4 保护铝膜的理想结构模型示意图 Fig. 4 The ideal structural model of protected aluminum coating |
其中,δf为氧化膜的相位厚度,
| $ \begin{cases}s-\text { component: } & \eta_{j}=n_{j} \cos \theta_{j} \\ p-\text { component: } & \eta_{j}=n_{j} / \cos \theta_{j}\end{cases}. $ | (7) |
根据(2)式和(6)式,并结合椭偏参数的定义ψeiΔ=rp/rs,我们可以为图 4的结构建立偏振模型
| $ \boldsymbol{M}=\boldsymbol{f}\left[n_{\mathrm{r}}(\lambda), \kappa(\lambda), n_{\mathrm{f}}(\lambda), d_{\mathrm{f}}, n_{\mathrm{m}}, \lambda, \theta_{\mathrm{m}}\right], $ | (8) |
其中,nm,nr,κ和nf都是λ的函数。
由(8)式可以得出偏振特性与物理参数之间的关系,本文假设nm=1。特定入射角与特定波长下的缪勒矩阵关键项mI→Q,mU→U,mV→U与光学参数的关系为
| $ \left\{\begin{array}{llll} m_{I \rightarrow Q}=f_{1}\left(n_{\mathrm{r}}, \right. & \kappa, & n_{\mathrm{f}}, & \left.d_{\mathrm{f}}\right) \\ m_{U \rightarrow U}=f_{2}\left(n_{\mathrm{r}}, \right. & \kappa, & n_{\mathrm{f}}, & \left.d_{\mathrm{f}}\right) \\ m_{V \rightarrow U}=f_{3}\left(n_{\mathrm{r}}, \right. & \kappa, & n_{\mathrm{f}}, & \left.d_{\mathrm{f}}\right) \end{array} .\right. $ | (9) |
若使用测量的缪勒矩阵元素,并利用上述关系求解光学参数,此时只能建立3个方程。本文的方法不使用任何文献值,需要求解4个参数,方程个数小于未知数的个数,无法求解。多个入射角数据在单层铝膜时不能得到更多的信息,而对于带氧化层的结构,光在氧化层间多次反射后,不同入射角可以提供额外的信息[14]。因此,我们可以加入更多入射角度的测量数据以增加方程个数,每增加一个入射角度,可以增加3个方程,理论上只需要两个角度就可以实现对光学参数的超定, 一般使用尽可能多的方程反演光学参数。光学参数之间存在相关性,例如df和κ是正相关[15],为了限制相关性的影响,我们同时拟合多个波长的数据,每个波长的κ值不同,而df是统一的。在拟合光谱数据时,传统方法习惯使用色散模型对各个波长的折射率进行约束且只使用单个入射角的数据,拟合效果与反演参数准确度高度依赖模型的选取,而且由于自由度的减少与参数假设等限制,复杂的样品需要建立十分复杂的结构模型才能进行完整的表征。本文基于图 4的双层膜结构模型,使用多个入射角的光谱数据,同时拟合多个波长点的nr,κ,nf与共同的df,且不使用色散模型,此反演方法自由度更高,能够对多个入射角的光谱数据进行表征。我们使用Levenberg-Marquardt算法[16]解决这个非线性最小二乘优化的问题:
| $ \min \sum\limits_{i=1}^{n}\left[\left(I_{\mathrm{c} 2}-m_{I \rightarrow Q}\right)^{2}+\left(I_{\mathrm{c} 1}-m_{U \rightarrow U}\right)^{2}+\left(I_{\mathrm{s} 2}-m_{V \rightarrow U}\right)^{2}\right]_{i}, $ | (10) |
其中,n为铝镜缪勒矩阵的个数;mI→Q,mU→U和mV→U分别为计算得到的关键项。
入射角的数据越多提供的信息越多, 反演未知参数的精度也越高,因此,我们用上文描述的方法同时拟合50~80°入射角的光谱数据,并使用传统方法反演结果作为对比。在传统方法中,铝膜复折射率使用Drude-Lorentz色散模型,氧化硅使用Lorentz色散模型,然后分别对入射角60°和70°(入射角选在样品的赝布儒斯特角附近,测量数据灵敏度高)的ψ与Δ数据进行拟合。
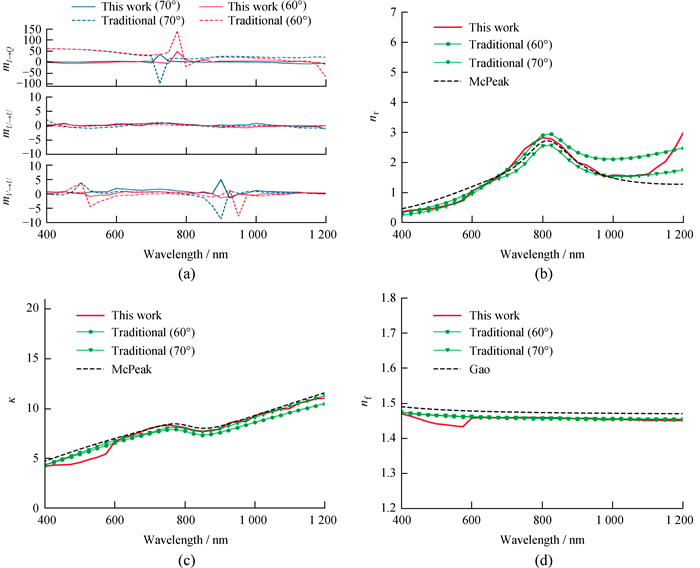
拟合效果由计算值和原始数据残差与原始数据的比值决定,记为相对残差,单位为百分比。图 5(a)是两种方法在60°和70°入射角的相对残差,其中实线代表本文方法的相对残差,虚线代表传统方法的相对残差。对于mI→Q,mU→U和mV→U,本文提出的方法比传统方法的拟合效果好,尤其是mI→Q元素,传统方法的相对残差在50%左右,而本文方法的相对残差几乎为0。本文方法是对多个入射角的数据进行拟合,得到的拟合结果符合多入射角的偏振特性,对于其他角度的相对残差也能达到相同的水平。此外,两种方法的残差曲线中同时出现相对残差突然变大的波长点,这是因为样品在这个波长点的偏振特性特别弱,几乎为0(例如在入射角70°时,其中一个突变点725 nm处的仪器起偏特性只有7×10-4),作为分母求得的相对误差会变得特别大。若不考虑个别突变点,两条曲线相比,可以看出本文方法的拟合效果更好。表 1显示了两种方法反演的氧化层厚度,它们之间只相差0.5 nm左右,两种方法测得的厚度基本一致。
|
| 图 5 (a) 两种方法在60°和70°入射角时测量数据的相对残差;(b),(c)和(d)分别为两种方法反演的nr,κ和nf随波长变化的对比图 Fig. 5 (a) The relative residuals for measured data by this work and traditional method at 60°and 70°; (b) (c) (d) is the comparison of results for the dependence of wavelength of nr, κ, nf, respectively |
| This work | Traditional(60°) | Traditional(70°) | |
| df/nm | 190.587 5 | 190.258 9 | 190.033 7 |
两种方法拟合的光学参数与文献参考值对比如图 5(b),(c)和(d),其中,实线是由多个波长点的结果平滑连接而成,虚线是铝膜复折射率(来自文[9])与氧化硅的折射率(来自文[17])的文献参考曲线。对于nr,κ与nf,图中3条曲线的变化趋势基本保持一致,只是本文方法与传统方法在数值上略有差别,一是因为传统方法使用色散模型不能完全表征反射镜的偏振特性,忽略了很多影响偏振特性的因素,二是因为本文方法考虑了mI→Q的变化特性。尤其是图 5(b),本文方法与参考曲线在大于1 000 nm波段的差异明显增大,参考曲线是由传统方法求得,也是在70°入射角对铝膜样品进行的测量。因此,参考曲线与传统方法在70°测量本文的样品十分相近,但在大于1 000 nm的波段有所差异。对于传统方法在入射角60°的结果,同样在大于1 000 nm波段与参考曲线有所差异。因此,本文方法与参考曲线的差异可以认为是样品的差异导致。而本文方法与传统方法曲线之间的差异可以认为是不考虑样品各向异性的前提下,均衡多个入射角偏振特性的结果。本文方法的曲线不够平滑,是因为本文方法没有使用色散模型等对光学参数随波长的变化趋势进行约束,只使用共同的氧化膜厚度建立各个波长点之间的联系,得到的结果反而能够真实反映当前波长点的偏振特性。
3 结论本文首先介绍了对保护铝膜的缪勒矩阵关键元素进行直接测量的原理和方法,然后介绍了在不依赖色散模型以及参数假设的情况下反演光学参数的方法和结果。实验结果表明,该方法反演得到的光学参数与传统方法的结果一致。相比于传统方法,该方法获取了更多的偏振特性信息,且自由度更高,能够对偏振特性(尤其是仪器起偏特性mI→Q)进行更好的表征。本文方法的结果曲线不够平滑,因为本文方法没有使用色散模型等对光学参数随波长的变化趋势进行约束,得到的结果反而能够真实反应当前波长点的偏振特性。本文方法是对多个入射角的数据进行拟合,得到的反演结果符合多入射角的偏振特性,而且基于简单的双层膜结构,更有利于未来对未知入射角的偏振特性进行预测和验证。
| [1] |
彭建国, 袁沭, 金振宇. 弱偏振器件Mueller矩阵测量的校准及应用[J]. 天文研究与技术, 2018, 15(1): 95–103 PENG J G, YUAN S, JIN Z Y. Calibration of Mueller matrix measurement of weak polarization element and its application[J]. Astronomical Research&Technology, 2018, 15(1): 95–103. |
| [2] |
辛玉新, 屈中权, 范玉峰, 等. 丽江2.4米望远镜检偏器控制系统设计[J]. 天文研究与技术, 2012, 9(1): 1–2 XIN Y X, QU Z Q, FAN Y F, et al. Design of a polarization-analyzer control system for the Lijiang 2.4m telescop[J]. Astronomical Research&Technology, 2012, 9(1): 1–2. |
| [3] | FELLER A, KRISHNAPPA N, PLEIER O, et al. Reflectivity, polarization properties, and durability of metallic mirror coatings for the European Solar Telescope[C]//Proceedings of SPIE. 2012. |
| [4] | MOTT N F. A theory of the formation of protective oxide films on metals[J]. Transactions of the Faraday Society, 1939, 35: 1175. DOI: 10.1039/tf9393501175 |
| [5] | JEURGENS L P H, SLOOF W G, TICHELAAR F D, et al. Structure and morphology of aluminium-oxide films formed by thermal oxidation of aluminium[J]. Thin Solid Films, 2002, 418(2): 89–101. DOI: 10.1016/S0040-6090(02)00787-3 |
| [6] | BURGE D K, BENNETT H E. Effect of a thin surface film on the ellipsometric determination of optical constants[J]. Journal of the Optical Society of America, 1964, 54(12): 1428. DOI: 10.1364/JOSA.54.001428 |
| [7] | WILSON R N. Reflecting telescope optics Ⅱ: manufacture, testing, alignment modern techniques[M]. New York: Springer, 1999. |
| [8] | RAKIĆ A D, DJURIŠIĆ A B, ELAZAR J M, et al. Optical properties of metallic films for vertical-cavity optoelectronic devices[J]. Applied Optics, 1998, 37(22): 5271–5283. DOI: 10.1364/AO.37.005271 |
| [9] | MCPEAK K M, JAYANTI S V, KRESS S J P, et al. Plasmonic films can easily be better: rules and recipes[J]. ACS Photonics, 2015, 2(3): 326–333. DOI: 10.1021/ph5004237 |
| [10] | CHENG F, SU P H, CHOI J, et al. Epitaxial growth of atomically smooth aluminum on silicon and its intrinsic optical properties[J]. ACS Nano, 2016, 10(11): 9852–9860. DOI: 10.1021/acsnano.6b05556 |
| [11] | KELLER C U. Instrumentation for astrophysical spectropolarimetry[M]//TRUJILLO-BUENO J, MORENO-INSERTIS F, SANCHEZ F. Astrophysical Spectropolarimetry. Cambridge: Cambridge University Press, 2010: 303-354. |
| [12] | AZZAM R M A, BASHARA N M. Ellipsometry and polarized light[M]. Amsterdam: North Holland Publishing Company, 1977. |
| [13] | FUJIWARA H. Spectroscopic ellipsometry: principles and applications[M]. New Jersey: John Wiley&Sons Incorporation, 2007. |
| [14] | TOMPKINS H G, HILFIKER J N. Spectroscopic ellipsometry: practical application to thin film characterization[M]. New York: Momentum Press, 2016. |
| [15] | DE JUAN OVELAR M, SNIK F, KELLER C U, et al. Instrumental polarisation at the Nasmyth focus of the E-ELT[J]. Astronomy&Astrophysics, 2014, 562: 1–8. |
| [16] | MARQUARDT D W. An algorithm for least-squares estimation of nonliner paramenters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441. DOI: 10.1137/0111030 |
| [17] | GAO L, LEMARCHAND R, LEQUIME M. Refractive index determination of SiO2 layer in the UV/Vis/NIR range: spectrophotometric reverse engineering on single and bi-layer designs[J]. Journal of the European Optical Society, 2013, 8: 13010. DOI: 10.2971/jeos.2013.13010 |



