2. 中国科学院大学天文与空间科学学院, 北京 100049
2. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100049, China
卫星导航接收机通常使用载波辅助的载波跟踪环和码跟踪环实现载波跟踪和码跟踪[1-2]。码跟踪环通常使用非相干延迟锁定环(Delayed Lock Loop, DLL)实现,通过接收I和Q两路信号,分别产生超前、即时、滞后的6组信号,利用全球导航卫星系统伪随机码的自相关特性,用鉴相器计算本地产生的码与接收码的相位差;在获得相位差的同时,将鉴相结果输入数字控制振荡器(Numerically Controlled Oscillator, NCO),调节本地产生的伪码相位,使之与输入的码相位对齐,完成码跟踪,同时得到码相位测量值,用于计算伪距。以全球定位系统(Global Positioning System, GPS)为例,全球定位系统的码速率为1.023 MHz,一个码片的长度为293 m,码伪距测量误差约为一个码片长度的1%,大约为3 m。
为得到更高精度的码相位观测值,国内外许多学者尝试改善码环的结构或用其他方法提高码环的鉴相精度。文[3-4]在快速傅里叶变换的基础上提出内插思想,提取相关峰的最高点和最低点,进行插值处理提取相位,解决了傅里叶变换计算量大的问题,但是精度没有提高。文[5-6]在其基础上提出二次插值的方法获取更精准的码相位测量结果,在信号强的情况下表现良好。文[7]采用最小二乘法拟合提高码相位测量精度,该方法相较于插值法有实现简单、精度高的特点,但测量范围较小,仅适合码相位误差在一个采样点以内测量。文[8]提出基于整体最小二乘法的估计算法[8],虽然精度有所提高,但需要进行矩阵的奇异值分解等运算,运算量过大。深空探测中使用再生伪码提高码相位测量精度[9-11],再生伪码信号的码相位估计依赖码元中存在显著的时钟分量,利用这一特性,依次实现码片时钟和码相位同步,两者实质上分别对应小数位和整数位的码相位值,但目前没有应用于全球导航卫星系统接收机。全球导航卫星系统接收机中提高码跟踪环相位精度的方式主要在于环路的参数设置与选取[12-13],通过设置自适应变化环路带宽,实时调整环路参数,提高跟踪环路的精度。文[14-16]提出使用卡尔曼滤波跟踪环代替传统码相位跟踪环,提高了环路的跟踪性能与动态范围,降低了码相位误差与抖动,但是计算量过大不利于实际应用。文[17]提出使用相位条纹对码相位进行测量的方法,结果表明,相位条纹法比传统全球定位系统接收机中鉴相精度有所提高,但是由于使用仿真数据进行模拟,缺乏实测数据的验证。
针对以上问题,本文在文[17]的基础上引入实际全球定位系统信号,针对伪码信号的互相关功率谱,对传统的跟踪环进行改进,提出一种高精度的码相位测量方法。
1 相位条纹法测量码相位 1.1 相位条纹法基本原理相位条纹法通常用于测量两台接收机之间的距离。同一信号经不同路径到达两台接收机后,通过相关计算得到相位差,从而计算到达时间差τ,乘以光速得到两台接收机之间的距离。设两台接收机接收的信号分别为f1(t)和f2(t),其中f2(t)=f1(t-τ),τ为信号到达两台接收机的时延。对两路时域信号做傅里叶变换,并进行互相关,得到的互相关功率谱为
| $ {S_{12}}\left( \omega \right) = {F_1}\left( \omega \right){F_2}^*\left( \omega \right) = F_1^2\left( \omega \right){e^{j\omega \tau }}, $ | (1) |
互相关功率谱的相位为
| $ \phi = \omega \tau = 2{\rm{ \mathsf{ π} }}\tau f. $ | (2) |
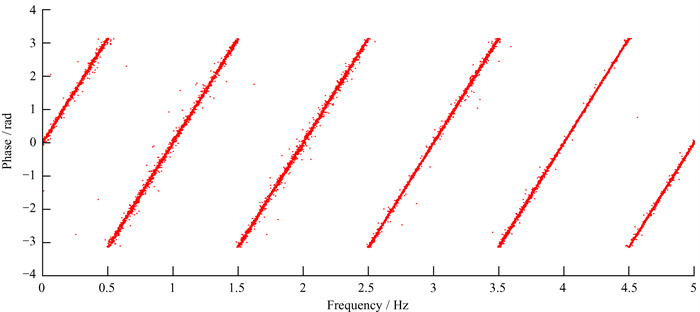
可以看出,在两台接收机时延τ一定的情况下,互相关功率谱相位ϕ与信号的频率f呈线性关系,斜率为2πτ。通常相位ϕ的取值范围为[-π, π],将ϕ~f斜线按照[-π, π]的范围切割成周期性条纹,条纹之间的间隔T0为
| $ {T_0} = \frac{{2{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }}\tau }} = \frac{1}{\tau }, $ | (3) |
而条纹出现的频率f0为
| $ {f_0} = \frac{1}{{{T_0}}}, $ | (4) |
即通过统计条纹出现的频率,可以得到信号的时延,如图 1。
|
| 图 1 相位条纹示例 Fig. 1 Phase strip example |
在全球导航卫星系统接收机中,接收的信号经过下变频剥离载波后得到基带信号,基带信号与本地数字控制振荡器产生的伪码信号可以视作两路相关的具有时延的信号。通过计算其中的待测时延可以得到本地信号与接收信号的码相位差,从而得到更高精度的码相位测量值。接收机在下变频后通常得到I和Q两个正交的支路,选取I支路的即时信号剥离载波并与本地数字控制振荡器产生的码信号做相关运算,得到互相关功率谱,通过统计出现的相位条纹频率,测得接收信号的时延。
但由于接收的导航信号信噪比较低,直线拟合的效果较差,故首先对接收信号与本地信号进行时域上的分段叠加,提高信号的信噪比。对相位条纹曲线ϕ(f)再做一次傅里叶变换,当条纹频率为f0,条纹间隔T0=1/f0时,单个条纹ϕ1(f)可以表示为
| $ \phi_{1}(f)=f\left[u\left(f+\frac{1}{2 f_{0}}\right)-u\left(f-\frac{1}{2 f_{0}}\right)\right], $ | (5) |
对ϕ1(f)做傅里叶变换,频谱的幅度为
| $ \left| {{\mathit{\Phi }_1}(\psi )} \right| = 2\left( {\frac{{\sin \frac{\psi }{{2\pi }}}}{{{\psi ^2}}} - \frac{{\cos \frac{\psi }{{2\pi }}}}{\psi }} \right). $ | (6) |
因为条纹以T0为周期出现,周期性条纹的相位傅里叶变化为
| $ |\mathit{\Phi }(\psi )| = 2\sum\limits_{n = 1}^{ + \infty } {\frac{{\delta \left( {\psi - 2\pi n{f_0}} \right)}}{n}} . $ | (7) |
由(7)式可知,相关条纹ϕ(f)在进行傅里叶变化后得到的幅度谱∣Φ(ψ)∣,当n=1时,∣Φ(ψ)∣最大,此时ψ=2πf0。
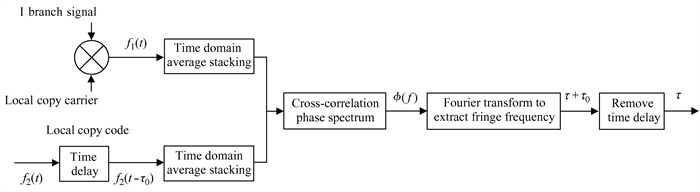
另外,由于接收机在跟踪信号时,本地数字控制振荡器产生的伪码与接收的伪码信号小于1个码片,时延τ较小,相位条纹出现的频率较低。为了更加明显地获得相位条纹,可以在本地接收信号时预先补偿一个时延τ0,令τ0>>τ,在整体时延变大以后可以获得频率条纹数量,有利于得出更精确的时延。在通过条纹频率计算出τ0+τ以后,减去补偿时延τ0,最后得到待测时延τ,即可得到码相位测量值。相位条纹法测量码相位流程如图 2。
|
| 图 2 相位条纹法测量码相位流程图 Fig. 2 Flow chart of phase fringe method to measure code phase |
克拉美罗下界(Cramer-Rao Lower Bound, CRLB)用于计算无偏估计能够获得最佳估计精度,因此经常用于计算理论能达到的最佳估计精度,评估参数估计方法的性能。
信号经过下变频后的中频信号为
| $ x(n)=A D(t) \cos \left(2 \pi f_{\mathrm{IF}} n+\tau\right)+n_{1}, $ | (8) |
其中,A为信号的幅值;τ为待测码相位;nI为方差为σ的高斯白噪声,其余量均为常量。
似然函数为
| $ p(x;\tau ) = \frac{1}{{2\pi {\sigma ^2}}}\exp \left\{ {\frac{{ - \sum\limits_{n = 0}^{N - 1} {{{\left[ {x(n) - A\cos \left( {2\pi {f_{{\rm{IF}}}}n + \tau } \right)} \right]}^2}} }}{{2{\sigma ^2}}}} \right\}. $ | (9) |
其对数一阶偏导为
| $ \frac{\partial \ln p(x ; \tau)}{\partial \phi}=\frac{-A}{\sigma^{2}} \sum\limits_{n=0}^{N-1}\left\{x(n) \sin \left(2 \pi f_{\mathrm{IF}} n+\tau\right)-A \sin \left(4 \pi f_{0} n+2 \tau\right)\right\}^{2} . $ | (10) |
二阶偏导为
| $ \frac{\partial^{2} \ln p(x ; \tau)}{\partial \phi^{2}}=\frac{-A}{\sigma^{2}} \sum\limits_{n=0}^{N-1}\left\{x(n) \cos \left(2 \pi f_{\mathrm{IF}} n+\tau\right)-A \cos \left(4 \pi f_{0} n+2 \tau\right)\right\} . $ | (11) |
二阶偏导的期望为
| $ -E\left[\frac{\partial^{2} \ln p(x ; \tau)}{\partial \phi^{2}}\right]=\frac{A}{\sigma^{2}} \sum\limits_{n=0}^{N-1}\left[E\{x(n)\} \cos \left(2 \pi f_{\mathrm{IF}} n+\tau\right)-A \cos \left(4 \pi f_{0} n+2 \tau\right)\right], $ | (12) |
其中,期望
| $ -E\left[\frac{\partial^{2} \ln p(x ; \tau)}{\partial \phi^{2}}\right]=\frac{A^{2}}{2 \sigma^{2}}\left[\sum\limits_{n=0}^{N-1} 1-\sum\limits_{n=0}^{N-1} \cos \left(4 \pi f_{0} n+2 \tau\right)\right] \approx \frac{N A^{2}}{2 \sigma^{2}}=N R_{\mathrm{SN}} $ | (13) |
其中,N为信号长度;RSN为信号的信噪比。所以,中频信号的克劳美罗下界为
| $ \operatorname{var}\{\tau\} \geqslant \frac{1}{N R_{\mathrm{SN}}} . $ | (14) |
相位条纹法在计算时通过时域叠加提高信号的信噪比,因此可以使克拉美罗下界更低,提高估计精度。
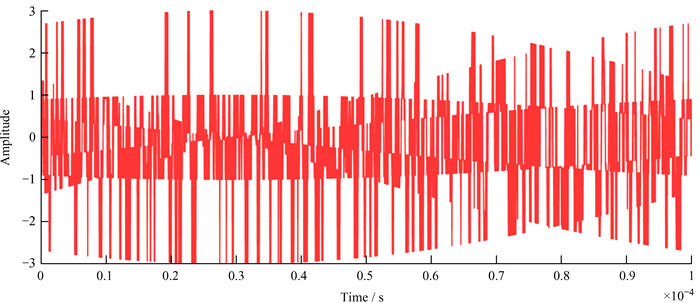
2 实际全球导航卫星系统信号实验本次实验使用数字采集卡采集的全球定位系统信号对上述方法进行验证。实验选用的采集卡为NSL Stereo,采样频率为26 MHz,中频载波频率为6.5 MHz。对全球定位系统的PRN32卫星数据进行采集,其中,信号长度为100 μs,码速率为1.023 MHz,设定的补偿时延τ0为600 ns。处理过程在MATLAB上完成,处理过程如图 3~图 5。
|
| 图 3 采集的中频信号 Fig. 3 IF signal collected |
|
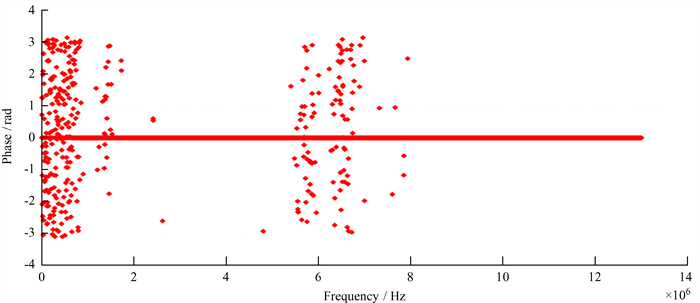
| 图 4 本地码与接收码互相关功率谱相位条纹ϕ(f) Fig. 4 Local code and received code cross-correlation power spectrum phase strip ϕ(f) |
|
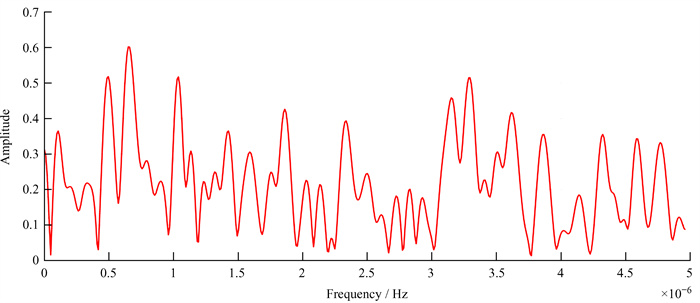
| 图 5 对相位条纹进行傅里叶变换提取条纹频率Φ(ψ) Fig. 5 Perform Fourier transformation on phase strip to extract strip frequency Φ(ψ) |
图 3为采集的数据中截取100 μs的长度部分,通过混频处理后剥离中频载波,留下伪码信号,与本地产生的PRN32卫星的码做相关运算,得到相关频率条纹ϕ(f),如图 4。对ϕ(f)进行傅里叶变换,得到功率谱∣Φ(ψ)∣的最大值对应的频率即为需要测得的时延τ+τ0,即图 5中∣Φ(ψ)∣最大值对应的频率为所测时延τ+τ0。经计算,τ+τ0 =607.6 ns,减去τ0=600 ns,最后得到τ=7.6 ns,乘以光速后得到鉴相误差为2.28 m。
接收机的跟踪环路在进行稳定的跟踪后,理论热噪声误差为
| $ \sigma_{\mathrm{n}}=\sqrt{\frac{B_{\mathrm{n}}}{C N_{0}}\left(1+\frac{1}{2 C N_{0} T}\right)} . $ | (15) |
将误差转化为距离,可得
| $ \sigma_{\mathrm{n}, \mathrm{M}}=\frac{\lambda}{2 \pi} \sqrt{\frac{B_{\mathrm{n}}}{C N_{0}}\left(1+\frac{1}{2 C N_{0} T}\right)} . $ | (16) |
其中,CN0为接收机的载噪比;Bn为噪声带宽;T为相关积分时间。在本次实际采样的数据中,载噪比通过采样数据计算,CN0=42.6 dB·Hz。传统的接收机积分时间为T=1 ms,Bn=2 Hz,在载噪比为42.6 dB·Hz时,理论热噪声误差上限为σn, M=36.059 m,实际使用传统延时锁定环测量结果为5.39 m。通过相位条纹法计算的误差为2.28 m,优于传统锁相环中非相干点积功率法鉴相的理论误差。
3 结论传统全球导航卫星系统接收机在实际跟踪中的鉴相误差在0.1个码片左右,即2.93 m,通过本文方法得到的误差为2.28 m,性能提高了23%。在实际的接收机中,本文为提供高精度的码相位计算给出了一种方法,得到更高精度的伪距测量值。在后续的工作中,需要对相位条纹法中的参数选取进行进一步的研究。
| [1] |
鲁郁. 北斗/GPS双模软件接收机原理与实现技术[M]. 北京: 电子工业出版社, 2016. LU Y. Principle and implementation technology of Beidou/GPS dual-mode software receiver[M]. Beijing: Publishing House of Electronics Industry, 2016. |
| [2] |
谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2017. XIE G. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2017. |
| [3] | KRASNER N. GPS receiver and method for processing GPS signals: US20030139879A1[P/OL]. 2003-07-24[2021-04-06]. https://patents.google.com/patent/US20030139879A1/en?oq=US20030139879A1. |
| [4] | KAPLAN E D, HEGARTY C. Understanding GPS/GNSS: principles and applications[M]. Norwood: Artech House Publishers, 2017. |
| [5] |
张波, 郭英, 齐子森, 等. PN码相位精确测量的累加最小二乘法[J]. 北京航空航天大学学报, 2016, 42(10): 2265–2270 ZHANG B, GUO Y, QI Z S, et al. Precise measurement of PN code phase by accumulative least square method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2265–2270. |
| [6] |
龚国辉, 李思昆. 提高DSSS信号PN码相位测量精度的三点二次插值法[J]. 通信学报, 2007(2): 130–133 GONG G H, LI S K. Improving DSSS signal PN code phase measurement precision by 3-points quadratic interpolation[J]. Journal on Communications, 2007(2): 130–133. |
| [7] |
胡修林, 张俊, 杨灵. 直接序列扩频通信系统中PN码相位的精确测量方法[J]. 电讯技术, 2005(4): 128–131 HU X L, ZHANG J, YANG L. A method for accurately measuring the phase of PN code in DSSS systems[J]. Journal Electronic, 2005(4): 128–131. |
| [8] |
罗海军, 彭卫东. 整体最小二乘法在精同步中的应用[J]. 计算机测量与控制, 2014, 22(7): 2291–2294 LUO H J, PENG W D. Application of total least squares in precise synchronization[J]. Computer Measrewment&Control, 2014, 22(7): 2291–2294. DOI: 10.3969/j.issn.1671-4598.2014.07.088 |
| [9] | BOSCAGLI G, HOLSTERS P, VASSALLO E, et al. PN regenerative ranging and its compatibility with telecommand and telemetry signals[J]. Proceedings of the IEEE, 2007, 95(11): 2224–2234. DOI: 10.1109/JPROC.2007.905186 |
| [10] |
彭保童, 马宏, 毛鑫峰. 基于再生伪码测距的复合码分析[J]. 电子测量技术, 2017, 40(10): 171–175 PENG B T, MA H, MAO X F. Analysis of complex code based on regenerated pseudo-code ranging[J]. Electronic Measurement Technology, 2017, 40(10): 171–175. |
| [11] |
侯彦兵, 焦义文, 杨文革. 基于遥测信号的测距技术及其发展趋势[J]. 电讯技术, 2019, 59(7): 863–868 HOU Y B, JIAO Y W, YANG W G. Telemetry-based ranging technology and its development trend[J]. Telecommunication Engineering, 2019, 59(7): 863–868. DOI: 10.3969/j.issn.1001-893x.2019.07.020 |
| [12] |
孙慧萍, 张丽, 王利红, 等. GPS软件接收机码跟踪环的参数设计[J]. 山西大同大学学报(自然科学版), 2018, 34(2): 10–12 SUN H P, ZHANG L, WANG L H, et al. Parameter design of code tracking loop for GPS software receiver[J]. Journal of Shanxi Datong University (Natural Science), 2018, 34(2): 10–12. |
| [13] |
刘盟超, 赵丙风. GNSS接收机自适应带宽伪码跟踪环路设计[J]. 无线电通信技术, 2017, 43(4): 64–66, 79 LIU M C, ZHAO B F. Design of adaptive bandwidth DLL for GNSS receivers[J]. Radio Communications Technology, 2017, 43(4): 64–66, 79. |
| [14] | LASHELY M. Kalman filter based tracking algorithms for software GPS receivers[D]. Auburn: Auburn University, 2006. |
| [15] |
王丽华, 李博扬, 寇建辉. GPS接收机PLL与卡尔曼跟踪环路性能分析[J]. 现代导航, 2016(1): 28–33 WANG L H, LI B Y, KOU J H. Performance analysis on PLL and Kalman tracking loop of GPS receiver[J]. Modern Navigation, 2016(1): 28–33. |
| [16] | MIAO J F, CHEN W, SUN Y R, et al. Low C/N0 carrier tracking loop based on optimal estimation algorithm in GPS software receivers[J]. Chinese Journal of Aeronautics, 2010, 23(1): 109–116. |
| [17] |
傅圣友, 王兆瑞, 金声震, 等. 基于相位条纹的高精度GPS码相位测量方法[J]. 北京航空航天大学学报, 2019, 45(9): 1824–1830 FU S Y, WANG Z R, JIN S Z, et al. High-precision GPS code phase measurement method based on phase stripe[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(9): 1824–1830. |


