2. 暨南大学中法天体测量、动力学与空间科学联合实验室, 广东 广州 510632
2. Sino-French Joint Laboratory for Astrometry, Dynamics and Space Science, Jinan University, Guangzhou 510632, China
天体的光度测量主要研究天体的光度随时间的变化情况,光度变化能够反映天体的物理性质,对探究天体的演化规律有重要意义。文[1]从小行星的光变周期中分析自转周期和形状。文[2]研究了柯伊伯带(Kuiper belt)天体的光变周期,分析了其反照率等物理属性。文[3]利用中长周期光变研究类星体的物理属性。然而,天体高精度光度测量面临许多挑战。例如,由于地球大气的存在,天体的光度经过地球大气后产生一定的消光和折射效应,对天体的测量精度有较大的影响。由于相近(天空平面内角距离较小)的恒星之间相对位置变化较小且通过的大气相似,我们通常使用相对测光方法进行测量。而太阳系天体相对于恒星位置变化较快且经过的大气不同,绝对测光是一种更好的选择。在地面望远镜观测中,人们可以通过该方法准确地求出大气消光、夜间零点等系数。文[4]提供了标准星的详细参数和信息,为绝对测光研究奠定了良好的基础。尽管如此,绝对测光的精度不如相对测光。为了消除地球大气对光度测量的影响,随着科技的发展和进步,人们把探测器发射到太空,测光精度有了显著提高。
本文主要研究基于地面观测的光度测量技术和精度回报现象。在地面观测中,为了提高位置和光度的测量精度,我们通常选择在子午线附近的目标进行观测,以减小大气的影响。在天体测量中,文[5]发现两颗伽利略卫星相互靠近时有较高的位置测量精度,文[6]在此基础上开发了相互逼近天体测量技术,文[7]基于M35星团对该现象进行统计分析,把位置测量的精度回报现象进行特征化。在相对测光中,人们主要关注参考星光度的稳定性,而较少关注目标星与参考星在天空平面内的角距离。若相对测光也存在精度回报现象,即假设目标星存在许多不同相对距离的候选参考星,且这些参考星的光度相近、稳定,采用相对距离较小的参考星有较高的测量精度。基于中国科学院云南天文台1 m光学望远镜观测的M35星团资料,本文探究相对测光的精度回报现象。
1 光度测量工具与关键技术 1.1 光度测量工具目前有许多开放的光度测量工具和软件,例如IRAF (Image Reduction and Analysis Facility)能够较好地处理图像并进行测光,但需要在Linux环境下进行配置和操作。APT(Aperture Photometry Tool)是一款孔径测光的教学软件,能够方便地进行孔径测光、求取生长曲线等[8]。SExtractor广泛应用于深度巡天的目标源提取和测量。MaxIm DL除了可以批量平场处理、图像质量评估、图像堆叠外,还能孔径测光[9]。后来,随着计算机技术的发展和Python编程语言的兴起,PyRAF(https://pypi.org/project/pyraf/)和photutils(https://photutils.readthedocs.io/en/stable/index.html)成为测光的Python库。
1.2 MaxIm DL与photutils结合的测光技术Photutils是基于Python语言的测光库,也是Astropy的附属软件包,用户可以通过编程调用目标检测、光度测量等函数。DaoStarFinder和IRAFStarFinder是该库中用于目标检测的两个函数,分别调用DAOPHOT和IRAF的搜星程序。Photutils库提供了孔径测光和点扩散函数测光两种方法。本文主要使用和探究孔径测光方法,即photutils.aperture库。在该库中,孔径半径设置为浮点型数值可以为孔径测光提供更高的精度,而MaxIm DL和APT等测光软件的孔径半径数值只能设置为整数。此外,aperture_photometry函数中的exact方法能够精确处理孔径测光中包含像素的分数部分,相比划分子像素方法有更高的测量精度。
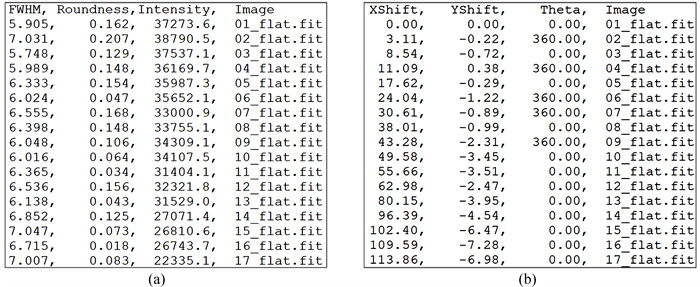
然而,使用photutils对地面的观测资料进行光度测量时存在一些问题。在目标检测(搜星)函数中,无论我们使用DaoStarFinder还是IRAFStarFinder方法,像素阈值和星像的半高全宽(Full Width at Half Maximum, FWHM)是必选的输入参数。通常,我们选择几倍背景像素的标准差作为输入像素阈值,而做巡天研究工作时需要把该参数设置得更小。要准确地搜索观测资料中的大部分星像,输入的半高全宽参数需要与每幅图像相近。当然,我们希望每个晚上观测资料的半高全宽是稳定的,这也需要天气与设备的配合。但实际上,在地面观测中,即使用同一台望远镜连续观测的图像,星像的半高全宽也有一定的波动。因此,在测光程序批量处理时,若使用一个大致的半高全宽作为目标检测函数的输入参数,则一些图像中大部分的星像不能检出。对于此类情况,我们可以把半高全宽与设定值相差较大的图像进行单独处理或编写自适应调整半高全宽参数的相关算法。由于上述方法操作或实现过程较复杂,本文提出了与MaxIm DL相结合的方法。MaxIm DL(本文使用5.24版本)在图像堆叠过程中提供了批量图像质量评估的功能,可以方便地导出每幅图像的半高全宽、圆度等信息(如图 1(a))。我们使用MaxIm DL输出每幅图像的半高全宽数据作为目标检测函数的输入参数,可以较好地解决图像之间星像半高全宽波动较大的问题。在实践中发现,目标检测函数中输入的半高全宽参数取MaxIm DL导出的数值再加上0.5有更好的搜星效果。
|
| 图 1 (a) 使用MaxIm DL导出的图像质量评估文件;(b)图像对齐文件 Fig. 1 (a) The image quality evaluation file exported by MaxIm DL; (b) image alignment file |
在光度测量过程中,分析和统计视场中所有星像的光变情况对变星巡天、星像特征分析有重要意义。如何把各图像的星像进行匹配是统计视场中所有星像光变的关键问题。对于相同恒星在各帧图像的像素坐标基本不变的观测资料来说,获取主帧所有星像的位置和光度信息能较好地与其他图像匹配,从而绘制目标的光变曲线。然而,观测时望远镜指向或跟踪不稳定,统计视场中所有星像的光度变化是不容易的。本文结合MaxIm DL对该问题提出了一种快速的解决方案。首先,使用MaxIm DL的对齐功能可以导出每幅图相对于第1幅图在像素坐标的偏移量(如图 1(b))。然后,在每幅图探测的星像坐标中减去相应的偏移量,此时,我们可以消除由于望远镜指向不稳定带来的视场偏移,进行各图像中星像的匹配和统计工作。但如果需要对各星像中更多信息进行分析和统计研究,我们需要采用基于星表匹配的方法,但该方法需要花费更长的时间。
2 相对测光中的精度回报现象受大气湍流的影响,CCD芯片中星像的位置与实际位置存在不同程度的偏差。由于视场内相近的两颗星受大气湍流的影响相似,星像的位置测量中存在精度回报效应,即星像之间角距离较小时相对位置测量有更高的精度。在相对测光中,我们猜测在同一视场内受不同大气质量的影响,各星像存在不同程度的消光。若相近的两颗星受大气消光影响的程度相似,则它们也有较高的相对测光精度。在本节中,我们统计M35星团的相对测光精度与相对距离的关系,探讨测光中的精度回报现象。
2.1 观测资料选取两颗相互靠近且光度不变的天体有利于探究精度回报现象。然而,我们很难找到角距离变化较大且光度不变的天体。对于太阳系小行星来说,虽然它能够与恒星相互靠近,但小行星受自转、相位、卫星等因素的影响,光度发生变化,不适用于探究精度回报现象的存在问题。若以一般的恒星作为实验观测目标,由于恒星之间的相对角距离几乎不变,找到测光精度与距离的关系比较困难。此外,也有不少恒星的亮度是变化的。在实验中,我们采用星团作为观测目标。星团中有大量的恒星,我们可以方便地统计距离与测光精度的关系。此外,星团能够反映精度回报现象是普遍存在的,而不是只发生在某个天区或个别天体上。因此,使用星团能够较好地探究相对测光的精度回报现象。然而,星团中也有光度发生变化或受其他天体光度影响较大的恒星,我们在2.2节中详细讨论对于这些恒星的处理。
2.2 资料处理与数据分析本文使用中国科学院云南天文台1 m光学望远镜(详细参数如表 1)拍摄的M35星团图像探究测光精度回报现象。我们在不同高度角对M35星团进行观测,观测时望远镜的指向稳定,具体的观测资料情况如表 2。
| Item | Parameter |
| Focal length | 1 330 cm |
| Diameter of primary mirror | 101.6 cm |
| CCD field of view | 16′ × 16′ |
| Size of pixel | 15 μm × 15 μm |
| Size of CCD array | 4 096 × 4 112 |
| Scale | ~0.234″/pixel |
| Date (y-m-d) | Frames (Filter I) | Altitude /° | Exptime /s | FWHM /pixel |
| 2020-12-08 | 16 | 83-89 | 40 | 5.5-6.5 |
| 2021-01-15 | 21 | 78-83 | 40 | 4.1-5.3 |
| 2021-01-15 | 20 | 43-50 | 50 | 4.6-6.0 |
| 2021-01-15 | 17 | 31-36 | 50 | 5.7-7.0 |
对于观测资料的预处理,我们先使用MaxIm DL做平场校正,用图像的质量评估功能筛选半高全宽较小且圆度较好的图像。表 1列出的图像帧数是经过质量评估筛选后的数量。在实际测光中,我们要慎重使用该方法进行图像质量的筛选,因为该方法可能把关键的光变数据剔除。在本实验中,探究相对测光精度回报现象的存在需要假定每颗恒星的光度不变,也需要尽可能地把光度发生变化的星像剔除,有效减小由于大气不稳定、焦距等因素造成的影响。
我们使用孔径测光的方法进行实验探究。由于星团中恒星的星像比较密集,使用环形区域估计各星像的背景值常常受到附近星像的干扰。因此,本文在每幅图像的星像中采用一个固定的天空背景值。具体地,我们先对每幅图像背景像素剔除3σ,然后采用“3-2”公式(3倍中值-2倍均值)[10]进行天空背景值的估计。接着,我们使用photutils测光库提供的函数搜星,结合MaxIm DL进行各星像光度的匹配和统计。因为我们需要假设每颗恒星在每组图像中的光度不变,故以相对测光仪器星等对每组图像的标准差进行衡量。由于暗星测光精度较低,我们选择信噪比较高的亮星统计星像的相对测光精度与相对距离之间的关系。这些亮星分布在视场的不同位置,我们将这些亮星两两进行较差测光,统计每组图像中星像相对测光精度和参考星相对像素距离之间的关系。这时,若每组图像中选出n颗亮星,每颗亮星都作为其他n-1颗星的参考星,共有n(n-1)组测光精度与距离的关系。
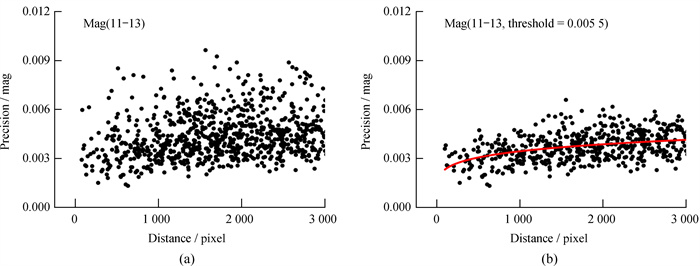
然而,以信噪比或星等为标准筛选的亮星光度也不一定是稳定的。若某一恒星是变星、双星系统或受附近亮星光度影响较大,该恒星的测光精度比较低,也不适用于统计和分析相对测光的精度回报现象。因此,我们需要尽可能找出这些测量精度较低的星并剔除。若一颗星的光度在一组图像中发生了较大的变化,不管与哪颗参考星进行相对测光,都有较低的精度。本文提出标准差均值的方法剔除测量精度较低的恒星:(1)先计算每颗恒星与视场中其他恒星的星等标准差,每颗星都能找到n-1组这样的标准差;(2)求出每颗星对于n-1组标准差的均值;(3)设定一个阈值(一般设置为星像精度集中的上方附近,如图 2(a)),剔除标准差的均值高于该阈值的星。使用该方法能够有效剔除精度不高的恒星,方便统计和探究测光精度回报现象是否存在。
|
|
图 2 (a) 2020年12月8日观测资料测光精度与相对距离之间的关系,统计了仪器星等为11~13 mag的数据。相对像素距离采用公式 |
图 2展示了2020年12月8日M35星团图像的测光精度与相对距离之间的关系,其中采用仪器星等为11~13 mag的恒星。图 2(a)是剔除之前的结果,图 2(b)采用标准差均值剔除的方法,设置阈值为0.005 5剔除后的结果。我们可以看到采用“标准差均值剔除”的方法能够有效剔除精度较差的星。
接着,我们使用同样的方法处理2021年1月15日共3组在不同高度角拍摄的M35星团资料,探究大气质量对测光精度回报现象的影响,结果如图 3~图 5。
|
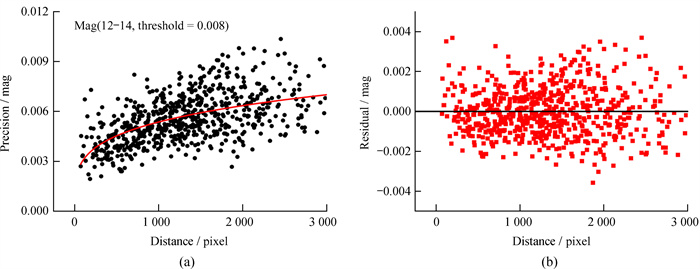
| 图 3 (a) 2021年1月15日观测资料(高度角为31°~36°,仪器星等为12~14 mag)测光精度与相对距离之间的关系,其中剔除阈值设置为0.008;(b)使用幂函数拟合后的残差随相对像素距离之间的分布情况 Fig. 3 (a) The relationship between the relative distance and photometric precision of the observations on Jan. 15, 2021 (the altitude is 31-36 deg and instrumental magnitude is 12-14 mag), in which the elimination threshold is set to 0.008; (b) the distribution of the residual fitted by power function |
|
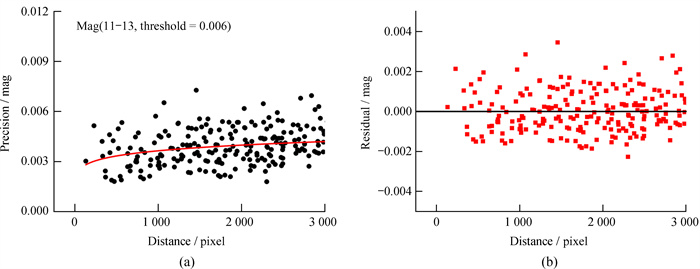
| 图 4 (a) 2021年1月15日观测资料(高度角为43°~50°,仪器星等为11~13 mag)测光精度与相对距离之间的关系,其中剔除阈值设置为0.006;(b)使用幂函数拟合后的残差随相对像素距离之间的分布情况 Fig. 4 (a) The relationship between the relative distance and photometric precision of the observations on Jan. 15, 2021 (the altitude is 43-50 deg and instrumental magnitude is 11-13 mag), in which the elimination threshold is set to 0.006; (b) the distribution of the residual fitted by power function |
|
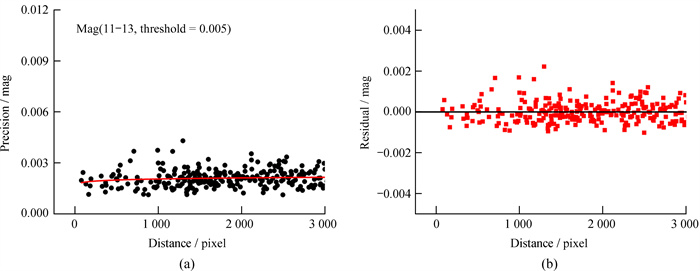
| 图 5 (a) 2021年1月15日观测资料(高度角为78°~83°,仪器星等为11~13 mag)测光精度与相对距离之间的关系,其中剔除阈值设置为0.005;(b)使用幂函数拟合后的残差随相对像素距离之间的分布情况 Fig. 5 (a) The relationship between the relative distance and photometric precision of the observations on Jan. 15, 2021 (the altitude is 78-83 deg and instrumental magnitude is 11-13 mag), in which the elimination threshold is set to 0.005; (b) the distribution of the residual fitted by power function |
从上述结果我们可以发现,同一天的测光精度,目标的高度角越大,相对测光的精度越高。在天顶附近时,亮于13 mag的恒星测光精度可达0.002 mag。当目标高度角较小时,相对测光的精度较低,且存在比较明显的测光精度回报现象。从图 3可以看出,相对测光的精度随相对像素距离的增加而降低,测光精度从0.003 mag降低到0.006 mag。
2.3 精度回报现象讨论星光经过不同质量的大气时受到的消光效应不同。因为相对角距离较小的两颗星经过大气的质量相似,所以相对测光时存在精度回报现象。当目标高度角较低时,大气质量较大,相对测光的精度回报现象较为明显。
在地面观测中,我们通常选择天顶附近的目标进行观测,以减小大气消光的影响。然而,有些目标经过子午线时高度角较低,此时使用相近的参考星进行相对测光效果较好。当天顶方向的大气质量较大时,可能也存在较为明显的精度回报现象,使用相近的恒星作为参考星进行相对测光也许是一种较好的补偿方法。测光存在精度回报现象,我们应该尽可能寻找附近的孤立亮星作为参考星,当然也需要保证参考星的光度是稳定的。
3 总结与展望本文介绍了现有的测光工具与技术,提出了把MaxIm DL与Python编程语言中photutils库函数相结合的测光技术。通过该技术,我们能够方便地处理由于星像半高全宽有较大变化时部分图像目标不能检测的问题,也能够快速进行星像测光数据的匹配和统计。通过分析1 m光学望远镜在不同高度角拍摄的M35星团图像发现,在目标高度角较低时有较明显的测光精度回报现象。在后续的工作中,我们将结合位置测量和光度测量的精度回报现象,进一步探究天体光度和位置变化的关系。
| [1] | DEVOGELE M, TANGA P, BENDJOYA P, et al. Shape and spin determination of Barbarian asteroids[J]. Astronomy&Astrophysics, 2017, 607: A119. |
| [2] | VERBISCERL A J, PORTER S, BENECCHI S D, et al. Phase curves from the Kuiper Belt: photometric properties of distant Kuiper Belt Objects observed by New Horizons[J]. The Astronomical Journal, 2019, 158(3): 123. DOI: 10.3847/1538-3881/ab3211 |
| [3] |
吴月承, 张皓晶, 余莲, 等. 平谱射电类星体3C 454.3的中长周期光变特性研究[J]. 天文研究与技术, 2020, 17(1): 1–7 WU Y C, ZHANG H J, YU L, et al. The medium and long period light variation characteristics of FSRQ 3C 454.3[J]. Astronomical Research&Technology, 2020, 17(1): 1–7. DOI: 10.3969/j.issn.1672-7673.2020.01.001 |
| [4] | LANDOLT A U. UBVRI photometric standard stars around the celestial equator: updates and additions[J]. The Astronomical Journal, 2009, 137(5): 4186–4269. DOI: 10.1088/0004-6256/137/5/4186 |
| [5] | PASCU D. An appraisal of the USNO program of photographic astrometry of bright planetary satellites[C]//Proceedings of the Royal Greenwich Observatory and the Institute of Astronomy Workshop. 1994: 304-311. |
| [6] | MORGADO B, ASSAFIN M, VIEIRA-MARTINS R, et al. Astrometry of mutual approximations between naturalsatellites. Application to the Galilean moons[J]. Monthly Notices of the Royal Astronomical Society, 2016, 460(4): 4086–4097. DOI: 10.1093/mnras/stw1244 |
| [7] | LIN F R, PENG J H, ZHENG Z J, et al. Characterization of the precision premium in astrometry[J]. Monthly Notices of the Royal Astronomical Society, 2019, 490(3): 4382–4387. DOI: 10.1093/mnras/stz2871 |
| [8] | LAHER R R, GORJIAN V, REBULL L M, et al. Aperture photometry tool[J]. Publications of the Astronomical Society of the Pacific, 2012, 124: 737–763. |
| [9] |
郭碧峰, 彭青玉, 林孚荣. Astrometrica与MaxIm DL在天体测量的应用与技术研究[J]. 天文研究与技术, 2021, 18(2): 195–202 GUO B F, PENG Q Y, LIN F R. Applications and technology research for Astrometrica and MaxIm DL in Astrometry[J]. Astronomical Research&Technology, 2021, 18(2): 195–202. |
| [10] | DA COSTA G S. Basic photometry techniques[C]//Proceedings of the ASP Conference Series. 1992: 90-104. |


