为了研究高度动态的太阳日冕结构，人们一直在提高时空分辨率方面不断探索。由于太阳日冕结构的密度、位置和形状几秒钟就会发生变化，较大的动态范围造成经过望远镜成像的日冕结构边缘模糊且噪声较大，图像可视化困难。目前有几种较为有效的增强图像算法用于太阳日冕图像增强。基于直方图均衡的方法可以利用不同分布直方图对不同图像规定化处理^[1]，也可以高斯滤波后，再独立均衡各个分区，如保持亮度的动态直方图均衡化^[2](Brightness Preserving Dynamic Histogram Equalization, BPDHE)，这些方法能够有效提高图像整体的对比度。但由于直方图的邻域通常是正方形，导致严重的伪影，从而影响日冕环状结构；其次会放大图像的低对比度噪声，图像细节模糊；亮度不同的区域之间也会失去有效结构。基于曝光融合框架的对比度增强算法^[3](Exposure Fusion Framework, EFF)可以解决直方图均衡出现的对比度过高或过低的问题。基于多种经典图像增强算法融合的方法^[4](Multi-deviation Fusion method, MF)对多种图像增强算法取长补短，图像增强时能够兼顾细节增强、对比度提高和主观感知效果等。这些方法的预处理大多采用对数变换，能够降低计算复杂度。但由于对数变换抑制了亮区梯度幅度的变化，可能导致某些区域的精细结构细节丢失。为解决这个问题，基于Retinex的方法在压缩动态范围的同时，增强边缘并保持颜色稳定，其中基于Retinex对噪声鲁棒的方法(Robust Retinex Model, rR)^[5]可提高对噪声的鲁棒性，使用一种基于拉格朗日乘子的交替方向最小化算法代替对数变换，有效解决模型优化过程中的问题，能有效保持细节结构和边缘稳定。上述方法都仅为太阳日冕图像提供了一种可视化方法，对于其中因为日冕动态变化、望远镜抖动、CCD欠采样以及杂散光等因素造成的精细结构模糊问题，无法有效增强。随着数字图像处理技术的发展，盲退卷积算法为恢复精细结构的准确性和真实性提供了科学的理论依据。文[6]根据望远镜设计理论估计满足大气成像仪不同波段的点扩散函数用于退卷积，但造成图像模糊的原因除传感器设备外，还有太阳活动位移、形状变化等，所以理论估计的点扩散函数并不能很好地退卷积得出清晰图像。在使用空间望远镜大气成像仪观测太阳日冕结构时，对由于日冕位移、形状改变、CCD欠采样以及杂散光等因素造成成像模糊，可以建模为

$ \mathit{B}{\rm{(}}\mathit{x}{\rm{) = }}\mathit{I}{\rm{(}}\mathit{x}{\rm{) * }}\mathit{k}{\rm{(}}\mathit{x}{\rm{) + }}\mathit{n}{\rm{(}}\mathit{x}{\rm{)}},\ $

(1)

其中，*表示卷积运算；B(x)表示获得的模糊图像，即大气成像仪图像；I(x)表示潜在的清晰图像；k(x)表示未知的点扩散函数；n(x)表示在每个像素x=(x, y)处相同且独立分布的噪声项。

根据求解方法的不同，盲退卷积算法大致可以分为两类：(1)通过引入额外约束条件同时对目标图像和点扩散函数估计进行交替迭代，并基于最大后验概率估计(Maximum A Posterior, MAP)完成盲退卷积的算法；(2)先估计模糊核，再退卷积得到清晰图像。第1类方法对噪声有一定的抑制作用，但涉及目标图像和点扩散函数估计的多次迭代计算，非常耗时，且严重依赖于清晰图像和点扩散函数的先验特性。对于大气成像仪图像而言，很难获得清晰图像的统计先验信息。第2类方法以基于显著性边缘^[7]和功率谱的方法^[8-9]为主，基于边缘的方法是从原图显著边缘估计模糊核，这类方法很大程度上取决于边缘选择，更适用于运动模糊估计。大气成像仪图像结构模糊，无法较好地选择边缘。基于功率谱的方法直接从输入图像功率谱中恢复点扩散函数的功率谱，再使用相位提取算法求解点扩散函数的相位。

因此，本文研究了一种利用模糊图像功率谱估计点扩散函数的单帧图像盲退卷积算法，用于太阳大气成像仪图像增强。首先对数据预处理(包括去噪和灰度值变换处理)，从图像中估计点扩散函数的功率谱；再用相位提取算法恢复点扩散函数，为了使算法对噪声更鲁棒，额外引入了权重参数α，限制使用点扩散函数功率谱对相位估计的硬性约束，并对算法随机初始化求解多次，避免陷入局部极小值。计算点扩散函数所有可能解之间的L₂范数距离，通过多次随机初始化计算点扩散函数，如果可能解之间的L₂距离越小，可以认为是最接近真解的点扩散函数，最后对(1)式利用点扩散函数退卷积得出目标图像。为进一步减少噪声影响，将待增强图像分隔为4幅相邻局部子图，并按上述方法估计每幅子图的点扩散函数，对4个点扩散函数进行归一化和求取均值得到整幅图像的点扩散函数。实验分析使用轮廓切片曲线、功率谱分析、点扩散函数分析以及和其他较为先进的增强算法结果对比分析，对重建的目标图像细节结构进行客观评价，将高分辨率日冕成像仪(The High-Resolution Coronal Imager, Hi-C)图像功率谱假设模型验证和精细结构增强效果对比。结果显示本文方法对大气成像仪19.3 nm，21.1 nm和17.1 nm波段图像的增强和复原有较好的效果，且对噪声鲁棒。此外，由于该方法不涉及目标像的反复重建，在图像恢复速度上也有一定的优势。

1 太阳动力学天文台/大气成像仪数据

太阳动力学天文台/大气成像仪^[10]主要目标是了解太阳能量存储与释放机制，确定太阳如何以及为何发生变化。通过研究太阳周围等离子体的相互作用，增强我们对太阳如何影响地球大气和社会生产的理解。大气成像仪于2010年2月11日正式启动，由4台望远镜组成，可同时提供10个波段的全日面像，包括7个极紫外波段(9.4 nm，13.1 nm，17.1 nm，19.3 nm，21.1 nm，30.4 nm和33.5 nm)、2个紫外波段(160 nm和170 nm)和1个可见光波段(450 nm)；观测范围包括太阳过渡区和最高可达0.5R_⊙的日冕，空间分辨率为1.5″，时间分辨率为12 s，视场达到41 × 41′。

高分辨率日冕成像仪^[11-12]提供了日冕更精细结构视角，获得高空间分辨率(≈0.3~0.4″)，高时间分辨率(≈5 s)的太阳活动区域结构图像，是目前为止可获得最高分辨率的太阳日冕仪，为了解小尺度日冕特征和发生在过渡区的活动现象，以及它们之间可能存在的相互关系提供依据。

由表 1数据对比可知，高分辨率日冕成像仪虽然拥有更高的时空分辨率，但视场小，拍摄时长较短，无法对日冕进行长期稳定的观测。相比而言，大气成像仪能够提供大视场、长期全日面观测图像，然而图像质量低于高分辨率日冕成像仪，因此对大气成像仪图像增强处理显得尤为重要。

本文采用的大气成像仪数据是2012年7月11日18时53分32秒可以观察到热耀斑的等离子体和日冕19.3 nm波段的局部像，和2014年2月2日23时40分11秒观测活动区日冕21.1 nm波段的局部像，这两组数据由同一望远镜拍摄。此外，实验中还包括2014年10月4日10时13分11秒不同望远镜拍摄的宁静区日冕17.1 nm波段的局部像。其中19.3 nm图像实验中，也采用了活动区域11520的2012年7月11日18时53分27秒高分辨率日冕成像仪图像作为清晰图像功率谱假设验证和实验对比，除此之外，实验对比图还包括文[6]估计的点扩散函数退卷积图。数据预处理包括：根据大气成像仪数据高动态的特点，对图像对数变换，这一步能够有效降低图像的动态范围；然后使用中值滤波对图像去噪，该算法在去除部分噪声的同时不会平滑过渡，能有效保持图像的结构。

2 盲退卷积算法理论

本文方法分为3部分：自然图像功率谱假设模型、高分辨率日冕成像仪功率谱分析和大气成像仪图像点扩散函数求解。

2.1 自然图像功率谱假设模型

文[8]的研究表明，清晰图像的功率谱(或自相关)是各向同性的，模糊过程中图像的中高频分量降低，模糊图像不同方向微分滤波后再计算自相关，当模糊方向与微分方向一致时，损失最大，此时能量绝对值之和最小的方向为模糊方向。根据以上结论，我们对清晰图像和模糊图像分别进行不同角度(θ: 1~180°)的傅里叶中心投影变换，得到不同投影角度对应的一维切片后，再对这些切片一维微分滤波, 最后计算其自相关得到

$ \left( {{\Re _{d*{P_\mathit{\theta }}(I)}}} \right)(x) \approx {c_\mathit{\theta }} \cdot \mathit{\delta }(x),\ $

(2)

$ \left( {{\Re _{d*{P_\mathit{\theta }}(B)}}} \right)(x) \approx {c_\mathit{\theta }} \cdot {\Re _{{P_\mathit{\theta }}(k)}}(x),\ $

(3)

其中，d为一维微分滤波器；c_θ为一个随角度变化的乘性因子；$\mathbb{R}$为对图像的自相关计算；Ρ为投影算子；δ为冲激函数，即

$ \mathit{\delta } = \left\{ {\begin{array}{*{20}{c}} 1&{(x,y) = (0,0)}\\ 0&{\mathit{ otherwise }} \end{array}} \right\}.\ $

(4)

2.2 高分辨率日冕成像仪图像功率谱分析

高分辨率日冕成像仪图像的功率谱特性分析如图 1。将图 1(a)的一个局部子图的R_d*Ρθ(I)绘制得到图 1(b)，图 1(b)45°，90°，135°和180°方向功率谱截面得到图 1(c)，将图 1(c)中4条曲线对应数值相除得到图 1(d)。通过观察图 1(c)，清晰图像图 1(a)经过(2)式计算得到的功率谱并不是一个精确的δ函数。由图 1(d)可以看出，不同角度的功率谱相除得到不同常数，c_θ随着投影角度的变化而变化，即太阳清晰图像功率谱随着θ不同有不同乘性因子的变化量。进而证明(2)式和(3)式用于大气成像仪图像点扩散函数估计是可靠的。图中多个尖峰是由于除数存在0值造成的。

为了不增加图像的总能量，滤波器d均值为0，在进行d*Ρ_θ(B)计算时，会导致Ρ_θ(B)的均值缺失(为0)，但图像本身功率谱并非为0，所以在计算过程中，引入参数m_θ代替0值。即$\mathfrak{R}$_Ρθ(k)(x)的均值使用m_θ/c_θ代替。令f_θ(x)=$\mathfrak{R}$_d*Ρθ(B)(x)，由(3)式可以得到

$ {\Re _{{P_\mathit{\theta }}(k)}}(x) = \left[ {{f_\mathit{\theta }}(x) + {m_\mathit{\theta }}} \right]/{c_\mathit{\theta }}.\ $

(5)

2.3 点扩散函数估计

(5) 式是一个欠定方程，为了成功恢复$\mathfrak{R}$_Ρθ(k)(x)，需要引入额外约束条件估计c_θ和m_θ。

2.3.1 估计c_θ

我们采用关于点扩散函数的3个假设^[13]对(5)式进行等价计算：

(1) 相机曝光，光子在传感器上累积图像，由于光子能量非负，故点扩散函数是非负的，即k≥0，所以关于k的投影Ρ_θ(k)和自相关$\mathfrak{R}$_Ρθ(k)都是非负的，根据(5)式可以得到f_θ(x)+m_θ≥0。

(2) 相机曝光时移动受限，故模糊过程有限，k支持域紧凑，所以对于每个角度投影的自相关$\mathfrak{R}$_Ρθ(k)来说，都存在一个s_θ使得${\Re _{{P_\mathit{\theta }}(k)}}(x) = \left\{ {\begin{array}{*{20}{c}} {\frac{{{f_\mathit{\theta }}(x) + {m_\mathit{\theta }}}}{{{c_\mathit{\theta }}}}}&{|x| < {s_\mathit{\theta }}}\\ 0&{\mathit{ otherwise }} \end{array}} \right\} $，故m_θ满足m_θ=-f_θ(s_θ)。

(3) 理论上，模糊不会影响光子达到传感器的总量，所以可以认为$\int k (x){\rm{d}}x = 1 $，也意味着$\int {{\Re _{{P_\mathit{\theta }}(k)}}(x){\rm{d}}\mathit{x}} = 1 $。根据(5)式得到${c_\mathit{\theta }} = \int {\left[ {{f_\mathit{\theta }}(x) + {m_\mathit{\theta }}} \right]} {\rm{d}}x $(即是对模糊核k归一化)。

综上，(5)式可以等价于

$ {\Re _{{P_\mathit{\theta }}(k)}}(x) = \frac{{{f_\mathit{\theta }}(x) - {f_\mathit{\theta }}\left( {{s_\mathit{\theta }}} \right)}}{{\int {\left[ {{f_\mathit{\theta }}(x) + {m_\mathit{\theta }}} \right]} {\rm{d}}x}} = \frac{{{f_\mathit{\theta }}(x) - {f_\mathit{\theta }}\left( {{s_\mathit{\theta }}} \right)}}{{\int {\left[ {{f_\mathit{\theta }}(x) - {f_\mathit{\theta }}\left( {{s_\mathit{\theta }}} \right)} \right]} {\rm{d}}x}}.\ $

(6)

2.3.2 估计支持范围s_θ

通过在点扩散函数估计和s_θ估计之间进行最大期望(Expectation-maximization, EM)迭代，从而估计s_θ和点扩散函数。最大期望算法的每次迭代是对点扩散函数的再一次修正，能够更准确估计点扩散函数，使其在盲复原工作中有效抑制振铃和伪影。具体步骤为

(1) 首先初始化s_θ⁽⁰⁾=arg min_xf_θ(x)，之后每次更新为s_θ⁽ⁱ⁾；

(2) 使用s_θ⁽ⁱ⁾估计R_Ρθ(k)⁽ⁱ⁾(x)，再根据相位提取算法(算法2)迭代当前满足最大期望值的k⁽ⁱ⁾；

(3) 根据第2步的k⁽ⁱ⁾更新s_θ⁽ⁱ⁺¹⁾，用于第i+1次迭代；

(4) 2，3两步反复迭代直到满足条件s_θ⁽ⁱ⁺¹⁾>0.1max($\mathfrak{R}$_Ρθ(k))时停止迭代。

图 2(a)为支持域s_θ迭代路径，图 2(b)为根据最终s_θ迭代结果恢复的点扩散函数功率谱。图 2(a)中蓝色曲线表示初始化的s_θ，根据最大期望迭代更新s_θ(红色曲线)，达到终止条件后s_θ(绿色曲线)的数值用于作为图 2(b)图横轴的支持域数值。

算法1(求解k)的步骤可归纳为

输入：模糊图像B；

输出：$k = \left( {\sum\limits_{t = 1}^T {{k_t}} } \right)/T$。

(1) f_θ(x)=$\mathfrak{R}$_d*Ρθ(B)。

(2) 初始化s_θ⁽⁰⁾=arg min_xf_θ(x)。

(3) 外循环开始，令次数t=1。

(4) 内循环开始：

    ①使用给定的s_θ，根据(6)式计算模糊核功率谱${\left| {\hat k} \right|^2} $(^ 表示对信号做傅里叶变换)；

    ②通过算法2计算模糊核k_t；

    ③最大期望迭代更新s_θ。

(5) 当满足s_θ＞0.1max($\mathfrak{R}$_Ρθ(k))时内循环结束。

(6) t=T_outer(T表示剪切图像张数)时外循环结束。

图 3是本文算法流程，首先对原图(a)去噪和对数变化得到图 3(b)，计算图 3(b)的一维自相关图 3(c)，根据图 3(c)迭代支持域s_θ图 3(d)，最后使用该s_θ校准点扩散函数一维功率谱图 3(e)，复原为二维功率谱图 3(f)，相位提取算法计算相位后恢复点扩散函数图 3(g)，最后非盲退卷积得到目标图像图 3(h)。

2.4 点扩散函数的相位恢复

求出${\left| {\hat k} \right|^2} $之后，我们使用相位提取算法，通过添加约束条件求解模糊核k的相位分量φ(ω)，最终得到模糊核k。相位提取算法是一种欠定算法，该算法的解存在平凡模糊的问题，通常会收敛到平凡解或局部极小值。典型的相位恢复方法以误差下降算法(Error-Reduction, ER)为例，在迭代过程中降低误差，但将不满足约束的信号设为0值的方式常常使迭代停滞，混合输入输出(Hybrid Input-Output, HIO)算法^[14]改进了此问题，对解设置一个小扰动，可以使迭代跳出停滞现象快速收敛。文[15]提出松弛平均交替反射(Relaxed Averaged Alternating Reflection, RAAR)算法，该方法能够使收敛更快更平稳，但将输入的功率谱作为一种硬性约束，即需要恢复的信号完全满足输入的功率谱，当输入信号含有噪声时，会使收敛震荡，鲁棒性欠佳。大气成像仪图像噪声复杂，并不能在数据预处理阶段完全消除，故本文算法放宽了模糊核功率谱的硬性约束要求(通过调整权重参数α)，可提高算法对噪声的鲁棒性。初始阶段采用随机初始化相位分量，多次重复此随机过程，可以避免收敛到局部极小值；其次，引入混合输入输出算法对解的扰动方法(即算法2中β项)，可以使解快速收敛。最后计算所有可能解的L₂距离，求出最优解。

算法2(求解k_t)迭代包括以下步骤：

输入：ρ(ω)= $\left| {\hat k(\mathit{\omega })} \right| $，点扩散函数尺寸s；

输出：k_t。

(1) 外循环n=1：

① 随机初始化相位φ(ω)([-π, π]之间)；

② 计算$\mathbb{G}$=$\mathcal{F}$^-1(ρe^iφ(ω))；

③ 内循环m=1：

    (a) 施加傅里叶域约束(即是对幅值ρ放宽至α倍)：

$ {\mathbb{G}_2} = {\mathcal{F}^{ - 1}}\left\{ {[\mathit{\alpha \rho } + (1 - \mathit{\alpha })|\hat {\mathbb{G}}|]{{\rm{e}}^{{\rm{i}} \cdot \mathit{\varphi }\hat {\mathbb{G}}}}} \right\}; $

    (b) 施加空间域约束(即点扩散函数非负性约束和支持域约束)：

$ \mathbb{G}(x) = \left\{ {\begin{array}{*{20}{c}} {\mathit{\beta \; \mathbb{G}}(x) + (1 - 2\mathit{\beta }){\mathbb{G}_2}(x)}&{x \in \mathit{\Omega }}\\ {{\mathbb{G}_2}(x)}&{z \notin \mathit{\Omega }} \end{array}} \right\} $

(7)

其中，Ω={x: 2g₂(x)-g(x) < 0}∪{x: x∉[0, s]×[0, s]}，为使m次迭代中，信号能够平稳快速地收敛，本文采用混合输入输出算法中对β的设置，即β=β₀+(1-β₀)[1-e^(-m/7)3]。本实验中β₀=0.75，当出现x∈Ω时，为$\mathbb{G}$赋予一个较小的值β$\mathbb{G}$(x)+(1-2β)$\mathbb{G} $₂(x)，以便能够逃出迭代过程中的停滞现象；

④ m=M_outer时，内循环结束；

⑤ 复原${k_{\rm{n}}}(x) = \left\{ {\begin{array}{*{20}{c}} {{\mathbb{G}_2}(x)}&{x \notin \mathit{\Omega }}\\ 0&{x \in \mathit{\Omega }} \end{array}} \right\} $，其中Ω={x: $\mathbb{G}$₂(x) < 0}∪{x: x∉[0, s]×[0, s]}。

(2) n=N_outer时，外循环结束，k_n两两计算L₂距离，得到最优解k_t。

算法2包括两个循环结构，设置外循环为了避免解陷入局部极小值，初始化值越接近真值，越容易收敛到全局最小值。多次相位随机初始化求解k(x)，最终通过求不同解之间的范数距离，范数距离最小的解可认为是最优解k(x)。设置内循环能够使算法平稳快速地收敛，在迭代求解过程中交替引入频域约束(幅值约束)和空间域约束(点扩散函数的非负性约束和支持域约束)，当出现x∈Ω时，为$\mathbb{G}$赋予一个较小的值β $\mathbb{G}$(x)+(1-2β)$\mathbb{G}$₂(x)，以便能够避免迭代过程中的停滞现象。文[15]指出，通过逐步增大β值能够引导解稳定收敛。故本文通过内循环将β值设置为一个不断接近1的动态值。

如(1)式，已知模糊核k(x)和模糊图像B(x)，求解目标清晰图像的方法叫作非盲退卷积算法。实验使用文[16]中交替最小化的方法，即半二次分裂方法来求解目标图像I(x)。

3 实验结果分析

为了评估该方法的有效性和准确性，本文实验中对大气成像仪19.3 nm，21.1 nm和17.1 nm 3个波段不同区域进行增强，图像均通过对数显示。图 4中3个波段的图像在增强后，细节结构更锐，尤其冕环之间的相对模糊结构增强后能较好地分离，边界更为清晰。由第3列本文算法估计的点扩散函数尺寸大小可知，19.3 nm和21.1 nm波段点扩散函数较17.1 nm更大，这说明前两个波段图像模糊程度更高，由于19.3 nm和21.1 nm波段的图像主要是拍摄太阳活动区得到的，活动区更大的动态范围和冕环相对望远镜的运动造成图像模糊程度更高。在第4列功率谱图中，3个波段图像增强后的功率谱曲线相对大气成像仪图像曲线在中频都有一定程度的提高。中频曲线的提高在增强图像中表现为已有结构边界更锐，以及由于模糊没观察到的细节结构也得以恢复。

为了更好地对比细节结构的增强情况，我们在图 5中引入结构的轮廓切片图。文[6]根据大气成像仪的成像特点估计不同波段点扩散函数用于增强图像，太阳一个波段的所有图像使用同一个点扩散函数退卷积得到，这是不准确的，图像模糊原因也只考虑望远镜设备的因素，所以恢复结果不佳(如图 5第2列)。图 5中，我们对不同波段不同的区域分别增强，并将本文估计的点扩散函数与文[6]点扩散函数作对比。如19.3 nm波段的两幅局部图，本文估计的点扩散函数尺寸相当，但形状不同，对于结构A和结构B，冕环能较好地分离，如轮廓切片图所示。同样，在21.1 nm和17.1 nm波段的增强图中，C，D和E结构的模糊方向与点扩散函数形状一致，不同的区域，太阳活动不一致，冕环位置和形状的变化，相互干扰是不可控的。这也是必须分区域单独估计点扩散函数退卷积图像的原因。

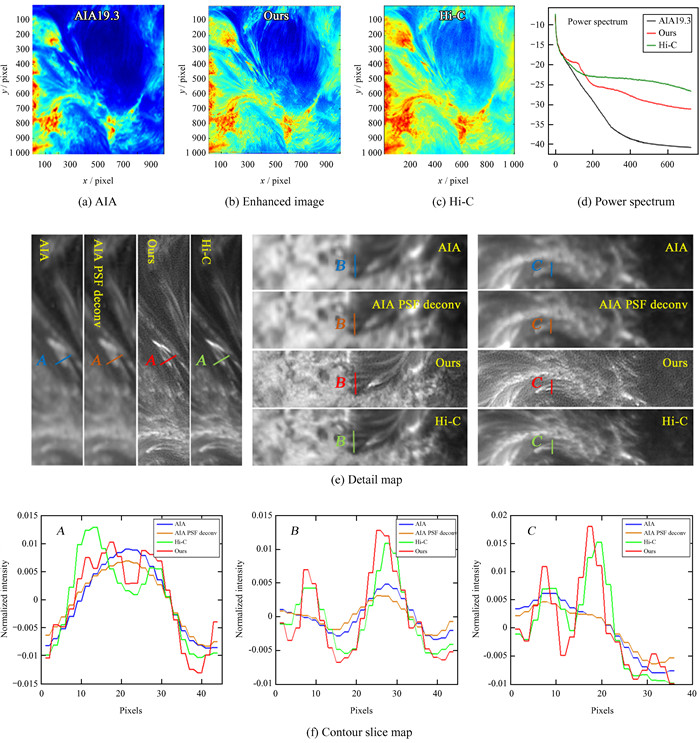
如图 6，通过引入更高分辨率的日冕成像仪图像进行细节结构对比，评估本文增强方法的准确性。为了便于与高分辨率日冕成像仪图对比，图 6(a)，(b)经过放大和对数处理。观察三者的能量图可知，大气成像仪图像细节区域颜色相近，模糊明显，几乎看不到细节结构，增强后的图像与高分辨率日冕成像仪图像相近。通过三者的功率谱图图 6(d)可以看出，大气成像仪几乎没有高频细节，中频部分也很弱。经过本文方法增强后的图像，中高频都有一定的提高，略弱于高分辨率日冕成像仪图像，说明恢复细节结构的数量少于高分辨率日冕成像仪图像，中频处有一点略高于高分辨率日冕成像仪图像。在细节图 6(e)中可观察到，本文方法不仅能较好地分离冕环的相对模糊结构，且对于已存在的冕环，能更好地保持边缘。细节结构边缘较高分辨率日冕成像仪尖锐，所以中频曲线略高于高分辨率日冕成像仪。图中的A，B和C都是由于模糊无法分辨的结构，增强后，与高分辨率日冕成像仪对比可知，结构保持稳定，且恢复情况较为准确。如对应的轮廓切片图 6(f)A结构，大气成像仪中表现为一个冕环的结构，成功地分离为两条冕环，与高分辨率日冕成像仪保持一致。

图 7给出了经典的基于直方图的BPDHE算法，以及目前较为先进的EFF，MF和rR算法的实验结果。从第1行局部放大细节中可以看出，BPDHE方法使图像局部过度增强且细节模糊，本文算法的增强图对细节增强效果更好，边缘结构也较为稳定。第2行为各个算法对应的直方图，根据直方图像素值的分布情况可以看出，MF算法的可视化效果最好。对比其他增强算法，本文算法在保证对比度和亮度增强的同时，能复原更精细的细节结构。如表 2，我们对不同算法分别计算了标准差和信息熵，这两者可以有效地反映图像的对比度和亮度信息，其值越大，表示图像信息丰富。亮度误差^[4](Lightness Order Error, LOE)能够衡量图像的亮度失真情况，值越小代表亮度越好。结构相似度(Structural Similarity, SSIM)可以用来衡量图像恢复质量，是图像亮度、对比度和结构对比三者评估的指标，其值越接近1，图像质量越好。表中的方法均与高分辨率日冕成像仪图像作对比计算结构相似度。相比而言，虽然本文算法运行时间较长，但对细节结构的增强更为准确。

4 结论

本文提出了一种基于盲退卷积的太阳大气成像仪图像质量增强方法，基于图像功率谱特性的点扩散函数估计模型，从大气成像仪图像中估计点扩散函数，最后退卷积得出增强图像。文中采用轮廓切片分析评估方法的准确性，功率谱分析评估方法的有效性，不同区域点扩散函数分析评估方法的合理性。实验结果表明，本文方法对大气成像仪19.3 nm，17.1 nm和21.1 nm波段图像增强效果较好，尤其纹理细节和边缘结构的增强效果最好。其次，本文算法也有一定的噪声抑制效果，得益于点扩散函数相位估计过程的松弛设计，恢复新细节结构也较为准确，因为这三个波段的图像噪声较小，日冕结构特征也更丰富和明显，能够更为准确地估计模糊核。对比其他图像增强方法，本文方法的实时性较差，点扩散函数估计和退卷积的最优化迭代过程是主要的耗时原因。将来可以通过提高计算设备的性能和采用较为快速且有效的最优化方法来提高算法的实时性。在大气成像仪的其他波段图像中，9.4 nm，13.1 nm和33.5 nm波段图像噪声很大，异常点较多，结构相对模糊导致增强效果不佳，将来能够通过研究更好的去噪算法和对噪声更加鲁棒的退卷积算法对其他波段的图像进行有效增强。