2. 中国科学院自适应光学重点实验室, 四川 成都 610209;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Adaptive Optics, Chinese Academy of Sciences, Chengdu 610209, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
太阳大气的局部区域存在多种不同的活动现象,包括太阳黑子、日冕物质抛射、耀斑爆发等。这些太阳活动作用于日地空间环境,对地球气候、人类健康、电子电力设备、无线电通讯以及航空飞行器等有重大影响[1]。通过研究太阳活动实现对灾害性空间天气的有效预报,是当今太阳物理学研究的一项重要课题。太阳磁场是太阳活动的根本驱动力,而太阳磁场的测量通常采用对特定磁敏感谱线的偏振测量实现。太阳谱线在磁场中发生分裂,裂距和支线偏振态与磁场强度和方向呈现一定的函数关系,通过精确测量太阳光的偏振状态,建立偏振辐射转移方程,反演太阳大气中的磁场形态,可以研究太阳黑子、耀斑及日冕物质抛射等活动现象,对日地空间环境研究、灾害性空间天气监测和预报以及太阳物理研究具有重要意义[2]。
国内外太阳磁场的观测主要通过在太阳望远镜上安装偏振测量仪器对太阳光谱偏振信息进行测量实现。地基太阳望远镜的观测受到大气湍流的影响,当望远镜放大倍率较大时,成像光斑模糊抖动,大大影响观测分辨率,并且白天大气湍流更强。当偏振测量的时间分辨率较高时,可在一定程度上达到冻结大气湍流的效果,降低大气湍流对测量精度的影响。除此之外,太阳磁场始终处于快速变化中,为了能够精确测量太阳光的偏振态,反演得到太阳大气的磁场,偏振测量仪器的时间分辨率是一个重要指标。
目前,国内太阳望远镜上使用的偏振分析器主要采用带有经典波片的调制系统。这种传统的偏振调制器也应用于国外的太阳偏振分析器,如德国格雷戈尔(Gregor) 望远镜上装载的理想光谱偏振仪(Polarimeteric Littrow Spectrometer, POLIS),波片的旋转频率为15 Hz。美国大熊湖新太阳望远镜(New Solar Telescope, NST) 的可见光偏振成像仪(Visible Imaging Magnetograph, VIM)和第2代近红外光谱偏振仪(Near Infra-Red Imaging Spectropolarimeter, NIRIS) 都采用了旋转波片调制方式。NIRIS的波片调制器连续旋转,与红外相机的帧率相结合,以22.5°步长旋转一周获得16帧图像。目前,相机能够以10帧/秒的速度完成低噪声采集,所以,NIRIS光谱-偏振测量的频率通常为10 s,其中VIM的时间分辨率为10 s左右[3-4]。国内的1 m新真空太阳望远镜(New Vacuum Solar Telescope, NVST) 一组8步式调制需要4 s左右完成,每个调制位置耗费的总时间为波片旋转到位所需要的时间与数据采集时间之和,而波片旋转消耗的时间占了很大一部分[5-6]。在此基础上,怀柔太阳观测站的35 cm太阳磁场望远镜采用波片+ DKDP晶体的调制方式。这种方式可以利用正负电压翻转控制DKDP晶体的延迟,快速采集两个参数的图像,减少波片旋转的次数,缩短调制时间[7]。但是,旋转部件增加系统的质量和体积,容易导致仪器抖动,从而降低测量精度。如果波片采用切入切出的方式,调制时间大大增加,一次切换时间一般大于5 s。这些缺点对于星载仪器更为严重,并且有机械故障的风险。相对而言,波片+ DKDP晶体的调制方式缩短了测量时间,但由于波片结构的存在,不能充分利用DKDP晶体快速调制的优点,仍然需要大量调制时间,实时性不高。DKDP晶体和液晶相位可变延迟器(Liquid Crystal Variable Retarders, LCVR) 都是通过改变偏振相位的方式实现对入射光的偏振调制,两者在材料、性能等方面存在较大区别。相比较而言,液晶相位可变延迟器调制频率在100 Hz左右,对温度敏感,光谱范围窄,稳定性相对较差,在实际应用中尚未成熟。DKDP晶体的调制频率较高,可达1 000 Hz以上,重复性好,且在多套系统中成功应用,技术成熟可靠。
根据以上背景,本文提出了基于双DKDP晶体的实时偏振测量方案。方案采用两片DKDP晶体作为偏振调制器件,通过外加电压的方式控制DKDP晶体的相位延迟变化,DKDP晶体的电压-相位延迟响应速度可以达到毫秒级[8]。这种调制方法没有任何机械运动,没有移动部件,可以提供毫秒级切换速度,再加上曝光时间短,时间分辨率可达到传统波片+ DKDP调制方式的10倍以上,使得冻结大气湍流成为可能。为了进一步验证方案的可行性,本文在方法原理、参数优化、仿真分析和测量时间等方面进行了分析和验证。
1 原理和方法光的偏振信息可以用电矢量、琼斯矢量和斯托克斯矢量表示,其中,电矢量和琼斯矢量只能表示完全偏振光,斯托克斯矢量用4个光强参量可以表示任意偏振态的光,因此本文选用斯托克斯矢量表示被测光的偏振态。斯托克斯矢量S的具体表达式为
| $ \begin{aligned} &\boldsymbol{S}=[I, Q, U, V]^{\mathrm{T}}, \\ &I=<E_{x} {E_{x}}^{*}+E_{y} {E_{y}}^{*}>{E_{x}}^{2}+{E_{y}}^{2}, \\ &Q=<E_{x} {E_{x}}^{*}-E_{y} {E_{y}}^{*}>{E_{x}}^{2}-{E_{y}}^{2}, \\ &U=<E_{x} {E_{y}}^{*}+E_{y} {E_{x}}^{*}>=2 E_{x} E_{y} \cos \delta, \\ &V=-i<E_{x} E_{y}{ }^{*}+E_{y} {E_{x}}^{*}>=2 E_{x} E_{y} \sin \delta. \end{aligned} $ | (1) |
其中,*为复共轭;δ=φy-φx,为x与y分量的相位差;I为光波的总光强;Q为光分解到x,y方向后,x与y分量光强的差值;U为光分解到45°和135°方向后两分量光强的差值;Q和U代表光波的线偏振特性;V为光分解为右旋和左旋分量后两分量光强的差值,V代表光波的圆偏振特性。
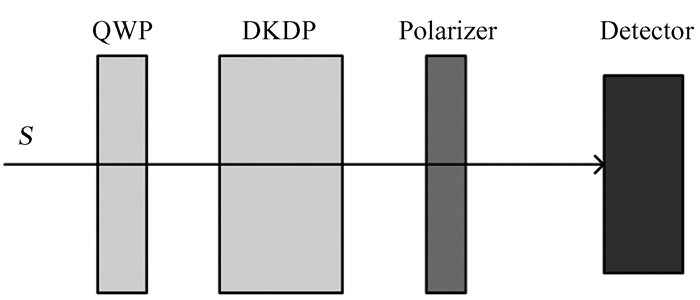
1.1 传统波片与DKDP晶体的调制方法传统的偏振测量方案采用λ/4波片与DKDP晶体作为偏振调制器件,并且一次完整的斯托克斯矢量测量需要进行6次调制,得到6组光强值。此方案中DKDP晶体快轴角度为45°,偏振片透光轴角度为0°。传统λ/4波片+ DKDP偏振分析器示意图如图 1。
|
| 图 1 传统λ/4波片+ DKDP偏振分析器示意图 Fig. 1 Schematic diagram of traditional λ/4 wave plate + DKDP polarization analyzer |
测量纵向磁场时,λ/4波片在光路之外,在DKDP晶体上加矩形正负高压,使相位延迟在±λ/4之间调制。左右旋圆偏振光交替通过分析器,斯托克斯矢量V信号可以从右旋圆偏振光与左旋圆偏振光的差中得到。测量横向磁场时,将λ/4波片放在光路中,光轴方向角调为0°,然后在DKDP晶体外加矩形正负高压,则偏振方位角分别为0°和90°的线偏振光交替通过检偏器,它们的差值即斯托克斯矢量U信号。调整λ/4波片的光轴方位角为45°,在DKDP晶体外加矩形正负高压,偏振方位角分别为45°和135°的线偏振光交替通过,相减后得到Q信号。偏振分析器的调制参数如表 1。
| λ/4 wave plate/° | DKDP crystal/° | Polarizer/° | Measurement result |
| 45 | -90 | 0 | I1=I+Q |
| 45 | 90 | 0 | I2=I-Q |
| 0 | -90 | 0 | I3=I+U |
| 0 | 90 | 0 | I4=I-U |
| - | 90 | 0 | I5=I+V |
| - | -90 | 0 | I6=I-V |
在此方案中,λ/4波片的切换时间为秒量级,且在测量一个波长点时需要采集6帧光强图像,切换3次λ/4波片。在太阳磁场测量中,相比单波长点测量,多波长点测量可以避免饱和效应造成的非线性、多普勒位移以及法拉第(Faraday) 效应等的影响。多波长点测量一般选取谱线轮廓上6个波长点,此时,一次完整的谱线测量至少需要采集36帧光强图像,切换18次λ/4波片,测量时间长,时间分辨率低,实时性较差。
1.2 基于双DKDP晶体的调制方法当光的偏振态用斯托克斯矢量S表示时,传输介质对光偏振态的作用可以用穆勒(Mueller) 矩阵M表示。光束依次经过1,2,3,…,n个传输介质后,斯托克斯矢量为
| $ \boldsymbol{S}^{\prime}=M_{n} M_{n-1} \cdots M_{2} M_{1} S. $ | (2) |
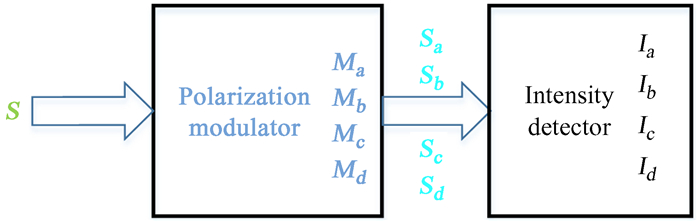
偏振测量的原理如图 2。
|
| 图 2 偏振测量原理图 Fig. 2 Polarization measurement principle diagram |
偏振测量仪通常由偏振调制器和光强探测器构成。对于斯托克斯矢量S (未知) 的待测偏振光,经过调制状态a后,斯托克斯矢量为Sa =[Ia, Qa, Ua, Va]T,此时调制状态a对应的穆勒矩阵为
| $ \boldsymbol{M}_{a}=\left[\begin{array}{llll} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{array}\right], $ | (3) |
此时
| $ \boldsymbol{S}_{a}=M_{a} \boldsymbol{S}. $ | (4) |
光强探测器只能探测到光强信息,即I满足
| $ I_{a}=a_{11} I+a_{12} Q+a_{13} U+a_{14} V. $ | (5) |
经过a,b,c和d 4组不同的调制状态后可以得到4组光强值,满足
| $ \left[\begin{array}{c} I_{a} \\ I_{b} \\ I_{c} \\ I_{d} \end{array}\right]=\left[\begin{array}{llll} a_{11} & a_{12} & a_{13} & a_{14} \\ b_{11} & b_{12} & b_{13} & a_{14} \\ c_{11} & c_{12} & c_{13} & c_{14} \\ d_{11} & d_{12} & d_{13} & d_{14} \end{array}\right]\left[\begin{array}{c} I \\ Q \\ U \\ V \end{array}\right]. $ | (6) |
将(6) 式记为Im= XS。当调制矩阵X可逆,方程有唯一解,待测光斯托克斯矢量为
| $ \boldsymbol{S}=\boldsymbol{X}^{-1} \boldsymbol{I}. $ | (7) |
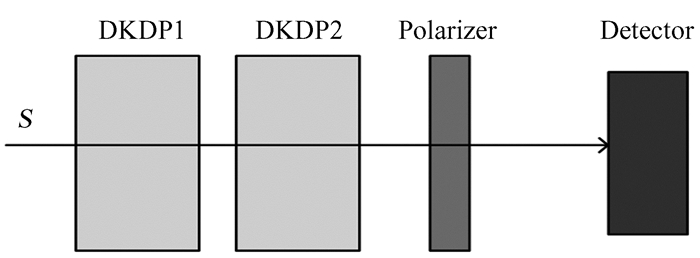
我们提出了一种基于双DKDP的偏振测量方法,如图 3。该偏振分析器的偏振调制器由两组快轴方向不同的DKDP晶体和一个偏振片构成,光强探测器为光强采集相机。假定入射光斯托克斯矢量为Sin,
| $ \boldsymbol{S}_{\text {in }}=\left[\begin{array}{l} I \\ Q \\ U \\ V \end{array}\right], $ | (8) |
|
| 图 3 基于DKDP的偏振分析器结构示意图 Fig. 3 Schematic diagram of the structure of the polarization analyzer based on DKDP |
则通过偏振调制器后的斯托克斯矢量变为Sout,
| $ \boldsymbol{S}_{\text {out }}=M_{\mathrm{p}} M_{2} M_{1} \boldsymbol{S}_{\text {in }} $ | (9) |
其中,M1,M2和Mp分别为第1组DKDP晶体、第2组DKDP晶体和检偏器的穆勒矩阵。
令DKDP1晶体快轴角度为0°,相位延迟量为δ,DKDP2晶体快轴角度为45°,相位延迟量为ε,检偏器(偏振片) 透光轴为0°。检偏器的偏振方向角与笛卡尔坐标系的选取有关,为了方便分析,我们令检偏器的偏振方向为坐标系的x轴方向。则DKDP晶体和检偏器的穆勒矩阵M1,M2,Mp为
| $ M_{1}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \cos \delta & \sin \delta \\ 0 & 0 & -\sin \delta & \cos \delta \end{array}\right], $ | (10) |
| $ M_{2}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \varepsilon & 0 & -\sin \varepsilon \\ 0 & 0 & 1 & 0 \\ 0 & \sin \varepsilon & 0 & \cos \varepsilon \end{array}\right], $ | (11) |
| $ M_{\mathrm{p}}=0.5\left[\begin{array}{llll} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]. $ | (12) |
此时,通过偏振分析器后的斯托克斯矢量为
| $ \boldsymbol{S}_{\text {out }}=\left[\begin{array}{c} I \\ Q \\ U \\ V \end{array}\right]=M_{p} M_{2} M_{1} \boldsymbol{S}_{\text {in }}, $ | (13) |
光强探测器接收到的光强为
| $ I=0.5(I+Q \cos \varepsilon+U \sin \varepsilon \sin \delta-V \sin \varepsilon \cos \delta). $ | (14) |
改变两组DKDP晶体的外加电压,得到4组不同的偏振调制状态,光强探测器测得4组不同的光强值Iout =[I1, I2, I3, I4]T。由于一般只需要斯托克斯矢量的相对值,所以(14) 式中的0.5可省略,得到偏振调制矩阵
| $ \boldsymbol{X}=\left[\begin{array}{cccc} 1 & \cos \varepsilon_{1} & \sin \varepsilon_{1} \sin \delta_{1} & -\sin \varepsilon_{1} \cos \delta_{1} \\ 1 & \cos \varepsilon_{2} & \sin \varepsilon_{2} \sin \delta_{2} & -\sin \varepsilon_{2} \cos \delta_{2} \\ 1 & \cos \varepsilon_{3} & \sin \varepsilon_{3} \sin \delta_{3} & -\sin \varepsilon_{3} \cos \delta_{3} \\ 1 & \cos \varepsilon_{4} & \sin \varepsilon_{4} \sin \delta_{4} & -\sin \varepsilon_{4} \cos \delta_{4} \end{array}\right], $ | (15) |
则有Iout=0.5 XSin。当偏振调制矩阵X可逆,可得
| $ \boldsymbol{S}_{\mathrm{in}}=\left[\begin{array}{c} I \\ Q \\ U \\ V \end{array}\right]=2 \boldsymbol{X}^{-1}\left[\begin{array}{c} I_{1} \\ I_{2} \\ I_{3} \\ I_{4} \end{array}\right], $ | (16) |
Sin即为待测光斯托克斯矢量。
2 参数最优化设计偏振测量过程中测量精度受偏振调制器调制矩阵误差和光强探测器探测误差等的影响,偏振调制矩阵参数的不同对误差的传播影响不同。在保证偏振调制矩阵可逆的同时,合理选用调制参数可以显著减小噪声扰动和系统误差对测量结果的影响。此处以假定只存在光强探测器误差为例。令I′为光强探测值,I为光强真值,S′为斯托克斯矢量计算值,S为真值。光强误差ΔI=I′-I,斯托克斯矢量误差ΔS为
| $ \Delta S=S^{\prime}-S=X^{-1} I^{\prime}-S=X^{-1}(I+\Delta I)-S=X^{-1} \Delta I, $ | (17) |
由I=XS,得
| $ \|I\|=\|X S\| \leqslant\|X\|\|S\|, $ | (18) |
| $ \|\Delta S\|=\left\|X^{-1} \Delta I\right\| \leqslant\left\|X^{-1}\right\|\|\Delta I\|, $ | (19) |
| $ \frac{\|\Delta S\|}{\|S\|} \leqslant\left\|X^{-1}\right\|\|X\| \frac{\|\Delta I\|}{\|I\|}. $ | (20) |
(20) 式给出了相对误差‖ΔS‖/ ‖S‖的上限,光强探测器误差在求解过程中可能放大‖X-1‖‖X倍。偏振调制矩阵误差结果相同,在此不做推导。我们通常称cond(X)‖‖X-1 ‖‖X‖为矩阵X的条件数(CN) [9]。矩阵X的条件数越小,在矩阵方程求解过程中误差的放大越小。根据研究结果以及仿真验证,对于全斯托克斯矢量测量,偏振调制矩阵的条件数最小值为
偏振调制矩阵如(15) 式,基于优化速度更快的拟牛顿算法,通过最小化矩阵X的条件数实现优化过程[10]。拟牛顿算法是解决无约束优化问题有效且成熟的算法,相对于牛顿算法,只要求目标函数一次连续可微,易于实现,计算量小。通常情况下,实现相同的最佳优化条件数有无限种解决方案,用于偏振测量时,它们具有相同的性能,此处我们仅选取其中一组参数(如表 2)。偏振调制矩阵为
| $ \boldsymbol{X}_{\mathrm{CN}}=\left[\begin{array}{rrrr} 1 & 0.577\ 3 & 0.577\ 4 & 0.577\ 4 \\ 1 & 0.577\ 3 & -0.577\ 4 & -0.577\ 4 \\ 1 & -0.577\ 3 & -0.577\ 4 & 0.577\ 4 \\ 1 & -0.577\ 3 & 0.577\ 4 & -0.577\ 4 \end{array}\right] $ | (21) |
| DKDP1 delay/rad | DKDP2 delay/rad | Polarizer angle/° |
| 5.497 8 | 5.327 9 | 0 |
| 5.497 8 | 0.955 3 | 0 |
| 3.927 0 | 2.186 3 | 0 |
| 3.927 0 | 4.096 9 | 0 |
时,误差的放大最小。
此外,偏振调制矩阵的等加权方差也是评估误差传递的标准之一,但等加权方差的值主要受数据冗余的影响。本文的新测量方案仅适用于带宽极窄(Δλ ≤ 0.01 nm) 的情况,通常与滤光器配合使用,光谱色散问题可以忽略,不考虑偏振测量效率。本文使用的DKDP晶体透过范围为200~2 150 nm,在目标波长532.4 nm处透过率可达97%。
3 仿真分析验证传统的波片+ DKDP晶体偏振分析器常采用6次调制的测量方案,由于冗余项的存在,精度略优于同等条件下(
测量过程中,受到环境杂散光和光强探测器本身噪声的影响,光强探测器测得的光强值存在一定的误差。此误差直接反应待测光的偏振误差,因此,我们有必要验证本文提出的测量方案的误差是否满足测量精度要求。
一般情况下,光强探测器的非线性在1%~2%,难以满足偏振测量的要求,需要对响应函数进行标定。假定光强探测器的非线性误差为δ=0.02,且只考虑光强探测器误差,光强误差导致的偏振误差为
| $ \Delta S=S^{\prime}-S=X^{-1} I^{\prime}-X^{-1} I. $ | (22) |
为了评估方案的性能,我们分析了光强噪声标准差为0.02和0.001时,1 000个不同入射偏振态(不同偏振分量) 的测量精度。一般地,光束的完全偏振态可以用庞加莱球(Poincaré Sphere) 球面上的点表示,如图 4。我们选取庞加莱球面上1 000个均匀采样点,其中20个不同椭圆度的圆从南极到北极,每个圆的50个方位角顺时针方向移动指向的偏振态作为入射偏振态,如图 5。在仿真中,通过添加一个信号独立的高斯噪声,每个状态产生100组强度值,计算100组测量误差的标准差作为对应偏振态的测量误差。

|
| 图 4 庞加莱球 Fig. 4 Poincaré Sphere |
|
| 图 5 偏振采样点 Fig. 5 Polarization sampling points |
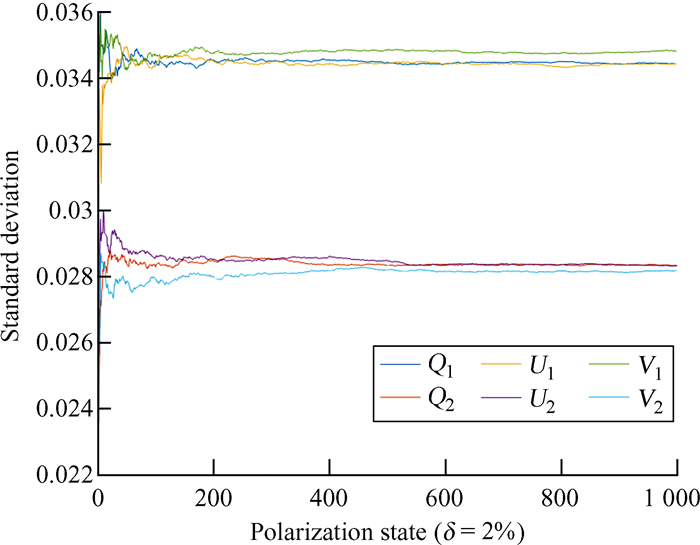
图 6中,Q1~V1为我们提出的DKDP偏振测量方案结果,Q2~V2为传统方案测量结果。显然,两种测量方案的斯托克斯矢量误差在同一数量级,但由于光强探测器非线性为2%,导致两种方案的误差都达到了10-2量级,难以满足测量要求。我们又将光强探测器的非线性降低到1‰后,得到图 7的结果。由图 7可以看到,在光强探测误差为1‰时,对于斯托克斯矢量Q,U和V分量的测量误差,传统测量方案的误差在1.4 × 10-3左右,而新的偏振测量方案误差在1.7 × 10-3左右,误差均小于2 × 10-3,满足偏振测量的要求。
|
| 图 6 斯托克斯矢量误差比较(δ=2%) Fig. 6 Stokes vector error comparison (δ=2%) |

|
| 图 7 斯托克斯矢量误差比较(δ=1‰) Fig. 7 Stokes vector error comparison (δ=1‰) |
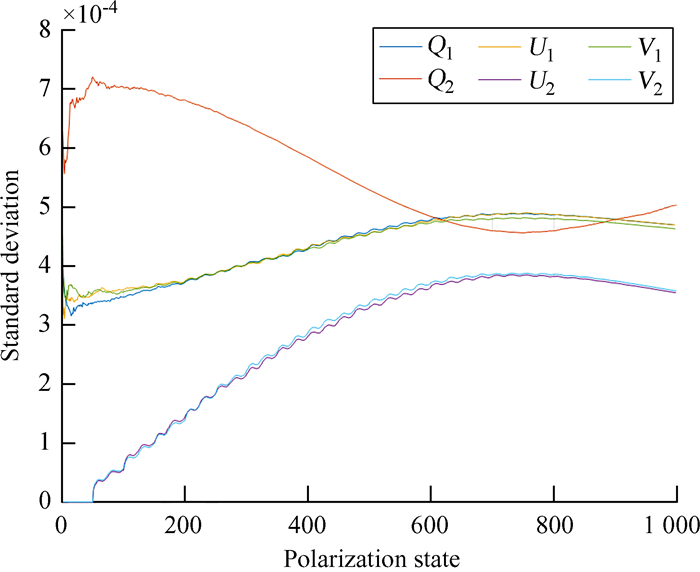
测量过程中,在控制外加电压切换DKDP晶体相位延迟时,由于电压-相位延迟曲线存在一定的误差,导致偏振测量的结果也出现误差。经过对应波长下(本文为532.4 nm) 的电压-相位延迟标定后,DKDP晶体的延迟误差一般小于0.001 rad。我们需要验证两种测量方案下,由相位延迟误差引起的偏振测量误差是否在允许范围内。被测偏振态的采样方法与上述方法相同,在仿真时,添加一个独立的标准差为0.001 rad的角度误差,得到1 000个偏振状态的测量误差。
图 8中,Q1~V1为我们提出的双DKDP偏振测量方案结果,Q2~V2为传统方案测量结果。容易看出,两种测量方式由DKDP相位延迟误差引起的偏振测量误差均小于10-3,其中,Q分量测量结果优于传统测量方式,U分量和V分量误差值几乎相等,满足测量需求。
|
| 图 8 DKDP相位延迟误差导致的测量误差比较 Fig. 8 Comparison of measurement errors caused by DKDP phase delay error |
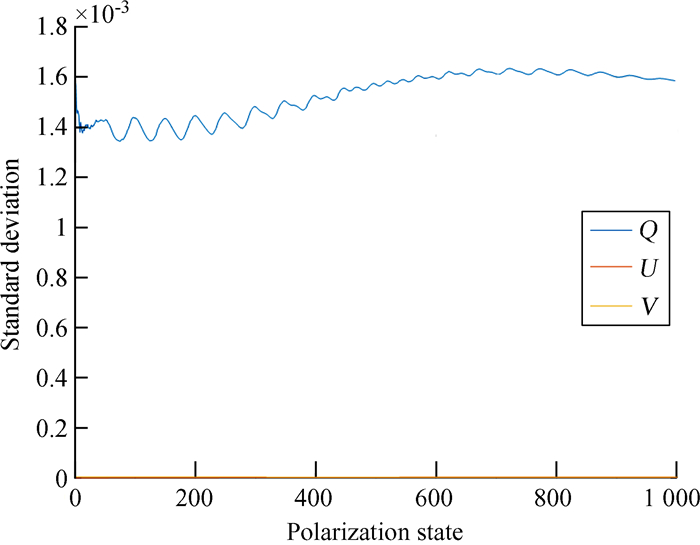
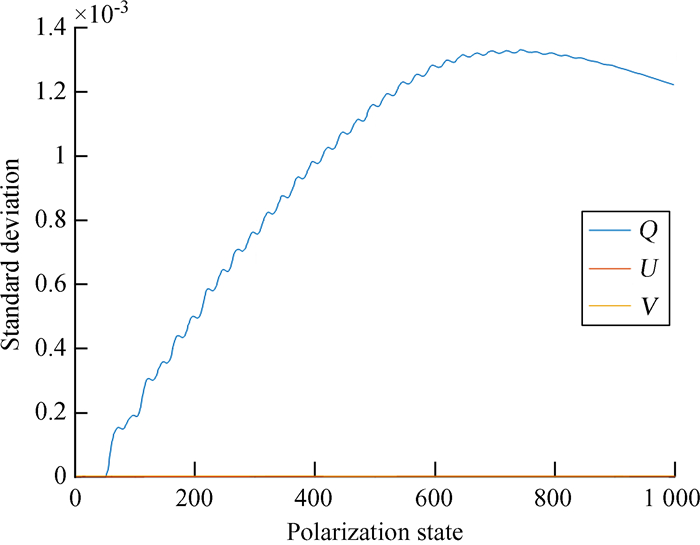
由于DKDP晶体与偏振片在偏振分析器中固定不动,在对DKDP晶体的快轴与偏振片角度完成标定后,其角度误差远小于0.001 rad。我们假定DKDP晶体的快轴与偏振片角度误差均为0.001 rad,验证是否满足测量精度的要求。我们使用相同的方法得到1 000个偏振采样点,并添加一个独立的标准差为0.001的高斯噪声到DKDP2晶体的快轴角度参数,得到受快轴角度误差影响的偏振测量误差。同理得到偏振片角度误差导致的偏振测量误差。
DKDP2快轴角度误差结果见图 9,偏振片角度误差结果见图 10。从图 9和图 10可以看出,在两种角度误差的影响下,测得的斯托克斯矢量中只有Q分量受到DKDP2晶体快轴角度误差和偏振片角度误差的影响,且测量误差小于2 × 10-3,满足偏振测量的要求。由于DKDP晶体固定不动,受到快轴角度误差的影响远远小于传统的波片式结构。
|
| 图 9 DKDP2快轴角度误差结果 Fig. 9 DKDP2 fast axis angle error results |
|
| 图 10 偏振片角度误差结果 Fig. 10 Plarizer angle error results |
最后,我们对两种方案的测量时间进行了对比分析。其中,DKDP晶体毫秒级的响应时间可忽略不计,令相机采集频率为10帧/秒,为了提高精度,每个调制位置采集两帧图像。
表 3和表 4对比可以看出,在单波长点偏振测量中,传统方案测量时间大于16.2 s,是双DKDP方案测量时间(0.8 s) 的20倍以上;在6个波长点的偏振测量中,传统方案测量时间大于111.2 s,双DKDP方案测量时间约为18.8 s。由于波长点切换频率较低,传统方案测量时间为双DKDP方案的6倍左右。因此,采用本文提出的基于双DKDP晶体原理的实时偏振测量方案,在单波长点和多波长点偏振测量中,时间分辨率可分别提高20倍和6倍。
| Modulation frequency | Modulation steps | Camera frequency/(frames/sec) | Image frames/frames | Measuring time/s | |
| Traditional scheme | >5 s | 3 (wave plate) | 10 | 12 | >16.2 |
| Double DKDP scheme | millisecond | 4 | 10 | 8 | ≈0.8 |
| Modulation frequency | Modulation steps | Wavelength point switching time/s | Image frames/frames | Measuring time/s | |
| Traditional scheme | >5 s | 18 | 14 | 72 | >111.2 |
| Double DKDP scheme | millisecond | 24 | 14 | 48 | ≈18.8 |
太阳大气探测在空间天气预报和太阳物理研究等方面发挥着重要作用,而太阳磁场是太阳活动爆发的根本驱动力,偏振测量是实现太阳磁场探测的重要方法。目前偏振测量的主要手段包括旋转波片调制方式与波片+ DKDP晶体调制方式。波片+ DKDP晶体的测量方法相比旋转波片可以减少旋转波片的次数,缩短测量时间,但由于波片结构的存在,仍然需要大量时间,实时性不佳,且容易出现仪器抖动等问题。基于DKDP晶体毫秒级的电光响应速度,本文提出了双DKDP晶体实时偏振测量方法,采用两组DKDP晶体作为偏振调制器件,调制时间可从数秒提高到毫秒级,大大提高了测量的实时性。本文通过仿真验证了方法的可行性,精度优于2 × 10-3,在单波长点和多波长点偏振测量中,时间分辨率是传统方案的20倍和6倍,对太阳大气实时偏振测量有重要意义。
| [1] | YUAN Y, SHIHF Y, JING J, et al. Automated flare forecasting using a statistical learning technique[J]. Research in Astronomy and Astrophysics, 2010, 10(8): 785–796. DOI: 10.1088/1674-4527/10/8/008 |
| [2] | JIANG J, CHATTERJEE P, CHOUDHURIA R. Solar activity forecast with a dynamo model[J]. Monthly Notices of the Royal Astronomical Society, 2007, 381(4): 1527–1542. DOI: 10.1111/j.1365-2966.2007.12267.x |
| [3] | BALTHASAR H, VONDER LVHE O, KNEER F, et al. GREGOR: the new German solar telescope[C]//ASP Conference Series. 2007. |
| [4] | CAO W, GORCEIX N, COULTER R, et al. Scientific instrumentation for the 1.6 m New Solar Telescope in Big Bear[J]. Astronomische Nachrichten, 2010, 331(6): 636–639. DOI: 10.1002/asna.201011390 |
| [5] | WANG R, XU Z, JIN Z Y, et al. The first observation and data reduction of the Multi-wavelength Spectrometer on the New Vacuum Solar Telescope[J]. Research in Astronomy and Astrophysics, 2013, 13(10): 1240–1254. DOI: 10.1088/1674-4527/13/10/012 |
| [6] |
覃瑛, 彭建国, 张涛. NVST偏振观测系统的运动控制实现[J]. 天文研究与技术, 2018, 15(3): 315–322 QIN Y, PENG J G, ZHANG T, et al. The movement and control realization of NVST polarization observation system[J]. Astronomical Research & Technology, 2018, 15(3): 315–322. |
| [7] |
艾国祥, 胡岳风. 太阳磁场望远镜中KD*P电光调制器[J]. 天体物理学报, 1981, 1(4): 273–284 AI G X, HU Y F. The KD*P modulator in the solar magnetic field telescope[J]. Acta Astrophysica Sinica, 1981, 1(4): 273–284. |
| [8] | ANDRIYEVSKY B, PATRYN A, COBET C, et al. Electronic properties of KDP and DKDP crystals: Ab-Initio calculations and spectral ellipsometry experiment[J]. Ferroelectrics, 2011, 417(1): 20–24. DOI: 10.1080/00150193.2011.578461 |
| [9] | PEINADO A, LIZANA A, VIDAL J, et al. Optimization and performance criteria of a Stokes polarimeter based on two variable retarders[J]. Optics Express, 2010, 18(10): 9815–9830. DOI: 10.1364/OE.18.009815 |
| [10] | GU N T, YAO B X, HUANG L H, et al. Design and analysis of a novel compact and simultaneous polarimeter for complete stokes polarization imaging with a piece of encoded birefringent crystal and a micro-polarizer array[J]. IEEE Photonics Journal, 2018, 10(2): 6801312. |



