2. 中国科学院大学, 北京 100049;
3. 中国科学院空间目标与碎片观测重点实验室, 江苏 南京 210034
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Space Object & Debris Observation, Chinese Academy of Sciences, Nanjing 210034, China
激光测距是当前获取目标高精度距离的重要技术手段之一,在监测大陆板块运动、地壳形变、地球自转,改进地球重力场和地心引力参数,确定地球和海洋潮汐的变化规律,监测空间碎片等方面具有重要作用[1-5]。随着商业航天的大力发展,空间目标的数量急剧增长,对空间目标进行有效的高精度测量成为必然。对原始测距数据进行预处理是数据应用的基本前提。
图像的边缘包含图像最基本、最重要的特征,边缘检测的目的是发现图像中关于形状和反射或透射比的信息[6]。目前,卫星激光测距信号的提取方法主要有人工识别和泊松(Poisson) 滤波算法等。本文提出一种基于图像边缘检测的激光测距信号提取方法,结合常规的数据处理方法,提取有效的卫星回波信号。
1 基本原理激光测距是测量激光脉冲往返卫星的飞行时间[7],由于系统噪声、环境噪声等影响,测距残差数据中含有大量的噪声,需要从噪声中识别有效信号。本文处理的对象是测距残差图像,对残差图像进行卷积,得到图像的边缘信息,即信号位置,然后通过图像的对应关系还原到原始信号,这一阶段的数据仍含有噪声,需要对数据进行拟合去噪得到有用信号。
2 方法步骤 2.1 获取测距残差图像本文的原始测距数据来源于云南天文台1.2 m望远镜,观测目标为卫星和部分空间碎片。目前,激光测距系统采用事件计时器作为时间测量设备[3],该器件将每个激光脉冲的发射时刻(主波)与接收时刻(回波) 分别记为A,B事件,将回波与主波进行匹配。匹配过程中,每个B事件(bj)与每个A事件(ai) 的时刻相减,差再减去A事件对应的预报距离时间,当小于等于给定的阈值T时,认为匹配成功[3],即
| $ |({b_j} - {a_i}) - pred({a_i})| \le T, $ | (1) |
遍历(1) 式中的i和j,满足条件时保存主波时刻和匹配成功的回波时刻,然后生成测距残差图像。
2.2 边缘检测图像边缘具有方向和幅度两个特征,沿着图像的边缘方向,像素的灰度变化比较平缓,但在垂直于边缘方向,像素的灰度变化比较剧烈[6]。图像边缘检测的基本原理是用图像一阶导数的局部极大值表示图像的边缘信息。经典的边缘检测方法是对原始图像中所有像素的周围邻域进行卷积运算,这种运算的模块称为检测算子,常用的边缘检测算子有Roberts算子、Sobel算子、Prewitt算子、Kirsch算子、LOG (高斯-拉普拉斯) 算子和Canny算子等。这些方法对处理像素为中心的邻域进行灰度分析,实现图像边缘的提取[8]。
Sobel算子主要利用像素点上下左右邻点的灰度加权算法,具有很好的边缘检测效果,缺点是它同时会检出许多伪边缘。一般来说,对精度要求不高时可以采用这种方法。Sobel算子有两个:(1) 检测水平边缘;(2) 检测垂直边缘。Sobel算子利用快速卷积函数提取图像的边缘,简单高效,因此应用广泛。Sobel算子通常先进行加权平均,然后微分,计算方法为
| $ \begin{array}{*{20}{l}} {{G_x} = \left[ {f\left( {x - 1, y - 1} \right) + 2f\left( {x - 1, y} \right) + f\left( {x - 1, y + 1} \right)} \right] - [f\left( {x + 1, y - 1} \right) + }\\ \ \ \ \ \ \ \ \ \ \ {2f\left( {x + 1, y} \right) + f\left( {x + 1, y + 1} \right)], } \end{array} $ | (2) |
| $ \begin{array}{*{20}{l}} {{G_y} = \left[ {f\left( {x - 1, y + 1} \right) + 2f\left( {x, y + 1} \right) + f\left( {x + 1, y + 1} \right)} \right] - [f\left( {x - 1, y - 1} \right) + }\\ \ \ \ \ \ \ \ \ \ \ {2f\left( {x, y - 1} \right) + f\left( {x + 1, y - 1} \right)], } \end{array} $ | (3) |
其中,Gx和Gy分别代表经横向和纵向边缘检测的图像。(2) 式用于检测水平边缘,(3) 式用于检测垂直边缘。
Sobel算子包含两组3 × 3的矩阵,分别为横向和纵向,与图像作平面卷积可以分别得到横向和纵向的亮度差分近似值。水平变化时,将I与一个奇数内核Gx进行卷积,当内核大小为3时,Gx的计算公式为
| $ {{G_x} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - 1}\\ 2&0&{ - 2}\\ 1&0&{ - 1} \end{array}} \right]*I.} $ | (4) |
垂直变化时,将I与一个奇数内核Gy进行卷积,当内核大小为3时,Gy的计算公式为
| $ {{G_y} = \left[ {\begin{array}{*{20}{c}} 1&2&1\\ 0&0&0\\ {{\rm{ - }}1}&{{\rm{ - }}2}&{{\rm{ - }}1} \end{array}} \right]*I.} $ | (5) |
其中,I为图像G的一部分。循环遍历图像G得到边缘检测后的图像。
以Glonass-129卫星为例,我们对残差图像进行基于Sobel算子的边缘检测。2019年11月15日Glonass-129卫星测距残差原图见图 1。

|
| 图 1 2019年11月15日Glonass-129测距残差原图 Fig. 1 2019-11-15 Glonass-129 original image of ranging residual |
原图转换成灰度图后进行Sobel边缘检测,结果如图 2。这种检测效果不理想,从图 1可以看出,信号集中在中间的蓝色宽线段,经过Sobel边缘检测后,图 1中的边缘信息全部检测并保留下来,同时也检出了一些孤立的噪声点。根据Sobel的数学原理,本文提出了一种针对测距信号的边缘检测方法,设计一个大尺度的卷积核(算子),只进行近似横向的识别,因为在大尺度的残差图中,信号一般近似是一条直线。由于在残差图像信号位置附近,信号密度一般比噪声密度大,经过简单的统计学原则和粗拟合可以去除明显的噪声。

|
| 图 2 2019年11月15日Glonass-129残差图经过Sobel方法边缘检测的结果 Fig. 2 2019-11-15 Glonass-129 residual image after sobel method edge detection |
Sobel算子的大小为3 × 3,9个元素对图像进行遍历卷积。我们分析图 2发现,对于激光测距残差图,小尺寸的卷积操作会保留更多的噪声。因此,本文设计了尺寸为5 × 65的算子
| $ {{O_{\rm{N}}} = \left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1&1\\ 0&0& \cdots &0&0\\ 0&0& \cdots &0&0\\ 0&0& \cdots &0&0\\ { - 1}&{ - 1}& \cdots &{ - 1}&{ - 1} \end{array}} \right]/65} $ | (6) |
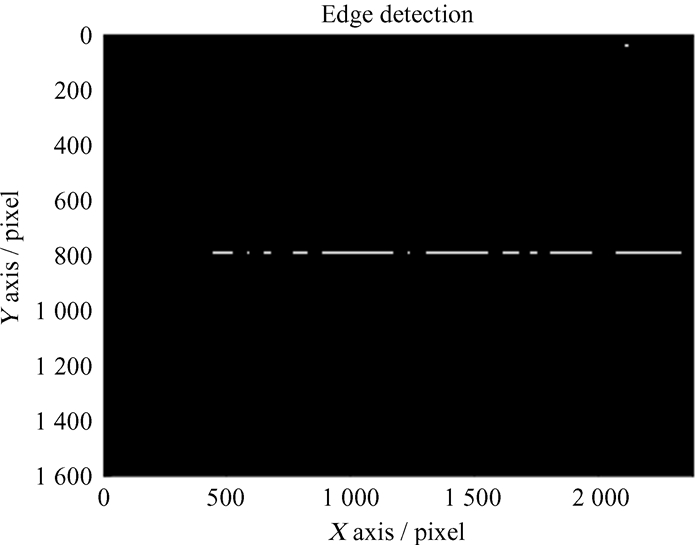
对测距残差图像进行卷积操作,经过新算子处理后的结果如图 3。根据信号长度的特点,我们对一些图像处理后,设置算子经验长度为65,结构类似Sobel算子,第1行与第3行是相反数,第2行设置为0,与Sobel不同的是新算子第1行全部设置为1。在图像转化成灰度图后,为提高计算速度,我们将图像二值化,横向的像素点强度服从均匀分布,同时对矩阵进行零均值和归一化处理。(6) 式中的矩阵是5 × 65,测距残差图像原始尺寸为1 610 × 2 425 × 3 (宽×长×通道),边缘检测结果的图像大小为1 068 × 2 361 (宽×长)。由于对原始图像进行了灰度处理,所以结果变为单通道。
|
| 图 3 2019年11月15日Glonass-129残差图经过超大尺度算子边缘检测的结果 Fig. 3 2019-11-15 Glonass-129 residual image after super-large-scale operator edge detection results |
经过边缘检测,我们最终得到信号在图像中的位置,主波和回波已经在第1步匹配完成,所以此时得到时间信号即可。本文按照图像大小比例和信号位置比例还原时间信号,设原始残差图像为G0,得到的图像为G1,确定G0和G1大小比例系数k,G图起始主波时刻A0,G1中每个信号点的横坐标Ci对应的原始主波时刻计算公式为
| $ {C_i} = {A_{{\rm{min}}}}{\rm{|}}({A_0} + {B_i}k){\rm{|}}. $ | (7) |
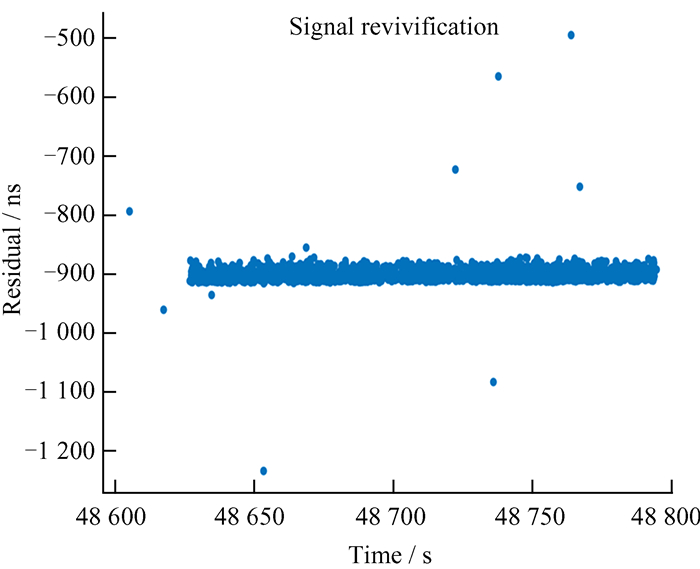
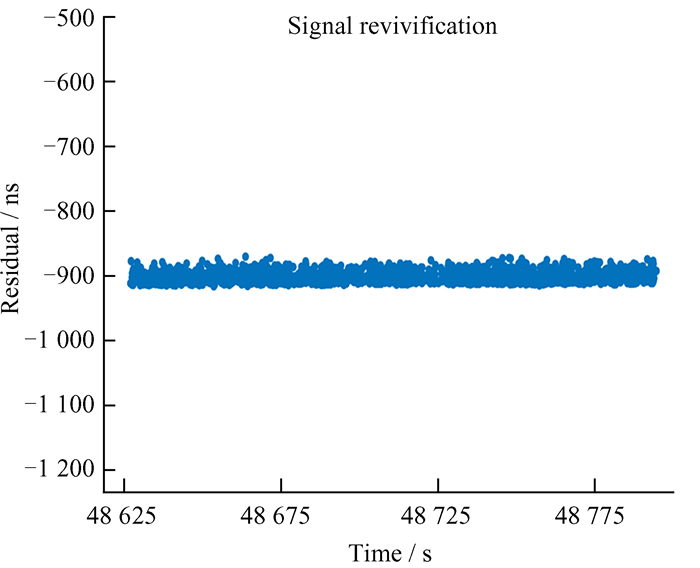
其中,Bi是图G1中的信号横坐标值(像素);Amin是A0+Bik的值在主波A中最接近的一个值。此时得到的信号为粗略信号,意味着还原的主波数据中还包含部分噪声,如图 4。经过粗略去除噪声的结果如图 5。
|
| 图 4 2019年11月15日Glonass-129数据还原后含有噪声的图像 Fig. 4 2019-11-15 Glonass-129 data contains noisy results after restoration |
|
| 图 5 Glonass-129数据还原后粗略去除噪声的结果 Fig. 5 Glonass-129 data reduction results after rough reduction |
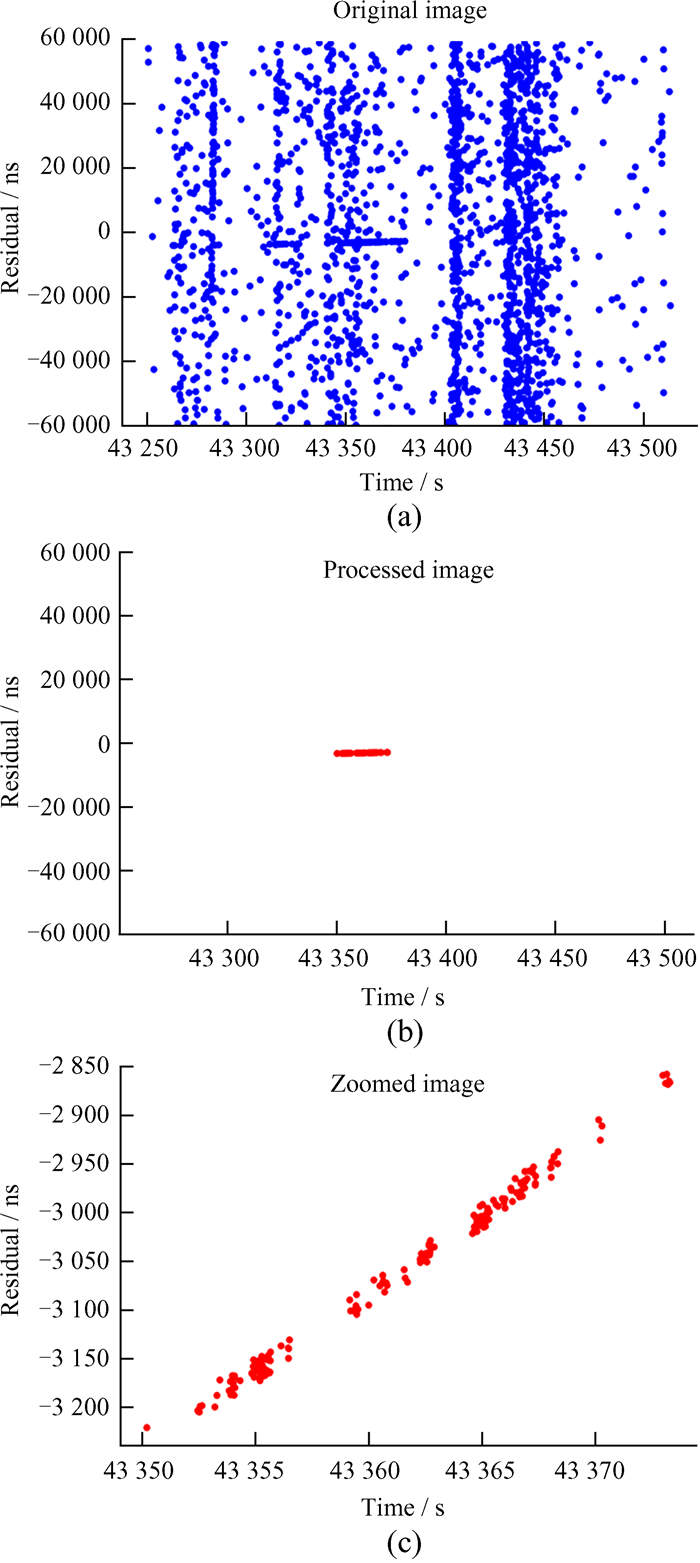
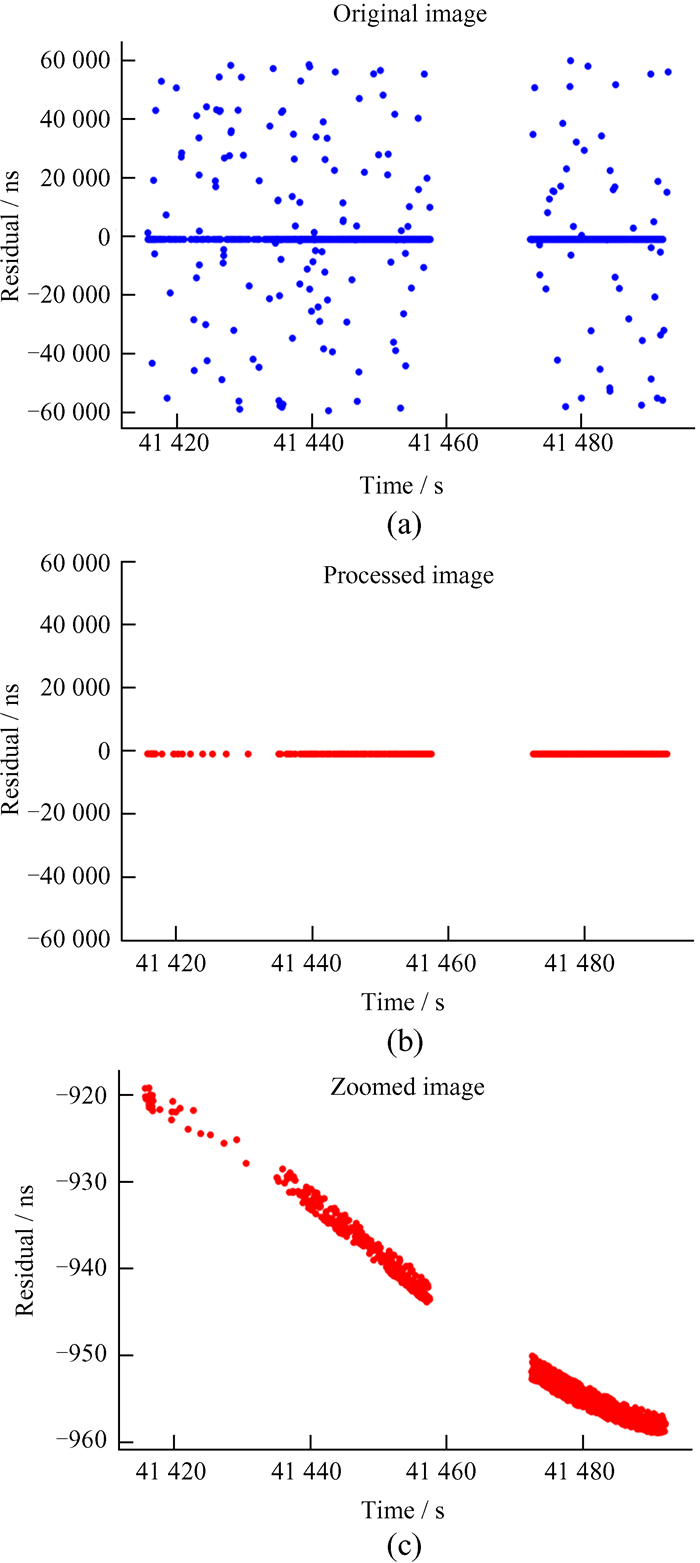
本文仅对一些典型卫星和空间碎片的原始信号进行边缘检测,结果如图 6~图 9。目标边缘检测的精度分析见表 1,第1列NORAD ID是北美防空司令部空间物体的编号;第2列是雷达散射截面积(Radar Cross Section, RCS);第3列是双向测距精度(激光器脉宽7 ns),子列Edge_M是边缘检测方法的精度,Graz是测距数据处理方法的精度;第4列是两种方法识别信号点的数量。
|
| 图 6 (a) 37731空间碎片的原始图像;(b) 边缘检测后的信号残差图;(c) 放大显示的残差图 Fig. 6 (a) Original image of 37731 space debris; (b) signal residual image after edge detection; (c) enlarged residual image |
|
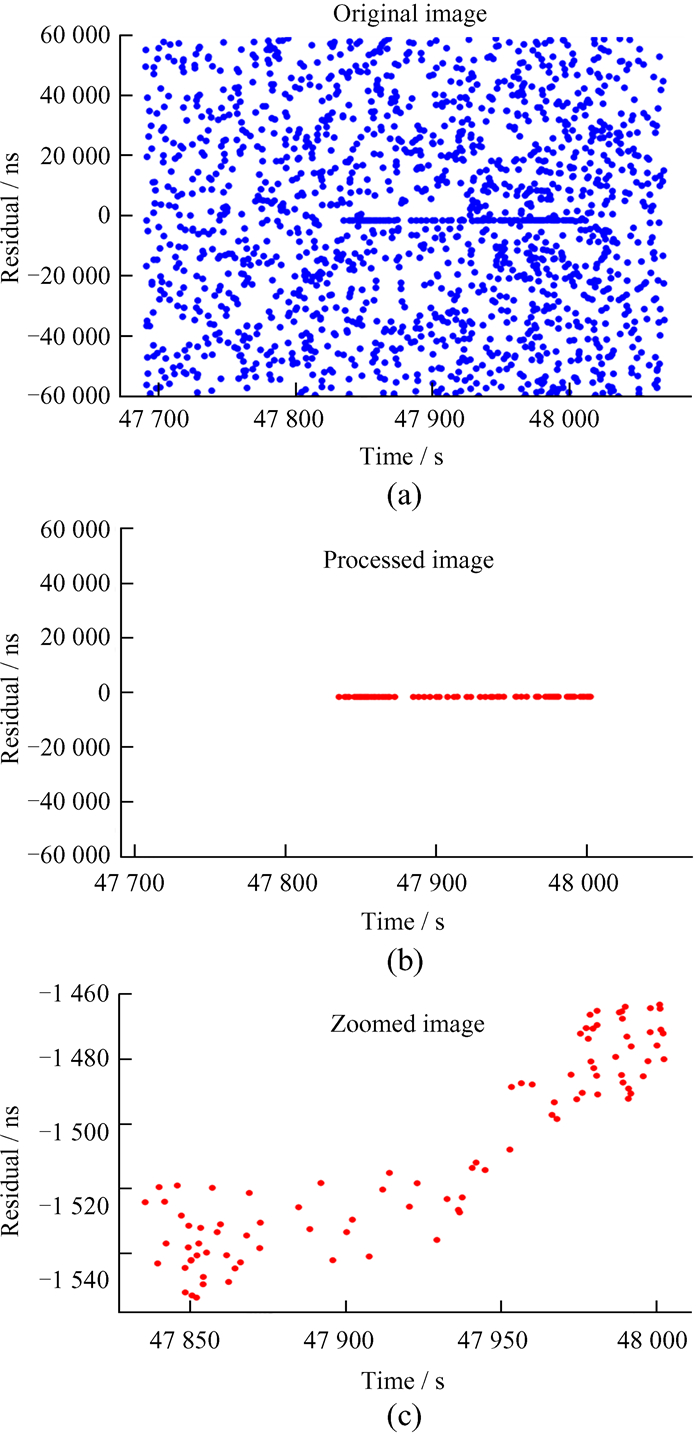
| 图 7 (a) Beaconc卫星的原始图像;(b) 边缘检测后的信号残差图;(c) 放大显示的残差图 Fig. 7 (a) Original image of Beaconc satellite; (b) signal residual image after edge detection; (c) enlarged residual image |
|
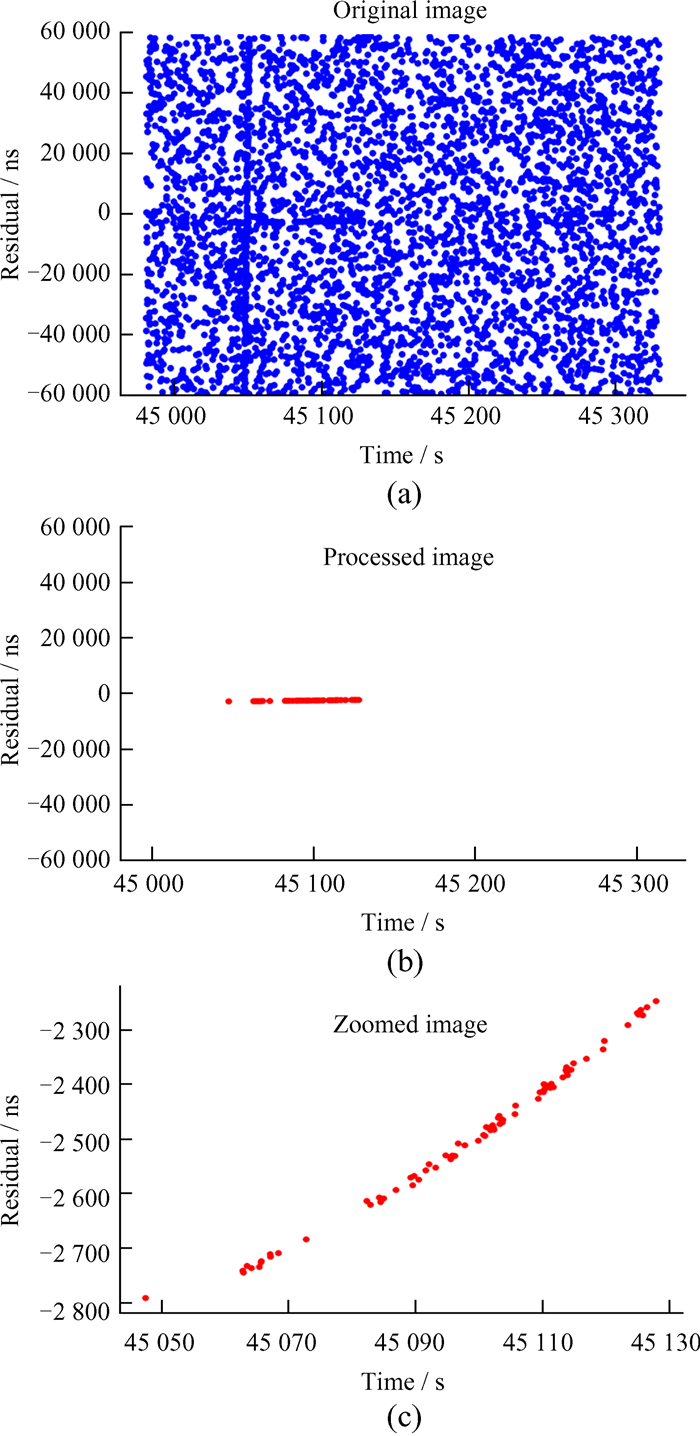
| 图 8 (a) 021108空间碎片的原始图像;(b) 边缘检测后的信号残差图;(c) 放大显示的残差图 Fig. 8 (a) Original image of 021108 space debris; (b) signal residual image after edge detection; (c) enlarged residual image |
|
| 图 9 (a) 09904空间碎片的原始图像;(b) 边缘检测后的信号残差图;(c) 放大显示的残差图 Fig. 9 (a) Original image of 09904 space debris; (b) signal residual image after edge detection; (c) enlarged residual image |
| NORAD ID | RCS/m2 | Precision/cm | Number | |||
| Edge_M | Graz | Edge_M | Graz | |||
| 37731 | 8.527 0 | 213.1 | 256.3 | 164 | 131 | |
| 021108 | 5.669 6 | 285.2 | 330.9 | 94 | 52 | |
| 09904 | 7.716 1 | 174.5 | 175.6 | 79 | 46 | |
| 1328 (Beaconc) | 2.265 1 | 40.4 | 39.7 | 1 454 | 1 417 | |
| 17908 (Ajisai) | 3.981 1 | 80.4 | 82.0 | 34 021 | 35 364 | |
通过3.1的结果可以看出,边缘检测方法识别的信号长度较原图短,即初始识别存在漏点,主要原因是卷积核矩阵的长度过长。为了保持数据量不变,我们采取一种简单的扩充方式,把边缘检测每段结果的长度左右扩大,只要残差符合给定阈值即认为是信号,后期再进行拟合分析。从表 1可以看出,碎片的精度大致在米级,Beaconc和Ajisai卫星的精度为分米级。
通过以上分析可知,信号数量较少时,检测效果不理想,需要手动调整卷积核的大小。另外,新的卷积核计算比较耗时,这是接下来改进的方向。
4 结论本文提出了一种基于图像边缘检测识别激光测距信号的方法,该方法处理的对象是测距残差图像,对其进行图像边缘检测,利用新的大尺度卷积核完成特定目标检测,最后根据数学关系还原主波和回波信号。为了特殊目标的需求,本文设计了专用的卷积核(算子),对目标的精度分析表明该方法的有效性。
| [1] |
叶叔华, 黄珹. 天文地球动力学[M]. 济南: 山东科学技术出版社, 2000. YE S H, HUANG C. Astrogeodynamics[M]. Jinan: Shandong Science and Technology Publishing House, 2000. |
| [2] |
何芸, 刘祺, 田伟, 等. 地月第二拉格朗日点卫星激光测距技术研究[J]. 深空探测学报, 2017, 4(2): 130–137 HE Y, LIU Q, TIAN W, et al. Study on laser ranging for satellite on the second Lagrange point of Earth-Moon system[J]. Journal of Deep Space Exploration, 2017, 4(2): 130–137. |
| [3] |
门涛, 谌钊, 徐蓉, 等. 空间目标激光测距技术发展现状及趋势[J]. 激光与红外, 2018, 48(12): 1451–1457 MEN T, SHEN Z, XU R, et al. Development status and tendency of space target laser ranging technique[J]. Laser & Infrared, 2018, 48(12): 1451–1457. DOI: 10.3969/j.issn.1001-5078.2018.12.001 |
| [4] |
李熙, 汤儒峰, 李祝莲, 等. 基于二值图像的卫星激光测距数据处理[J]. 中国激光, 2014, 41(12): 182–189 LI X, TANG R U, LI Z L, et al. Laser ranging data processing based on the analysis of the binary image[J]. Chinese Journal of Lasers, 2014, 41(12): 182–189. |
| [5] |
赵春梅, 桑吉章, 翟锋, 等. 空间目标激光测距技术及应用[M]. 北京: 科学出版社, 2015. ZHAO C M, SANG J Z, ZHAI F, et al. Laser ranging technology and application of space target[M]. Beijing: Science Press, 2015. |
| [6] |
段瑞玲, 李庆祥, 李玉和. 图像边缘检测方法研究综述[J]. 光学技术, 2005, 31(3): 415–419 DUAN R L, LI Q X, LI Y H. Summary of image edge detection[J]. Optical Technique, 2005, 31(3): 415–419. DOI: 10.3321/j.issn:1002-1582.2005.03.028 |
| [7] | 汤儒峰. 空间目标激光测距信号处理与应用[D]. 昆明: 中国科学院云南天文台, 2015. TANG R F. Research on characteristics of the spatial target based on laser ranging technology[D]. Kunming: Yunnan Observatories, Chinese Academy of Sciences, 2015. |
| [8] |
孙红艳, 张海英. 图像边缘检测算法的比较与分析[J]. 菏泽学院学报, 2010, 32(2): 49–52 SUN H Y, ZHANG H Y. The comparison and analysis of image edge detection algorithms[J]. Journal of Heze University, 2010, 32(2): 49–52. DOI: 10.3969/j.issn.1673-2103.2010.02.014 |



