2. 中国科学院国家天文台, 北京 100101
2. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China
现代宇宙学中,基于对宇宙微波背景(Cosmic Microwave Background, CMB) 辐射温度图中的小扰动的观测,我们建立了宇宙大尺度结构形成理论。但是对于从宇宙微波背景辐射最后散射面(z~1 100) 到宇宙完全电离(z~6) 这段漫长的宇宙演化历史,很多理论尚未经过观测验证。一般认为,从最后散射面到宇宙中最早的发光天体第1代恒星形成(z~30) 之前,宇宙处于完全透明的黑暗时代(Dark Ages, DA)。第1代恒星产生之后,宇宙黎明(Cosmic Dawn, CD) 开始,期间第1代恒星产生的辐射显著改变了宇宙的辐射背景、气体的电离度和温度等。之后,随着第1代星系的批量形成(z~15),再电离时期(Epoch of Reionization, EoR) 开始。在星系和类星体等发出的电离光子的驱动下,星系际介质(Intergalactic Medium, IGM) 快速电离和加热,一直到z~6左右,几乎所有的星系际介质再次回到电离状态,宇宙中残余的中性氢(Neutral Hydrogen, HI) 主要在星系内部,再电离时期结束。
对于黑暗时代、宇宙黎明和再电离时期的观测是低频射电天文研究的重要内容。在过去20年里,地基低频射电天文学的研究主要在30 MHz以上,在该频率以下,无线电波受到电离层影响而严重畸变,在10 MHz以下则几乎完全被反射。因而,对于理论上位于30 MHz以下的黑暗时代吸收谷的观测,只能通过空间射电望远镜进行。月球的背面为射电天文观测提供了一个独特的射电静谧区,它不受地面射频干扰,且电离层非常薄。作为空间低频射电天文的探路者,搭载于嫦娥四号着陆器的低频射电频谱仪已于2019年1月3日成功着陆,并观测获得了首批数据。本文评估2C级数据对黑暗时代信号的探测能力。
1 21 cm整体谱中性氢原子存在电子自旋和核自旋平行(0能级)与反平行(1能级) 的超精细能级结构,能级跃迁会吸收或辐射21 cm波长谱线。我们定义T*≡hc/kBλ21 cm=0.068 K,两个能级氢原子的数密度比可以由中性氢的自旋温度TS描述,
| $ {n_1}/{n_0} = ({g_1}/{g_0}){\text{exp}}( - {T_*}/{T_{\text{S}}}), $ | (1) |
统计简并度比g1/g0=3。根据辐射转移理论可以得到21 cm线微分亮温度
| $\begin{array}{*{20}{l}} \delta {T_{\text{b}}} = \frac{{{T_{\text{S}}} - {T_{\text{R}}}}}{{1 + z}}(1 - {{\text{e}}^{ - {\tau _\nu }}}) \hfill \\ \begin{array}{*{20}{l}} {\;\;\;\;\; \approx \frac{{{T_{\text{S}}} - {T_{\text{R}}}}}{{1 + z}}\tau } \\ {\;\;\;\;\; \approx 21{x_{{\text{HI}}}}\left( {1 + {\delta _{\text{b}}}} \right)\left( {\frac{{{\mathit{\Omega }_{\text{b}}}{h^2}}}{{0.023}}} \right){{\left( {\frac{{0.15}}{{{\mathit{\Omega }_{\text{m}}}{h^2}}}\frac{{1 + z}}{{10}}} \right)}^{1/2}}\left( {\frac{{{T_{\text{S}}} - {T_{\text{R}}}}}{{{T_{\text{S}}}}}} \right)\left[ {\frac{{{\partial _{\text{r}}}{v_{\text{r}}}}}{{\left( {1 + z} \right)H\left( z \right)}}} \right]{\text{mK}}, } \\ \end{array} \hfill \\ \end{array} $ | (2) |
其中,TR为背景辐射温度;τν为谱线光深;z为宇宙学红移;xHI为中性氢电离度;δb为重子密度涨落比分数;Ωb和Ωm分别为重子物质与暗物质的密度参量;H(z) 为哈勃参量,约化哈勃参量
自旋温度主要由3个物理过程共同决定:(1)从(向)背景辐射吸收(辐射) 21 cm光子;(2) 与其他中性原子及电子的碰撞;(3) 莱曼α光子的共振散射导致通过中间激发态的自旋翻转。这些过程远快于退激发时间,所以通过平衡态方程可以近似给出自旋温度
| $ T_{\text{S}}^{ - 1} = \frac{{T_\gamma ^{ - 1} + {x_{\text{α }}}T_{\text{α }}^{ - 1} + {x_{\text{c}}}T_{\text{K}}^{ - 1}}}{{1 + {x_{\text{α }}} + {x_{\text{c}}}}}, $ | (3) |
其中,Tγ为光子的环境温度,近似地Tγ=TCMB;Tα为莱曼α辐射场色温度;TK为气体动力学温度;xα与xc为相应过程的耦合系数。当总耦合系数
从观测角度,背景辐射源主要有两类:宇宙微波背景辐射或射电噪点源,后者对应于“21 cm森林”的观测,本文主要讨论前者。当TR=TCMB时,21 cm信号表现为宇宙微波背景辐射黑体谱在射电波段的微小扰动。对21 cm信号的观测分为两类:(1) 考虑空间扰动的功率谱测量或成像测量;(2) 对全天所有方向平均的整体谱测量,即测量
| $ \overline {\delta {T_{\text{b}}}} \left( \nu \right) = \smallint {\text{d}}\mathit{\Omega }\delta {T_{\text{b}}}(\hat r, \nu ). $ | (4) |
功率谱测量需要望远镜有足够高的空间分辨率,通常由射电阵列观测。通过嫦娥四号中继通信卫星上搭载的中荷低频射电探测仪(The Netherland-China Low Frequency Explorer, NCLE) 与低频射电频谱仪进行空间低频射电干涉测量[2],有望探测到21 cm信号的功率谱。整体谱的观测可通过单天线实现,本文评估低频射电频谱仪的2C级数据对于宇宙黑暗时代21 cm信号整体谱的探测能力。
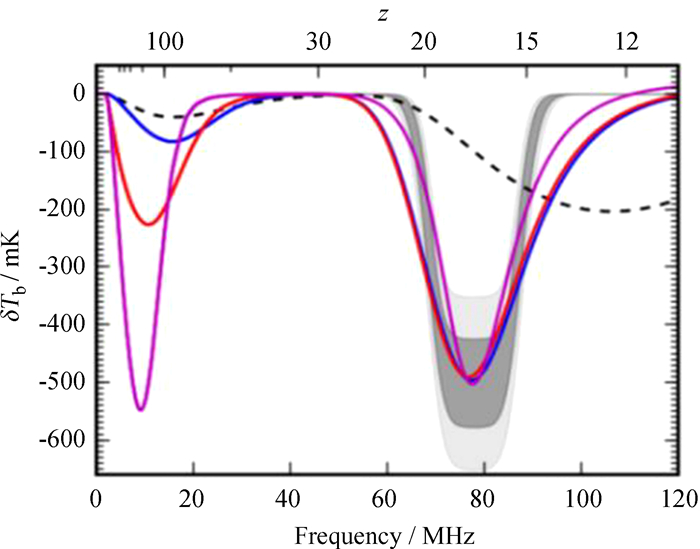
21 cm信号蕴含丰富的信息,它由宇宙学参数与天体物理学参数共同决定。考虑到星系际介质密度、电离状态和热状态的演化以及天体的形成,不同阶段的21 cm整体谱信号表现出不同的特征,不同模型(参数) 的信号差异也较大,其理论值可由纯流体动力学模拟[3]、半解析模拟[4]或基于神经网络的仿真器[5]给出。图 1给出不同模型下的21 cm整体谱示例(详见文[6]),横坐标分别为中性氢谱线的观测频率及对应的宇宙学红移,纵坐标为21 cm线微分亮温度。图中的黑色虚线对应标准宇宙学模型;灰色区域是重子物质与暗物质相互作用的参数化模型;阴影区域分别是与“边缘”实验(Experiment to Detect the Global Epoch of reionization Signature, EDGES) 观测结果[7]一致的1σ和2σ置信区间;蓝色曲线假设早于标准模型的绝热冷却;红色曲线冷却更早且冷却率更低;紫色曲线假设冷却速率非单调下降,而是存在一个过冷却时期。现有模型普遍认为z > 30存在黑暗时代吸收谷,30 > z > 15存在宇宙黎明吸收谷,15 > z > 6存在再电离时期发射线,信号大小为10~102 mK量级。
2 前景辐射21 cm信号观测充满挑战,主要在于将微弱信号从高数个量级的前景辐射中分离。在低频射电波段,银河系的同步辐射占主导,一个合理的亮温度模型近似为
| $ {T_{{\rm{syn}}}}\left( \nu \right) = {A_{{\rm{syn}}}}{\left( {\frac{\nu }{{{\nu _0}}}} \right)^{ - {\alpha _{{\rm{syn}}}} - \Delta {\alpha _{{\rm{syn}}}}{\rm{ln}}\left( {\nu /{\nu _0}} \right)}}, $ | (5) |
其中,ν为观测频率;谱指数αsyn≈2.8;谱指数跑动Δαsyn≈0.1;ν0为(任意的) 中心频率,与特定频率的总体振幅简并[8]。当ν0=150 MHz时,Asyn=335.4 K。对于银河系的自由-自由辐射(在150 MHz处约占总体前景辐射的1%),我们同样采用跑动幂率谱近似,
| $ {T_{{\rm{ff}}}}\left( \nu \right) = {A_{{\rm{ff}}}}{\left( {\frac{\nu }{{{\nu _0}}}} \right)^{ - {\alpha _{{\rm{ff}}}} - \Delta {\alpha _{{\rm{ff}}}}{\rm{ln}}\left( {\nu /{\nu _0}} \right)}}, $ | (6) |
其中,αff≈2.15;Δαff≈0.01;Aff=33.5 K。此外,明亮射电源、未知点源以及尘埃辐射等组成的前景污染同样不容忽视。
然而,由于星系际介质在视线上的密度、电离状态和温度的不均匀性,21 cm信号在光谱上是高度变化的,而非热前景辐射光谱则是平滑的,这为分离前景辐射与信号提供了便利,但前提是需要消除任何仪器效应造成前景扰动带来的污染[9]。
3 2C数据频谱2019年1月3日,嫦娥四号着陆器成功着陆月球背面南极-艾特肯盆地冯-卡门撞击坑。嫦娥四号着陆器搭载的低频射电频谱仪安装在着陆器顶板,包括4根接收天线、前置放大器和电子学单元。4根接收天线中,A,B和C天线互相正交且长度均为5 m,D天线为长度20 cm的短天线。低频射电频谱仪的工作频率为100 kHz~2 MHz和1~40 MHz两个频段,频率分辨率为5 kHz和100 kHz。在低频射电频谱仪的数据处理过程中,首先对4根天线的原始电压观测量进行快速傅里叶变换,根据一定时间间隔内每根长天线与天线D频谱幅值间的比值确定对消系数,再以长天线频谱幅值减去天线D的频谱幅值乘以对消系数,得到2C观测数据[10]。
在低频射电波段,辐射亮温度定义为
| $ {T_{\rm{b}}} = \frac{{{I_\nu }}}{{2k}}\frac{{{c^2}}}{{{\nu ^2}}}, $ | (7) |
其中,k为玻尔兹曼常数;c为光速;ν为谱线频率;辐射强度Iν由单位立体角的流量密度决定,即
| $ {I_\nu } = \frac{{{S_\nu }}}{{{\rm{d}}\mathit{\Omega }}}. $ | (8) |
根据有效面积的定义[11],我们可由谱功率Pν得到总流量密度为
| $ {S_\nu } = \frac{{2{P_\nu }}}{{\langle {A_{{\rm{eff}}}}\rangle }}, $ | (9) |
其中,Pν由每个频率通道的接收功率除以谱频分辨率得到。对于所有的无损失天线,平均有效接收面积正比于波长λ2[11],即
| $ \left\langle {{A_{e{\rm{ff}}}}} \right\rangle = \frac{{{\lambda ^2}}}{{4{\rm{ \mathsf{ π} }}}}. $ | (10) |
通常低频单机子天线在高频(High Frequency, HF) 频带的天线效率η取值的动态范围10%~80%,我们将2C数据基线功率频谱转化为亮温度频谱,即
| $ {\overline T _{\rm{b}}} = \frac{{4{\rm{ \mathsf{ π} }}{P_\nu }}}{{\eta k}}. $ | (11) |
基于上述过程,我们对2019年1月~4月的2C级别数据做了长时间积分,并分别给出A,B和C天线测量的亮温度频谱上下限。结果如图 2中阴影区域,横纵坐标分别表示观测频率和亮温度。假设天线效率10%~80%,图 2给出A,B和C天线测量的亮温度上下限(阴影区域),蓝色和橙色曲线为银河系同步辐射和自由-自由辐射的理论值(分别由(5)式和(6)式计算得出)。图 2同时给出银河系前景辐射的理论曲线用于比较,结果显示,2C数据基线频谱低于前景辐射4~5个数量级。

|
| 图 2 低频射电频谱仪2C数据(2019年1~4月) 基线频谱 Fig. 2 The baseline spectrum of the Low Frequency Radio Spectrometer 2C data (Jan.-Apr. 2019) |
上述结果表明,2C数据基线频谱低于银河系前景辐射4~5个数量级,因而几乎不包含前景辐射信号,也无法使用前景辐射的仿真数据对2C数据进行定标校准。因此,我们需要更低级别的数据,从中寻找造成该结果的原因,并对更低级别的数据进行多种数据处理方法的对比研究,以便进一步评估嫦娥四号低频射电频谱仪对宇宙黑暗时代的探测能力。
致谢: 我们感谢张志嵩在数据分析部分的深度讨论和建议,感谢陈林杰和张墨关于文稿的修改建议,也感谢所有参与本项目并做出贡献的同事们。
| [1] | PRITCHARD J R, LOEB A. 21 cm cosmology in the 21st century[J]. Reports on Progress in Physics, 2012, 75(8): 086901. DOI: 10.1088/0034-4885/75/8/086901 |
| [2] |
武宇翔, 温卫斌, 平劲松, 等. 利用Halo轨道仿真开展嫦娥四号中继星与月面设备干涉基线的研究[J]. 天文研究与技术, 2021, 18(1): 69–76 WU Y X, WEN W B, PING J S, et al. Research of interferometry baselines between CE-4 rover and lunar facility using Halo orbit simulation[J]. Astronomical Research & Technology, 2021, 18(1): 69–76. |
| [3] | TRAC H, CEN R, LOEB A. Imprint of inhomogeneous hydrogen reionization on the temperature distribution of the intergalactic medium[J]. The Astrophysical Journal, 2008, 689(2): L81. DOI: 10.1086/595678 |
| [4] | MESINGER A, FURLANETTO S, CEN R. 21CMFAST: a fast, seminumerical simulation of the high-redshift 21-cm signal[J]. Monthly Notices of the Royal Astronomical Society, 2011, 411(2): 955–972. DOI: 10.1111/j.1365-2966.2010.17731.x |
| [5] | COHEN A, FIALKOV A, BARKANA R, et al. Emulating the global 21-cm signal from Cosmic Dawn and reionization[J]. Monthly Notices of the Royal Astronomical Society, 2020, 495(4): 4845–4859. DOI: 10.1093/mnras/staa1530 |
| [6] | BURNS J O, HALLINAN G, LUX J, et al. FARSIDE: a low radio frequency interferometric array on the lunar farside[J]. Bulletin of the AAS, 2019, 51(7): 1–13. |
| [7] | BOWMAN J D, ROGERS A E E, MONSALVE R A, et al. An absorption profile centred at 78 megahertz in the sky-averaged spectrum[J]. Nature, 2018, 555(7694): 67–70. DOI: 10.1038/nature25792 |
| [8] | WANG X M, TEGMARK M, SANTOS M G, et al. 21 cm tomography with foregrounds[J]. The Astrophysical Journal, 2006, 650: 529–537. DOI: 10.1086/506597 |
| [9] | KERN N S, DILLON J S, PARSONS A R, et al. Absolute calibration strategies for the Hydrogen Epoch of Reionization Array and their impact on the 21 cm power spectrum[J]. The Astrophysical Journal, 2020, 890(2): 122. DOI: 10.3847/1538-4357/ab67bc |
| [10] |
张韬, 苏彦. 嫦娥四号低频射电频谱仪降低背景噪声方法的研究[J]. 天文研究与技术, 2019, 16(3): 312–320 ZHANG T, SU Y. Research of the method for reducing background of very low frequency radio spectrumon Chang'E-4[J]. Astronomical Research & Technology, 2019, 16(3): 312–320. |
| [11] | CONDON J J, RANSOM S M. Essential radioastronomy[M]. Princeton: Princeton University Press, 2016: 75-76. |