2. 南京大学天文与空间科学学院, 江苏 南京 210093
2. School of Astronomy and Space Science, Nanjing University, Nanjing 210093, China
众所周知,耀变体的一个显著特征是电磁辐射具有大幅度和快速的光变,光变出现在整个电磁波频谱范围内的各个波段,而且还具有由短到长各种不同的时标[1]。了解光变的物理过程能帮助我们更好地理解喷流中辐射区的结构、物理条件的演化以及粒子的加速机制和辐射区位置等重要问题。
目前,引起光变的原因尚不清楚,主要有几种可能的解释[2]:内激波机制、湍流-磁重联机制、几何效应机制和外部因素机制。在内激波机制中,喷流的非均匀性导致了相对论性激波的产生,喷流中传播的激波在波前区将粒子加速,从而产生光变[3-6]。另外,喷流有可能产生湍流,进而可能诱发磁重联[7-11]。磁重联可以产生硬的相对论性电子能谱[12]。还有一种可能的机制是光变的几何效应起源[13-16]。由于在喷流的甚长基线干涉测量技术(Very Long Baseline Interferometry, VLBI) 观测中经常看到弯曲或者螺线型的结构,所以这种机制是把光变的主要因素解释为弯曲或者螺线型的喷流路径。因为路径上不同位置的辐射区具有不同的多普勒因子,从而主导了光变。最后一种喷流或者喷流中的高能辐射区通过和外部物质进行直接碰撞或者辐射相互作用而产生光变[17-19]。由于本文主要研究喷流内在的光变物理特性,所以最后这种机制不在本文的考虑范围内。
光变的研究内容包括光变曲线以及从中提取的光变时标,各波段能谱形状在光变过程中的变化,各波段光变曲线之间的相关性、延迟性,光变的周期性、功率谱分析等性质[20-21],还有对光变过程中某个时刻得到的同时/准同时性光谱能量分布的研究[22]。对光谱能量分布的研究由于能通过模型拟合把观测到的光谱能量分布随时间变化的性质和喷流内部物理条件的变化联系起来,为光变过程提供较多的物理信息。以下我们把一个同时/准同时性光谱能量分布数据描述的状态简称为一个“态”,一次光变过程一般包含若干个态。
自1991年EGRET (the Energetic Gamma-Ray Experiment Telescope) 首次探测到λ射线波段以来[23],3C 279成为被观测最频繁的耀变体之一[23-28]。它属于耀变体的一个子类(平谱射电类星体),具有典型的耀变体特征。3C 279有一个明显的射电喷流,在整个电磁波谱中都存在光变。最近,文[28]分析了视界望远镜在20微角秒分辨率下对3C 279内喷流的观测数据,得到3C 279辐射区结构和光变的精细化信息。但是在γ射线波段的分辨率依然不足以直接分辨精细结构,所以关于高能辐射的信息,如辐射区位置等只能用间接推断的方式得到[29]。
由于具有丰富的观测数据,3C 279的光变曾多次作为研究对象[30-34]。截至目前,3C 279的光变研究一般只集中于一次或者数次耀发的个案,或者对某个时段内的数个耀发,而且不同的作者使用的模型不同。如文[30]-32]使用双拐折幂律谱电子能谱分布的单区轻子模型分别对2008年8月~2010年8月的8个态和2013年12月~2014年4月的4个态进行了拟合;文[35]使用拐折幂律谱电子能谱分布的单区轻子模型对2014年3月~4月的γ射线波段的耀发事件进行了拟合;文[36]使用拐折幂律谱电子能谱分布的含时轻子强子模型和双区轻子模型对2013年12月的硬γ射线波段的耀发事件进行了拟合;文[37]使用对数抛物谱电子能谱分布的单区轻子模型和单区轻子强子模型对2015年6月的耀发事件进行了拟合;文[38]使用拐折幂律谱电子能谱分布的单区模型对2018年1月的耀发事件进行了拟合;文[39]使用拐折幂律谱电子能谱分布的单区轻子模型对2015年6月中旬的耀发事件进行了拟合;文[33]使用含时单区均匀模型研究了3C 279的16个态,是迄今为止态数量最多的研究。但是这些研究中态的样本数量依然不足以支持有统计意义的分析结果。所以本文搜集了一个含有3C 279共29个态的样本,对该源光变时外在观测和内在物理特性进行统计研究。
1 同时/准同时性光谱能量分布数据样本本文从[30, 32, 35-39]中搜集了3C 279的29个态的光谱能量分布数据作为样本,观测的光谱能量分布数据是从射电波段到γ射线波段。文[40]-41]指出,射电波段数据的流量产生于外喷流,在
| Time period (MJD) (1) |
R /(1017cm) (2) |
B/G (3) |
δ (4) |
r/pc (5) |
N (6) |
γmin (7) |
γmax (8) |
γb (9) |
p1 (10) |
p2 (11) |
χ2 (d.o.f) (12) |
| 54682~55728 | 0.68 | 0.275 | 17.0 | 0.80 | 1.90 | 60 | 6.00 × 104 | 7.50 × 102 | 2.00 | 3.75 | 15.48/20 |
| 54789~54809 | 0.87 | 0.300 | 20.0 | 0.58 | 1.70 | 60 | 4.00 × 104 | 1.50 × 103 | 2.40 | 3.98 | 4.09/9 |
| 54827~54877 | 0.39 | 0.455 | 20.0 | 0.44 | 6.00 | 60 | 1.00 × 106 | 1.80 × 103 | 2.40 | 4.30 | 6.47/17 |
| 54880~54885 | 1.08 | 0.280 | 20.0 | 0.68 | 0.76 | 60 | 1.00 × 106 | 1.61 × 103 | 2.20 | 4.55 | 5.36/10 |
| 54897~54900 | 0.18 | 0.500 | 27.0 | 0.85 | 1.00 | 240 | 5.00 × 104 | 1.13 × 103 | 2.70 | 4.55 | 6.33/10 |
| 54950~54960 | 2.20 | 0.250 | 14.0 | 1.40 | 0.50 | 60 | 1.00 × 106 | 1.35 × 103 | 2.20 | 4.65 | 1.19/7 |
| 55042~55045 | 0.61 | 0.240 | 20.0 | 0.92 | 0.55 | 150 | 1.00 × 105 | 1.80 × 103 | 2.30 | 4.10 | 2.87/7 |
| 55240~55319 | 0.26 | 0.350 | 25.0 | 1.17 | 3.80 | 100 | 1.00 × 106 | 6.00 × 103 | 2.30 | 4.40 | 9.01/7 |
| 56642~56645 | 1.25 | 0.315 | 16.5 | 0.91 | 0.50 | 80 | 1.00 × 106 | 1.20 × 103 | 2.20 | 4.45 | 4.87/19 |
| 56646.4~56646.6 | 0.55 | 0.260 | 17.0 | 0.11 | 0.47 | 60 | 1.00 × 106 | 2.10 × 103 | 1.70 | 3.80 | 3.26/5 |
| 56657~56660 | 1.50 | 0.230 | 17.0 | 0.95 | 0.11 | 150 | 1.00 × 105 | 1.10 × 103 | 1.90 | 4.10 | 4.49/22 |
| 56750.210~56750.477 | 1.90 | 0.171 | 21.0 | 0.63 | 0.02 | 350 | 5.00 × 104 | 8.50 × 102 | 1.95 | 3.90 | 8.22/15 |
| 57174~57186 | 0.76 | 0.375 | 19.0 | 0.73 | 0.40 | 60 | 1.00 × 106 | 1.50 × 103 | 1.98 | 4.20 | 3.14/6 |
| 57189 | 0.97 | 0.103 | 22.0 | 0.90 | 1.30 | 60 | 1.00 × 106 | 2.70 × 103 | 1.90 | 4.40 | 1.56/11 |
| 57191~57203 | 0.63 | 0.295 | 19.0 | 0.68 | 0.64 | 80 | 1.00 × 106 | 1.90 × 103 | 1.89 | 4.50 | 2.17/9 |
| 58134~58138 | 0.25 | 0.221 | 38.4 | 1.00 | 0.70 | 200 | 3.00 × 106 | 1.30 × 103 | 2.00 | 3.90 | 2.43/16 |
| 58138~58142 | 0.34 | 0.261 | 38.4 | 1.40 | 1.50 | 60 | 1.20 × 106 | 7.00 × 102 | 1.70 | 3.50 | 4.49/15 |
| 58150.2~58151.2 | 0.35 | 0.215 | 38.4 | 0.99 | 0.71 | 80 | 2.50 × 104 | 1.00 × 103 | 1.80 | 3.85 | 9.89/12 |
| 57184~57187 | 1.05 | 0.190 | 16.0 | 1.15 | 0.50 | 100 | 1.00 × 106 | 1.50 × 103 | 1.85 | 4.00 | 2.51/1 |
| 57188.756~57188.880 | 0.39 | 0.173 | 30.0 | 0.68 | 0.29 | 330 | 1.00 × 106 | 1.10 × 103 | 1.95 | 4.00 | 28.00/11 |
| 57189.125~57189.250 | 0.13 | 0.140 | 38.0 | 0.63 | 2.30 | 400 | 1.00 × 106 | 1.30 × 103 | 2.05 | 4.00 | 11.98/5 |
| 57189.734~57189.888 | 0.35 | 0.179 | 25.0 | 0.45 | 1.00 | 150 | 1.00 × 106 | 2.10 × 103 | 1.90 | 4.10 | 19.35/11 |
| 56640~56645 | 0.22 | 0.330 | 30.0 | 1.80 | 10.70 | 70 | 1.00 × 105 | 1.30 × 103 | 2.45 | 4.30 | 16.35/19 |
| 56645~56649 | 0.36 | 0.221 | 20.0 | 0.35 | 7.70 | 60 | 1.00 × 105 | 2.20 × 103 | 2.05 | 4.40 | 9.91/16 |
| 56649~56660 | 0.94 | 0.340 | 20.0 | 0.67 | 0.15 | 200 | 1.00 × 106 | 1.30 × 103 | 2.45 | 4.70 | 20.44/26 |
| 56741~56749 | 1.75 | 0.510 | 16.0 | 0.44 | 0.03 | 180 | 1.00 × 105 | 1.00 × 103 | 2.10 | 4.30 | 17.35/16 |
| 56749~56755 | 1.70 | 0.300 | 23.0 | 0.74 | 0.02 | 220 | 5.00 × 104 | 7.00 × 102 | 1.95 | 4.10 | 5.04/17 |
| 56755~56760 | 1.43 | 0.410 | 18.0 | 0.70 | 0.35 | 80 | 1.00 × 106 | 1.50 × 103 | 2.50 | 4.20 | 3.80/15 |
| 55300~55400 | 0.45 | 0.305 | 16.0 | 0.95 | 6.50 | 60 | 1.00 × 106 | 1.50 × 103 | 2.30 | 4.70 | 9.08/15 |
本文统一使用单区轻子模型拟合3C 279的全部29个态的观测数据。本模型中假设辐射区域为半径R的球形,球形区域内充满均匀分布的电子,并以速度βc沿喷流方向运动。喷流方向与我们观测的视向夹角为θ,球形区域的洛伦兹因子为Г=(1-β2)-1/2。由于多普勒效应,观测到的辐射增亮,辐射区与中心黑洞的距离记为r。相对论电子与辐射区内部的磁场作用产生同步辐射,和同步辐射产生的软光子以及吸积盘、宽线区和尘埃环提供的软光子碰撞,产生逆康普顿散射。电子能量分布以拐折幂律谱的形式表示为[43]
| $ \begin{array}{*{20}{l}} {N\left( \gamma \right) = {N_0}{\gamma ^{ - {p_1}}}\left( {{\gamma _{{\rm{min}}}} < \gamma < {\gamma _{\rm{b}}}} \right), }\\ {N\left( \gamma \right) = {N_0}\gamma _{\rm{b}}^{{p_2} - {p_1}}{\gamma ^{ - {p_2}}}\left( {{\gamma _{\rm{b}}} < \gamma < {\gamma _{{\rm{max}}}}} \right), } \end{array} $ | (1) |
其中,N0为归一化系数;γmin和γmax为电子洛伦兹因子γ的最小值和最大值;γb为电子在拐点处洛伦兹因子;p1和p2分别为同步峰左侧和右侧光薄段的谱指数。得到稳态电子能谱分布后,我们使用公共PYTHON软件包NAIMA计算来自喷流的同步加速辐射、同步自康普顿(Synchrotron Self-Compton, SSC) 辐射和外康普顿辐射[44]。
目前,单区模型依然应用广泛[39, 45]。使用单区均匀轻子模型对耀变体的光变态光谱能量分布进行拟合,一方面可以得到各态内在物理参数包括辐射区所在位置的磁场、描述运动的多普勒因子和描述发出辐射的电子集的电子能谱分布特性参数等[22],而且在较大样本条件下使用同一个模型进行拟合后,可以对物理性质进行统计分析,从而对比得到不同态下源的物理特性;另一方面还可以利用拟合结果对前述三种可能的模型进行检验。
2.2 拟合结果我们拟合使用的样本及模型参数见表 1,光谱能量分布见图 1~图 4。拟合结果表明,拐折幂律谱电子能谱分布的稳态单区均匀轻子模型能够较理想地拟合29个包含光学、X射线和γ射线波段在内的光谱能量分布观测数据。
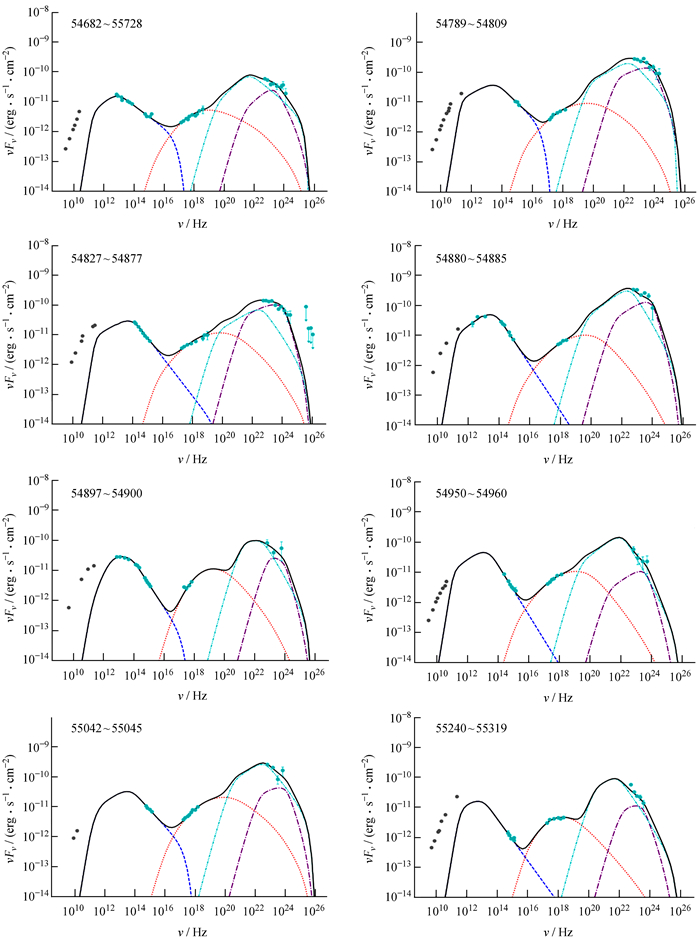
|
| 图 1 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(1~8),其中,蓝色虚线表示同步辐射过程,红色虚线表示同步自康普顿过程,青色虚线表示外康普顿/尘埃环,紫色虚线表示外康普顿/宽线区,黑色实线表示总的拟合线 Fig. 1 The one-zone homogeneous lepton model is fitted to the SED data figure (1-8) observed by 3C 279, where blue dotted line represents synchrotron radiation process, red dotted line represents synchrotron self-Compton process, cyan dotted line represents EC/DT, purple dotted line represents EC/BLR, and black solid line represents the total fitting line |
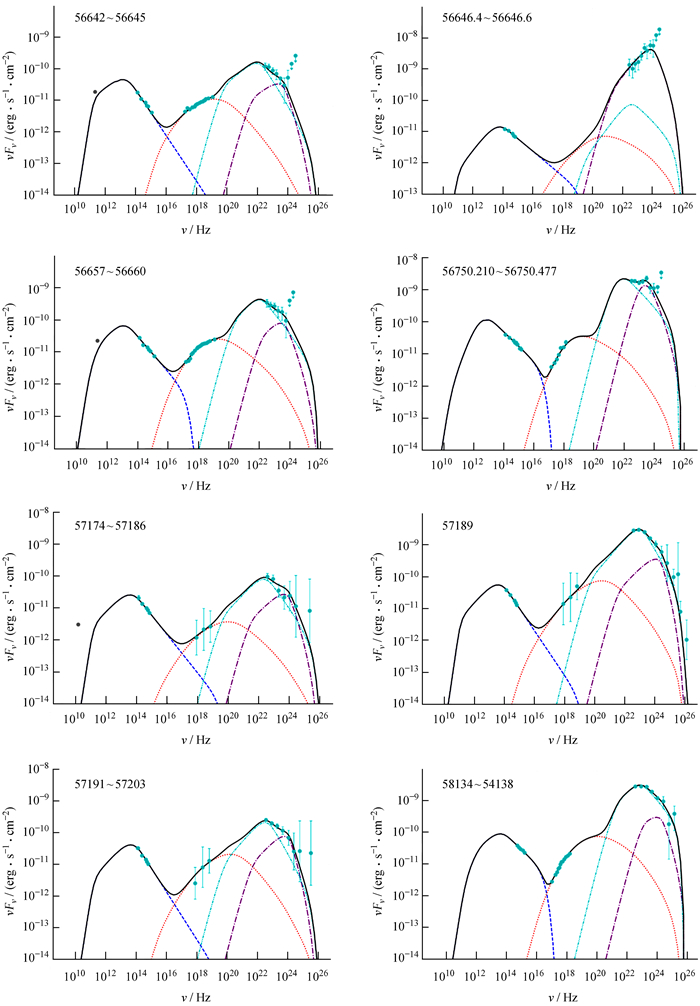
|
| 图 2 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(9~16) Fig. 2 The one-zone homogeneous lepton model is fitted to the SED data figure (9-16) observed by 3C 279 |
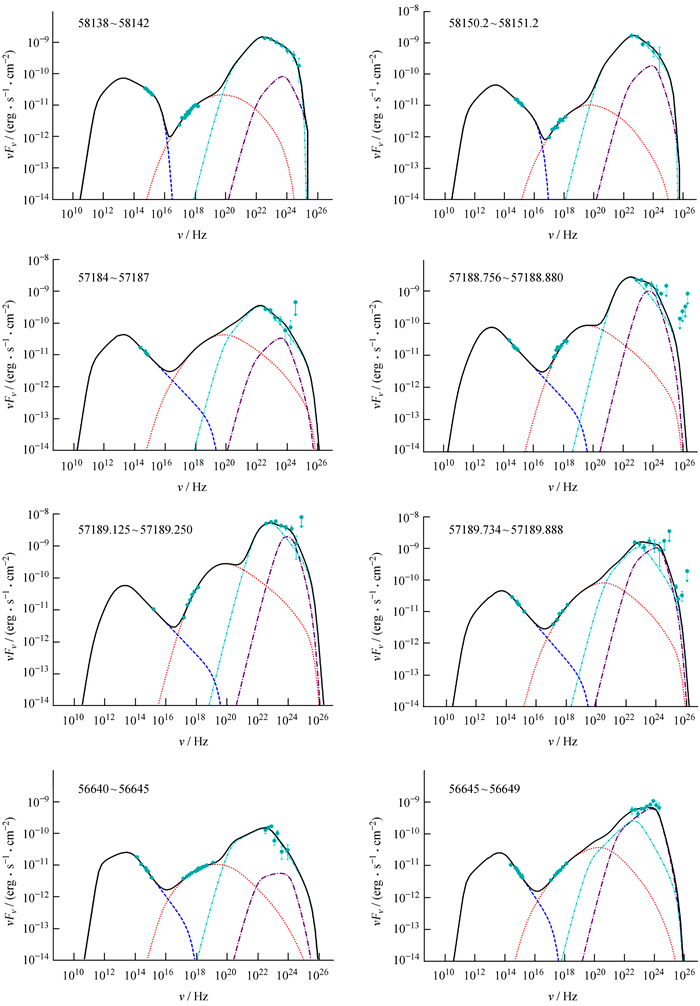
|
| 图 3 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(17~24) Fig. 3 The one-zone homogeneous lepton model is fitted to the SED data figure (17-24) observed by 3C 279 |
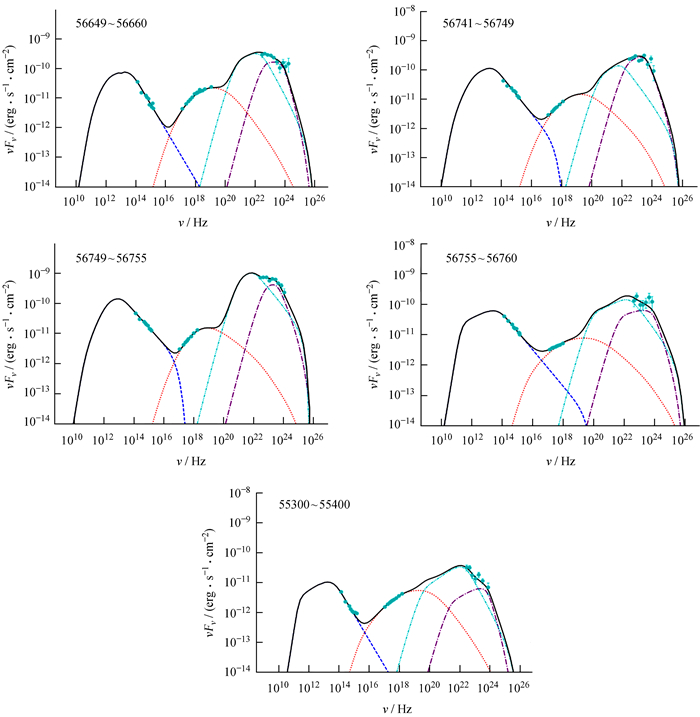
|
| 图 4 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(25~29) Fig. 4 The one-zone homogeneous lepton model is fitted to the SED data figure (25-29) observed by 3C 279 |
在我们的拟合结果中,辐射区半径R的范围为1.3×1016~2.2×1017cm,与文[42]的结果一致。磁感应强度B的范围为0.103~0.51 G,与文[46]的结果一致。多普勒因子δ的范围为14~38.44,与文[46]的结果一致。
由于激波和磁重联机制产生的电子能谱分布各有特点:在电子能谱分布形如ne(γ)∝γ-p时,一般相对论性平行激波产生的电子能谱分布谱指数在p~2.2附近[47-50]。如果是相对论性的斜激波,也可能产生谱形较硬的电子能谱分布,p
同步峰的峰值频率和峰值光度的范围(峰值频率对数的均值为13.34,标准差为0.27;峰值光度的均值为46.66,标准差为0.28)比外康普顿峰的(峰值频率对数的均值为22.48,标准差为0.53;峰值光度的均值为47.69,标准差为0.60) 小,这意味着无论是从频率还是光度对比,同步辐射的光变幅度都明显比外康普顿辐射的低,而且这个特性还导致一个相关性的产生。
在外康普顿峰值光度logνECpkLECpk和磁场logB之间,存在一个显著的反相关关系(r=-0.70,p < 1.95× 10-5)。根据前述性质可以有如下解释:首先外康普顿峰的峰值频率logνECpk和峰值光度logνECpkLECpk之间存在一个显著的正相关(r=0.55,p < 0.002 2),这意味着当νECpkLECpk升高时,νECpk随之升高。如果近似认为外康普顿光度由来自宽线区或者尘埃环中的某个成分主导,根据νECpk ~ ν*δ2γb2 (ν*是主导成分软光子的特征频率),δ2γb2升高。另一方面,由于同步峰的峰值频率在一个较窄的范围内波动,考虑到νsynpk ~ Bδγb2,显然在νECpkLECpk升高时,磁场B有降低的趋势。这同时意味着γ射线波段耀发时,伴随外康普顿光度的升高,康普顿主导(Compton Dominance, CD) 增加,而同步冷却的相对重要性却在降低,所以更大比例的能量通过外康普顿冷却在γ射线波段辐射。
另外,关于多普勒因子δ和外康普顿峰的峰值光度νECpkLECpk的相关性,有人认为外康普顿峰的峰值光度νECpkLECpk升高的一部分原因是由于多普勒因子δ增加。文[31]在用Mrk 501和3C 279研究耀变体反序列时发现,3C 279外康普顿峰的峰值光度νECpkLECpk∝δ6.20±1.70,多普勒因子是外康普顿峰的峰值光度变化的重要原因。文[53]在研究GeV NLS1星系与3C 279是否存在相同的关系时,得到3C 279的外康普顿峰的峰值光度νECpkLECpk∝δ7.65±2.74,也表明多普勒因子增加是外康普顿峰的峰值光度升高的一部分原因。同样的,文[54]在研究GeV窄线Seyfert 1星系与平谱射电类耀变体喷流的相似性时发现,平谱射电类耀变体的外康普顿峰的峰值光度与多普勒因子之间存在一种普遍的相关性。
为了进一步验证外康普顿峰的峰值光度与多普勒因子之间是否存在相关性,本文对样本参数中的外康普顿峰的峰值光度和多普勒因子进行了相关性分析,得到logνECpkLECpk与logδ之间存在正相关关系:logνECpkLECpk=(3.97±0.82)logδ+(42.38±1.10) (r=0.53,p < 3.00×10-3)。相比文[54]研究的外康普顿峰的峰值光度与多普勒因子之间的关系为logνECpkLECpk=(5.45±0.33) logδ+(41.11±0.39) (r=0.93,p < 1.80×10-6),我们的结果与文[54]的一致,都呈现正相关,说明多普勒因子增加是外康普顿峰的峰值光度升高的原因之一。但本文结果的斜率略低,由于本文所使用的模型和文[54]是一致的,但外康普顿过程中的软光子来源不同,文[54]外康普顿过程的软光子全部来源于宽线区,本文外康普顿过程的软光子主要来自尘埃环,所以这可能是导致斜率不同的原因之一。
对于是否一次耀发是由几何因素的变化导致的(比如存在弯曲或者螺线型的喷流路径,必然导致辐射区在不同时间或不同位置时具有不同的多普勒因子,从而产生不同的多普勒增亮),这可以直接通过单区均匀模型对不同态的拟合进行检验[16]。根据拟合结果,在logδ和logνsynpkLsynpk之间不存在显著相关性(r=-0.25,p < 0.20)。而在logδ和logνECpkLECpk之间存在显著相关性(r=-0.53,p < 0.003 0)。考虑到在单区模型中,同步和外康普顿两个辐射区是共空间的,这意味着在3C 279的光变过程中,并不存在一个简单的几何效应解释。
3.2 同步峰的峰值频率和峰值光度的相关性耀变体序列是耀变体研究中一个重要而富有争议的问题[55-56]。因为观测的耀变体的光谱能量分布图(logν -logνF(ν))中有同步峰和逆康普顿(Inverse Compton, IC) 两个辐射成分,所以最早版本的耀变体序列[57]研究不同的源(一般每个源用某一个态表示) 同步峰的峰值频率和峰值光度之间的关系。由于不同的源中心黑洞、喷流物理性质和喷流周围环境不同,最终导致不同的源在峰值光度-峰值频率平面上的不同分布。但是对于同一个源来说不存在黑洞、喷流和环境几个方面的差异,可以预期同步峰的峰值频率-峰值光度关系应该和耀变体序列有不同的趋势。文[58]发现高峰频BL Lac源Mrk 421在光变时,X射线波段的同步峰的峰值频率和峰值光度之间有一个显著的正相关关系。这个相关性解释为相对论性电子同步辐射的特征。文[59]进一步研究了5个高峰频BL Lac源,发现其中4个也显示了和Mrk 421一样的正相关性。文[31]在高峰频BL Lac源Mrk 501和平谱射电类星体3C 279的4个态中都发现了上述相关性,于是推测在所有耀变体中这个相关性存在。加之这个相关性和耀变体序列描述的反相关性相反,于是称之为“反耀变体序列”。本文也对此进行了研究。同步峰的峰值频率-峰值光度的相关性分析给出:皮尔逊(Pearson) 相关系数r=-0.145 1,p=0.452 6,说明3C 279在光变时,logνsynpk-logνsynpkLsynpk之间不存在显著的正相关关系。所以我们的结果表明,文[31]的结果可能是选择效应导致的,反耀变体序列不一定对所有耀变体成立。
在单区模型中,使用单色近似可以得到关于同步峰的峰值频率和峰值光度的关系:νsynpkLsynpk∝Nγb2B2δ4和νsynpk∝γb2Bδ。如果νsynpkLsynpk∝νsynpk,则γb的变化主导光变;如果νsynpkLsynpk∝ (νsynpk) 2,则磁场B的变化主导光变[31, 58]。所以没有显著的正相关说明在3C 279的各光变态中不存在唯一的主导因素。这要么意味着导致光变的物理因素有多个,从而无法确定主导因素;要么意味着不同时间的光变过程中存在不同的主导因素,从而导致一个显著相关性的缺失。
3.3 喷流的物理性质及辐射区位置喷流功率对于我们了解喷流的产生和组成至关重要,我们可以通过光谱能量分布拟合参数估算喷流功率。通常假设喷流功率是由相对论电子、冷质子、磁场和辐射携带[41]:
| $ {P_{{\rm{jet}}}} = {\rm{ \mathsf{ π} }}{R^2}{\mathit{\Gamma }^2}c({U_{\rm{e}}} + {U_{\rm{p}}} + {U_{\rm{B}}} + {U_{\rm{r}}}), $ | (2) |
其中,Ue为相对论电子能量密度;Up为冷质子能量密度;UB为磁场能量密度;Ur为辐射能量密度,其计算公式为
| $ {U_{\rm{e}}} = {m_{\rm{e}}}{c^2}\smallint N\left( \gamma \right)\gamma {\rm{d}}\gamma , $ | (3) |
| $ {U_{\rm{p}}} = {m_{\rm{p}}}{c^2}\smallint N\left( \gamma \right){\rm{d}}\gamma , $ | (4) |
| $ {U_{\rm{B}}} = \frac{{{B^2}}}{{8{\rm{ \mathsf{ π} }}}}, $ | (5) |
| $ {U_{\rm{r}}} = \frac{{{L_{{\rm{obs}}}}}}{{4{\rm{ \mathsf{ π} }}{R^2}c{\delta ^4}}}, $ | (6) |
(6) 式中,Lobs为观测到的总非热辐射光度,Lobs=4πDL2F (DL为光度距离,F为观测流量)。计算得到的参数见表 2。表 2中每列的详细信息如下:第1列为样本观测时间;第2列为相对论电子能量密度;第3列为磁场能量密度;第4列为相对论电子功率;第5列为冷质子功率;第6列为磁场功率;第7列为辐射功率;第8列为喷流总功率;第9列为相对论电子能量密度与磁场能量密度的比值。
| Time period (MJD) (1) |
Ue/(erg·cm-3) (2) |
UB/(erg·cm-3) (3) |
Pe/(erg·s-1) (4) |
Pp/(erg·s-1) (5) |
PB/(erg·s-1) (6) |
Pr/(erg·s-1) (7) |
Pjet/(erg·s-1) (8) |
Ue/UB (9) |
| 54682~55728 | 1.73 × 10-2 | 3.01 × 10-3 | 2.18 × 1045 | 2.05 × 1046 | 3.79 × 1044 | 5.77 × 1044 | 2.36 × 1046 | 5.76 |
| 54789~54809 | 9.77 × 10-3 | 3.58 × 10-3 | 2.79 × 1045 | 3.10 × 1046 | 1.02 × 1045 | 1.48 × 1045 | 3.63 × 1046 | 2.73 |
| 54827~54877 | 3.48 × 10-2 | 8.24 × 10-3 | 2.00 × 1045 | 2.20 × 1046 | 4.72 × 1044 | 8.02 × 1044 | 2.53 × 1046 | 4.23 |
| 54880~54885 | 5.85 × 10-3 | 3.12 × 10-3 | 2.55 × 1045 | 2.46 × 1046 | 1.36 × 1045 | 1.61 × 1045 | 3.01 × 1046 | 1.88 |
| 54897~54900 | 5.08 × 10-2 | 9.95 × 10-3 | 1.16 × 1045 | 4.65 × 1045 | 2.26 × 1044 | 2.65 × 1044 | 6.29 × 1045 | 5.11 |
| 54950~54960 | 3.71 × 10-3 | 2.49 × 10-3 | 3.32 × 1045 | 3.30 × 1046 | 2.22 × 1045 | 1.41 × 1045 | 4.00 × 1046 | 1.49 |
| 55042~55045 | 2.00 × 10-2 | 2.29 × 10-3 | 2.81 × 1045 | 1.31 × 1046 | 3.21 × 1044 | 1.29 × 1045 | 1.75 × 1046 | 8.74 |
| 55240~55319 | 5.07 × 10-2 | 4.87 × 10-3 | 2.02 × 1045 | 1.64 × 1046 | 1.94 × 1044 | 2.40 × 1044 | 1.89 × 1046 | 10.40 |
| 56642~56645 | 6.10 × 10-3 | 3.95 × 10-3 | 2.44 × 1045 | 1.96 × 1046 | 1.58 × 1045 | 1.13 × 1045 | 2.47 × 1046 | 1.55 |
| 56646.4~56646.6 | 1.10 × 10-2 | 2.69 × 10-3 | 9.09 × 1044 | 4.68 × 1045 | 2.21 × 1044 | 1.50 × 1046 | 2.08 × 1046 | 4.10 |
| 56657~56660 | 5.39 × 10-3 | 2.10 × 10-3 | 3.30 × 1045 | 1.42 × 1046 | 1.29 × 1045 | 2.53 × 1045 | 2.13 × 1046 | 2.56 |
| 56750.210~56750.477 | 2.78 × 10-3 | 1.16 × 10-3 | 4.16 × 1045 | 1.12 × 1046 | 1.74 × 1045 | 8.31 × 1045 | 2.54 × 1046 | 2.39 |
| 57174~57186 | 4.49 × 10-3 | 5.60 × 10-3 | 8.82 × 1044 | 7.02 × 1045 | 1.10 × 1045 | 4.81 × 1044 | 9.48 × 1045 | 0.80 |
| 57189 | 2.01 × 10-2 | 4.22 × 10-4 | 8.61 × 1045 | 5.45 × 1046 | 1.81 × 1044 | 8.41 × 1045 | 7.18 × 1046 | 47.58 |
| 57191~57203 | 1.46 × 10-2 | 3.46 × 10-3 | 1.97 × 1045 | 1.12 × 1046 | 4.67 × 1044 | 1.13 × 1045 | 1.47 × 1046 | 4.22 |
| 58134~58138 | 5.49 × 10-2 | 1.94 × 10-3 | 4.78 × 1045 | 1.65 × 1046 | 1.69 × 1044 | 2.92 × 1045 | 2.43 × 1046 | 28.27 |
| 58138~58142 | 2.21 × 10-2 | 2.71 × 10-3 | 3.56 × 1045 | 2.71 × 1046 | 4.36 × 1044 | 1.59 × 1045 | 3.27 × 1046 | 8.16 |
| 58150.2~58151.2 | 1.55 × 10-2 | 1.84 × 10-3 | 2.58 × 1045 | 1.60 × 1046 | 3.05 × 1044 | 1.59 × 1045 | 2.05 × 1046 | 8.45 |
| 57184~57187 | 1.67 × 10-2 | 1.44 × 10-3 | 4.45 × 1045 | 2.18 × 1046 | 3.82 × 1044 | 2.41 × 1045 | 2.91 × 1046 | 11.66 |
| 57188.756~57188.880 | 4.58 × 10-2 | 1.19 × 10-3 | 5.91 × 1045 | 1.53 × 1046 | 1.54 × 1044 | 4.63 × 1045 | 2.60 × 1046 | 38.47 |
| 57189.125~57189.250 | 4.87 × 10-1 | 7.80 × 10-4 | 1.12 × 1046 | 2.46 × 1046 | 1.79 × 1043 | 5.37 × 1045 | 4.11 × 1046 | 624.29 |
| 57189.734~57189.888 | 6.70 × 10-2 | 1.28 × 10-3 | 4.83 × 1045 | 1.69 × 1046 | 9.20 × 1043 | 4.15 × 1045 | 2.59 × 1046 | 52.48 |
| 56640~56645 | 7.48 × 10-2 | 4.34 × 10-3 | 3.01 × 1045 | 3.10 × 1046 | 1.75 × 1044 | 3.16 × 1044 | 3.45 × 1046 | 17.25 |
| 56645~56649 | 8.27 × 10-2 | 1.94 × 10-3 | 4.04 × 1045 | 3.18 × 1046 | 9.49E+43 | 2.83 × 1045 | 3.87 × 1046 | 42.56 |
| 56649~56660 | 7.00 × 10-3 | 4.60 × 10-3 | 2.33 × 1045 | 9.94 × 1045 | 1.53 × 1045 | 1.72 × 1045 | 1.55 × 1046 | 1.52 |
| 56741~56749 | 1.70 × 10-3 | 1.03 × 10-2 | 1.26 × 1045 | 5.39 × 1045 | 7.64 × 1045 | 2.37 × 1045 | 1.67 × 1046 | 0.16 |
| 56749~56755 | 1.55 × 10-3 | 3.58 × 10-3 | 2.23 × 1045 | 8.87 × 1045 | 5.16 × 1045 | 3.20 × 1045 | 1.95 × 1046 | 0.43 |
| 56755~56760 | 3.01 × 10-3 | 6.69 × 10-3 | 1.88 × 1045 | 1.74 × 1046 | 4.17 × 1045 | 1.33 × 1045 | 2.48 × 1046 | 0.45 |
| 55300~55400 | 4.22 × 10-2 | 3.70 × 10-3 | 2.06 × 1045 | 2.18 × 1046 | 1.81 × 1044 | 3.06 × 1044 | 2.44 × 1046 | 11.41 |
文[38]分析了3C 279在MJD 58129~58152时段的三个态,得到在两种γ射线辐射模型下,Ue和UB接近均分以及2018年1月的γ射线耀发外康普顿过程中的软光子是由尘埃环提供。文[39]分析了3C 279在MJD 57174~57203时段的三个态,得到在低态时粒子的能量密度和磁场能量密度接近均分,在耀发时这两者远离均分,表明喷流以粒子或物质主导的结论,并且指明造成耀发的可能原因是辐射区电子密度增加和耀发时辐射区小于低态的辐射区。参数Ue/UB的比值基本上远离1,所以两者之间均分的趋势不明显。同时从参数Ue/UB可以得到比值大于1的占86%,小于1的占14%,本文的研究表明3C 279中的喷流多数以粒子为主导,这与文[41], 60-61]的研究结果一致。
根据表 2中的样本参数计算的每种成分所携带能量占总能量的比值,结果见表 3。通过表 3我们发现PB < Pr < Pe < Pp,与文[62]的结果定性一致。其中Pe > PB表明磁场功率与相对论电子功率之间均分的趋势不明显,与我们得到Ue和UB之间的结论相同,也进一步说明喷流以粒子主导,这与之前的许多研究结果一致[41, 60-61]。文[63]指出BL Lac中大多数源的喷流能量由冷质子携带,本文中Pp/Pjet > 0.5表明3C 279喷流中的能量大概率也是由冷质子携带的。PB < Pr意味着坡印廷(Poynting) 通量不能解释辐射功率,与文[42]的研究结果一致。Pr/Pe约为0.1~1.9,这表明相对论电子功率的很大一部分用于产生观测到的辐射,与文[42]的研究结果一致。
| Pe/Pjet | Pp/Pjet | PB/Pjet | Pr/Pjet |
| 0.125 | 0.710 | 0.057 | 0.108 |
同时,我们根据文[60]中xBLR=0.1(Ld/1046erg-s)1/2pc和xDT=2.5(Ld/1046erg-s)1/2pc两个公式可以计算宽线区和尘埃环的特征位置,分别为xBLR=0.078pc和xDT=1.940pc。由表 1可知,在我们的模型中γ射线耗散区位于0.1~1.8 pc的范围内,这意味着它们位于宽线区之外,尘埃环之内。从我们拟合结果中MJD 54827~54877,MJD 56646.4~56646.6和MJD 56741~56749时段的数据可以直观地看出,外康普顿过程的软光子以宽线区为主导,而其余26个态的外康普顿过程中的软光子以尘埃环为主导。因此,我们发现γ射线的辐射区一般位于宽线区之外,并且平谱射电类星体3C 279的外康普顿过程的软光子受尘埃环的影响较大。本文的结果与文[64]-67]的研究成果一致,由于本文样本中同时/准同时性数据的辐射区位置相对分散,因此本文的结果更倾向于耗散区在宽线区之外。
4 结论本文基于稳态单区均匀轻子模型对29个态的同时/准同时性光谱能量分布数据的拟合,研究了平谱射电类星体3C 279的物理特性。主要结论如下:
(1) 我们通过拟合参数中电子谱指数的范围与前人理论中的范围对比发现,本文的结果支持光变的激波解释(但需要斜激波) 或磁重联解释。
(2) 在拟合参数中发现两个相关性,外康普顿峰的峰值光度logνECpkLECpk和磁场logB之间存在一个显著的反相关关系。多普勒因子logδ和外康普顿峰的峰值光度logνECpkLECpk之间存在一个正相关关系,意味着多普勒因子增加是外康普顿峰的峰值光度升高的原因之一。
(3) 同步峰的峰值频率和峰值光度之间的相关性一直用于反耀变体序列的研究。在本文的样本参数中发现两者之间不存在显著的正相关关系,这暗示了反耀变体序列不一定对所有的耀变体成立。
(4) 在本文拟合参数中Ue/UB的比值基本上远离1,所以两者之间均分的趋势不明显。同时参数Ue/UB的比值大于1的占86%,表明3C 279中的喷流多数以粒子为主导。我们发现PB < Pr < Pe < Pp这一关系,Pp/Pjet>0.5表明3C 279喷流中的能量大概率也是由冷质子携带的。Pr/Pe约为0.1~ 1.9表明相对论电子功率的很大一部分用于产生观测到的辐射。同时,我们发现3C 279中γ射线耗散区位于0.1~1.8 pc,暗示着它们位于宽线区之外,尘埃环之内。
| [1] | URRY C M, PADOVANI P. Unified schemes for radio-loud active galactic nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107(715): 803–845. |
| [2] | BÖTTCHER M. Progress in multi-wavelength and multi-messenger observations of blazars and theoretical challenges[J]. Galaxies, 2019, 7(1): 20. DOI: 10.3390/galaxies7010020 |
| [3] | MARSCHER A P, GEAR W K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273[J]. The Astrophysical Journal, 1985, 298(1): 114–127. |
| [4] | GRAFF P B, GEORGANOPOULOS M, PERLMAN E S, et al. A multi-zone model for simulating the high energy variability of TeV blazars[J]. The Astrophysical Journal, 2008, 689(1): 68–78. DOI: 10.1086/592427 |
| [5] | BOTTCHER M, DERMER C D. Timing signatures of the internal-shock model for blazars[J]. The Astrophysical Journal, 2010, 711(1): 445–460. DOI: 10.1088/0004-637X/711/1/445 |
| [6] | CHEN X, FOSSATI G, LIANG E P, et al. Time-dependent simulations of multiwavelength variability of the blazar Mrk 421 with a Monte Carlo multizone code[J]. Monthly Notices of the Royal Astronomical Society, 2011, 416(3): 2368–2387. DOI: 10.1111/j.1365-2966.2011.19215.x |
| [7] | KAGAN D, SIRONI L, CERYTTI B, et al. Relativistic magnetic reconnection in pair plasmas and its astrophysical applications[J]. Space Science Reviews, 2015, 191(1): 545–573. |
| [8] | NALEWAJKO K, UZDENSKY D A, CERUTTI B, et al. On the distribution of particle acceleration sites in plasmoid-dominated relativistic magnetic reconnection[J]. The Astrophysical Journal, 2015, 815(2): 101. DOI: 10.1088/0004-637X/815/2/101 |
| [9] | SIRON L, PETROPOULOU M, GIANNIOS D. Relativistic jets shine through shocks or magnetic reconnection?[J]. Monthly Notices of the Royal Astronomical Society, 2015, 450(1): 183–191. DOI: 10.1093/mnras/stv641 |
| [10] | GUO F, LI X, LI H, et al. Efficient production of high-energy nonthermal particles during magnetic reconnection in a magnetically dominated ion-electron plasma[J]. The Astrophysical Journal Letters, 2016, 818(1): L9. DOI: 10.3847/2041-8205/818/1/L9 |
| [11] | WERNER G R, UZDENSKY D A, CERUTTI B, et al. The extent of power-law energy spectra in collisionless relativistic magnetic reconnection in pair plasmas[J]. The Astrophysical Journal Letters, 2015, 816(1): L8. DOI: 10.3847/2041-8205/816/1/L8 |
| [12] | GUO F, LI H, DAUGHTON W, et al. Formation of hard power laws in the energetic particle spectra resulting from relativistic magnetic reconnection[J]. Physical Review Letters, 2014, 113(15): 155005. DOI: 10.1103/PhysRevLett.113.155005 |
| [13] | VILLATA M, RAITERI C M. Helical jets in blazars. Ⅰ. the case of MKN 501[J]. Astronomy & Astrophysics, 1999, 347: 30–36. |
| [14] | LARIONOV V M, JORSTAD S G, MARSCHER A P, et al. The outburst of the blazar S5 0716+71 in 2011 October: shock in a helical jet[J]. The Astrophysical Journal, 2013, 768(1): 40. DOI: 10.1088/0004-637X/768/1/40 |
| [15] | LARIONOV V M, VILLATA M, RAITERI C M, et al. Exceptional outburst of the blazar CTA 102 in 2012: the GASP-WEBT campaign and its extension[J]. Monthly Notices of the Royal Astronomical Society, 2016, 461(3): 3047–3056. DOI: 10.1093/mnras/stw1516 |
| [16] | RAITERI C M, VILLATA M, ACOSTA-PULIDO J A, et al. Blazar spectral variability as explained by a twisted inhomogeneous jet[J]. Nature, 2017, 552(7685): 374–377. DOI: 10.1038/nature24623 |
| [17] | ARAUDO A T, BOSCH-RAMON V, ROMERO G E. Gamma rays from cloud penetration at the base of AGN jets[J]. Astronomy & Astrophysics, 2010, 522: A97. |
| [18] | BARKOV M V, AHARONIAN F A, BOSCH-RAMON V. Gamma-ray flares from red giant/jet interactions in active galactic nuclei[J]. The Astrophysical Journal, 2010, 724(2): 1517. DOI: 10.1088/0004-637X/724/2/1517 |
| [19] | KHANGULYAN D V, BARKOV M V, BOSCH-RAMON V, et al. Star-jet interactions and gamma-ray outbursts from 3C454. 3[J]. The Astrophysical Journal, 2013, 774(2): 113. DOI: 10.1088/0004-637X/774/2/113 |
| [20] | RYAN J L, SIEMIGINOWSKA A, SOBOLEWSKA M A, et al. Characteristic variability timescales in the gamma-ray power spectra of blazars[J]. The Astrophysical Journal, 2019, 885(1): 12. DOI: 10.3847/1538-4357/ab426a |
| [21] | RAITERI C M, VILLATA M, LARIONOV V M, et al. The complex variability of blazars: time-scales and periodicity analysis in S4 0954+65[J]. Monthly Notices of the Royal Astronomical Society, 2021, 504(4): 5629–5646. DOI: 10.1093/mnras/stab1268 |
| [22] | ALEKSICĆ J, ALVAREZ E A, ANTONELLI L A, et al. Mrk 421 active state in 2008: the MAGIC view, simultaneous multi-wavelength observations and SSC model constrained[J]. Astronomy & Astrophysics, 2012, 542: A100. |
| [23] | HARTMAN R C, BERTSCH D L, FICHTEL C E, et al. Detection of high-energy gamma radiation from quasar 3C 279 by the EGRET telescope on the Compton Gamma Ray Observatory[J]. The Astrophysical Journal, 1992, 385: L1–L4. DOI: 10.1086/186263 |
| [24] | KNIFFEN D A, BERTSCH D L, FICHTEL C E, et al. Time variability in the gamma-ray emission of 3C 279[J]. The Astrophysical Journal, 1993, 411: 133–136. DOI: 10.1086/172813 |
| [25] | WEHRLE A E, PIAN E, URRY C M, et al. Multiwavelength observations of a dramatic high-energy flare in the blazar 3C 279[J]. The Astrophysical Journal, 1998, 497(1): 178. DOI: 10.1086/305461 |
| [26] | ALBERT J, ALIU E, ANDERHUB H, et al. Very-high-energy gamma rays from a distant quasar: how transparent is the universe?[J]. Science, 2008, 320(5884): 1752–1754. DOI: 10.1126/science.1157087 |
| [27] | ACKERMANN M, ANANTUA R, ASANO K, et al. Minute-timescale> 100 MeV gamma-ray variability during the giant outburst of quasar 3C 279 observed by Fermi-LAT in 2015 June[J]. The Astrophysical Journal Letters, 2016, 824(2): L20. DOI: 10.3847/2041-8205/824/2/L20 |
| [28] | KIM J Y, KRICHBAUM T P, BRODERICK A E, et al. Event Horizon Telescope imaging of the archetypal blazar 3C 279 at an extreme 20 microarcsecond resolution[J]. Astronomy & Astrophysics, 2020, 640: A69. |
| [29] | WENDEL C, SHUKLA A, MANNHEIM K. Pair cascades at the edge of the broad-line region shaping the gamma-ray spectrum of 3C 279[J]. The Astrophysical Journal, 2021, 917(1): 32. DOI: 10.3847/1538-4357/ac0a6e |
| [30] | HAYASHIDA M, MADEJSKI G M, NALEWAJKO K, et al. The structure and emission model of the relativistic jet in the Quasar 3C 279 inferred from radio to high-energy gamma-ray observations in 2008-2010[J]. The Astrophysical Journal, 2012, 754(2): 114. DOI: 10.1088/0004-637X/754/2/114 |
| [31] | ZHANG J, ZHANG S N, LIANG E W. Blazar anti-sequence of spectral variation within individual blazars: cases for Mrk 501 and 3C 279[J]. The Astrophysical Journal, 2013, 767(1): 8. DOI: 10.1088/0004-637X/767/1/8 |
| [32] | HAYASHIDA M, NALEWAJKO K, MADEJSKI G M, et al. Rapid variability of blazar 3C 279 during flaring states in 2013-2014 with joint Fermi-LAT, NuSTAR, Swift, and ground-based multi-wavelength observations[J]. The Astrophysical Journal, 2015, 807(1): 79. DOI: 10.1088/0004-637X/807/1/79 |
| [33] | HU W, YAN D, DAI B, et al. On the injection of relativistic electrons in the jet of 3C 279[J]. Monthly Notices of the Royal Astronomical Society, 2020, 493(1): 410–426. DOI: 10.1093/mnras/staa264 |
| [34] | SHUKLA A, MANNHEIM K. Gamma-ray flares from relativistic magnetic reconnection in the jet of the quasar 3C 279[J]. Nature Communications, 2020, 11(1): 1–8. DOI: 10.1038/s41467-019-13993-7 |
| [35] | PALIYA V S, SAHAYANATHAN S, STALIN C S. Multi-wavelength observations of 3C 279 during the extremely bright gamma-ray flare in 2014 March-April[J]. The Astrophysical Journal, 2015, 803(1): 15. DOI: 10.1088/0004-637X/803/1/15 |
| [36] | PALIYA V S, DILTZ C, BÖTTCHER M, et al. A hard gamma-ray flare from 3C 279 in 2013 December[J]. The Astrophysical Journal, 2016, 817(1): 61. DOI: 10.3847/0004-637X/817/1/61 |
| [37] | ABDALLA H, ADAM R, AHARONIAN F, et al. Constraints on the emission region of 3C 279 during strong flares in 2014 and 2015 through VHE gamma-ray observations with HESS[J]. Astronomy & Astrophysics, 2019, 627: A159. |
| [38] | SHAH Z, JITHESH V, SAHAYANATHAN S, et al. Study on temporal and spectral behaviour of 3C 279 during 2018 January flare[J]. Monthly Notices of the Royal Astronomical Society, 2019, 484(3): 3168–3179. DOI: 10.1093/mnras/stz151 |
| [39] | SINGH K K, MEINTJES P J, RAMAMONJISOA F A. Understanding the giant gamma-ray outburst on June 16, 2015 from the blazar 3C 279[J]. Astrophysics and Space Science, 2020, 365(2): 1–11. |
| [40] | GHISELLINI G, TAVECCHIO F, GHIRLANDA G. Jet and accretion power in the most powerful Fermi blazars[J]. Monthly Notices of the Royal Astronomical Society, 2009, 399(4): 2041–2054. DOI: 10.1111/j.1365-2966.2009.15397.x |
| [41] | GHISELLINI G, TAVECCHIO F, FOSCHINI L, et al. General physical properties of bright Fermi blazars[J]. Monthly Notices of the Royal Astronomical Society, 2010, 402(1): 497–518. DOI: 10.1111/j.1365-2966.2009.15898.x |
| [42] | TAN C, XUE R, DU L M, et al. The physical properties of Fermi-4LAC flat spectrum radio quasars[J]. The Astrophysical Journal Supplement Series, 2020, 248(2): 27. DOI: 10.3847/1538-4365/ab8cc6 |
| [43] | KANG S J, CHEN L, WU Q. Constraints on the minimum electron Lorentz factor and matter content of jets for a sample of bright Fermi blazars[J]. The Astrophysical Journal Supplement Series, 2014, 215(1): 5. DOI: 10.1088/0067-0049/215/1/5 |
| [44] | ZABALZA V. Naima: a Python package for inference of particle distribution properties from nonthermal spectra[C]//The 34th International Cosmic Ray Conference. 2016. |
| [45] | ROY A, PATEL S R, SARKAR A, et al. Multiwavelength study of the quiescent states of six brightest flat-spectrum radio quasars detected by Fermi-LAT[J]. Monthly Notices of the Royal Astronomical Society, 2021, 504(1): 1103–1114. DOI: 10.1093/mnras/stab975 |
| [46] | DING N, ZHANG X, XIONG D R, et al. The physical properties of Fermi TeV BL Lac objects'jets[J]. Monthly Notices of the Royal Astronomical Society, 2017, 464(1): 599–612. DOI: 10.1093/mnras/stw2347 |
| [47] | BARING M G, ELLISON D C, REYNOLDS S P, et al. Radio to gamma-ray emission from shell-type supernova remnants: predictions from nonlinear shock acceleration models[J]. The Astrophysical Journal, 1999, 513(1): 311. DOI: 10.1086/306829 |
| [48] | KIRK J G, GUTHMANN A W, GALLANT Y A, et al. Particle acceleration at ultrarelativistic shocks: an eigenfunction method[J]. The Astrophysical Journal, 2000, 542(1): 235. DOI: 10.1086/309533 |
| [49] | ACHTERBERG A, GALLANT Y A, KIRK J G, et al. Particle acceleration by ultrarelativistic shocks: theory and simulations[J]. Monthly Notices of the Royal Astronomical Society, 2001, 328(2): 393–408. DOI: 10.1046/j.1365-8711.2001.04851.x |
| [50] | ELLISON D C, DOUBLE G P. Diffusive shock acceleration in unmodified relativistic, oblique shocks[J]. Astroparticle Physics, 2004, 22(3/4): 323–338. |
| [51] | SUMMERLIN E J, BARING M G. Diffusive acceleration of particles at oblique, relativistic, magnetohydrodynamic shocks[J]. The Astrophysical Journal, 2011, 745(1): 127–146. |
| [52] | DING N, GU Q S, GENG X F, et al. Exploring the origin of multiwavelength activities of high-redshift flat-spectrum radio quasar PKS 1502+106 during 2014-2018[J]. The Astrophysical Journal, 2019, 881(2): 125. DOI: 10.3847/1538-4357/ab2f7e |
| [53] | SUN X N, ZHANG J, LIN D B, et al. Jet properties of GeV-selected radio-loud narrow-line Seyfert 1 galaxies and possible connection to their disk and corona[J]. The Astrophysical Journal, 2014, 798(1): 43. DOI: 10.1088/0004-637X/798/1/43 |
| [54] | ZHU Y K, ZHANG J, ZHANG H M, et al. Similarity of jet radiation between flat spectrum radio quasars and GeV narrow-line Seyfert 1 galaxies: a universal δ-L-c correlation[J]. Research in Astronomy and Astrophysics, 2016, 16(11): 170. DOI: 10.1088/1674-4527/16/11/170 |
| [55] | KEENAN M, MEYER E T, GEORGANOPOULOS M, et al. The relativistic jet dichotomy and the end of the blazar sequence[J]. Monthly Notices of the Royal Astronomical Society, 2021, 505(4): 4726–4745. DOI: 10.1093/mnras/stab1182 |
| [56] |
彭瑞, 谢照华, 薛瑞, 等. 费米耀变体峰值参量、康普顿主导、谱指数之间相关性的研究[J]. 天文研究与技术, 2019, 16(4): 401–409 PENG R, XIE Z H, XUE R, et al. The peak information, the Compton dominance, the spectral index diagram, and the correlations for Fermi blazars[J]. Astonomical Research & Technology, 2019, 16(4): 401–409. |
| [57] | FOSSATI G, MARASCHI L, CELOTTI A, et al. A unifying view of the spectral energy distributions of blazars[J]. Monthly Notices of the Royal Astronomical Society, 1998, 299(2): 433–448. DOI: 10.1046/j.1365-8711.1998.01828.x |
| [58] | TRAMACERE A, MASSARO F, CAVALIERE A. Signatures of synchrotron emission and of electron acceleration in the X-ray spectra of Mrk 421[J]. Astronomy & Astrophysics, 2007, 466(2): 521–529. |
| [59] | MASSARO F, TRAMACERE A, CAVALIERE A, et al. X-ray spectral evolution of TeV BL Lacertae objects: eleven years of observations with BeppoSAX, XMM-Newton and Swift satellites[J]. Astronomy & Astrophysics, 2008, 478(2): 395–401. |
| [60] | GHISELLINI G, TAVECCHIO F. The blazar sequence: a new perspective[J]. Monthly Notices of the Royal Astronomical Society, 2008, 387(4): 1669–1680. DOI: 10.1111/j.1365-2966.2008.13360.x |
| [61] | GHISELLINI G, TAVECCHIO F. Fermi/LAT broad emission line blazars[J]. Monthly Notices of the Royal Astronomical Society, 2015, 448(2): 1060–1077. DOI: 10.1093/mnras/stv055 |
| [62] | HU W, YAN D, HU Q. Correlations between gamma-ray luminosity and magnetization of the jet as well as relativistic electron injection power: cases for Mrk 421, 3C 454.3 and 3C 279[J]. Monthly Notices of the Royal Astronomical Society, 2021, 503(2): 2523–2538. DOI: 10.1093/mnras/stab464 |
| [63] | ZHANG J, LIANG E W, ZHANG S N, et al. Radiation mechanisms and physical properties of GeV-TeV BL Lac Objects[J]. The Astrophysical Journal, 2012, 752(2): 157. DOI: 10.1088/0004-637X/752/2/157 |
| [64] | DERMER C D, CERRUTI M, LOTT B, et al. Equipartition gamma-ray blazars and the location of the gamma-ray emission site in 3C 279[J]. The Astrophysical Journal, 2014, 782(2): 82. DOI: 10.1088/0004-637X/782/2/82 |
| [65] | YAN D, ZHANG L, ZHANG S N. Parameter constraints in a near-equipartition model with multifrequency NuSTAR, Swift, and Fermi-LAT data from 3C 279[J]. Monthly Notices of the Royal Astronomical Society, 2015, 454(2): 1310–1319. DOI: 10.1093/mnras/stv2091 |
| [66] | VITTORINI V, TAVANI M, CAVALIERE A. Meeting the challenge from bright and fast gamma-ray flares of 3C 279[J]. The Astrophysical Journal Letters, 2017, 843(2): L23. DOI: 10.3847/2041-8213/aa767f |
| [67] | 黄霞, 马力, 熊定荣, 等. Fermi平谱射电类星体外光子场的研究[J]. 天文研究与技术, 2015, 12(4): 385–393 |



