2. 南京大学天文与空间科学学院, 江苏 南京 210093
2. School of Astronomy & Space Science, Nanjing University, Nanjing 210093, China
耀变体(Blazar) 是观测者视线沿相对论性喷流轴向观测的射电噪活动星系核[1] (Radio-Loud Active Galactic Nuclei) 的一类,包括可以观测到强发射线的平谱射电类星体和观测到弱发射线或者无发射线的蝎虎天体(BL Lacerate, BL lac) 两个子类[2]。观测上,耀变体的宽波段辐射是从射电到伽马射线波段的光谱能量分布(Spectral Energy Distribution, SED),在logv-logvFν图上呈现典型的双峰结构。前人对这种双峰结构进行了大量的研究,目前应用最为广泛的轻子模型认为,低能峰由相对论电子的同步辐射(Synchrotron Radiation, Syn) 产生,高能峰由相对论电子与软光子作用的逆康普顿散射[3] (Inverse Compton scattering, IC) 产生。如果软光子来自同步辐射,称为同步辐射自康普顿模型[4] (Synchrotron Self-Compton, SSC);如果软光子来自喷流外部,称为外康普顿模型(External Compton, EC)。在外康普顿模型下,软光子可能来源于吸积盘[5] (Accretion Disc, AD)、宽线区[6]或尘埃环[7]。到目前为止,逆康普顿散射的软光子来源仍然无法完全确定[8]。
研究认为,耀变体的短时标光变现象意味着产生辐射的位置在宽线区以内[9-10]。标准的单区轻子模型无法解释从平谱射电类星体源3C 279[11],3C 454.3[12]和4C 21.35[13]观测到的甚高能伽马辐射(≥100 GeV) 现象。利用甚长基线干涉技术[14] (Very-Long Baseline Interferometry, VLBI) 对射电辐射的观测发现,在射电波段有一些明亮的区域,这些区域称为射电核,其位置远离中心黑洞,甚至在尘埃环之外[15]。文[16]收集了60个有多波段准同时数据的平谱射电类星体,在单区模型框架下,逆康普顿散射机制中同时考虑宽线区和尘埃环贡献的种子光子,他们发现平谱射电类星体的高能辐射来源于宽线区之外、尘埃环之内。文[17]收集了62个有多波段准同时数据的平谱射电类星体,在轻子模型框架下引入一个参量,基于观测到的多波段光谱能量分布计算双峰结构的峰值频率和通量,确定耀变体中逆康普顿散射机制下外康普顿过程中主要的软光子场,他们把这个参量称为种子因子。结合运用自举法发现,观测的种子因子与期望来自尘埃环的种子因子在统计上显著一致,与期望的宽线区不一致。研究结果表明,逆康普顿散射机制中的软光子场主要由尘埃环贡献。
综上所述,目前仍然无法确定逆康普顿散射的软光子起源,也无法确定辐射产生的位置。本文使用包含同时数据的大样本从统计角度分析逆康普顿散射机制中软光子的起源。
1 样本本文从Feimi 4-LAC活动星系核目录收集了69个有多波段准同时数据的平谱射电类星体[18],另外从文[19]收集了6个有多波段准同时数据的平谱射电类星体,共75个样本。收集的样本满足下列条件:(1) 有确定的红移;(2) 不考虑射电波段的数据,覆盖紫外到伽马射线波段,各个波段相交的观测时间小于两个月,可以构建双峰结构的光谱能量分布;(3) 有可以查到的体洛伦兹因子[20]或多普勒因子[19]。本文假设体洛伦兹因子与多普勒因子近似相等[21],使用的磁场(B)参数由文[16]中的模型拟合得到。本文的样本中有一个相对高峰值频率的源(PKS 2141+175,logνsyn=15.08 Hz)。
我们分别使用ASDC SED Builder (https://tools.ssdc.asi.it/index.jsp) 拟合来自费米样本的光谱能量分布[22],Python拟合提取自文[19]的数据构成的光谱能量分布。我们用二次函数分别拟合耀变体光谱能量分布的低能峰和高能峰,二次函数表达式为[23]
| $ {\rm{log}}(\nu {F_\nu }) = c{\left( {{\rm{log}}\nu } \right)^2} + b{\rm{log}}\nu + a, $ | (1) |
其中,a,b和c为常数。通过拟合观测数据得到的峰值频率和整个峰的积分光度都在观测者坐标系下,为了去除红移的影响,我们需要将这两个量转到活动星系核静止参考系,转换公式为
| $ {\nu _{{\rm{syn, IC}}}} = \left( {1 + z} \right)\nu _{{\rm{syn, IC}}}^{{\rm{obs}}}, $ | (2) |
| $ {(\nu {L_\nu })_{{\rm{syn, IC}}}} = 4{\rm{ \mathsf{ π} }}D_{\rm{L}}^2{(\nu {F_\nu })_{{\rm{syn, IC}}}}. $ | (3) |
其中,νsyn, ICobs为观测者坐标系下的同步峰或逆康普顿峰的峰值频率;z为红移;DL为光度距离;(νFν)syn, IC为观测者坐标系下的同步峰或逆康普顿峰的积分流量。
表 1展示了本文的75个样本,第1列为源的名称;第2列为红移;第3列为(准)同时性时间(文[19]中的数据未注明时间);第4列为取对数后的同步峰的峰值频率;第5列为取对数后的同步峰流量;第6列为取对数后的同步峰光度;第7列为取对数后的逆康普顿峰的峰值频率;第8列为取对数后的逆康普顿峰流量;第9列为取对数后的逆康普顿峰光度;第10列为磁场能量密度;第11列为体洛伦兹因子(多普勒因子以上角标a注明);第12列为观测的种子因子。
| Source name (1) |
z (2) |
Time (3) |
logνsyn/Hz (4) |
log(νFν)syn/(erg·cm-2·s-1) (5) |
log(νLν)syn/(erg·s-1) (6) |
logνIC/Hz (7) |
log(νFν)IC/(erg·cm-2·s-1) (8) |
log(νLν)IC/(erg·s-1) (9) |
UB/(erg·s-3) (10) |
Γ (11) |
SF (12) |
| PKS 0537-286 | 3.104 | 2010-03-07~12 | 12.10 | -11.471 | 47.453 | 20.472 | -9.541 | 49.383 | 0.052 18 | 12.73 | 5.599 |
| 4C +04.42 | 0.966 | 2010-06-17 | 12.41 | -10.738 | 46.943 | 21.749 | -9.860 | 47.821 | 0.053 61 | 12.11 | 4.020 |
| TXS 0653-033 | 0.634 | 2010-03-31 | 12.58 | -10.991 | 47.350 | 22.854 | -10.201 | 47.009 | 0.076 89 | 22.49 | 3.119 |
| PKS 0605-085 | 0.872 | 2010-06-07 | 12.62 | -10.914 | 46.635 | 22.989 | -10.383 | 47.167 | 0.100 23 | 14.94 | 2.904 |
| 3C 279 | 0.536 | 2010-01-15 | 12.62 | -9.764 | 48.565 | 22.141 | -9.173 | 47.861 | 0.017 43 | 12.82 | 3.694 |
| PKS 2325+093 | 1.841 | 2010-06-18~29 | 12.64 | -11.133 | 47.219 | 21.546 | -9.780 | 48.572 | 0.178 65 | 26.84 | 4.710 |
| PKS 0215+015 | 1.715 | 2010-01-29~2010-02-02 | 12.67 | -10.419 | 47.878 | 21.895 | -9.947 | 48.350 | 0.131 71 | 25.67 | 3.908 |
| PKS B1921-293 | 0.353 | 2010-09-30 | 12.73 | -9.742 | 50.088 | 21.151 | -9.764 | 46.840 | 0.039 22 | 11.33 | 4.467 |
| S5 1357+76 | 1.585 | 2010-05-24~25 | 12.73 | -11.318 | 48.842 | 22.267 | -10.556 | 47.635 | 0.086 55 | 14.34 | 3.763 |
| PKS 1244-255 | 0.635 | 2010-06-25 | 12.74 | -10.472 | 46.761 | 22.164 | -9.462 | 47.771 | 0.038 41 | 10.7 | 4.007 |
| PKS 1730-13 | 0.902 | 2010-03-14 | 12.75 | -10.218 | 47.389 | 22.946 | -9.190 | 48.418 | 0.025 01 | 13.78 | 3.261 |
| 3C 446 | 1.404 | 2010-05-22~27 | 12.75 | -10.383 | 47.678 | 21.818 | -10.028 | 48.033 | 0.048 72 | 12.00 | 4.048 |
| 3C 454.3 | 0.859 | 2009-12-04~06 | 12.76 | -9.234 | 48.299 | 22.029 | -8.210 | 49.324 | 0.191 90 | 16.95 | 4.173 |
| 3C 273 | 0.158 | 2010-06-07~23 | 12.76 | -9.478 | 46.334 | 20.247 | -8.575 | 47.239 | 0.049 30 | 20.87 | 5.947 |
| S3 0827+24 | 0.942 | 2010-04-18~19 | 12.77 | -10.595 | 47.512 | 20.788 | -11.064 | 46.569 | 0.098 86 | 13.71 | 4.668 |
| NRAO 512 | 1.66 | 2010-08-07 | 12.78 | -10.879 | 47.383 | 22.800 | -9.947 | 48.315 | 0.073 56 | 14.87 | 3.370 |
| B2 0743+25 | 2.979 | 2010-10-15 | 12.78 | -11.595 | 47.451 | 21.697 | -10.192 | 48.668 | 0.042 76 | 13.48 | 4.722 |
| TXS 0800+618 | 3.033 | 2010-04-03~04 | 12.79 | -11.479 | 47.400 | 21.626 | -10.339 | 48.539 | 0.487 90 | 15.11 | 4.691 |
| PKS 0454-234 | 1.003 | 2010-02-24~25 | 12.80 | -10.417 | 47.304 | 22.122 | -10.093 | 47.628 | 0.038 34 | 8.66 | 3.764 |
| 4C 38.41 | 1.814 | 2010-03-07 | 12.82 | -10.377 | 49.673 | 22.082 | -9.194 | 49.142 | 0.061 95 | 15.33 | 4.302 |
| 4C+47.44 | 0.735 | 2010-07-30~2010-08-01 | 12.85 | -10.764 | 47.411 | 21.808 | -10.093 | 47.274 | 0.039 71 | 9.64 | 4.280 |
| OP 313 | 0.997 | 2009-12-12~21 | 12.86 | -10.530 | 47.163 | 22.323 | -9.900 | 47.795 | 0.197 73 | 31.22 | 3.795 |
| OK 290 | 0.707 | 2010-05-07~2010-06-15 | 12.88 | -10.721 | 47.734 | 21.545 | -10.228 | 47.098 | 0.129 12 | 14.44 | 4.497 |
| B2 1324+22 | 1.4 | 2010-03-30 | 12.88 | -10.959 | 47.100 | 21.911 | -10.080 | 47.978 | 0.064 39 | 12.06 | 4.346 |
| PKS 2209+236 | 1.125 | 2009-04-15~21 | 12.92 | -10.886 | 46.937 | 23.142 | -10.488 | 47.335 | 0.011 72 | 9.30 | 2.817 |
| OJ535 | 1.418 | 2010-03-28~2010-04-08 | 12.93 | -11.219 | 46.853 | 21.506 | -10.357 | 47.715 | 0.050 34 | 12.16 | 4.793 |
| PKS 1335-127 | 0.539 | 2010-01-18~26 | 12.94 | -10.237 | 47.553 | 21.367 | -10.035 | 47.004 | 0.126 95 | 22.62 | 4.567 |
| TXS 2331+073 | 0.401 | 2009-12-20~21 | 12.94 | -10.839 | 45.895 | 21.569 | -10.425 | 46.308 | 0.347 59 | 19.93 | 4.478 |
| OI 280 | 0.889 | 210-04-01~12 | 12.95 | -10.419 | 47.152 | 21.254 | -10.270 | 47.300 | 0.051 99 | 16.18 | 4.669 |
| B3 0908+41 | 2.563 | 2010-02-25 | 12.97 | -11.400 | 47.302 | 22.629 | -10.851 | 47.853 | 0.137 43 | 18.82 | 3.464 |
| PKS 1144-379 | 1.048 | 2010-06-24 | 12.97 | -10.544 | 48.150 | 22.050 | -10.242 | 47.505 | 0.187 00 | 20.18 | 3.948 |
| S4 0917+44 | 2.19 | 2009-10-28~30 | 12.97 | -10.710 | 47.825 | 22.214 | -9.701 | 48.835 | 0.031 39 | 12.08 | 4.179 |
| OG 505 | 1.254 | 2010-04-25 | 12.98 | -10.839 | 47.103 | 22.184 | -9.870 | 48.071 | 0.028 33 | 14.77 | 4.223 |
| TXS 0404+075 | 1.133 | 2010-02-14~15 | 12.99 | -11.052 | 46.779 | 21.935 | -10.437 | 47.395 | 0.136 58 | 19.47 | 4.274 |
| PKS 1954-388 | 0.63 | 2010-04-09~14 | 13.02 | -10.456 | 50.226 | 21.636 | -9.857 | 47.348 | 0.040 35 | 14.94 | 4.621 |
| PKS 1546+027 | 0.414 | 2010-02-13~20 | 13.04 | -10.520 | 49.534 | 21.411 | -10.021 | 46.744 | 0.294 77 | 21.52 | 4.811 |
| BZQ J1514+4450 | 0.57 | 2010-04-06 | 13.05 | -11.043 | 49.257 | 22.111 | -10.559 | 46.540 | 0.032 43 | 8.30 | 4.069 |
| B2 2319+31 | 1.489 | 2009-05-20 | 13.05 | -11.434 | 46.691 | 22.734 | -10.361 | 47.764 | 0.054 23 | 22.10 | 3.771 |
| PMN J2135-5006 | 2.181 | 2010-04-22~2010-05-05 | 13.05 | -11.854 | 50.503 | 22.307 | -10.431 | 48.101 | 0.102 96 | 13.78 | 4.409 |
| PKS B1434+235 | 1.548 | 2010-06-14 | 13.06 | -11.214 | 48.980 | 22.435 | -10.684 | 47.483 | 0.096 91 | 17.16 | 3.819 |
| PKS 2345-16 | 0.576 | 2009-12-04~05 | 13.07 | -10.460 | 47.533 | 22.030 | -10.172 | 46.937 | 0.044 87 | 17.42 | 4.084 |
| PKS 0436-129 | 1.285 | 2010-07-01 | 13.07 | -11.217 | 46.750 | 22.341 | -10.590 | 47.376 | 0.045 33 | 6.30 | 3.952 |
| B3 0650+453 | 0.928 | 2010-03-22~24 | 13.13 | -10.971 | 46.645 | 22.291 | -10.079 | 47.538 | 0.119 62 | 17.76 | 4.207 |
| PKS 2255-282 | 0.926 | 2010-05-20~26 | 13.14 | -10.285 | 47.329 | 21.771 | -9.780 | 47.835 | 0.093 18 | 16.34 | 4.573 |
| PKS 0541-834 | 0.774 | 2009-11-08~11 | 13.17 | -11.438 | 45.985 | 22.193 | -10.315 | 47.106 | 0.017 01 | 11.20 | 4.464 |
| B2 2155+31 | 1.488 | 2009-07-08~12 | 13.23 | -11.160 | 46.964 | 22.462 | -10.132 | 47.992 | 0.171 09 | 10.92 | 4.222 |
| B2 1520+31 | 1.487 | - | 13.26 | -13.330 | 44.814 | 22.339 | -11.304 | 46.841 | 0.042 95 | 22.62 | 4.942 |
| 4C +28.07 | 1.213 | 2010-02-05 | 13.29 | -10.287 | 47.492 | 21.862 | -9.561 | 48.343 | 0.135 13 | 16.57 | 4.779 |
| PKS 1406-076 | 1.494 | 2010-05-23 | 13.29 | -10.796 | 47.329 | 22.239 | -10.127 | 48.001 | 0.019 78 | 10.82 | 4.319 |
| PKS 2155-83 | 1.865 | 2010-07-05~17 | 13.31 | -11.128 | 47.238 | 22.107 | -9.971 | 48.396 | 0.024 21 | 10.70 | 4.763 |
| PKS 1502+106 | 1.839 | 2010-07-29 | 13.33 | -10.721 | 49.119 | 22.810 | -9.156 | 49.195 | 0.004 08 | 25.09 | 4.290 |
| B2 1846+32A | 0.798 | 2010-10-06~19 | 13.35 | -10.695 | 49.949 | 21.509 | -9.987 | 47.466 | 0.067 63 | 12.86 | 5.116 |
| B3 1708+433 | 1.027 | 2009-12-01~02 | 13.39 | -10.971 | 49.811 | 22.131 | -9.971 | 47.756 | 0.044 88 | 11.30 | 4.682 |
| PMN 2345-1555 | 0.621 | 2010-04-01~30 | 13.40 | -10.583 | 47.390 | 22.707 | -10.029 | 47.160 | 0.331 64 | 25.46 | 3.892 |
| PMN J1959-4246 | 2.178 | 2010-04-05~14 | 13.41 | -11.076 | 50.365 | 22.173 | -10.082 | 48.447 | 0.121 92 | 17.16 | 4.674 |
| PKS 0420-01 | 0.916 | 2009-08-27 | 13.41 | -9.762 | 47.840 | 22.218 | -9.625 | 47.978 | 0.059 68 | 12.43 | 4.209 |
| PKS 1203-26 | 0.789 | 2010-11-01~2010-12-31 | 13.43 | -10.932 | 48.288 | 21.246 | -10.346 | 47.097 | 0.045 21 | 12.40 | 5.437 |
| PKS 0906+01 | 1.024 | 2010-04-18~2010-05-05 | 13.44 | -10.556 | 47.167 | 21.426 | -9.535 | 48.187 | 0.193 62 | 15.32 | 5.503 |
| PKS 1510-089 | 0.36 | - | 13.45 | -12.256 | 44.388 | 22.138 | -11.077 | 45.567 | 0.078 64 | 12.08 | 4.884 |
| MG2 J110606+2812 | 0.843 | 2010-02-07~2010-03-07 | 13.46 | -10.842 | 48.011 | 21.994 | -10.358 | 47.156 | 0.059 02 | 17.42 | 4.652 |
| 4C+29.45 | 0.724 | 2010-05-28~2010-06-11 | 13.49 | -10.337 | 47.014 | 22.319 | -9.721 | 47.630 | 0.052 31 | 25.90 | 4.433 |
| MG2 J071354+1934 | 0.54 | 2009-12-15~17 | 13.51 | -10.613 | 47.472 | 22.323 | -10.061 | 46.980 | 0.153 08 | 15.76 | 4.400 |
| PMN J2145-3357 | 1.361 | 2009-09-22~24 | 13.52 | -10.991 | 50.642 | 23.086 | -10.378 | 47.650 | 0.000 67 | 14.43 | 3.641 |
| PKS 0601-70 | 2.409 | 2008-12-01~30 | 13.58 | -10.924 | 47.714 | 22.717 | -10.143 | 48.494 | 0.001 29 | 33.06a | 4.195 |
| OC 457 | 0.859 | - | 13.60 | -11.726 | 45.829 | 22.652 | -11.588 | 45.967 | 0.000 32 | 21.45a | 3.916 |
| PKS B1035-281 | 1.066 | 2010-01-22~23 | 13.62 | -11.118 | 47.873 | 21.974 | -10.287 | 47.478 | 0.003 12 | 20.63 | 5.047 |
| PKS 0347-211 | 2.944 | - | 13.66 | -12.267 | 46.602 | 22.296 | -11.358 | 47.511 | 0.000 25 | 25.82 | 4.813 |
| CRATES J1208+5441 | 1.344 | 2010-05-16~21 | 13.71 | -11.183 | 48.427 | 21.819 | -10.014 | 48.001 | 0.000 32 | 8.80 | 5.465 |
| PMN J1347-3750 | 1.3 | 2010-09-20 | 13.77 | -11.123 | 48.703 | 21.840 | -10.236 | 47.743 | 0.004 31 | 24.00 | 5.337 |
| MG2 J153938+2744 | 2.191 | 2010-03-17 | 13.77 | -11.383 | 49.396 | 23.871 | -10.695 | 47.841 | 0.000 25 | 12.11 | 3.114 |
| CLASS J1333+5057 | 1.362 | 2010-03-12~17 | 13.79 | -11.699 | 47.370 | 22.375 | -10.526 | 47.502 | 0.000 53 | 23.00 | 4.974 |
| 4C+55.17 | 0.896 | 2009-10-31~2009-11-02 | 13.82 | -10.658 | 47.431 | 24.289 | -9.682 | 47.897 | 0.001 75 | 14.94 | 2.945 |
| GB6 J0654+5042 | 1.253 | 2010-01-15 | 14.01 | -10.910 | 47.030 | 23.221 | -10.354 | 47.586 | 0.001 41 | 14.77 | 3.965 |
| PKS 1454-354 | 1.424 | - | 14.11 | -12.441 | 45.656 | 22.441 | -11.153 | 46.945 | 0.002 99 | 16.00 | 5.290 |
| PKS 2141+175 | 0.213 | - | 15.08 | -11.710 | 44.412 | 23.918 | -11.580 | 44.542 | 0.003 08 | 10.00 | 4.114 |
文[24]使用均匀的单区轻子模型进行分析,假设电子是以截断幂律谱的形式注入相对论性运动的等离子体团,注入电子随着时间演化,多波段的辐射全部来自这个以相对论性速度运动的致密辐射区。研究发现,如果逆康普顿散射过程由外康普顿过程主导,则外康普顿过程贡献的流量和同步峰流量的关系近似为[24]
| $ \frac{{{U_{\rm{B}}}{{(\nu {F_\nu })}_{{\rm{EC}}}}}}{{{U_{{\rm{ext}}}}{{(\nu {F_\nu })}_{{\rm{syn}}}}}} \approx {\delta ^{1 + \alpha }}, $ | (4) |
其中,UB=B2/8π为磁场能量密度,B为磁场;Uext为外部光子的能量密度;δ为多普勒因子;α为光子谱指数。假设Uext恒定[17],常数通常会离散数据,并不影响相关性的分析。因此,(4) 式可以预测逆康普顿峰流量与同步峰流量的比值和多普勒因子之间的相关性。如果逆康普顿散射过程由同步辐射自康普顿过程主导,那么同步辐射自康普顿过程产生辐射的流量和同步辐射的流量之比为[24]
| $ \frac{{{(\nu {{F}_{\nu }})}_{\text{SSC}}}}{{{(\nu {{F}_{\nu }})}_{\text{syn}}}}\approx \frac{2}{3}({{\sigma }_{\text{T}}}{{n}_{\text{eo}}}{{r}_{\text{b}}}){{\left( \frac{{{{\boldsymbol{\epsilon}} }_{\text{s}}}}{{{{\boldsymbol{\epsilon}} }_{\text{C}}}} \right)}^{\alpha -1}}\text{ln}{{\overline \sum}_{\text{C}}}{{{\boldsymbol{\epsilon}} }_{\text{C}}}\propto {{n}_{\text{eo}}}, $ | (5) |
其中,σT为汤姆逊散射截面;neo为非热辐射电子数密度的归一化因子;rb为辐射区半径;
图 1展示了整个样本log[UB(νFν)EC/Uext(νFν)syn] 与logδ的相关性。斯皮尔曼测试显示置信水平p=0.000 3 (在5%水平下显著),相关系数R=0.473 0。我们用最小二乘法做线性回归得到的结果为log[UB(νFν)EC/Uext(νFν)syn]=(2.40±0.36)logδ+(-4.76±0.43)。上述结果表明,平谱射电类星体中逆康普顿散射机制主要由外康普顿过程主导。
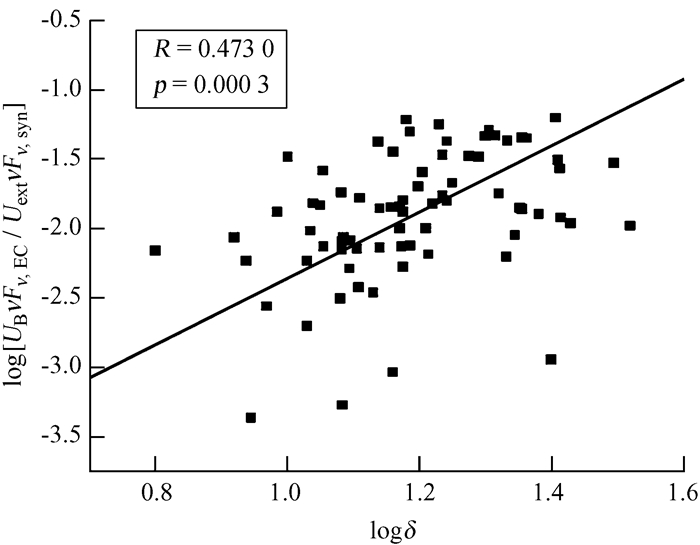
|
| 图 1 整个样本log[UB(νFν)EC/Uext(νFν)syn]与logδ的相关性分析。实线表示最佳拟合 Fig. 1 The correlation for the whole sample between log[UB(νFν)EC/Uext(νFν)syn] and logδ. The solid line is the best linear fitting |
根据文[25]的结论,同步峰的峰值频率可能跟粒子能被加速到达的最大能量有关。对于目前更为常见的低/中/高同步峰频分类法[26],统计上平谱射电类星体大部分属于低同步峰频,并且同步峰的峰值频率集中在logνsyn≈13.3 Hz,还有逆康普顿散射发生在汤姆逊区域(The Thomson regime)。所以本文要确定样本中不同峰频的平谱射电类星体是否也有一些物理上的不同,按照同步峰的峰值频率集中在约13.3 Hz把样本分成两个子样本,即相对低同步峰的峰频种群(12.10 Hz < logνsyn < 13.05 Hz,包含38个源,称为低峰频种群) 与相对高同步峰的峰频种群(13.05 Hz < logνsyn < 14.11 Hz,包含37个源,称为高峰频种群)。图 2分别展示了两个种群log[UB(νFν)EC/Uext(νFν)syn]与logδ的相关性。低峰频种群的斯皮尔曼测试显示置信水平p=0.013 3,相关系数R=0.520,我们用最小二乘法做线性回归得到的结果为log[UB(νFν)EC/Uext(νFν)syn] =(2.13 ± 0.45)logδ +(-4.48 ± 0.55)。高峰频种群的斯皮尔曼测试显示置信水平p=0.008 8,相关系数R=0.433,我们用最小二乘法做线性回归得到的结果为log[UB(νFν)EC/Uext(νFν)syn] =(2.72 ± 0.58)logδ +(-5.09 ± 0.69)。上述分析结果表明,分成两个子样本进行研究得到的结果与整个样本的结果没有明显差异,在平谱射电类星体样本中,逆康普顿散射机制主要由外康普顿过程主导。
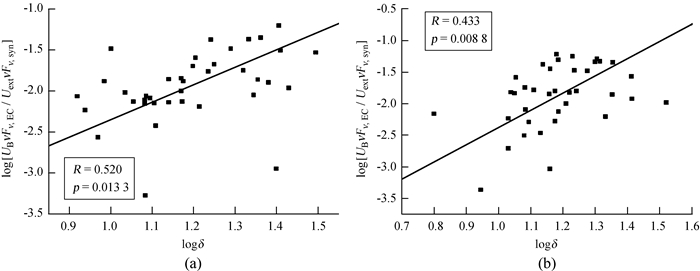
|
| 图 2 两个种群log[UB(νFν)EC/Uext(νFν)syn]与logδ的相关性分析。(a) 低峰频种群(12.10 Hz < logνsyn < 13.05 Hz) 包含38个源;(b) 高峰频种群(13.05 Hz < logνsyn < 14.11 Hz) 包含37个源。实线表示最佳拟合 Fig. 2 The correlation for two populations between log[UB(νFν)EC/Uext(νFν)syn] and logδ. (a) the low frequency peak populations (12.10 Hz < logνsyn < 13.05 Hz) containing 38 sources; (b) the high frequency peak populations (13.05 Hz < logνsyn < 14.11 Hz) containing of 37 sources. The solid line is the best linear fitting |
上一节的研究发现,平谱射电类星体的逆康普顿散射机制由外康普顿过程主导,在外康普顿过程中存在多种软光子起源,例如吸积盘、宽线区和尘埃环等。为了进一步调查软光子的来源,我们使用文[17]提出的自举法计算低、高峰频种群观测的种子因子分布(Seed Factor Distribution)(数值见表 1)。计算种子因子的表达式为[17]
| $ SF=\text{log}10\frac{U_{\text{ext}}^{1/2}}{{{{\boldsymbol{\epsilon}} }_{0}}}=\text{log}10\left( 3.22\times {{10}^{4}} \right)\frac{C{{D}^{1/2}}{{\nu }_{\text{syn, 13}}}}{{{\nu }_{\text{IC, 22}}}}\text{Gauss}, $ | (6) |
其中,Uext为喷流外部光子能量密度(在厘米-克-秒(CGS)单位制下);
我们使用双侧柯尔莫戈洛夫检验(two-sided Kolmogorov-Smirnov test) 对各个样本的种子因子分布进行正态检验后发现,在低、高峰频种群中均不能拒绝正态性假设。在低峰频种群中,拒绝正态性假设的显著性为0.37σ (p=0.71);在高峰频种群中,拒绝正态性假设的显著性为0.01σ (p=0.99),均小于2σ的置信水平。因此,这些样本的种子因子服从正态分布,与文[17]的结果一致。
基于自举法,我们用低、高峰频种群中观测的种子因子分布构建了观测种子因子的大样本(低峰频种群3.8 × 105个,高峰频种群3.7 × 105个),从大样本中构建104个包含相同源数目的替代样本,使用替代样本分别估算不同种群中观测的种子因子分布的中位数(Obsmedian) 及2σ置信区间,即
| $ {\rm{低峰频种群}}, Ob{s_{{\rm{median}}}} = 4.20_{ - 0.19}^{ + 0.21}, $ | (7) |
| $ 高峰频种群, Ob{s_{{\rm{median}}}} = 4.43_{ - 0.21}^{ + 0.24}. $ | (8) |
图 3展示了两个种群的种子因子分布直方图,并且标注了理论上期望的宽线区种子因子和尘埃环种子因子分布。从图 3可以发现,直方图峰值靠近尘埃环的位置。
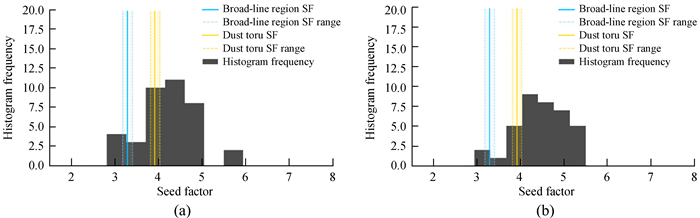
|
| 图 3 两个种群的种子因子分布直方图。(a) 低峰频种群(12.10 Hz < logνsyn < 13.05 Hz) 包含38个源的种子因子;(b) 高峰频种群(13.05 Hz < logνsyn < 14.11 Hz) 包含37个源的种子因子。直方图用黑色区域展示;蓝色实线和虚线分别表示理论上的宽线区种子因子及范围;黄色实线和虚线分别表示理论上尘埃环的种子因子及范围。直方图的区间由matplotlib.pyplot.hist自动选择。从两幅图中可以发现直方图的峰值靠近尘埃环的位置 Fig. 3 Histogram of two populations observed seed factor. (a) The low frequency peak populations (12.10 Hz < logνsyn < 13.05 Hz) containing the seed factor of 38 sources; (b) the high frequency peak populations (13.05 Hz < logνsyn < 14.11 Hz) containing the seed factor of 37 sources. The histogram is plotted in black; the expected broad-line region seed factor and range are shown in blue, with solid and dashed lines, respectively; the expected dust torus seed factor and range are shown in yellow, with solid and dashed lines, respectively. The histogram was binned using the auto option for the matplotlib.pyplot.hist. As can be seen from this histogram, the seed factor distribution peaks close to the seed factor distribution of dust torus |
种子因子分布的直方图没有包含估计的不确定性。为了包含估计的不确定性,我们基于自举法实现了低、高峰频种群的核密度估计(Kernel Density Estimation, KDE),并运用文[27]的方法对核密度估计中的带宽自动进行平滑处理[17]。图 4展示了两个种群的核密度估计,在图 4中,(a) 为低峰频种群,观测的种子因子分布与尘埃环的分布相交,表明软光子很可能由尘埃环主导;(b) 为高峰频种群,观测的种子因子分布与理论上的种子因子分布不相交,表明软光子可能不是由宽线区或尘埃环单一主导。
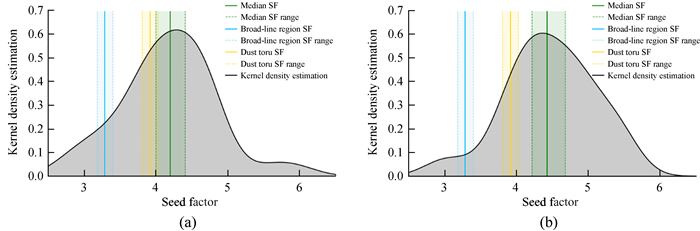
|
| 图 4 两个种群的核密度估计。(a) 低峰频种群(12.10 Hz < logνsyn < 13.05 Hz) 包含38个源的种子因子;(b) 高峰频种群(13.05 Hz < logνsyn < 14.11 Hz) 包含37个源的种子因子。黑色实线是核密度估计曲线;灰色区域是为了视觉辅助;蓝色实线和虚线分别表示期望的宽线区种子因子及范围;黄色实线和虚线分别表示期望的尘埃环种子因子及范围;绿色实线和虚线分别表示观测的种子因子中位数及2σ置信区间。外观上,核密度估计近似正态分布。在2σ的置信水平下,双侧柯尔莫戈洛夫检验显示均不能拒绝正态性假设,从左到右拒绝正态性假设的显著性分别为0.37σ (p=0.71)和0.01σ(p=0.99) Fig. 4 Kernel density estimate of two populations. (a) The low frequency peak populations (12.10 Hz < logνsyn < 13.05 Hz) containing the seed factor of 38 sources; (b)the high frequency peak populations (13.05 Hz < logνsyn < 14.11 Hz) containing the seed factor of 37 sources. The black solid line is the kernel density estimation; the gray area is the visual aid; the expected broad-line region seed factor and range are shown in blue, with solid and dashed lines, respectively; the expected dust torus seed factor and range are shown in yellow, with solid and dashed lines, respectively; the median of observed seed factor and 2σ confidence interval are shown in green, with solid and dashed lines, respectively. The KDE has the general appearance of a normal distribution. A two-sided Kolmogorov-Smirnov test indicates that normality cannot be rejected significantly (using a rejection significance threshold of 2σ), with rejection significance of 0.37σ(p=0.71) and 0.01σ (p=0.99) from left to right, respectively |
为了进一步检验观测的种子因子分布与宽线区还是尘埃环的位置对应,我们分别计算了低、高峰频种群中观测种子因子分布与理论上期望的种子因子分布之间拒绝中位数相等的显著性。在标准差方面,对于低峰频种群,拒绝的显著性为
| $ \sigma (Ob{s_{{\rm{median}}}} - BL{R_{{\rm{median}}}}) = 8.28\sigma , $ | (9) |
| $ \sigma (Ob{s_{{\rm{median}}}} - D{T_{{\rm{median}}}}) = 2.55\sigma ; $ | (10) |
在高峰频种群,拒绝的显著性为
| $ \sigma (Ob{s_{{\rm{median}}}} - BL{R_{{\rm{median}}}}) = 10.39\sigma , $ | (11) |
| $ \sigma (Ob{s_{{\rm{median}}}} - D{T_{{\rm{median}}}}) = 4.66\sigma . $ | (12) |
因此,低峰频中观测的种子因子分布与理论上期望的尘埃环种子因子分布的拒绝显著性最小,表明低峰频种群中软光子的起源很可能由尘埃环主导。高峰频种群中虽然观测种子因子分布与尘埃环种子因子分布的显著性比宽线区种子因子分布的拒绝显著性小,但是核密度估计显示出明显的差异,表明软光子的起源对于尘埃环或许不是单一的位置,软光子可能有宽线区和尘埃环的贡献。
3 讨论与总结研究发现, 无论是整个样本还是按数量均分的两个子样本,在log[UB(νFν)EC/UBLR(νFν)syn]和logδ的相关性方面,图 1与图 2没有明显的差异,这表明轻子模型框架下,平谱射电类星体中的逆康普顿散射机制很可能由外康普顿过程主导。图 1中包含75个平谱射电类星体,而图 2 (a),(b)分别包含38个和37个平谱射电类星体,图上的数据分布两者均存在一定的弥散,这从某种程度上削弱本文的结论。随着越来越多观测设备投入使用,未来可以收集到更多的样本,进一步验证轻子模型框架下高能辐射的主导过程。
种子因子的计算基于多波段光谱能量分布的拟合,要求宽带辐射没有明显的光变现象[17]。我们使用文[17]的方法计算样本的种子因子。图 3的直方图展示了观测的种子因子分布,该直方图没有包含估计的不确定性,图 4的核密度估计包含了估计的不确定性。从图 3可以发现,观测的种子因子分布集中在峰频位置,而图 4的核密度估计曲线展示了相同的结果,并且展示了由样本计算得到观测的种子因子分布与文[17]理论上期望的种子因子分布之间的差异。从图 4 (a)可以发现,观测的种子因子分布在统计上与尘埃环种子因子分布的范围相交,表明在低峰频的种群中软光子很可能由尘埃环主导。从图 4 (b)可以发现,观测的种子因子分布超过了理论上期望的宽线区和尘埃环种子因子分布的范围,表明在高峰频种群中尘埃环很可能不是主导软光子的单一位置,可能有宽线区和尘埃环共同的贡献。文[17]的研究发现,平谱射电类星体的辐射区与尘埃环的位置在统计上一致,表明软光子主要是尘埃环的贡献。与文[17]的研究结果相比,本文的样本在不同种群中显示了不同的结果。图 3的直方图分别包含38个和37个源的种子因子,因此统计上计算的种子因子偏少,希望未来进一步增加同时性样本,并且使用不同方法获得的观测量做进一步分析验证。
本文从统计上研究了75个平谱射电类星体中软光子的起源。相关性分析结果表明,平谱射电类星体的逆康普顿散射机制很可能由外康普顿过程主导。种子因子分布进一步检验了外康普顿过程中软光子的来源,结果表明不同的种群在统计上有不同的结果。
致谢: 感谢Harvey博士在种子因子方面的帮助。
| [1] | URRY C M, PADOVANI P. Unified schemes for radio-loud active galactic nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107(715): 803–845. |
| [2] | BLANDFORDR D, REES M J. Extended and compact extragalactic radio sources: interpretation and theory[J]. Physica Scripta, 1978, 17(3): 265–274. DOI: 10.1088/0031-8949/17/3/020 |
| [3] | BÖTTCHER M. Modeling the emission processes in blazars[J]. Astrophysics and Space Science, 2007, 1: 95–104. |
| [4] | BLOOM S D, MARSCHER A P. An analysis of the synchrotron self-compton model for the multi-wave band spectra of blazars[J]. The Astrophysical Journal, 1996, 461: 657–663. DOI: 10.1086/177092 |
| [5] | DERMER C D, SCHLICKEISER R. Model for the high-energy emission from blazars[J]. The Astrophysical Journal, 1993, 416(2): 458–484. |
| [6] | SIKORA M, BEGELMAN M C, REES M J. Comptonization of diffuse ambient radiation by a relativistic jet: the source of gamma rays from blazars?[J]. The Astrophysical Journal, 1994, 421: 153–162. DOI: 10.1086/173633 |
| [7] | CASTIGNANI G, DE ZOTTI G, et al. AGN torus emission for a homogeneous sample of bright flat-spectrum radio quasars[J]. Astronomy & Astrophysics, 2015, 573: A125. |
| [8] | PATINO-ALVAREZ V M, FERNANDES S, CHAVUSHYAN V, et al. Multiwavelength photometric and spectropolarimetric analysis of the FSRQ 3C 279[J]. Monthly Notices of the Royal Astronomical Society, 2018, 479(2): 2037–2064. DOI: 10.1093/mnras/sty1497 |
| [9] | TAVECCHIO F, GHISELLINI G, BONNOLI G, et al. Constraining the location of the emitting region in Fermi blazars through rapid γ-ray variability[J]. Monthly Notices of the Royal Astronomical Society, 2010, 405(1): L94–L98. DOI: 10.1111/j.1745-3933.2010.00867.x |
| [10] | RAMAKRISHNAN V, HOVATTA T, NIEPPOLA E, et al. Locating the γ-ray emission site in Fermi/LAT blazars from correlation analysis between 37 GHz radio and γ-ray light curves[J]. Monthly Notices of the Royal Astronomical Society, 2015, 452(2): 1280–1294. DOI: 10.1093/mnras/stv321 |
| [11] | ALBERT J, ALIU E, ANDERHUB H, et al. Very-high-energy gamma rays from a distant quasar: how transparent is the universe?[J]. Science, 2008, 320(5884): 1752–1754. DOI: 10.1126/science.1157087 |
| [12] | TAVECCHIO F, GHISELLINI G, BONNOLI G, et al. Constraining the location of the emitting region in Fermi blazars through rapid γ-ray variability[J]. Monthly Notices of the Royal Astronomical Society, 2010, 405(1): L94–L98. DOI: 10.1111/j.1745-3933.2010.00867.x |
| [13] | ALEKSIC J, ANTONELLI L A, ANTORANZ P, et al. MAGIC discovery of very high energy emission from the FSRQ PKS 1222+21[J]. The Astrophysical Journal Letters, 2011, 730(1): L8. DOI: 10.1088/2041-8205/730/1/L8 |
| [14] |
张浩, 张娟, 刘磊, 等. 空间VLBI数据记录格式RDF解析与数据解码[J]. 天文研究与技术, 2020, 17(2): 163–170 ZHANG H, ZHANG J, LIU L, et al. A study of space VLBI data recording format-RDF and its data decoding[J]. Astronomical Research & Technology, 2020, 17(2): 163–170. |
| [15] | MARSCHER A P, JORSTAD S G, LARIONOV V M, et al. Probing the inner jet of the quasar PKS 1510-089 with multi-waveband monitoring during strong gamma-ray activity[J]. The Astrophysical Journal Letters, 2010, 710(2): L126. DOI: 10.1088/2041-8205/710/2/L126 |
| [16] | TAN C, XUE R, DU L M, et al. The physical properties of Fermi-4LAC flat spectrum radio quasars[J]. The Astrophysical Journal Supplement Series, 2020, 248(2): 27. DOI: 10.3847/1538-4365/ab8cc6 |
| [17] | HARVEY A L W, GEORGANOPOULOS M, MEYER E T. Powerful extragalactic jets dissipate their kinetic energy far from the central black hole[J]. Nature Communications, 2020, 11(1): 1–5. DOI: 10.1038/s41467-019-13993-7 |
| [18] | ABDOLLAHI S, ACERO F, ACKERMANN M, et al. Fermi large area telescope fourth source catalog[J]. The Astrophysical Journal Supplement Series, 2020, 247(1): 33. DOI: 10.3847/1538-4365/ab6bcb |
| [19] | HU W, DAI B Z, ZENG W, et al. The properties of jet in luminous blazars under the equipartition condition[J]. New Astronomy, 2017, 52: 82–95. DOI: 10.1016/j.newast.2016.10.011 |
| [20] | XIONG D R, ZHANG X. The connections between bulk Lorentz factor, black hole mass and accretion in Fermi FSRQs[J]. Astrophysics and Space Science, 2014, 352(2): 809–818. DOI: 10.1007/s10509-014-1967-y |
| [21] | MARASCHI L, TAVECCHIO F. The jet-disk connection and blazar unification[J]. The Astrophysical Journal, 2003, 593(2): 667–675. DOI: 10.1086/342118 |
| [22] | STRATTA G, CAPALBI M, GIOMMI P, et al. The ASDC SED Builder tool description and tutorial[EB/OL]. (2011-03-03)[2021-01-18]. https://arxiv.org/pdf/1103.0749.pdf. |
| [23] |
彭瑞, 谢照华, 薛瑞, 等. 费米耀变体峰值参量、康普顿主导、谱指数之间相关性的研究[J]. 天文研究与技术, 2019, 16(4): 401–409 PENG R, XIE Z H, XUE R, et al. The peak information, the Compton dominance, the spectral index diagram, and the correlations for Fermi blazars[J]. Astronomical Research & Technology, 2019, 16(4): 401–409. |
| [24] | DERMER C D, STURNER S J, SCHLICKEISER R. Nonthermal Compton and synchrotron processes in the jets of active galactic nuclei[J]. The Astrophysical Journal Supplement Series, 1997, 109(1): 103. DOI: 10.1086/312972 |
| [25] | PADOVANI P, GIOMMI P. The connection between x-ray-and radio-selected BL Lacertae objects[J]. The Astrophysical Journal, 1995, 444: 567–581. DOI: 10.1086/175631 |
| [26] | ABDO A A, ACKERMANN M, AGUDO I, et al. The spectral energy distribution of Fermi bright blazars[J]. The Astrophysical Journal, 2010, 716(1): 30–70. DOI: 10.1088/0004-637X/716/1/30 |
| [27] | SILVERMAN B W. Density estimation for statistics and data analysis[M]. Boca Raton: CRC Press, 1986. |



