2. 武汉地震计量检定与测量工程研究院有限公司, 湖北 武汉 430000
2. Wuhan Seismic Metrological Verification&Surveying Engineering Institute Corporation, LTD, Wuhan 430000, China
随着精密工程测量学、地球动力学、气象学等领域对全球定位系统数据处理精度要求的提高,静态定位数据处理方法研究逐步深入。文[1]基于快速星历研究基线解算精度,得出不同长度的基线在固定轨道模式和松弛轨道模式下精度有所不同;文[2]研究了气象数据对基线解算精度和降水量估计值的影响;文[3]实验研究了小区域全球定位系统网GAMIT解算结果与国际全球定位系统服务(International GPS Service, IGS)站选取的关系;文[4]讨论了陆态网测站分区的方案;文[5]基于GAMIT软件研究了不同对流层延迟参数估计时间间隔长短对不同长度基线解算的影响。以上研究表明,不同的参数设置对全球定位系统数据解算精度有一定影响[6],因此,研究不同的数据处理策略在解算高精度全球定位系统定位中具有重要意义。
上述文献研究全球定位系统数据处理时,多采用基线成果的均方根(Root Mean Square, RMS)作为精度指标进行评价,该指标在一定程度上能够反应基线成果的精度,然而基线的均方根是一个内符合精度指标。均方根与成果质量有一定关系,成果质量不好时,均方根较大,但反过来却不一定成立。鉴于大多数文献未对数据处理的外部可靠性进行分析或分析较少,本文在全球定位系统数据处理时兼顾成果的内外精度,分别研究了海潮模型、轨道模式设置、星历产品等因素对基线解算精度的影响,并采用基线均方根、坐标分量偏差等作为精度评定指标。在上述实验基础上,基于误差理论提出对同一组观测数据基线进行多次解算,进而将多次基线组合平差的方法,设计专门实验验证该方法对提高全球定位系统数据处理质量的有效性。
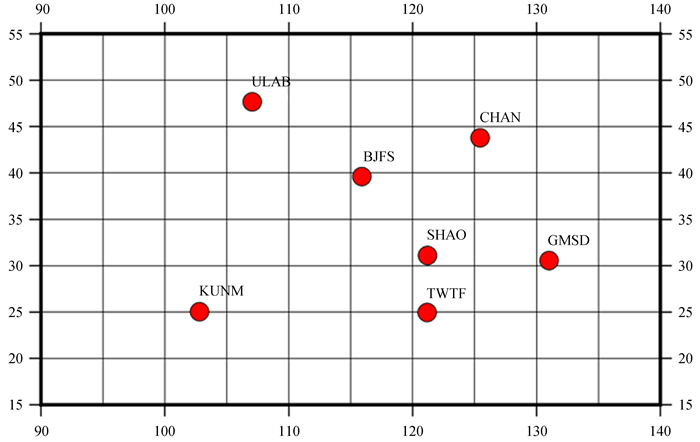
1 数据处理策略及精度分析文中选用全球分布的国际全球定位系统服务跟踪站的ULAB,CHAN,GMSD,TWTF,KUMN,BJFS和SHAO共7个站点数据为基础,计算数据的点位分布如图 1。计算数据资料为2013年01月01日单日数据,借助高精度全球定位系统数据处理软件GAMIT10.71进行基线解算,在各项指标合格的基础上进行平差计算。因国际全球定位系统服务站点坐标精度极高(在2 mm以内),因此可以看作真值[7],平差成果直接和国际全球定位系统服务站公布的成果进行比较,并结合基线解算的均方根评定精度。为防止计算成果因已知点位网型对成果解算产生不利影响,后续实验均选择CHAN,TWTF,GMSD,ULAB及KUMN为已知点,BJFS和SHAO为待定点进行对比验证。
|
| 图 1 国际全球定位系统服务站点位分布图 Fig. 1 Location map of IGS stations |
海洋受日月等天体引力的影响,海洋潮汐引起的地表周期性负荷形变在沿海地区垂直方向最大可达分米量级[8],对水平方向也有不同程度的影响[9]。目前,国际上的主要海潮模型有十多种,本文选用FES2004,NAO99b,CSR4.0及GOT00海潮模型进行实验。实验选用的海潮模型涵盖范围、分辨率及获取方法如表 1[10-13]。
| Model | Coverage area | Methods | Resolutio/(°) | Method of data acquisition |
| FES2004 | global | Blending assimilation | 0.125 × 0.125 | T/P + ERS1/2 Tide gauge station + hydrodynamic model |
| NAO99b | global | Representer ssimilation | 0.5 × 0.5 | T/P + hydrodynamic model |
| CSR4.0 | 66S°~66N° | Response and empirical method | 0.5 × 0.5 | T/P Inversion |
| GOT00 | global | Assimilation | 0.5 × 0.5 | T/P + RES-2 |
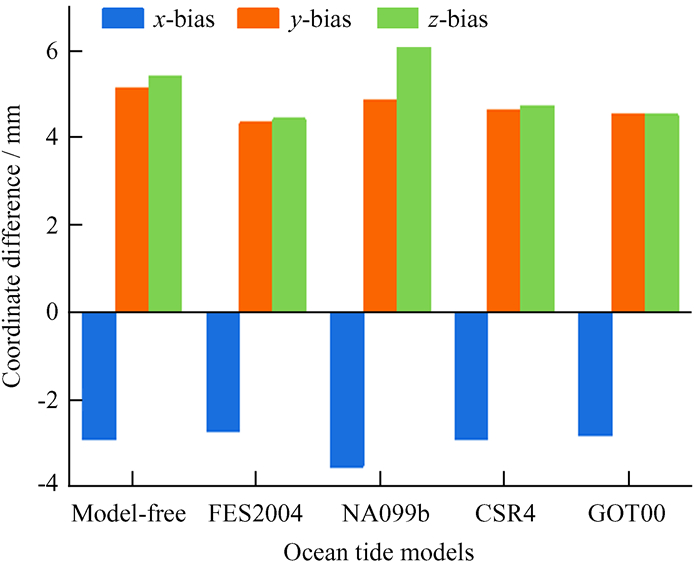
为分析海潮模型对解算成果的影响,我们设计了以下5种方案进行数据处理实验: (1)不加海潮模型改正;(2)加入FES2004海潮模型改正;(3)加入NAO99b海潮模型改正;(4)加入CSR4.0海潮模型改正;(5)加入GOT00海潮模型改正。实验参数设置为卫星截止高度角15°,已知站点约束为0.050 m,待定点50 m,观测值选项设定为LC_HELP,轨道模式选用固定(BASELINE)模式,GAMIT10.71软件参数设置项除了海潮模型,其它设置完全相同,实验结果列于表 2。为更直观地体现模型解算结果的影响,将解算的BJFS和SHAO两国际全球定位系统服务站的坐标分量的偏差分别绘制于图 2和图 3。
| Types | Baseline (RMS) | Station | x-bias | y-bias | z-bias |
| Model-Free | 0.212 60 | BJFS | -2.9 | 5.1 | 5.4 |
| SHAO | -8.3 | 3.6 | -2.8 | ||
| FES2004 | 0.187 83 | BJFS | -2.7 | 4.3 | 4.4 |
| SHAO | -7.4 | 1.5 | -4.4 | ||
| NAO99b | 0.194 18 | BJFS | -3.5 | 4.8 | 6.0 |
| SHAO | -7.1 | 1.4 | -3.0 | ||
| CSR4.0 | 0.207 38 | BJFS | -2.9 | 4.6 | 4.7 |
| SHAO | -7.7 | 1.7 | -4.2 | ||
| GOT00 | 0.212 44 | BJFS | -2.8 | 4.5 | 4.5 |
| SHAO | -7.6 | 1.9 | -4.2 |
|
| 图 2 海潮模型对BJFS站计算成果的影响 Fig. 2 The effect of ocean tide loading model on the calculation results of BJFS station |
|
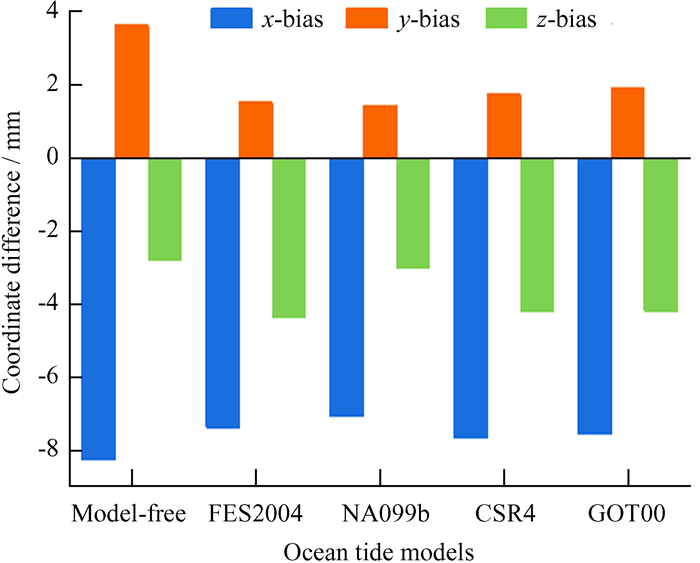
| 图 3 海潮模型对SHAO站计算成果的影响 Fig. 3 The effect of ocean tide loading model on the calculation results of SHAO station |
由表 2可知,加入FES2004海潮模型解算的基线均方根最低,NAO99b其次,其它模型较未加海潮模型的基线均方根稍优。实验结果显示,加入海潮模型后,整网基线解算获得的内符合精度均比未加入海潮模型的成果更优。
由图 2、图 3可知,将海潮模型加入基线解算后,BJFS站x, y和z方向偏差与无模型解算结果对比占优,对SHAO站的y方向精度提升明显,对x方向精度也有一定程度的提升,z方向偏差则稍有增加。FES2004海潮模型对BJFS站x, y和z任意方向的精度提升都是最优,对SHAO站提升不如NAO99b模型,基本与其它模型相当。NAO99b模型对SHAO站精度的提升最优,对BJFS站精度的提升表现较差,主要原因是BJFS站在内陆地区,受海潮影响较小,而SHAO站距东海较近,受海潮影响较大。一方面是海潮模型依据一定时期内的观测数据建模而成,模型本身有一定的误差;另一方面,每日的海潮是不确定的,由模型计算具体年积日时也有一定的误差。
综合基线均方根及坐标偏差两项指标,上述几种方案中,加入FES2004海潮模型改正的成果内外符合度最佳,又因其模型分辨率高,在一般点位测量时,内插模型数据精度理论上比其它模型高,因此,在利用海潮模型解算成果时应优先考虑FES2004海潮模型。
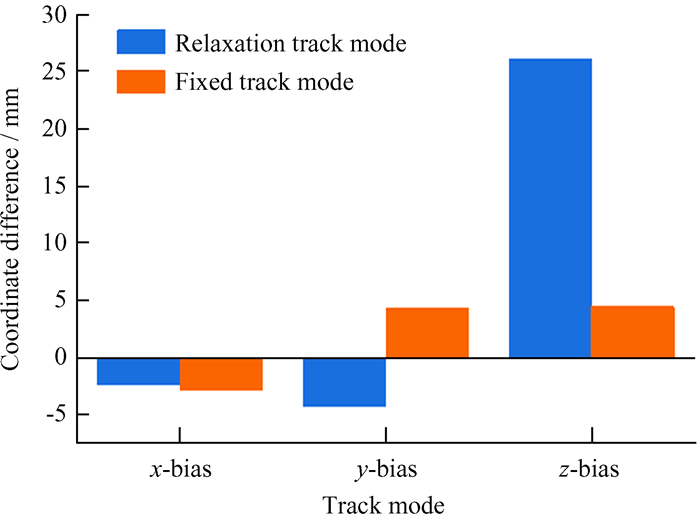
1.2 轨道模式设置的影响目前,常用的基线解算模式有3种,为分析长距离基线解算模式及成果的可靠性,分别设置轨道固定和轨道松弛两种解算模式进行实验。实验参数设置同前文,仅轨道模式分别选择轨道固定和轨道松弛两种模式,其约束采用软件默认值。限于篇幅,文中仅列出了前文验证的FES2004作为海潮模型参数,其它设置完全相同。基线解算及网平差成果统计见表 3。为更直观地比较两种轨道模式设置对解算成果的影响,图 4、图 5给出了BJFS和SHAO两种模式设置获得的坐标分量与国际全球定位系统服务站公布的坐标分量的偏差对比图。
| Types | RMS | Maximum relative error | Station | x-bias | y-bias | z-bias |
| Orbital fixing | 0.144 98 | SHAO~TWTF | BJFS | -2.3 | -4.3 | 26.1 |
| 1/127487000 | SHAO | -13.9 | -3.5 | 19.7 | ||
| Orbital relaxation | 0.176 24 | SHAO~TWTF | BJFS | -2.7 | 4.3 | 4.4 |
| 1/86509000 | SHAO | -7.4 | 1.5 | -4.4 |
|
| 图 4 轨道模式设置对BJFS站成果的影响 Fig. 4 The effect of setting of track mode on the achievements of BJFS station |
|
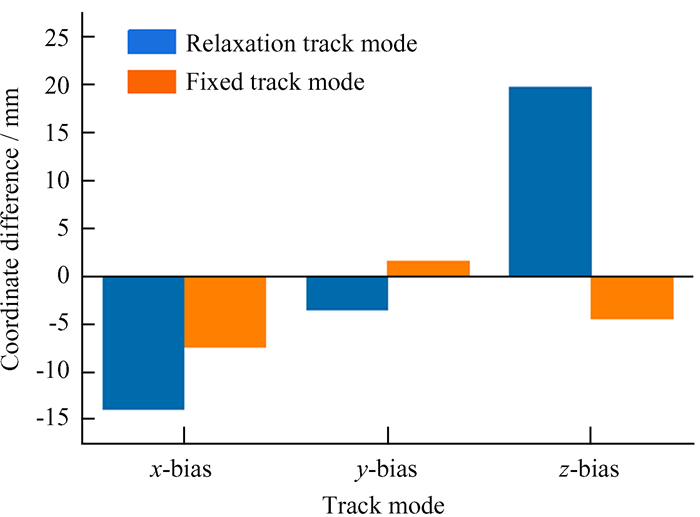
| 图 5 轨道模式设置对SHAO站成果的影响 Fig. 5 The effect of setting of track mode on the achievements of SHAO station |
由表 3可知,轨道松弛模式比轨道固定模式解算的基线均方根小,且全网最弱边相对中误差轨道松弛模式计算结果更优,说明此模式解算的基线内符合精度较高,主要原因是轨道松弛模式解算时,把星历误差同时作为未知数进行求解,相当于在基线网平差前把基线进行一次误差调整,因而内符合精度表现良好;而轨道固定模式相当于忽略了星历误差,虽然解算的基线均方根较轨道松弛解的精度稍差,但其坐标成果对比国际全球定位系统服务站公布的坐标偏差较小,说明轨道固定模式的外符合精度较高,特别是z方向,轨道固定模式解算优势更为明显。这主要是因为在轨道松弛模式下解算时,尽管把卫星轨道误差纳入整体解算,获得较高的内符合精度,但在误差分配时把轨道误差引入基线,使得基线、卫星间的误差整体符合度较好,实际计算时,基线间可靠性未必是最有利的,特别是基线的z方向偏差更为突出,导致平差成果整体较轨道固定模式可靠性差。
1.3 星历产品对成果精度的影响星历是影响基线解算的一个重要因素,特别是长基线解算,一般的广播星历难以满足要求,需采用精密星历进行处理。目前国际GNSS服务组织(International GNSS Service, IGS)提供的精密星历产品包括最终精密星历(IGS Final products, IGF)、快速精密星历(IGS Rapid products, IGR)、超快精密星历(IGS Ultra-rapid products, IGU)。不同的星历产品在精度、滞后时间、更新率及采样率方面的差异如表 4[14-15]。
| Satellite ephemerides | Accuracy/cm | Latency | Updates | Sample interval/min |
| IGS | 2.5 | 12~18 days | every Thursday | 15 |
| IGR | 2.5 | 17~41 hours | at 17 UTC daily | 15 |
| IGU | 3.0 | 3~9 hours | at 03, 09, 15, 21 UTC | 15 |
在上述星历产品中,最终精密星历产品精度最高,滞后时间为13 d;快速精密星历精度与超快精密星历精度相当,时延为17 h;超快精密星历每天更新4次,更新时间为每天03:00:00,09:00:00,15:00:00和21:00:00(UTC)。
为了分析不同精密星历产品对成果精度的影响,实验选取最终精密星历、快速精密星历和超快精密星历解算国际全球定位系统服务站的空间直角坐标。实验时除采用的星历产品不同,其它参数设置完全相同。
由表 5可知,采用不同的精密星历,计算国际全球定位系统服务站的坐标成果精度都在毫米级,超快精密星历产品成果的三维坐标分量在7 mm范围内波动,快速精密星历和最终精密星历产品成果在8 mm内波动,在z方向超快精密星历成果偏差稍大,表明3种星历产品计算结果基本相当,这和各星历产品标注的精度基本一致。在相同的观测时段内,相同的数据处理条件下,几种精密星历产品对成果的解算精度影响基本相当。在一定的条件下,可用超快或快速星历替代最终精密星历进行基本等效精度的数据处理。
| Station | Satellite ephemerides | x-bias | y-bias | z-bias |
| BJFS | IGU | -2.8 | 4.6 | 5.5 |
| IGR | -3.0 | 4.6 | 4.7 | |
| IGF | -2.9 | 4.6 | 4.7 | |
| SHAO | IGU | -4.2 | -0.9 | -6.1 |
| IGR | -7.4 | 1.6 | -4.4 | |
| IGF | -7.3 | 1.4 | -4.5 |
全球定位系统基线解算过程中受到多种因素的影响,既存在软件模型误差的影响,也存在基线处理过程中人为因素的干扰,如根据基线残差调整卫星截止高度角、删除错误卫星、调整卫星采样间隔等,相当于基线解算过程既包含系统误差又包含偶然误差。为提高测量成果的精度及可靠性,若采用外业多次观测的处理方式,将导致外业工作量大大增加,同时作业成本进一步提高。众所周知,在一定观测条件下,通过多次观测可以提高观测精度。基于此理论,本文提出观测数据基线多次解算并组合平差的方法,即通过对观测数据进行多次基线解算,并对各次基线成果组合平差。
为验证基线解算次数的影响,文中进行了相关实验。实验中基线解算次数共6次,每次基线独立解算后和前几次基线解算后进行组合平差。实验开始前首先利用TEQC(Translation, Editing and Quality Checking)软件对观测数据进行预处理。实验参数设置为FES2004海潮模型、轨道固定模式,其它参数同前。实验过程中根据成果残差图对部分卫星、部分时段及卫星截止高度角作相应处理,各次基线解算合格后,组合平差坐标与国际全球定位系统服务公布坐标的偏差列于表 6。为更直观地比较基线解算次数间的关系,图 6和图 7给出了BJFS和SHAO站点的坐标偏差与解算成果次数间的关系。
| Station | Number of baseline solution | x-bias | y-bias | z-bias |
| BJFS | 1 | -2.7 | 4.3 | 4.4 |
| 2 | -2.9 | 4.2 | 4.3 | |
| 3 | -2.1 | 2.9 | 4.1 | |
| 4 | -0.8 | 0.5 | 2.4 | |
| 5 | -0.1 | -0.5 | 1.5 | |
| 6 | 0.6 | -0.4 | 0.8 | |
| SHAO | 1 | -7.4 | 1.5 | -4.4 |
| 2 | -7.3 | 1.4 | -3.7 | |
| 3 | -6.9 | 1.2 | -3.6 | |
| 4 | -6.1 | 0.3 | -3.2 | |
| 5 | -5.7 | 0.0 | -2.7 | |
| 6 | -5.3 | -0.4 | -2.6 |
|
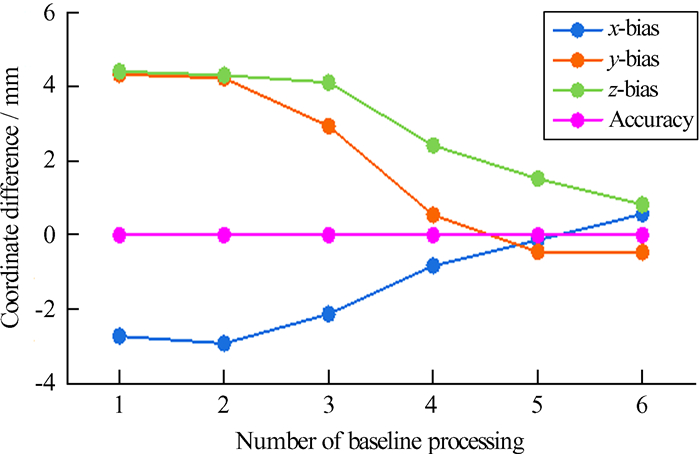
| 图 6 BJFS站基线解算次数与坐标分量偏差关系 Fig. 6 Diagram of the relationship between the number of baseline solutions of BJFS station and the deviation of coordinate components |
|
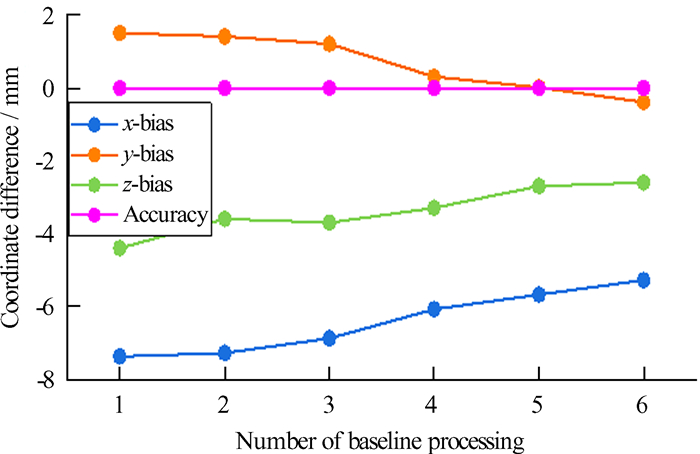
| 图 7 SHAO站基线解算次数与坐标分量偏差关系 Fig. 7 Diagram of the relationship between the number of baseline solutions of SHAO station and the deviation of coordinate components |
由表 6可知,随着基线解算次数的增加,BJFS和SHAO两站点的坐标偏差明显减小,图 6和图 7显示,基线解算4次后成果的精度随基线解算次数的增加不再有明显的提高,这表明基线解算次数增加到一定程度后,点位精度的提升不再显著。实验结论符合偶然误差传播定律中提高测量次数可以提高精度,但当测量次数达到一定的程度后,精度不再明显提高的规律。
为进一步分析多次解算基线组合平差的效果,我们分别采用前文实验中3种不同的精密星历独立解算6次。本次实验除星历不同,其他参数设置完全相同,为了不受人为因素的干扰,基线解算仅仅改变卫星高度角,6次卫星截止高度角设置分别为15°、16°、17°、18°、19°和20°,这样便于检验多次基线解算组合平差的可靠性。限于篇幅,实验结果直接给出BJFS和SHAO两国际全球定位系统服务站中解算次数计算结果与国际全球定位系统服务站公布成果比较的关系图。不同星历及解算次数关系见图 8~图 13。

|
| 图 8 BJFS站超快精密星历基线解算次数与坐标分量偏差关系 Fig. 8 Diagram of the relationship between the number of IGU ephemeris baseline solutions of BJFS station and the deviation of coordinate components |
|
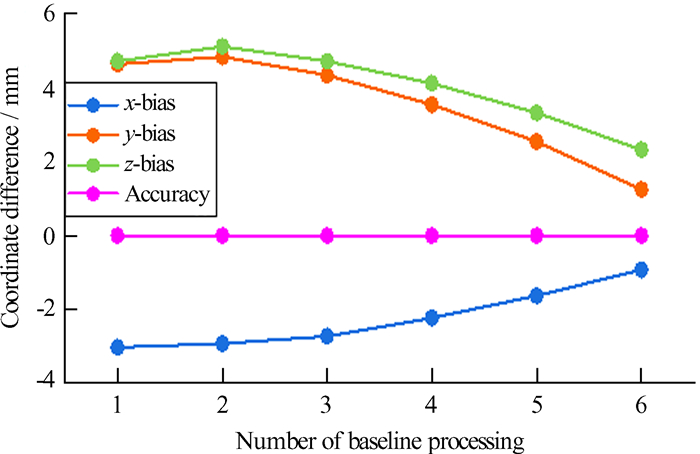
| 图 9 BJFS站快速精密星历基线解算次数与坐标分量偏差关系 Fig. 9 Diagram of the relationship between the number of IGR ephemeris baseline solutions of BJFS station and the deviation of coordinate components |
|
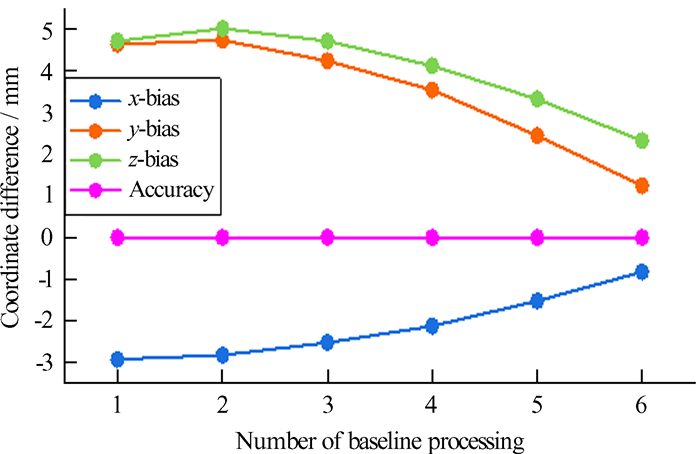
| 图 10 BJFS站最终精密星历基线解算次数与坐标分量偏差关系 Fig. 10 Diagram of the relationship between the number of IGF ephemeris baseline solutions of BJFS station and the deviation of coordinate components |
|
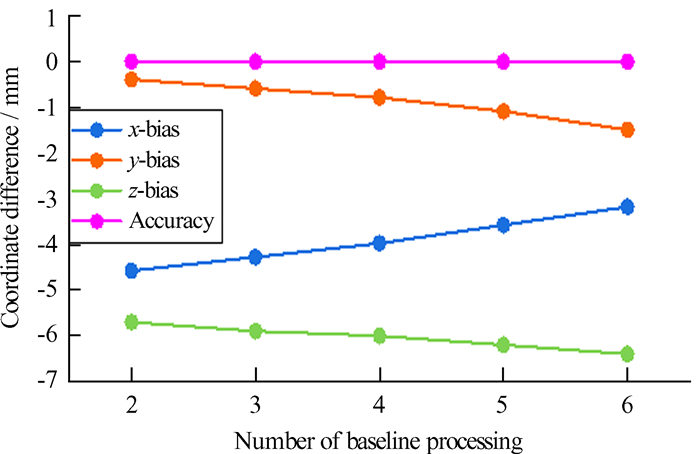
| 图 11 SHAO站超快精密星历基线解算次数与坐标分量偏差关系 Fig. 11 Diagram of the relationship between the number of IGU ephemeris baseline solutions of SHAO station and the deviation of coordinate components |
|
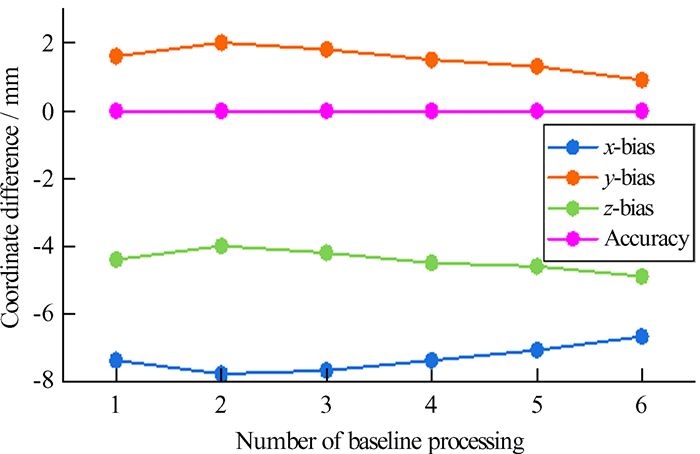
| 图 12 SHAO站快速精密星历基线解算次数与坐标分量偏差关系 Fig. 12 Diagram of the relationship between the number of IGR ephemeris baseline solutions of SHAO station and the deviation of coordinate components |

|
| 图 13 SHAO站最终精密星历基线解算次数与坐标分量偏差关系 Fig. 13 Diagram of the relationship between the number of IGF ephemeris baseline solutions of SHAO station and the deviation of coordinate components |
由图 8~图 13可知,采用3种精密星历中的任意一种,随着基线解算次数的增加,BJFS站的精度明显提高,x,y和z坐标分量的偏差均随着基线解算次数的增加而降低,表现出良好的收敛性;而SHAO站各坐标分量随着基线解算次数的增加有收敛也有发散,整体有所收敛。一方面说明增加基线解算次数进行组合平差可以提高成果的精度及可靠性,另一方面表明,仅靠设置卫星截止高度角解算基线不尽完美,在实际工作中应结合基线残差图、卫星截止高度角、变换卫星采样间隔及过滤几何因子不理想的时段等方式,进一步提升基线多次组合解算的效果。
2 结论本文在实验海潮模型对基线及坐标成果影响的基础上,分析了轨道模式及不同精密星历对成果精度的影响,验证了轨道松弛和轨道固定解算模式的内外符合精度的可靠性。在此基础上,提出了基线多次解算组合平差的方法,通过不同海潮模型、轨道设置模式、星历产品及基线多次解算的实验分析,得出以下结论:
(1) 使用海潮模型比未用海潮模型解算获得的基线及坐标偏差等精度指标更优,FES2004海潮模型解算结果的内外符合精度整体较优,且FES2004模型的分辨率较其它模型更高,因而可以更好地减少模型内插的误差影响,在使用海潮模型计算时,应优先考虑。
(2) 使用轨道松弛模式解算时,解算结果往往内符合精度较高,外部可靠性在空间直角坐标系中较轨道固定模式差。主要原因是该模式把星历误差作为未知数进行联合求解,易把相关误差调整到基线中,造成基线内符合精度高,外符合精度较轨道固定模式差的现象,在一般工程中建议使用轨道固定模式进行基线解算。
(3) 最终精密星历、快速精密星历及超快精密星历解算成果精度基本相当,几种星历产品公布的精度也基本相当,说明在数据处理过程中,可以使用快速精密星历或超快精密星历替代最终精密星历,获得等效精度的数据成果。
(4) 同一组观测数据,经合理增加基线解算次数组合平差的方法,较单次基线计算成果精度高,说明增加基线解算次数进行组合平差,能有效提高数据解算精度和可靠性,值得在全球定位系统数据处理过程中推广及进一步验证。
| [1] |
高旺, 高成发, 潘树国, 等. 基于快速星历的GAMIT高精度基线解算研究[J]. 测绘科学, 2015, 40(2): 22–25, 38 GAO W, GAO C F, PAN S G, et al. GAMIT high-precision baseline-solution method based on the rapid ephmeris-IGS and IGU[J]. Science of Surveying and Mapping, 2015, 40(2): 22–25, 38. |
| [2] |
李星光, 郑南山. 参数设置对高精度GPS数据解算的影响探讨[J]. 测绘科学, 2015, 40(1): 33–37, 51 LI X G, ZHENG N S. Discussion on effects of different parameter settions on high-precise GPS data solution[J]. Science of Surveying and Mapping, 2015, 40(1): 33–37, 51. |
| [3] |
邬熙娟, 高俊强, 黄燕. 小区域GPS网GAMIT解算结果与IGS站选取的关系[J]. 南京工业大学学报(自然科学版), 2010, 32(4): 96–99 WU X J, GAO J Q, HUANG Y. Relationship between GAMIT processing results of small GPS regional net and determination of IGS stations[J]. Jourmal of Nanjing University of Echnology (Natural Science Edition), 2010, 32(4): 96–99. |
| [4] |
万军, 成英燕, 党亚民, 等. 陆态网测站高精度解算分区方案[J]. 测绘科学, 2016, 41(4): 1–4 WAN J, CHENG Y Y, DANG Y M, et al. Partition scheme research on high accuracy solution of crustal movement observation network of China[J]. Science of Surveying and Mapping, 2016, 41(4): 1–4. |
| [5] |
黄祖登, 梅连辉. 高精度GPS数据处理中对流层参数估计研究[J]. 测绘地理信息, 2013, 38(5): 12–15 HUANG Z D, MEI L H. Research on the time selection of PWL in high-precision GPS data processing[J]. Journal of Geomatics, 2013, 38(5): 12–15. |
| [6] |
曹艳丰, 陈宝献, 陈秀万, 等. 基于GPS数据的MODIS大气可降水量反演精度提高模型[J]. 遥感信息, 2014, 29(2): 21–25 CAO Y F, CHEN B X, CHEN X W, et al. A real-time accuracy model of MODIS PWV using GPS PWV data[J]. Remote Sensing Information, 2014, 29(2): 21–25. |
| [7] |
张光茹, 秘金钟. 不同数据处理策略对PPP收敛精度的影响[J]. 测绘科学, 2018, 43(3): 77–81 ZHANG G R, BEI J Z. Impact analysis of different data processing strategies for PPP convergence accuracy[J]. Science of Surveying and Mapping, 2018, 43(3): 77–81. |
| [8] |
曹炳强, 成英燕, 许长辉. 海潮模型对连续跟踪参考站数据解算的影响-以福建省为例[J]. 测绘科学, 2015, 40(12): 108–111 CAO B Q, CHENG Y Y, XU C H. Discussion of CORS data-sovling influenced by ocean tide loading models[J]. Surveying and Mapping, 2015, 40(12): 108–111. |
| [9] | URSCHL C, DACH R, HUGENTOBLER U, et al. Validating ocean tide loading models using GPS[J]. Journal of Geodesy, 2005, 78(10): 616–625. DOI: 10.1007/s00190-004-0427-9 |
| [10] | MATSUMOTO K, TAKANEZAWA T, OOE M. Oceantide models developed by assimilating TOPEX/POSEIDON altimeter data into Hydrodynamical Model: a global model and a regional model around Japan[J]. Journal of Oceanography, 2000, 56(5): 567–581. |
| [11] | LYARD F, LEFEVRE F, LETELLIER T, et al. Modelling the global ocean tides: modern insights from FES2004[J]. Ocean Dynamics, 2006, 56(5/6): 394–415. |
| [12] | WANG Y H, FANG G H, WEI Z X, et al. Accuracy assessment of global ocean tide models base on satellite altimetry[J]. Advances in Earth Science, 2010, 25(4): 353–359. |
| [13] | 孙佳龙, 郭金运, 郭淑艳, 等. 基于验潮资料的CSR4.0模型和NAO. 99b模型在中国海域的精度分析, 2013, 28(5): 2787-2795. SUN J L, GUO J Y, GUO S Y, et al. Accuracy analysis of CSR4.0 and NAO. 99b over China seas by tidal data[J]. Progress in Geophysics, 2013, 28(5): 2787-2795. |
| [14] |
刘盼, 刘智敏, 张明敏, 等. 不同IGS星历产品对地基GPS反演水汽的影响[J]. 测绘科学, 2018, 43(12): 17–22 LIU P, LIU Z M, ZHANG M M, et al. Influence of different IGS ephemeris products on GPS of precipitable water vapor inversion[J]. Science of Surveying and Mapping, 2018, 43(12): 17–22. |
| [15] |
师芸, 申靖宇, 邬康康, 等. 不同精密星历对震时高频GNSS解算结果精度分析[J]. 全球定位系统, 2019, 44(6): 81–85 SHI Y, SHEN J Y, WU K K, et al. Accuracy analysis of high-precision GNSS solution results for different precise ephemeris[J]. GNSS World of China, 2019, 44(6): 81–85. |


