在现实情况下,由于重力、温度、风载等因素的影响,射电望远镜需要通过主动主反射面(简称主动面)调整技术修正面型误差[1]。主动面调整技术是通过对分块拼接而成的主反射面面板进行位置调整来修正表面形状,而高精度位移促动器是实现反射面误差主动修正的关键[2]。当前世界上应用主动面技术的全可动射电望远镜主要有美国绿岸射电天文望远镜(Green Bank Telescope, GBT)[3]、墨西哥大型毫米波望远镜(Large Millimeter Telescope, LMT)[4]、意大利撒丁岛射电望远镜(Saladin Radio Telescope, SRT)[5]、中国天马望远镜(Tian Ma Telescope)[6]等。本文的促动器专门针对即将建设的新疆奇台110 m全向可动射电望远镜。
不同于其他地方,新疆奇台的气候条件较为恶劣,温度变化范围广,且变化剧烈。对于110 m射电望远镜所采用的促动器来说,需要在-40~60 ℃的范围内保持促动器的定位精度在±15 μm,从而实现反射面全天候高精度调整的要求。由于单靠机械结构与位移传感器无法消除热误差带来的影响,因此,需要找到一种方法修正由于热误差带来的定位精度的影响。
建立热误差补偿的预测模型取决于促动器温度场分布的准确测量。然而,为了准确获得温度场,就必须在促动器上放置大量温度测点,这些温度测量会增加计算和测量的工作量,增加模型建立的复杂度,并影响促动器的正常运行。
灰色预测法是对灰色系统进行预测的一种方法,通过鉴别影响系统因素之间的发展趋势进行关联分析,对系统的某一特征量进行预测,构造预测对象特征的灰色预测模型。根据文[7-8]的灰色系统理论,导致机械加工的热误差受复杂因素影响,表现出明显的灰色性质。
因此,本文从最可能影响促动器定位精度的多个温度点出发,在多个温度测量点中选择关键温度测点,以减少测量点的数量,并优化促动器上的热传感器位置;在避免温度变量过多引起的热误差模型中的重复共线性的同时,提高热误差建模的鲁棒性;运用灰色预测理论进行建模,并依据实际情况调整建模模型,使得望远镜在-40~60 ℃运行的情况下,能够达到要求的精度。
1 温度测量点的选择与筛选对于一个复杂的机械系统,难以采用数学方式直接得出最佳的温度测量点。一般来说,依据工程经验判断最有可能的影响方式,再结合机械结构进行一系列温度测量点位的分布设计,通过实验数据与统计相关的分析减少温度测量点的选择,最终达到简化建模过程,提高模型准确率与鲁棒性的效果。
1.1 温度测量点的选择与分布对用于110 m射电望远镜的促动器,主要采用步进电机加蜗轮蜗杆的结构,蜗杆顶部的位移精度代表着整个促动器的精度。
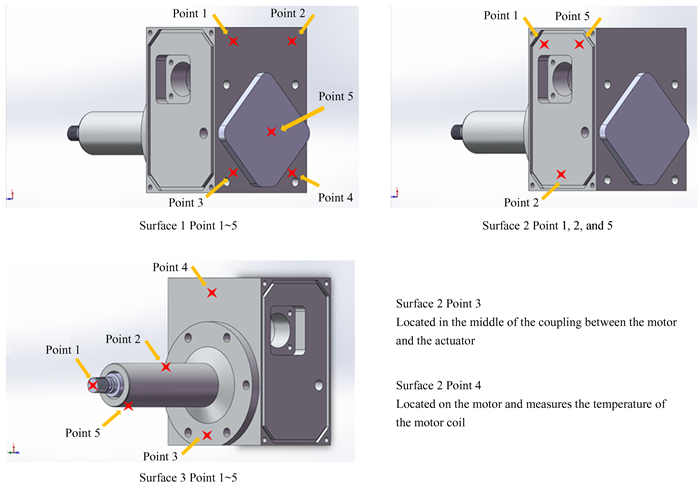
从工程经验来说,可能影响促动器精度的温度有环境温度、步进电机的温度、蜗轮温度、蜗杆温度、花键套温度等,结合可以实际测量的促动器的点位,温度测量点可以分布在促动器的3个面,外加1个环境温度,总共16个点位。促动器面与点的分布如图 1,其中,
|
| 图 1 温度测量点点位 Fig. 1 Temperature measurement points |
面1:点1~点5综合表征促动器蜗轮温度分布对促动器位移的影响;
面2:点1、点2和点5综合表征步进电机温度分布对促动器位移的影响,点3直接测得电机联轴节部分温度,点4直接测得电机外壳温度;
面3:点1直接测得蜗杆顶端附近的温度,点2~点5综合表征花键套温度分布对促动器的影响。
在测试促动器的精度时,促动器需要放在实验台上,在促动器蜗杆前端装有光栅尺,用于测量促动器的位移。测试环境为恒温恒湿箱,并且默认室温(20 ℃)时的位移为0。实验情况与实验结果如图 2。

|
| 图 2 实验情况与实验结果 Fig. 2 Experimental situation and experimental results |
温度测量点的筛选主要有3个参考标准:
(1) 温度与位移之间有高相关性,采用皮尔逊相关系数(Pearson Correlation Coefficient, PCC),ρT, S=COV(S, T)/(σSσT),即温度与位移之间的协方差和标准差的商进行计算,ρT, S越接近1,线性关系越密切。各点相关系数如表 1。
| Surface 1 | Surface 2 | Surface 3 | |
| Point 1 | 0.996 | 0.984 | 0.977 |
| Point 2 | 0.996 | 0.997 | 0.989 |
| Point 3 | 0.996 | 0.986 | 0.972 |
| Point 4 | 0.996 | 0.978 | 0.966 |
| Point 5 | 0.993 | 0.978 | 0.989 |
| Ambient temperature | 0.943 | ||
(2) 在测试中当位移达到0 μm时,温度测量点显示的温度应在20 ℃左右。各点测试所得温度如表 2。
| Surface 1 | Surface 2 | Surface 3 | |
| Point 1 | 23.9 | 22.4 | 25.6 |
| Point 2 | 23.9 | 20.6 | 20.9 |
| Point 3 | 23.6 | 21.6 | 27.8 |
| Point 4 | 20.7 | 16.6 | 28.5 |
| Point 5 | 21.1 | 15 | 18.7 |
(3) 方便安装且不影响促动器正常工作
在暂时不考虑第3点的情况下,针对促动器上的15个温度测试点、环境温度与位移之间的相关性如表 1,考虑到实验要求的精度高,需要皮尔逊相关系数越接近1越好。
在考虑相关性时,同时考虑测试点温度达到室温时的位移,如表 2。在实验中促动器位移回0的时刻,测试点的温度并不一定回到室温,由于无论是实验还是建模均是以室温时的位移为0作为前提进行的,相差过大必然影响建模。因此,综合参考标准和表 1、表 2,最后得到可以使用的5个温度测量点分别为:面1点4、面1点5、面2点2、面2点3和面3点2。
1.3 温度测试点的统计筛选在统计学中,显著性检测常用来检测样本与总体之间的差异水平。在本次实验中,采用显著性检测来筛选温度点,可以比较各个温度点所测得的温度与所对应的位移之间的可信程度,一般来说,显著性水平采用5%与1%,并用
| $ t=|\rho |\sqrt{(n-2)/\left( 1-{{\rho }^{2}} \right)}\ \ \ \ |t|>{{t}_{\alpha /2}}(n-2) $ | (1) |
进行计算。显著性水平越小,则差异越小,可信度越高。
通过基本要求进行筛选后得到的5个点:面1点4、面1点5、面2点2、面2点3和面3点2,重新编号为P1~P5。对P1~P5进行回归分析,并采用显著性检验,分别以0.05与0.01为阈值筛选自变量,最终可以得到两个线性模型。
如表 3,通过回归分析得到两个模型,其中B表示未标准化的回归系数,Beta表示标准化的回归系数,如果显著性以0.01为阈值,则得到只与P3点温度相关的模型1,如果显著性以0.05为阈值,则得到与P1和P3点温度相关的模型2。
| Model | B | Standard error | Beta | t | Significance | |
| 1 | Constant | -80.259 μm | 0.971 | -82.667 | 0.000 | |
| P3 | 3.561 μm/K | 0.033 | 0.995 | 108.258 | 0.000 | |
| 2 | Constant | -80.188 μm | 0.958 | -83.735 | 0.000 | |
| P3 | 2.156 μm/K | 0.685 | 0.603 | 3.147 | 0.002 | |
| P1 | 1.410 μm/K | 0.687 | 0.393 | 2.052 | 0.043 |
如表 4,在回归分析中存在剔除的变量,其中,偏相关值一般介于-1与1之间,绝对值越大,表明该变量对因变量影响越大,而共线性容差是用来说明自变量之间的共线性关系,一般来说,低于0.1则共线性较强。因此,通过显著性、偏相关与共线性等多种因素筛选自变量,最终得到可以用于模型的自变量。
| Model | Beta | t | Significance | Partial correlation | Collinear tolerance | |
| 1 | P1 | 0.393 | 2.052 | 0.043 | 0.193 | 0.002 |
| P2 | 0.278 | 0.729 | 0.468 | 0.070 | 0.001 | |
| P4 | 0.061 | 1.470 | 0.144 | 0.139 | 0.049 | |
| P5 | 0.302 | 1.998 | 0.048 | 0.188 | 0.004 | |
| 2 | P2 | 0.459 | 1.119 7 | 0.234 | 0.114 | 0.001 |
| P4 | -0.205 | -1.544 | 0.125 | -0.147 | 0.005 | |
| P5 | 0.070 | 0.137 | 0.892 | 0.013 | 0.000 |
模型1表明,促动器的精度可以完全由P3点的温度表示,模型2表明,促动器的精度可以完全由P1和P3点温度的线性组合表示。对比模型1与模型2,从P1和P3的显著性可以看出,如果只采用P3点进行温度测量,得到的模型更加精确。
从促动器结构方面看,P3点距离电机、蜗轮与蜗杆底部均较近,可以综合各个关键部位的温度影响,这也是为什么用P3点表征促动器受温度影响产生的位移变化有较好效果的原因之一。另外,P3点在实际安装与工作中不会对促动器本身产生影响,也符合基本要求的第3点。因此,在接下来的建模中,只采用P3点,即促动器的面2点2进行建模。
2 模型建立与运用灰色系统理论是根据过去及现在已知或不确定的信息建立一个由过去引伸到未来的灰色模型, 从而确定系统未来发展变化的趋势。灰色系统理论以微分方程为工具, 能够反映事物发展的本质,不需要对预测系统有明确的了解, 其研究数据可随机产生[9],因此,相对传统统计研究方法,灰色预测模型具有能够研究小样本、贫信息、任意分布数据的优点。
2.1 灰色预测模型的建立由实验数据展示的图 2可以发现,如果只采用线性模型进行误差补偿,难以得到好的补偿结果。在实验中,若能利用较少的或不确切的表示灰色系统行为特征的原始数据序列,来描述灰色系统内部事物连续变化的过程,可以采用灰色预测模型计算。由于对热误差的研究所采集的数据符合小样本、贫信息的特点,而且在庞大的机械系统中,也无法确定热误差直接相关的因素,所以,灰色系统理论更加适用于热误差建模的研究。
在实验过程中,随着温度的变化,促动器的精度每变化5 μm采集一次温度数值。用S代表促动器的位移,单位为μm,ΔS表示位移的变化量,T(0)(t)表示温度的观测值,单位为K,从ΔS=0 μm开始记为t=0,温度记为T(0)(0),ΔS=5 μm时记为t=1,温度记为T(0)(1),以此类推,因此有
| $ S=5t-{{B}_{\text{t}}}, $ | (2) |
其中,常数Bt由T(0)=293.15 K时的位移S决定,即保证在室温下促动器的位移为0。经过实验可以确定Bt=210 μm。
在实验中T(0)={T(0)(0),T(0)(1), T(0)(2),…,T(0)(N)}为温度的观测值, 运用灰色预测时,需要对观测值进行一次累加,得到累加值T(1)={T(1)(0),T(1)(1), T(1)(2),…,T(1)(N)},其中T(1)(n)=
| $ {{T}^{(1)}}(k)=\left[ {{T}^{(1)}}(0)-u/a \right]{{\text{e}}^{-aK}}+u/a, $ | (3) |
采用最小二乘法估计求解a和u:
| $ \left[ \begin{matrix} a \\ u \\ \end{matrix} \right]={{\left( {{B}^{\text{T}}}B \right)}^{-1}}{{B}^{\text{T}}}\left[ \begin{matrix} {{T}^{(0)}}(1) \\ \vdots \\ {{T}^{(0)}}(N) \\ \end{matrix} \right], $ | (4) |
| $ B=\left[ \begin{matrix} -\frac{1}{2}\left[ {{T}^{(1)}}(1)+{{T}^{(1)}}(0) \right] & 1 \\ \vdots & \vdots \\ -\frac{1}{2}\left[ {{T}^{(1)}}(N)+{{T}^{(1)}}(N-1) \right] & 1 \\ \end{matrix} \right]. $ | (5) |
因此,通过灰色预测得到的预测值为
| $ T(k)={{T}^{(1)}}(k)-{{T}^{(1)}}(k-1);\ T(0)={{T}^{(1)}}(0). $ | (6) |
联立(1),(3),(5)式可解得
| $ S=-K/a\ln (T)+B+K/a\ln \left\{ \left[ {{x}^{(1)}}(1)-u/a \right]\left( {{\text{e}}^{a}}-{{\text{e}}^{2a}} \right){{\text{e}}^{-at}} \right\}, $ | (7) |
其中,T为温度,单位为K。为了简便可以记
| $ {{K}_{y}}=-K/a, $ | (8) |
| $ {{B}_{y}}=B+K/a\ln \left\{ \left[ {{x}^{(1)}}(1)-u/a \right]\left( {{\text{e}}^{a}}-{{\text{e}}^{2a}} \right){{\text{e}}^{-at}} \right\}, $ | (9) |
其中,Ky与By的单位均为μm。将实验数据整体代入(7)、(8)、(9)式进行灰色预测,可以得到
| $ S={{K}_{y}}\ln (T)+{{B}_{y}}=1063.8298\ln (T)-6043.28137. $ | (10) |
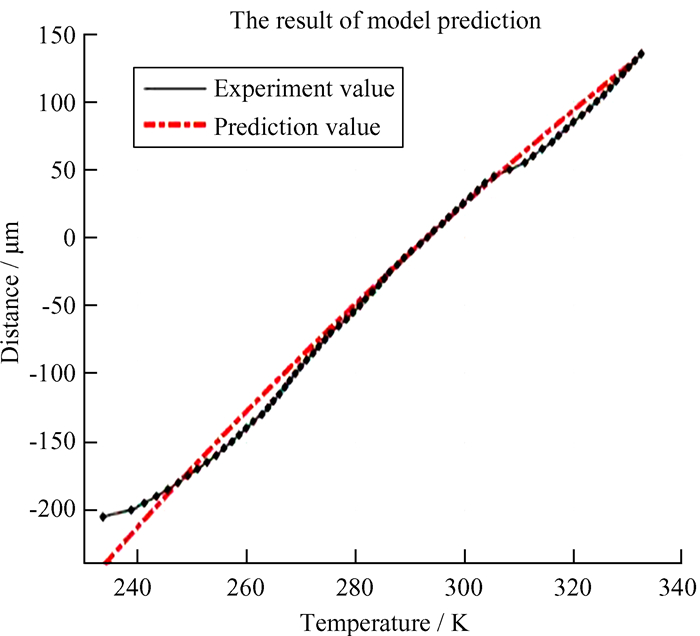
灰色预测模型与实验数据的对比如图 3,其中红线为灰色预测模型的结果,黑线为实验结果。预测模型在0~40 ℃的范围内与实验模型吻合较好,在极端温度下有一定误差。在实际工作中,模型误差的存在使得实时控制出现误差,导致误差不断积累,因此,有必要将理论模型代入促动器进行实时调控,再根据实际情况进行模型修改。
|
| 图 3 灰色预测模型预测结果与实验结果对比 Fig. 3 Prediction results and experimental results |
在完成模型预测后,将模型写入程序,对原促动器进行实时调节。在第1次实验中,采用(10)式进行实时误差调节,得到的结果如表 5的第1次实验和图 4(a)。通过实验可以看出,通过灰色理论直接得到的灰色模型在实际应用时,由于模型无法完全修正误差,导致误差不断累积,使得越偏离室温,位移误差越大。在调整并重新进行实验时,需要对公式进行修改,最直接有效的方法是对公式分段处理。
| Test_1 | |||
| Temperature range/K | y | Ky/μm | By/μm |
| 233.15~333.15 | 1 | 1 063.829 8 | -6 043.281 37 |
| Test_2 | |||
| Temperature range/K | y | Ky/μm | By/μm |
| 233.15~253.15 | 1 | 625.039 7 | -3 604.449 06 |
| 253.15~273.15 | 2 | 924.747 1 | -5 263.024 48 |
| 273.15~313.15 | 3 | 1 063.829 8 | -6 043.281 37 |
| 313.15~333.15 | 4 | 1 256 | -7 147.622 45 |
| Test_3 | |||
| Temperature range/K | y | Ky/μm | By/μm |
| 233.15~273.15 | 1 | 825 | -4 703.441 15 |
| 273.15~313.15 | 2 | 1 063.829 8 | -6 043.281 37 |
| 313.15~333.15 | 3 | 1 256 | -7 147.622 45 |
| Test_4 | |||
| Temperature range/K | y | Ky/μm | By/μm |
| 233.15~273.15 | 1 | 825 | -4 698.940 76 |
| 273.15~285.15 | 2 | 836.9 | -4 765.700 02 |
| 285.15~313.15 | 3 | 1 253.8 | -7 122.442 13 |
| 313.15~333.15 | 4 | 1 256 | -7 135.084 83 |
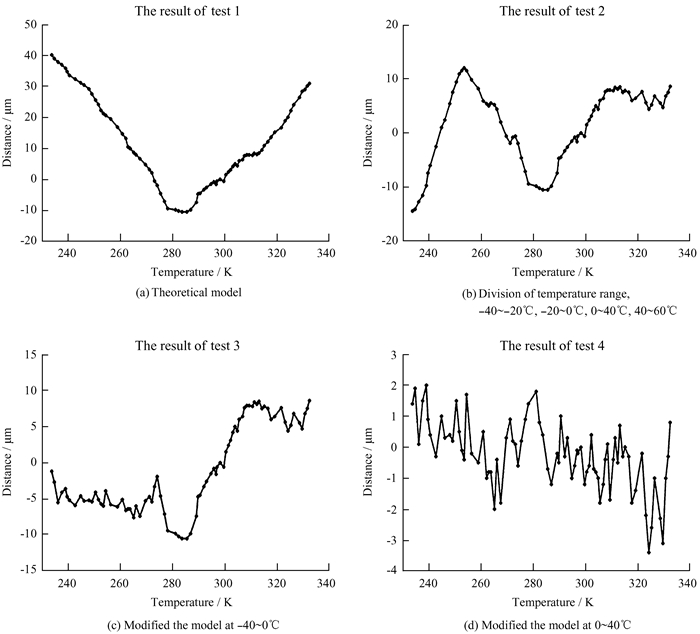
|
| 图 4 灰色预测模型各实验情况下结果 Fig. 4 Results of the gray prediction model in each case |
可以看到,在不同的温度段,误差可以看作线性增减,而且由于dS/dT=Ky/T,并且在相同趋势的温度范围内可以进行近似处理,用Ty与Ty+1表示y温度范围内的温度下限与上限,ΔSy表示y温度范围内需要调节的位移量,因此有
| $ \begin{align} & \Delta {{S}_{y}}=\int_{{{T}_{y}}}^{{{T}_{y+1}}}{\Delta }{{K}_{y}}/T~\text{d}T=\left[ 2\Delta {{K}_{y}}/\left( {{T}_{y1}}+{{T}_{y2}} \right)+\cdots \right. \\ & \ \ \ \ \ \ \ \ \ \ \left. +2\Delta {{K}_{y}}/\left( {{T}_{y(n-1)}}+{{T}_{yn}} \right) \right]\left( {{T}_{y+1}}-{{T}_{y}} \right) \\ & \ \ \ \ \ \ \ \ \ \ \approx \Delta {{K}_{y}}\left( {{T}_{y+1}}-{{T}_{y}} \right)/{{T}_{y}}, \\ \end{align} $ | (11) |
根据(11)式可以计算修正后的
| $ \overline{{{K}_{y}}}={{K}_{y}}-\Delta {{K}_{y}} $ | (12) |
| $ \left\{ {\begin{array}{*{20}{c}} {\overline {{B_y}} = - \overline {{K_y}} \ln 293.15}\\ {{\rm{ 当 }}y{\rm{区间内包含室温}}}\\ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {\overline {{K_{y - 1}}} \ln {T_y} + \overline {{B_{y - 1}}} = \overline {{K_y}} \ln {T_y} + \overline {{B_y}} }\\ {\overline {{K_y}} \ln {T_{y + 1}} + \overline {{B_y}} = \overline {{K_{y + 1}}} \ln {T_{y + 1}} + \overline {{B_{y + 1}}} }\\ {} \end{array}} \right.\\ {\rm{当 }}y{\rm{区间内不包含室温}} \end{array} \end{array}} \right. $ | (13) |
在接下来的数次实验中,分别针对不同温度区间进行修正。在第2次实验中,将温度区间分为-40~-20 ℃,-20~0 ℃,0~40 ℃,40~60 ℃,得到的结果如表 5的第2次实验与图 4(b);在第3次实验中,修正-40~0 ℃区间内的模型,得到的结果如表 5的第3次实验与图 4(c);在第4次实验中,修正0~40 ℃区间内的模型,得到的实验结果如表 5的第4次实验与图 4(d)。
通过多次验证实验,在第4次实验中,将促动器由热误差引起的精度减小到±4 μm,满足110 m射电望远镜对促动器精度的要求。
3 结论本文针对即将用于新疆奇台110 m射电望远镜的促动器进行热误差补偿。110 m射电望远镜要求促动器可以在-40~60 ℃的范围内保持±15 μm的精度。本文针对促动器由于温度变化带来精度上的变化进行误差补偿,最终将由于温度变化引起的精度的变化量减小到±4 μm。促动器结构复杂,热误差影响因素繁多,仅从理论上计算合适的温度测量点或模型不太可能。本文创新地采用工程实践经验与统计学相结合的方法筛选温度测量点,并且在模型建立后,与实验相结合推导了适用于该模型修改的公式,为之后在射电望远镜促动器上的研究提供参考。
| [1] |
李宁, 刘志勇, 王娜, 等. 高精度天线指向控制算法的研究[J]. 天文研究与技术, 2017, 14(4): 414–420 LI N, LIU Z Y, WANG N, et al. Research of control algorithm for antenna high pointing accuracy[J]. Astronomical Research & Technology, 2017, 14(4): 414–420. |
| [2] |
张宗猛, 王正兰, 杨德华, 等. 基于步进电机的位移促动器设计与实测[J]. 天文研究与技术, 2019, 16(3): 329–334 ZHANG Z M, WANG Z L, YANG D H, et al. Development and test of a stepper motor driven displacement actuator[J]. Astronomical Research & Technology, 2019, 16(3): 329–334. |
| [3] | PRESTAGE R M, CONSTANTIKES K T, HUNTER T R, et al. The Green Bank Telescope[J]. Proceedings of the IEEE, 2009, 97(8): 1382–1390. DOI: 10.1109/JPROC.2009.2015467 |
| [4] | HUGHES D H, JUAN-CARLOS JAUREGUI CORREA, SCHLOERB F P, et al. The Large Millimeter Telescope status[C]//Proceedings of SPIE. 2010. |
| [5] | ORFEL A, MORISIANI M, ZACCHIROLI G, et al. An active surface for large reflector antennas[J]. IEEE Antennas & Propagation Magazine, 2004, 46(4): 11–19. |
| [6] | DONG J, JING H L, YE Q, et al. The active surface control system for the Tian Ma Telescope[C]//Proceedings of SPIE. 2016. |
| [7] | DENG J L. Introduction to Grey system theory[J]. Journal of Grey System, 1989(1): 1–24. |
| [8] |
邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002: 171-201. DENG J L. Grey theory[M]. Wuhan: Huazhong University of Science & Technology Press, 2002: 171-201. |
| [9] | LUO Y X, GUO H X, ZHANG L T, et al. Grey reliability design model and its application to mechanical engineering[J]. Journal of National University of Defense Technology, 2002, 24(1): 94–99. |


