2. 昆明理工大学云南省计算机技术应用重点实验室, 云南 昆明 650500
2. Key Laboratory of Applications of Computer Technology of the Yunnan Province, Kunming University of Science and Technology, Kunming 650500, China
宇宙再电离、脉冲星、寻找外星智慧生命体等科学研究是当前天文领域的研究热点,要实现这些研究目标,迫切需要射电望远镜具有更高的灵敏度和分辨率。国际大科学工程——平方公里阵列是人类有史以来建造的最大射电望远镜,信号接收总面积约1 km2,具有高灵敏度,高时间、高空间、高频率分辨率,高动态范围的特点,它的建成将给天文学研究带来革命性的影响。
校准是射电干涉测量的重要组成部分,实际观测过程中,电离层、温度、地面环境变化,电子元件的噪声和背景温度等造成天线增益的变化[1-2]。天线增益校准的准确性是影响复可见度数据准确性的主要因素[3]。针对极为微弱且错综复杂的各类系统与环境效应的校准是困扰当前平方公里阵列科学研究的关键因素,为了提高成像精度和动态范围,保证成像的动态范围达到106以上[4],天线增益的校准成为需要深入研究的课题。
射电天文仿真校准成像软件库是射电天文数据处理专家为平方公里阵列研制的数据处理软件,开发语言为Python,有良好的可读性,利于后续计算机专家对算法进行并行实现和部署。为符合RASCIL的编程规定,本文基于Python语言,实现了经典的天线增益校准算法Antsol,并对其进行了性能优化。
1 天线增益校准算法在过去的几十年中,针对射电干涉阵成像动态范围受校准精度制约的问题,科学家们给予了相当大的关注,并在增益校准算法上取得了一定的成果[5-9]。文[5-6]讨论分析了甚大阵(Very Large Array, VLA)数据校准过程中的误差,给出了利用最小二乘法求解天线增益的经典算法——Antsol算法,该算法对可见度数据的异常值比较敏感。文[7]提出了一种鲁棒性更好的求解增益的方法,与Antsol相比,这种方法受异常值的影响较小,同时性能与Antsol相当。文[8]基于最小二乘法提出了4种从协方差矩阵求解天线增益的算法,并用韦斯特博克综合孔径射电望远镜(Westerbork Synthesis Radio Telescope, WSRT)的实验数据进行了仿真测试。文[9]提出了一种较新的算法StEFCal(Statistically Efficient And Fast Calibration),该算法在低频阵列(Low Frequency Array, LOFAR)数据校准管线的几个阶段得到了应用。Antsol算法至今仍在大型米波射电望远镜(Giant Metrewave Radio Telescope, GMRT)和通用天文软件包(Common Astronomy Software Applications, CASA)中使用,是天文图像处理系统(Astronomical Image Processing System, AIPS)的默认算法,因此SKA-RASCIL必须有该算法的高性能实现。
2 天线增益校准算法的基本原理在综合孔径成像中,不同天线接收的信号通过乘法电路和时间平均电路进行合成并输出。乘法电路和时间平均电路组成相关器,干涉阵的每个相关器的输出为天线信号和系统噪声的总和。对于天线p和q组成的天线对,相关器的输出为
| $ \rho _{pq}^{{\rm{obs}}} = {g_p}g_q^*\rho _{pq}^{\rm{o}} + {\varepsilon _{pq}}, $ | (1) |
其中,ρpqobs为天线p,q组成的基线观测到的可见度;ρpqo为模型可见度(通常是一个点源模型);εpq为由天线p,q组成的基线的叠加噪声;gp和gq*分别为天线p的复增益因子和天线q的复增益因子的共轭复数。对于任意天线k,增益可表示为
| $ {g_k} = \left| {{g_k}} \right|{{\rm{e}}^{ - {\rm{i}}\varphi k}}, $ | (2) |
其中,|gk|为天线接收信号的幅值;φ为信号基于天线的相位。因此,p,q天线对的复增益为
| $ {G_{pq}}{\rm{ = }}{g_p}g_q^*, $ | (3) |
给定ρpqobs并且已知模型可见度ρpqo,就可以求解天线对的复增益Gpq。假设天线对的复增益是独立的,且符合高斯概率密度函数(这意味着实部和虚部是独立的高斯随机过程),可以通过求给定函数S的最小值估计gp,
| $ S = \sum\limits_{\begin{array}{*{20}{c}} {p, q}\\ {p \ne q} \end{array}} {{{\left| {{G_{pq}} - {g_p}g_q^*} \right|}^2}} {w_{pq}}, $ | (4) |
其中,wpq为权重值。将S分别对(4)式中复增益的实部gpR、虚部gpI求偏导数并令其为0,合并实部、虚部:
| $ {{g}_{p}}=\frac{\sum\limits_{\begin{smallmatrix} q \\ q\ne p \end{smallmatrix}}{{{G}_{pq}}{{g}_{q}}}}{\sum\limits_{\begin{smallmatrix} q \\ q\ne p \end{smallmatrix}}{{{\left| {{g}_{q}} \right|}^{2}}}}. $ | (5) |
增益校准的残差rpq为
| $ {{r_{pq}} = {G_{pq}} - {g_p}g_q^*.} $ | (6) |
为了提高校准的精度,要求残差收敛得尽可能小,需要对(5)式进行多次迭代求解。
3 Antsol算法的实现Antsol算法已经有Fortran和C语言的实现版本。本文参考美国甚大阵的Fortran程序(Thomspon经典书籍的附录1[5]),并使用Python语言对Antsol算法进行高性能实现。同时,由于SKA-SDHP采用了DASK(https://www.dask.org)作为多任务分布计算框架,而DASK库可以将计算扩展到多个内核甚至多个机器,在天线增益校准软件模块开发时,我们不需要在模块内使用多任务并行计算,同时,为了使软件具有更好的通用性,也不采用图形处理器加速。
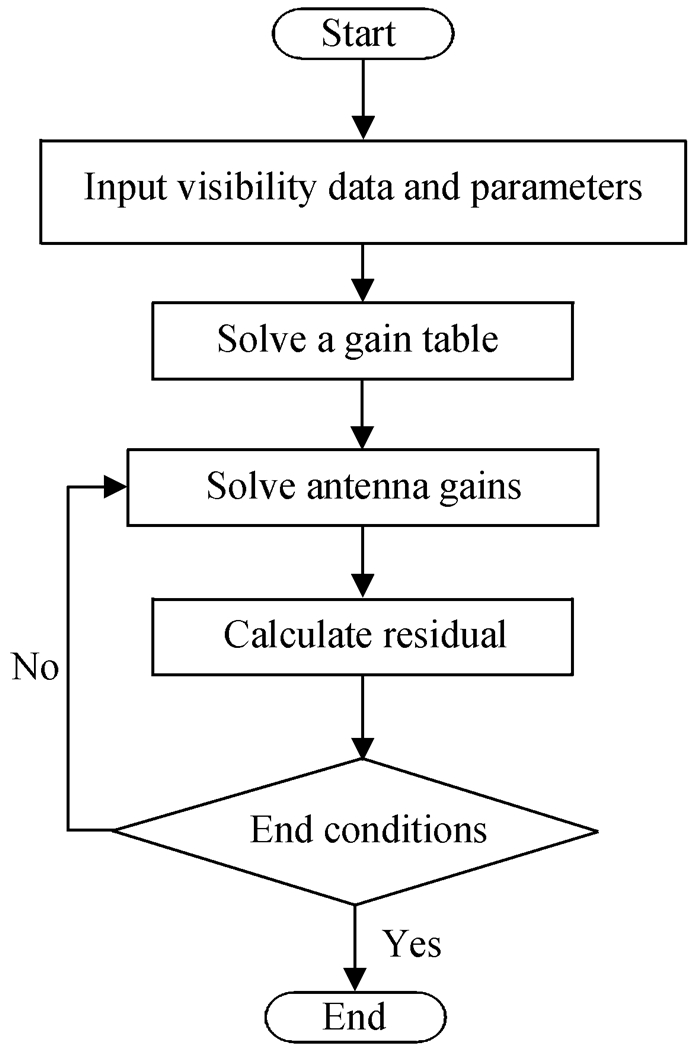
3.1 主要流程Antsol算法的实现流程如图 1,主要包括5个步骤:(1)输入可见度数据以及各种参数,包括观测可见度、模型可见度、迭代次数、容差等;(2)对观测可见度和模型可见度进行拟合,求解增益表;(3)求解单个天线的增益;(4)计算残差;(5)收敛条件检测,当达到迭代次数或者前后两次求解的增益变化小于预设值时,结束计算。
|
| 图 1 Antsol算法实现流程图 Fig. 1 The flow chart of the antsol algorithm implementation |
主要的函数见表 1,其中函数1用来求解增益表(包含增益、权重、残差等数据变量);函数2到4用来迭代求解不同极化数下所有天线的增益;函数5到7用来更新天线增益,分别被函数2、3、4调用;函数8和9用来求解残差,分别被函数5和函数7调用。
| No. | Function name | Desctiption |
| 1 | solve_gaintable | Solve a gain table by fitting an observed visibility to a model visibility |
| 2 | solve_antenna_gains_itsubs_scalar | Solve the antenna gains, x(antenna2, antenna1)=gain(antenna1) conj(gain(antenna2)) |
| 3 | solve_antenna_gains_itsubs_matrix | Solve the antenna gains using full matrix expressions |
| 4 | solve_antenna_gains_itsubs_vector | Solve the antenna gains using full vector expressions |
| 5 | gain_substitution_matrix | Gain calculation subfunction(matrix expressions), called by function 2 |
| 6 | gain_substitution_scalar | Gain calculation subfunction(scalar expressions), called by function 3 |
| 7 | gain_substitution_vector | Gain calculation subfunction(vector expressions), called by function 4 |
| 8 | Solution_residual_matrix | Calculate residual across all baselines of gain for point source equivalent visibilities, the results are expressed in matrix form, called by function 5 |
| 9 | Solution_residual_vector | Calculate the gain residual of a point source equivalent visibilities for all baselines, the results are expressed in vector form, called by function 7 |
参考甚大阵的Fortran程序,我们用Python语言实现了整个算法。以残值计算的函数solution_resudial_matrix为例,图 2给出了用基本的Python语言实现的残值计算流程,用了5重循环实现多天线的多通道计算,最后返回残值,参数gain表示增益数组,x表示点源等效可见度数组, xwt表示等效点源可见度权重数组。

|
| 图 2 残值计算函数solution_resudial_matrix() Fig. 2 Python code for the solution_resudial_matrix() |
显然,图 2的代码执行效率并不高。开发环境PyCharm中的Profile显示,图 2中的第7行到第16行的5重循环耗时最长,其次是第17行、18行的花式索引也消耗了大量时间。
4.1 代码优化经过多次尝试,本文最终采用Numpy的爱因斯坦求和约定(Einstein Summation Convention)对这段5重循环代码进行优化。爱因斯坦求和约定又称爱因斯坦标记法,是大科学家爱因斯坦于1916年提出的一种标记约定,Numpy, PyTorch, TensorFlow都实现了该标记法,相应的函数名称为einsum()。einsum()函数能快速灵活地实现矩阵计算,如矩阵转置、矩阵乘法、求迹、张量乘法、数组求和等。针对第17行、18行的花式索引,我们使用Numpy的putmask()函数实现数组的部分替换。图 3为最终的代码,可以看出,代码变得更为简洁优雅。

|
| 图 3 改进的残值计算函数solution_residual_matrix() Fig. 3 Optimized code for the solution_residual_matrix() |
我们使用RASCIL对SKA1-LOW进行了模拟观测,然后对所实现的Antsol算法的性能进行了测试。测试服务器环境为CentOS 7.8操作系统,Intel E5 2620 V4 CPU,128 G内存。表 2列出了优化前后几个主要函数的运行时间,可以看出,优化以后的程序执行时间大幅度缩短,其中残值矩阵计算函数Solution_residual_matrix()的计算时间约为之前的0.40%,而最快的残值矢量计算函数Solution_residual_vector()只有之前的0.20%。这是因为在用Python实现Antsol算法的过程中,在确保结果正确的同时,调用了Numpy的einsum()函数和putmask()函数,而Numpy是基于C/C++实现,因此程序的运行效率得到了大幅提升。
| No. | Function name | Execution time of the original code/ms | Execution time of the optimized code/ms | Ratio/% |
| 1 | gain_substitution_matrix | 12 630 | 121 | ~0.95 |
| 2 | gain_substitution_scalar | 947 | 66 | ~6.97 |
| 3 | gain_substitution_vector | 18 083 | 489 | ~2.70 |
| 4 | Solution_residual_matrix | 5 940 | 24 | ~0.40 |
| 5 | Solution_residual_vector | 11 433 | 23 | ~0.20 |
本文分析了天线增益校准算法Antsol的基本原理,并利用Numpy的爱因斯坦求和约定函数对Antsol算法进行了高性能实现,所实现的Antsol算法满足平方公里阵列数据处理软件RASCIL的性能要求,并已经集成到RASCIL中(https://gitlab.com/ska-telescope/external/rascil/-/blob/master/rascil/processing_components/calibration/solvers.py),不仅为当前平方公里阵列数据处理提供了支撑,也为未来数据处理的性能优化提供了算法参考。
| [1] |
窦玉江, DaleGary, 颜毅华, 等. 关于单天线跟踪指向校准和双天线基线校准的探讨[J]. 天文研究与技术-国家天文台台刊, 2009, 6(3): 202–208 DOU Y J, GARY D, YAN Y H, et al. Search of the methods for calibrating the single-antenna tracking/pointing and baselines of pairs of antennas[J]. Astronomical Research & Technology-Publications of National Astronomical Observatories of China, 2009, 6(3): 202–208. |
| [2] |
袁晓伟, 董亮, 汪敏, 等. 地网对VHF天线性能影响的分析研究[J]. 天文研究与技术, 2019, 16(2): 178–186 YUAN X W, DONG L, WANG M, et al. Simulation of the influence of ground screen parameters on antenna radiation performance in VHF band[J]. Astronomical Research & Technology, 2019, 16(2): 178–186. |
| [3] | BAGRI D S, THOMPSON A R. Hardware considerations for high-dynamic-range imaging[C]//Proceedings of the International Astronomical Union Colloquium. 1991, 131: 47-54. |
| [4] | CARILL C L, RAWLINGS S. Motivation, key science projects, standards and assumptions[J]. New Astronomy Reviews, 2004, 48(11): 979–984. |
| [5] | THOMPSON A, D'ADDARIO L. Frequency response of a synthesis array: performance limitations and design tolerances[J]. Radio Science, 1982, 17(2): 357–369. DOI: 10.1029/RS017i002p00357 |
| [6] | BHATNAGAR S. Computation of antenna dependent complex gains[R/OL]. 1998[2020-07-19]. http://www.aoc.nrao.edu/~sbhatnag/GMRT_Offline/antsol/antsol.html. |
| [7] | SCHWAB F R. Robust solution for antenna gains[R/OL]. 1982[2020-07-19]. https://library.nrao.edu/public/memos/vla/sci/legacy/memo136.pdf. |
| [8] | BOONSTRA A J, VAN DER VEEN A J. Gain calibration methods for radio telescope arrays[J]. IEEE Transactions on Signal Processing, 2003, 51(1): 25–38. DOI: 10.1109/TSP.2002.806588 |
| [9] | SALVINI S, WIJNHOLDS S J. StEFCal-an Alternating Direction Implicit method for fast full polarization array calibration[C]//Proceedings of the URSI General Assembly and Scientific Symposium. 2014: 1-4. |



