2. 中国科学院射电天文重点实验室, 江苏 南京 210008;
3. 国家天文科学数据中心, 北京 100101
2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210008, China;
3. National Astronomical Data Center, Beijing 100101, China
宇宙空间中的星际介质(Inter-Stellar Medium, ISM)[1]包含大量电离气体云、中性尘埃粒子和自由电子等物质。脉冲星信号在宇宙空间传播时因为星际介质色散的影响而降低速度,高频无线电波传播速度比低频快,所以高频和低频电磁波到达射电望远镜的时间不一致,脉冲星信号因此出现能量分散而使脉冲轮廓加宽,信噪比下降,甚至脉冲信号消失。
为了解决脉冲星信号色散问题,天文学家研究了消除色散的方法[2-3]及高速消色散处理技术。利用多通道滤波器组[4]对脉冲星信号进行通道划分,生成多个窄带信号,针对窄带信号进行时间延迟处理,每个通道延迟时间可以通过色散公式计算,最后将所有窄带通道累加,获得高信噪比的脉冲信号。
非相干消色散是脉冲星观测数据处理中最常用的色散处理方法,具有实现简单、速度快、数据后期处理灵活等优势。在脉冲星搜寻中,随着色散量(Dispersion Measure, DM)、数据通道及采样数量的增加,非相干消色散算法的计算量迅速增加,通常的计算平台难以实现脉冲星数据的实时处理。近年来,图形处理器[5-6]的可编程能力及并行处理能力迅速提高,应用范围不断扩展,在中央处理器+图形处理器混合计算系统中,图形处理器的加入大大提高了整个系统的数据处理能力。高性能图形处理器集群可提供强大的计算资源,能够满足海量天文数据实时处理的需求,从而解决脉冲星消色散算法计算量巨大、无法实时处理的问题。
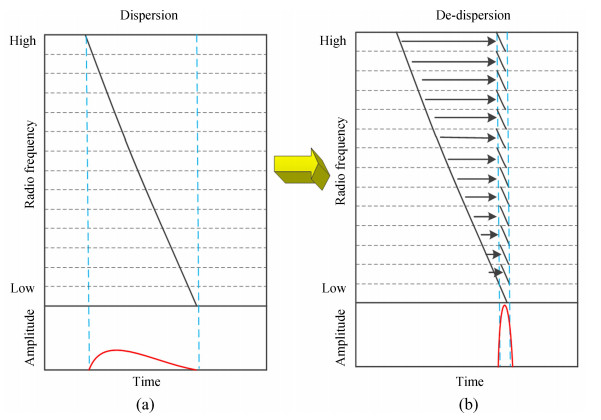
1 非相干消色散非相干消色散算法根据色散公式计算每个通道的延迟时间,然后加上各个通道的延迟,并把所有通道叠加在一起,即可消除数据的色散影响。非相干消色散原理如图 1。
|
| 图 1 非相干消色散原理 Fig. 1 The principle of incoherent de-dispersion |
非相干消色散采用多通道滤波器组实现,消色散处理过程主要包括:(1)通道划分,使用滤波器组把观测的天文信号总带宽分成若干个相互独立的狭窄通道;(2)补充时间延迟,根据色散公式计算每个通道的时间延迟,按延迟进行通道平移,将各个窄带通道的脉冲信号在同一时刻对齐;(3)通道累加,将所有通道时间序列叠加在一起。
图 1说明了非相干消色散的处理过程。图 1(a)未进行消色散,图 1(b)是消色散处理后的结果。从图 1可以看出,消色散前,通道累加之后脉冲宽度被展宽,输出信号信噪比下降,消色散之后可以得到信噪比大幅提高的脉冲星轮廓。
非相干消色散已经广泛应用于脉冲星、快速射电爆[7]搜寻。非相干消色散方法处理后的脉冲星数据,各个子通道内的色散延迟依旧存在,不能得到脉冲星的真实轮廓,随着频谱通道数的增加,每个通道的带宽变小,带内的色散效应相应降低,低频信号f1和高频信号f2在星际介质中的传播时间差为
| $ {t_2} - {t_1} = \frac{{{e^2}}}{{2{\rm{ \mathsf{ π} }}\mathit{cm}}}D\left( {\frac{1}{{f_1^2}} - \frac{1}{{f_2^2}}} \right), $ | (1) |
其中,c为光在真空中的传播速度;e为电子电荷;D为色散量;m为电子质量。D可表示为
| $ D = \int_0^d {{n_{\rm{e}}}{\rm{d}}l} \approx {n_{\rm{e}}}\mathit{d, } $ | (2) |
其中,ne为电子密度;d为电磁波实际经过的路径。
脉冲星消色散处理中,一个频率通道fchan相对于参考通道fref(通常是观测带宽中心频率)的时间延迟可以根据色散量公式计算:
| $ \Delta t = {K_{{\rm{DM}}}}D\left( {\frac{1}{{{f_{{\rm{ref}}}}^2}} - \frac{1}{{{f_{{\rm{chan}}}}^2}}} \right), $ | (3) |
其中,KDM为色散量常数;D为观测脉冲星信号的色散量,单位为cm-3·pc;频率单位为MHz。色散量常数为
| $ {K_{{\rm{DM}}}} = \frac{{{e^2}}}{{2{\rm{ \mathsf{ π} }}\mathit{cm}}} = 4.148808 \times {10^3}{\rm{MH}}{{\rm{z}}^{\rm{2}}} \cdot {\rm{p}}{{\rm{c}}^{{\rm{ - 1}}}} \cdot {\rm{c}}{{\rm{m}}^3} \cdot {\rm{s}}{\rm{.}} $ | (4) |
在观测中,观测频率f往往远大于划分的通道带宽Δf,如果f≫Δf时,频率通道的延迟时间可以写为
| $ {\mathit{t}_{{\rm{DM}}}} = 8.3 \times {10^6}D\Delta f{f^{ - 3}}{\rm{ms}}, $ | (5) |
(5) 式说明通道带宽和色散延迟时间成正比,为了得到更小的色散延迟,需要划分很细的窄带通道,尽量减小单通道信号带宽。
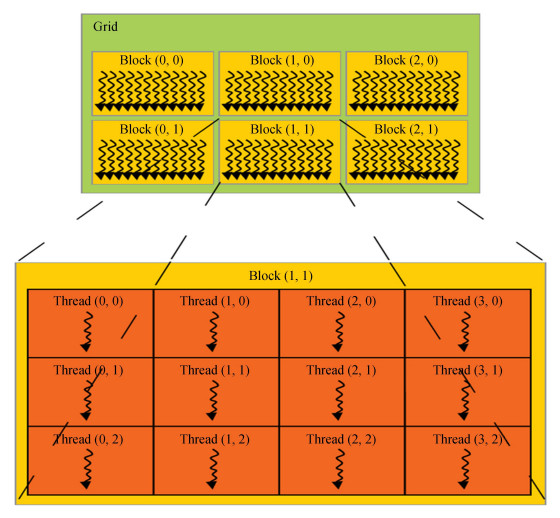
2 非相干消色散算法的图形处理器实现图形处理器是现代计算机中常见的设备,专为执行复杂的数学计算而设计的一种高度并行化、多线程的多核处理器,可以高速实现图形渲染。基于图形处理器的通用计算技术已经成为高性能并行计算领域的研究热点。图形处理器由于具备多个核心,更适合计算密集型数据。图形处理器的内核相当于中央处理器的多个线程,这些线程可以并行运行完成指定的计算任务,而且数值计算的速度远远优于中央处理器。图形处理器的线程结构如图 2。
|
| 图 2 图形处理器的线程结构 Fig. 2 GPU thread structure |
图形处理器的开发使用统一计算设备架构(Compute Unified Device Architecture, CUDA)[8],它是一种由英伟达(NVIDIA)推出的通用并行计算平台和编程模型,使图形处理器能够解决复杂的计算问题。CUDA提供了硬件的直接访问接口,不依赖图形应用程序接口实现图形处理器访问,在架构上采用全新的计算体系结构来使用图形处理器提供的硬件资源。CUDA采用标准C语言的扩展作为编程语言提供大量的高性能计算指令,能够在图形处理器强大的计算能力基础上实现效率更高的密集数据计算算法。
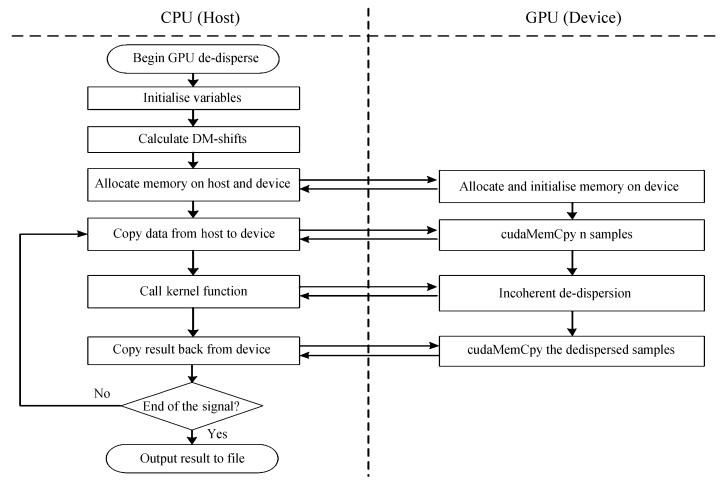
本文分析和研究非相干消色散算法的结构,把计算量大的任务部分映射到图形处理器的多线程进行处理。非相干消色散算法复杂度为O(NdNsNc),其中,Nd为色散量总数;Nc为通道数;Ns为采样数,算法数学模型计算量较大,但是通过图形处理器可以得到很高的加速比。在算法中,对非相干消色散的色散量和时间维度进行并行化,频率通道累加采用串行的处理方法,即使用图形处理器的单线程实现了Nc个通道的相加计算。在整个消色散过程中,中央处理器负责系统的初始化和输入数据读取,图形处理器负责并行消色散处理,中央处理器接收消色散后的时间序列并输出到数据文件。非相干消色散算法CUDA程序流程图如图 3。
|
| 图 3 非相干消色散CUDA程序流程图 Fig. 3 Flow chart of CUDA program for incoherent de-dispersion |
首先在中央处理器内存中开辟缓冲区,写入需要处理的数据。缓冲区暂存的采样都存在一定的色散,因此,需要对各个频率通道进行位移和累加运算,随着时间延迟增大,通道位移也增大,低频通道的位移量更大。为了减小中央处理器和图形处理器之间频繁的数据传输对算法计算性能的影响,在图形处理器中设置全局内存缓冲区,尽量把大量数据一次性复制过去,并且为写入和读取数据保留足够的存储空间。图形处理器kernel函数执行过程中,使用共享内存减小全局内存的延迟,提高运行速度。
为了提高算法的并行化加速,将非相干消色散算法的计算分为两部分,在中央处理器上执行计算的第1部分所需的时间
| $ {\mathit{t}_{{\rm{chan}}}} = 4.15 \times {10^3}\left( {f_1^{ - 2} - f_2^{ - 2}} \right), $ | (6) |
其中,f1,f2的单位为MHz;tchan的计算与色散量无关,使用图形处理器的常量内存存储。在图形处理器上执行计算的第2部分所需的时间
| $ {\mathit{t}_{{\rm{DM}}}} = \frac{{{\mathit{t}_{{\rm{chan}}}}D}}{{{\mathit{t}_{{\rm{samp}}}}}}, $ | (7) |
其中,tsamp为采样时间,单位为ms。
根据非相干消色散算法的特性,图形处理器kernel函数中定义了两个缓冲区:共享内存和常量内存,其中共享内存用于存储积分运算的结果,常量内存用于存储DM_shift。为了加快通道累加,使用共享内存隐藏全局内存的访问延迟。一个线程块里面的所有线程获取色散量平移值,并且存储到共享内存。对于每一个色散量,在共享内存中进行积分运算,并把消色散处理结果写入图形处理器的全局内存。
3 实验分析本次实验平台使用Intel Xeon E5-1620,TITAN V,CUDA 10.0及Ubuntu 18.04。TITAN V是一款NVIDIA GeForce系列高端图形处理器,拥有5120个CUDA核,内存访问带宽为652.8GB/s。
为了验证图形处理器并行算法的性能,首先分别模拟生成了32、64、128、256、512及1024通道脉冲星数据,其中心频率为420MHz,带宽为6MHz,采样间隔时间为165μs,脉冲星信号周期为0.1s,然后将每一块数据单独读取并加载到图形处理器中进行处理。实验结果如表 1、表 2、表 3及表 4。
| number of DM | 32 channel | 64 channel | 128 channel | |||||
| CPU | TITAN V | CPU | TITAN V | CPU | TITAN V | |||
| 1 | 0.0273 | 0.0078 | 0.0566 | 0.0148 | 0.1078 | 0.0289 | ||
| 2 | 0.0548 | 0.0085 | 0.1125 | 0.0154 | 0.2153 | 0.0296 | ||
| 5 | 0.1395 | 0.0102 | 0.2837 | 0.0172 | 0.5502 | 0.0324 | ||
| 10 | 0.2813 | 0.0132 | 0.5774 | 0.0204 | 1.1226 | 0.0357 | ||
| 20 | 0.5776 | 0.0189 | 1.2642 | 0.0265 | 2.3252 | 0.0434 | ||
| 40 | 1.4008 | 0.0314 | 2.7714 | 0.0393 | 5.3281 | 0.0599 | ||
| 80 | 3.0338 | 0.0574 | 6.0615 | 0.0658 | 11.9435 | 0.0962 | ||
| 160 | 6.1332 | 0.1193 | 13.0557 | 0.1273 | 26.7130 | 0.1636 | ||
| 320 | 13.8274 | 0.2556 | 29.5114 | 0.2740 | 56.2105 | 0.3399 | ||
| 640 | 33.9295 | 0.5106 | 65.7593 | 0.6378 | 134.9701 | 0.7307 | ||
| 1280 | 75.4416 | 1.0504 | 154.0248 | 1.3330 | 312.0603 | 1.7597 | ||
| 2560 | 158.7455 | 2.2094 | 329.0613 | 2.8760 | 668.0033 | 4.0038 | ||
| 5120 | 322.9089 | 4.3976 | 698.3460 | 6.0016 | 1389.3232 | 8.6268 | ||
| number of DM | 256 channel | 512 channel | 1024 channel | |||||
| CPU | TITAN V | CPU | TITAN V | CPU | TITAN V | |||
| 1 | 0.2103 | 0.0565 | 0.4204 | 0.1127 | 0.8289 | 0.2249 | ||
| 2 | 0.4308 | 0.0579 | 0.8371 | 0.1143 | 2.2732 | 0.2275 | ||
| 5 | 1.1644 | 0.0614 | 2.1853 | 0.1197 | 4.9677 | 0.2379 | ||
| 10 | 2.5279 | 0.0664 | 4.6357 | 0.1280 | 9.5110 | 0.2492 | ||
| 20 | 5.4891 | 0.0785 | 10.3499 | 0.1459 | 18.5704 | 0.2838 | ||
| 40 | 11.5288 | 0.1039 | 21.8757 | 0.1830 | 36.8282 | 0.3424 | ||
| 80 | 23.8050 | 0.1597 | 48.0757 | 0.2638 | 74.0204 | 0.4728 | ||
| 160 | 57.7672 | 0.2726 | 119.5114 | 0.4276 | 194.2584 | 0.7379 | ||
| 320 | 136.8641 | 0.5256 | 274.3375 | 0.7527 | 507.1785 | 1.2810 | ||
| 640 | 299.1812 | 1.0638 | 590.8383 | 1.4577 | 1161.6285 | 2.3831 | ||
| 1280 | 632.3722 | 2.5118 | 1238.2926 | 2.9597 | 2463.5231 | 4.6113 | ||
| 2560 | 1299.2245 | 6.8297 | 2592.5578 | 7.0263 | 5102.2142 | 9.3347 | ||
| 5120 | 2749.8164 | 19.221491 | 5533.0351 | 17.4777 | 10995.2138 | 20.4063 | ||
| number of DM |
4096 sample | 8192 sample | 16384 sample | 32768 sample | |||||||
| CPU | TITAN V | CPU | TITAN V | CPU | TITAN V | CPU | TITAN V | ||||
| 1 | 0.0259 | 0.0073 | 0.0519 | 0.0145 | 0.1037 | 0.0287 | 0.2072 | 0.0577 | |||
| 2 | 0.0518 | 0.0073 | 0.1036 | 0.0144 | 0.2075 | 0.0286 | 0.4147 | 0.0569 | |||
| 5 | 0.1307 | 0.0077 | 0.2624 | 0.0151 | 0.5251 | 0.0298 | 1.0499 | 0.0598 | |||
| 10 | 0.2656 | 0.0081 | 0.5379 | 0.0157 | 1.0764 | 0.0313 | 2.1585 | 0.0625 | |||
| 20 | 0.5430 | 0.0086 | 1.1102 | 0.0171 | 2.2238 | 0.0348 | 4.4429 | 0.0699 | |||
| 40 | 1.0930 | 0.0099 | 2.2470 | 0.0205 | 4.5026 | 0.0414 | 9.1970 | 0.0852 | |||
| 80 | 2.2684 | 0.0129 | 4.6959 | 0.0266 | 9.3686 | 0.0565 | 18.5134 | 0.1147 | |||
| 160 | 5.4016 | 0.0191 | 12.2362 | 0.0401 | 24.2389 | 0.0859 | 48.6114 | 0.1781 | |||
| 320 | 12.6597 | 0.0296 | 31.9656 | 0.0705 | 63.5571 | 0.1461 | 126.8976 | 0.3047 | |||
| 640 | 28.2764 | 0.0541 | 71.4992 | 0.1230 | 144.0788 | 0.2692 | 288.2967 | 0.5664 | |||
| 1280 | 61.5773 | 0.1020 | 150.4389 | 0.2408 | 299.1604 | 0.5263 | 614.7442 | 1.1099 | |||
| 2560 | 129.2098 | 0.2064 | 302.7521 | 0.4777 | 637.8879 | 1.0559 | 1280.9965 | 2.2027 | |||
| 5120 | 281.6858 | 0.4243 | 672.2270 | 0.9917 | 1374.9966 | 2.1815 | 2756.7142 | 4.5928 | |||
| Channel | Sample | 4096 | 8192 | 16384 | 32768 | 65536 |
| 32 | CPU | 7.4468 | 15.0353 | 30.2430 | 60.6416 | 133.7846 |
| TITAN V | 0.1002 | 0.2003 | 0.4215 | 0.8864 | 2.0978 | |
| 64 | CPU | 14.5728 | 29.8505 | 59.7925 | 123.8967 | 330.8217 |
| TITAN V | 0.1127 | 0.2164 | 0.4667 | 1.2664 | 2.8659 | |
| 128 | CPU | 28.6676 | 57.8297 | 118.1305 | 316.7424 | 703.6475 |
| TITAN V | 0.1307 | 0.2665 | 0.7702 | 1.9095 | 4.0631 | |
| 256 | CPU | 53.8793 | 111.2041 | 301.5122 | 694.0670 | 1386.7769 |
| TITAN V | 0.1519 | 0.4544 | 1.1833 | 3.4037 | 8.927236 | |
| 512 | CPU | 104.1580 | 282.3113 | 684.1435 | 1361.1676 | 2718.7850 |
| TITAN V | 0.2411 | 0.6064 | 1.4260 | 3.3107 | 7.3363 | |
| 1024 | CPU | 281.2189 | 684.9610 | 1375.0873 | 2744.7187 | 5494.2190 |
| TITAN V | 0.4230 | 1.0071 | 2.1739 | 4.6273 | 9.8898 |
表 1、表 2是在采样数为131072(单通道采样),通道和色散量都变化的情况下图形处理器并行算法和中央处理器串行算法的非相干消色散处理消耗时间。从表中可以看出,当通道数量固定时,随着色散量的增加,图形处理器和中央处理器的数据处理时间线性增加,图形处理器的消色散处理时间远远少于中央处理器的;当色散量固定时,随着数据通道数量的增加,中央处理器和图形处理器的处理时间增加,但是中央处理器的计算时间比图形处理器大得多。
表 3是通道数为1024、采样数和色散量都变化的情况下,图形处理器并行算法和中央处理器串行算法的非相干消色散处理消耗时间。当采样数固定时,随着色散量的增加,图形处理器和中央处理器的数据处理时间增加;当色散量固定时,随着采样数的增加,并行和串行算法处理时间增加,但是,图形处理器的计算时间少于中央处理器的,计算速度有几百倍的差距。从表中可以看出,图形处理器大大缩短了非相干消色散的执行时间。
表 4是色散量为5120、采样数和通道数都变化的情况下,图形处理器并行算法和中央处理器串行算法的非相干消色散处理消耗时间。当采样数固定时,随着通道数的增加,图形处理器和中央处理器的数据处理时间增加;当通道数固定时,随着采样数的增加,并行和串行算法处理时间增加。在通道数或采样数变化的情况下,图形处理器的运算时间均小于中央处理器,且消耗时间差距明显。
和中央处理器相比,图形处理器非相干消色散的数据处理能力达到几百倍的加速比,具有显著的加速优势。图形处理器并行算法的加速比性能如图 4、图 5及图 6。
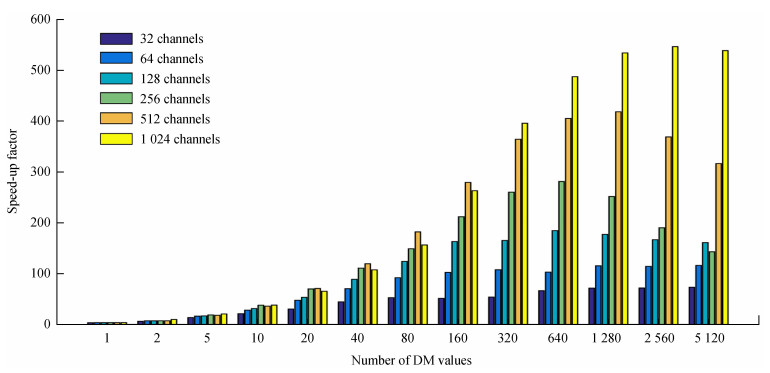
|
| 图 4 采样数为131072时图形处理器算法加速比 Fig. 4 GPU algorithm speed-up when the number of samples is 131072 |
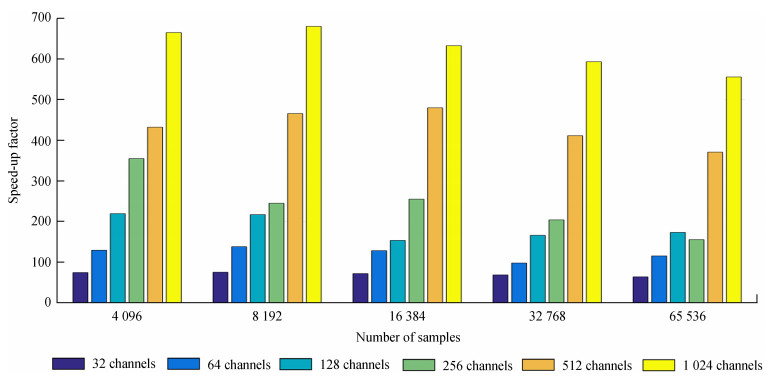
|
| 图 5 色散量为5120时图形处理器算法加速比 Fig. 5 GPU algorithm speed-up when the number of DMs is 5120 |
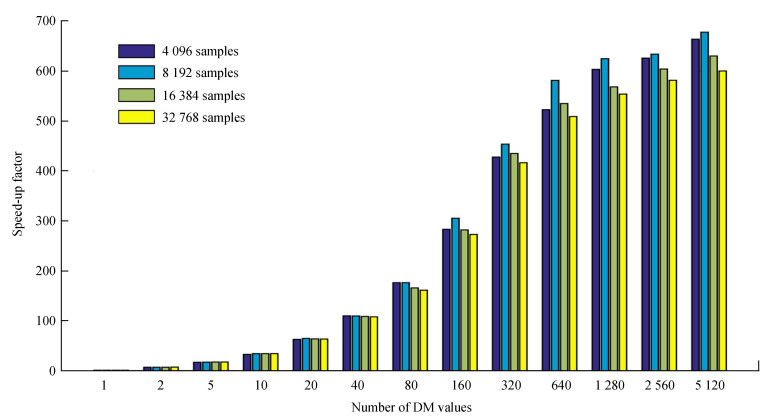
|
| 图 6 通道数为1024时图形处理器算法加速比 Fig. 6 GPU algorithm speed-up when the number of channels is 131072 |
图 4是采样数为131072、通道数和色散量均变化的情况下,图形处理器并行算法的加速比。从图中可以看出,随着色散量的增加,并行算法的加速比提高。当色散量个数为2560时,TITAN V的加速比最高(即达到中央处理器速度的538倍),然后加速比开始下降。如图 4,通道数量越多,图形处理器算法的加速比越大,加速性能越好。当通道数为1024时加速比最高,当通道数为32时加速比最小。
图 5是色散量为5120、通道数和采样数都变化的情况下,图形处理器并行算法的加速比。从图中可以看出,随着采样数的增加,并行算法的加速比有所下降,但算法加速高达550多倍。当通道数为1024时,TITAN V达到最高的加速比。当通道数为1024、采样数为8192时,图形处理器并行算法的速度是中央处理器串行算法的780多倍。
图 6是通道数为1024、采样数和色散量都变化的情况下,图形处理器并行算法的加速比。从图中可以看出,色散量个数对图形处理器非相干消色散算法加速比影响最大。随着色散量的增加,图形处理器并行算法的加速比迅速提高。如图 6,色散量个数越大,计算消耗时间越多,当色散量为5120时加速比最大。
实验结果表明,采样数、通道数及色散量个数都是影响图形处理器算法加速性能的关键因素。非相干算法执行过程中,图形处理器展示了强大的并行化处理优势,节省了大量重复计算时间,提升了算法的计算效率。
4 总结本文研究基于图形处理器的非相干消色散算法,提出了相关算法的图形处理器并行化加速方案,分析了算法的密集型计算部分,研究了图形处理器多线程任务分配、管理及存器层次的优化方法,提高了图形处理器资源利用率,显著提升了算法的计算性能。在图形处理器算法的实现过程中,我们深入分析了影响并行算法性能的主要因素,优化了CUDA程序,大大减少了算法执行的时间,图形处理器消色散算法加速比接近700倍,解决了算法在中央处理器上计算量巨大、无法实时处理的问题,通过实验分析算法的数据处理时间和加速比,验证了并行算法性能。
| [1] | SPITZER L, J r. Physical processes in the interstellar medium[M]. New York: John Wiley & Sons, 2008. |
| [2] | BARSDELL B R, BAILES M, BARNES D G, et al. Accelerating incoherent dedispersion[J]. Monthly Notices of the Royal Astronomical Society, 2012, 422(1): 379–392. DOI: 10.1111/j.1365-2966.2012.20622.x |
| [3] |
黄玉祥, 汪敏, 郝龙飞, 等. 脉冲星信号相干消色散与非相干消色散的比较研究[J]. 天文研究与技术, 2019, 16(1): 16–24 HUANG Y X, WANG M, HAO L F, et al. Comparative study between the coherent de-dispersion and the incoherent de-dispersion of pulsar signal[J]. Astronomical Research & Technology, 2019, 16(1): 16–24. |
| [4] |
托乎提努尔, 张海龙, 王杰. 基于CUDA的射电天文多相滤波器组设计[J]. 天文研究与技术, 2017, 14(1): 117–123 TOHTONUR, ZHANG H L, WANG J. A design of polyphasefilter bank for radio astronomy based on CUDA[J]. Astronomical Research & Technology, 2017, 14(1): 117–123. |
| [5] |
苏统华, 李东, 李松泽. CUDA并行程序设计:GPU编程指南[M]. 北京: 机械工业出版社, 2014. SU T H, LI D, LI S Z. CUDA programming:adeveloper's guide to parallel computing with GPU[M]. Beijing: China Machine Press, 2014. |
| [6] |
FARBERR. 高性能CUDA应用设计与开发[M]. 北京: 机械工业出版社, 2013. FARBER R. CUDA application design and development[M]. Beijing: China Machine Press, 2013. |
| [7] | PETROFF E, OOSTRUM L C, STAPPERS B W, et al. A fast radio burst with a low dispersion measure[J]. Monthly Notices of the Royal Astronomical Society, 2019, 482(3): 3109–3115. |
| [8] | CHENG J, GROSSMAN M, MCKERCHER T. Professional CUDA C programming[M]. New York: John Wiley & Sons, 2014. |



