伽玛射线暴(伽玛暴)是最近几十年来观测到的最剧烈的天文现象之一,它具有光度高、能量高和持续时间短等特点。伽玛暴产生的机制、光谱的形成及形状仍然不清楚,它的辐射机制是目前的研究热点之一。伽玛暴谱由热辐射成分和非热辐射成分组成,热辐射来自于火球光球层,可以用火球模型预测,在一些伽玛暴中能够发现热成分的存在[1-2]。望远镜观测到的非热辐射谱是简单的拐折幂率谱,最可能产生非热谱的机制是同步辐射和逆康普顿散射,目前的多波段观测不支持逆康普顿散射机制[3],所以在产生伽玛暴的机制中同步辐射是一个较好的候选者,并且它可以在标准火球模型中产生。在标准火球模型中,伽玛暴中心引擎发射许多以相对论速度运动的壳层,当速度较快的壳层追赶上速度较慢的壳层时,壳层发生碰撞形成激波,激波中的电子被加速后在辐射区磁场中高速旋转,高能伽玛光子通过同步辐射机制发射[4-5](内激波模型)。如果火球壳层磁化率σ>1,壳层碰撞使辐射源周围磁场磁感线发生重联,电子在新的磁场中被加速(磁重联模型[6-7])。内激波和磁重联模型是伽玛暴瞬时辐射的两种主流模型。
在观测上,一个经验的双幂率光滑连接函数(波段函数)能够拟合大部分亮暴[8],两段幂率分别由低能量和高能量光子指数α和β描述。幂率高能截断的康普顿模型(Cutoff Plow Law, CPL)能够拟合一些暗暴,当波段函数的高能指数趋近无穷时,即β→∞,波段函数转变为单幂率高能截断的康普顿模型函数。另外,平滑拐折幂率模型能够拟合一些亮暴[9],除了高低能谱指数α和β外,还引入了一个描述光谱拐折锐度的量Δ,并且平滑拐折幂率模型的谱拐折随Δ的增大而变得越来越平滑[10],对于费米监测器(Fermi Gamma-ray Space Telescope/Gamma-ray Burst Monitor, Fermi/GBM)数据Δ的值固定在0.3。但是,文[9]使用上述3个模型拟合81个亮暴的时间分辨数据,得到大部分能谱的最佳拟合模型是单幂率高能截断的康普顿模型。此外,文[11-12]利用谱宽度W和谱锐度角度θ测试同步模型解释伽玛暴谱的能力,发现伽玛暴谱比同步辐射谱更窄更尖,这表明伽玛暴谱的谱拐折更加尖锐。为了对伽玛暴谱的形状进一步研究,尤其是能谱峰和拐折附近谱的形状,本文使用平滑拐折幂率模型、折线幂率模型和波段函数模型拟合8个费米亮暴的时间分辨谱。然后根据模型拟合优度在所有的能谱中找出最佳拟合谱,最后得到每个能谱的时间积分能流,可以从能流的角度得到3个模型的最佳拟合范围以及伽玛暴能谱峰或谱拐折附近的谱形状。
1 样本选取和分析方法费米监测器由12个碘化钠(NaI,覆盖能量范围8~900keV)探测器和2个锗酸铋(Bismuth Germanium Oxide, BGO,覆盖能量范围200keV~40MeV)探测器组成,覆盖的能量范围为8keV~40MeV[13]。在光谱分析时,每个暴一般选择3个辐射脉冲信号最强的探测器,首先确定2个最亮的NaI探测器,另外1个BGO探测器也随之确定。费米监测器观测数据保存为3种文件类型:CTIME文件、CSPEC文件和TTE文件,相比前两种文件类型,TTE文件有最小的时间分辨率(2μs),因此,本文使用TTE数据进行时间分辨谱分析。根据伽玛暴在整个瞬时辐射过程中能量流量Fe≥4×10-5erg·s-1·cm-2或光子流量Fp≥20ph·s-1·cm-2 [9],选择几个最亮的长暴如表 1,并且使用一个新的光谱拟合包完成光谱分析,该包是基于马尔可夫链蒙特卡尔理论(Markov Chain Monte Carlo, MCMC),文[14]对这个光谱拟合包进行了详细描述。
| GRBs | T90/s | Detector | Fe/(erg•s-1•cm-2) | Fp(64\\256\\1024)/(ph•s-1•cm-2) | ||
| 140329 | 21.248 | n8 nb b1 | 6.70E-05±3.32E-08 | 128.261±3.9240 | 116.233±1.9083 | 104.63±0.9108 |
| 101123 | 103.938 | n9 na b1 | 1.17E-04±5.29E-08 | 50.4388±2.1025 | 45.5368±1.0179 | 39.4933±0.4845 |
| 100826 | 84.993 | n7 n8 b1 | 1.64E-04±9.71E-08 | 37.3346±1.7127 | 33.1921±0.8096 | 29.5819±0.3972 |
| 130427 | 138.242 | n9 na b1 | 2.46E-03±1.24E-06 | 1259.22±10.5135 | 1210.15±4.8497 | 1051.86±2.2150 |
| 170114 | 12.032 | n1 n2 b0 | 1.82E-05±6.18E-08 | 32.2350±1.9843 | 29.7231±0.9272 | 26.6774±0.4500 |
| 171010 | 107.266 | n8 nb b1 | 6.33E-04±9.85E-08 | 137.251±4.4113 | 133.092±2.1779 | 120.14±1.0478 |
| 150627 | 64.577 | n3 n4 b0 | 1.80E-04±3.83E-07 | 78.4556±2.5316 | 75.7634±1.2617 | 65.2531±0.5985 |
| 180720 | 48.897 | n6 n7 b1 | 2.99E-04±9.03E-08 | 170.578±2.6555 | 158.29±1.2936 | 124.548±0.5908 |
经验的波段函数模型定义为[8]
| $ {f_{{\rm{Band}}}}\left( E \right) = A\left\{ {\begin{array}{*{20}{l}} {{{\left( {\frac{E}{{100{\rm{keV}}}}} \right)}^\alpha }{\rm{exp}}\left[ { - \frac{{\left( {\alpha + 2} \right)E}}{{{E_p}}}} \right]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E < {E_c}}\\ {{{\left( {\frac{E}{{100{\rm{keV}}}}} \right)}^\alpha }{\rm{exp}}\left( {\beta - \alpha } \right){{\left( {\frac{{{E_c}}}{{100{\rm{keV}}}}} \right)}^{\alpha - \beta }}\;\;\;\;\;E \ge {E_c}} \end{array},} \right. $ | (1) |
其中,
平滑拐折幂率模型定义为[15]
| $ {f_{{\rm{SBPL}}}}\left( E \right) = {N_0}{\left[ {{{\left( {\frac{E}{{{E_{\rm{b}}}}}} \right)}^{w\alpha }} + {{\left( {\frac{E}{{{E_{\rm{b}}}}}} \right)}^{w\beta }}} \right]^{ - 1/w}} \cdot $ | (2) |
折线幂率模型定义为
| $ {f_{{\rm{BPL}}}}\left( E \right) = {N_0}\left\{ {\begin{array}{*{20}{c}} {{{\left( {\frac{E}{{{E_{\rm{b}}}}}} \right)}^{ - \alpha }}}&{E < {E_b}}\\ {{{\left( {\frac{E}{{{E_{\rm{b}}}}}} \right)}^{ - \beta }}}&{E \ge {E_b}} \end{array}} \right. \cdot $ | (3) |
在(2)式和(3)式中,N0为能量在100keV时的归一化常数,单位为ph·s-1·cm-2·keV-1;Eb为νFν能谱拐折处的能量,单位为keV;α和β分别为低能段和高能段幂律谱指数;w为描述光谱拐折锐度的拐折尺度。
2 分析结果使用波段函数模型、平滑拐折幂率模型和折线幂率模型分别拟合8个暴的时间分辨谱,其中,两个暴的部分拟合结果如表 2,表中第1列为伽玛暴名字;第2列为光谱分析的开始和结束时间;第3列为拟合模型;第4~8列为模型拟合参数;第9列为χ2/Dof;第10列为贝叶斯信息准则(Bayesian Information Criteria, BIC,定义为BIC=χ2+n_params×ln(n_datapoints),n_params是拟合模型参数,n_datapoints是数据点个数;贝叶斯公式对发生概率进行修正,再利用期望值和修正概率做出最优决策,对同一组数据拟合中,BIC越小的模型优度越好);第11列为能流(1~104keV)。3个模型拟合8个暴的165个时间分辨谱,得到495个拟合能谱。在能流比较小的伽玛暴中,从3个模型的BIC值可以粗略得到折线幂率模型比平滑拐折幂率模型和波段函数模型有更好的拟合结果,而在能量能流比较大的伽玛暴中,波段函数模型和平滑拐折幂率模型的拟合优于折线幂率模型。
| GRBs | Tstart: Tend | Models | logA/N0 | α | Ep/Eb(keV) | β | w | χ2/Dof | BIC | Fluence(10-5 erg•cm-2) |
| 100826 | 13.75:14.50 | Band | -1.39+0.01 -0.01 | -1.10-0.01+0.02 | 5604.98-512.81+468.27 | -4.33-5.63+1.55 | - | 518.78/348 | 542.24 | 2.21-0.19+0.23 |
| SBPL | -2.94+0.04 -0.05 | 1.16-0.02+0.01 | 3189.88-203.51+260.72 | 3.37-2.21+0.23 | 25.23-11.15+18.3 | 458.08/359 | 487.47 | 2.04-0.01+0.03 | ||
| BPL | -3.11-0.05+0.04 | 1.12-0.01+0.01 | 3354.73-167.95+312.55 | 3.83-0.32+0.75 | - | 457.98/360 | 481.57 | 2.01-0.02+0.03 | ||
| 14.50:15.25 | Band | -1.37-0.01+0.01 | -1.10-0.02+0.02 | 5905.59-263.90+869.68 | -4.13-5.99+1.76 | - | 565.57/348 | 589.02 | 2.37-0.19+0.16 | |
| SBPL | -2.90-0.05+0.04 | 3.55-2.40+0.42 | 3089.00-91.47+382.11 | 1.15-0.02+2.77 | 41.79-28.68+1.28 | 489.21/359 | 518.69 | 2.24-0.01+0.03 | ||
| BPL | -3.16-0.05+0.04 | 1.12-0.02+0.01 | 3829.53-186.49+361.64 | 4.40-0.47+1.17 | - | 489.01/360 | 512.60 | 2.23-0.01+0.01 | ||
| 15.25:16.00 | Band | -1.40-0.01+0.01 | -1.12-0.02+0.02 | 6147.79-62350+689.86 | -2.62-6.44+0.52 | - | 513.68/348 | 537.13 | 2.31-0.14+0.20 | |
| SBPL | -2.98-0.04+0.04 | 1.17-0.02+0.01 | 3575.88206.22+209.05 | 5.28-4.10+1.06 | 31.53-19.78+11.34 | 415.07/359 | 444.55 | 2.28-0.01+0.03 | ||
| BPL | -3.16-0.07+0.02 | 1.12-0.00+0.02 | 3695.96-134.59+417.65 | 5.10-0.49+2.10 | - | 415.03/360 | 438.62 | 2.29-0.52+0.33 | ||
| 16.00:16.75 | Band | -1.40-0.01+0.01 | -1.13-0.03+0.01 | 6214.13-517.62+861.62 | -3.31-6.18+1.10 | - | 556.78/348 | 537.13 | 2.53-0.19+0.65 | |
| SBPL | -2.82-0.02+0.03 | 3.52-2.38+0.28 | 2878.97-105.01+211.06 | 1.15-0.01+2.65 | 49.09-14.35+0.90 | 474.72/359 | 504.21 | 2.28-0.01+0.03 | ||
| BPL | -3.22-0.06+0.03 | 1.14-0.01+0.02 | 3888.17-215.44+367.65 | 6.12-1.17+2.83 | - | 474.58/360 | 498.17 | 2.28-0.01+0.05 | ||
| 16.75:17.50 | Band | -1.38-0.01+0.01 | -1.12-0.02+0.01 | 6090.86-531.91+701.64 | -5.63-5.64+3.13 | - | 471.55/348 | 495.00 | 2.90-0.16+0.23 | |
| SBPL | -2.81-0.03+0.04 | 1.17-0.01+2.40 | 2813.19-182.34+292.75 | 3.39-2.22+0.21 | 9.73-8.40+16.07 | 434.55/359 | 464.04 | 2.81-0.01+0.03 | ||
| BPL | -3.27-0.02+0.04 | 1.14-0.01+0.02 | 4552.39-324.23+71.17 | 9.26-3.21+0.11 | - | 434.69/360 | 458.28 | 2.86-0.01+0.01 | ||
| 17.50:18.25 | Band | -1.41-0.01+0.01 | -1.12-0.03+0.01 | 5908.59-37.86+1532.74 | -2.52-6.93+0.48 | - | 552.28/348 | 575.74 | 2.75-0.21+0.26 | |
| SBPL | -2.92-0.03+0.02 | 1.17-0.03+0.01 | 3305.28-143.79+221.04 | 4.11-2.93+0.40 | 33.95-19.14+9.76 | 491.91/359 | 520.72 | 2.64-0.01+0.03 | ||
| BPL | -3.19-0.06+0.03 | 1.13-0.01+0.02 | 3686.78-137.67+356.70 | 5.54-0.74+2.94 | - | 491.02/360 | 514.61 | 2.66-0.03+0.03 | ||
| 18.25:19.00 | Band | -1.41-0.01+0.01 | -1.14-0.02+0.02 | 6824.58-468.78+1125.88 | -2.88-6.32+0.67 | - | 541.80/348 | 565.26 | 2.63-0.18+0.18 | |
| SBPL | -2.78-0.03+0.03 | 1.16-0.03+0.01 | 3014.88-154.25+263.99 | 3.82-2.67+0.34 | 18.72-8.29+23.62 | 496.91/359 | 526.40 | 2.46-0.01+0.03 | ||
| BPL | -3.18-0.05+0.03 | 1.12-0.01+0.02 | 3776.04-152.30+317.09 | 4.78-0.60+2.09 | - | 496.96/360 | 520.55 | 2.45-0.05+0.03 | ||
| 19.00:19.75 | Band | -1.40-0.01+0.01 | -1.14-0.01+0.02 | 6588.16-694.73+590.05 | -3.55-6.02+1.22 | - | 476.42/348 | 499.88 | 2.91-0.25+0.16 | |
| SBPL | -2.66-0.04+0.05 | 3.47-2.33+0.14 | 2661.68-235.16+194.73 | 1.15-1.43+0.01 | 9.97-8.88+16.09 | 453.50/359 | 482.99 | 2.68-0.01+0.03 | ||
| BPL | -3.18-0.06+0.03 | 1.14-0.02+0.01 | 3610.99-153.32+370.57 | 3.71-0.28+0.73 | - | 453.65/360 | 477.23 | 2.69-0.09+0.03 | ||
| 19.75:20.50 | Band | -1.36-0.01+0.01 | -1.08-0.02+0.02 | 5068.36-425.26+451.72 | -3.91-5.92+1.44 | - | 451.09/348 | 474.55 | 3.13-0.21+0.24 | |
| SBPL | -2.68-0.06+0.04 | 1.14-0.03+0.01 | 2662.30-178.55+288.95 | 3.121.98+0.23 | 6.49-5.06+16.88 | 423.93/359 | 453.41 | 3.13-0.01+0.03 | ||
| BPL | -3.12-0.05+0.03 | 1.11-0.02+0.01 | 3816.46-164.19+319.04 | 5.80-0.45+2.25 | - | 424.55/360 | 448.14 | 3.10-0.01+0.00 | ||
| 20.50:21.25 | Band | -1.32-0.01+0.01 | -1.07-0.01+0.02 | 5206.91-244.94+628.52 | -3.20-6.31+0.88 | - | 517.86/348 | 541.32 | 3.22-0.26+0.26 | |
| SBPL | -2.65-0.03+0.01 | 1.13-0.01+0.01 | 2678.51-193.21+159.97 | 3.87-2.75+0.21 | 22.85-12.71+5.06 | 478.32/359 | 507.81 | 3.19-0.03+0.03 | ||
| BPL | -3.00-0.05+0.02 | 1.10-0.00+0.02 | 3352.12-117.80+296.47 | 3.77-0.34+0.63 | - | 478.29/360 | 501.88 | 3.16-0.01+0.03 | ||
| 21.25:22.00 | Band | -1.30-0.01+0.01 | -1.11-0.01+0.02 | 5085.20-258.51+680.86 | -2.97-6.46+0.68 | - | 492.86/348 | 516.32 | 3.39-0.27+0.27 | |
| SBPL | -2.73-0.03+0.03 | 1.15-0.01+0.01 | 2852.85-140.63+228.06 | 3.64-2.49+0.26 | 22.82-11.44+20.42 | 445.72/359 | 475.20 | 3.39-0.04+0.03 | ||
| BPL | -3.06-0.05+0.02 | 1.13-0.01+0.01 | 3498.18-92.74+326.39 | 4.36-0.33+1.33 | - | 445.53/360 | 469.12 | 3.41-0.01+0.03 | ||
| 22.00:22.75 | Band | -1.30-0.01+0.01 | -1.11-0.02+0.01 | 4719.17-266.30+582.73 | -3.79-5.76+1.21 | - | 441.12/348 | 464.57 | 3.49-0.21+0.19 | |
| SBPL | -2.61-0.05+0.03 | 3.07-1.94+0.17 | 2531.36-117.33+225.97 | 1.13-0.01+2.12 | 41.81-29.59+1.49 | 418.73/359 | 448.22 | 3.41-0.51+0.03 | ||
| BPL | -3.08-0.05+0.02 | 1.13-0.01+0.01 | 3641.87-116.26+305.60 | 6.26-0.87+2.47 | - | 418.63/360 | 442.22 | 3.41-0.01+0.01 | ||
| 22.75:23.50 | Band | -1.28-0.01+0.01 | -1.09-0.02+0.01 | 4974.01-440.89+360.56 | -2.96-0.03+0.02 | - | 563.99/348 | 587.45 | 3.41-0.01+0.23 | |
| SBPL | -2.75-0.06+0.02 | 1.15-0.03+0.03 | 2856.13-120.96+279.52 | 3.36-2.21+0.28 | 43.66-14.83+2.67 | 492.06/359 | 521.55 | 3.45-0.01+0.05 | ||
| BPL | -3.11-0.01+0.05 | 1.12-0.01+0.01 | 4105.08-356.63+49.68 | 9.36-1.58+0.64 | - | 492.05/360 | 515.64 | 3.47-0.02+0.03 | ||
| 23.50:24.25 | Band | -1.21-0.01+0.01 | -1.12-0.02+0.01 | 4801.31-320.76+438.39 | -2.92-6.64+0.57 | - | 512.96/359 | 536.42 | 3.49-0.29+0.34 | |
| SBPL | -2.92-0.05+0.03 | 1.17-0.02+0.01 | 3430.48-164.19+319.04 | 3.98-0.45+2.55 | 47.29-14.91+2.67 | 448.58/359 | 478.07 | 3.55-0.04+0.05 | ||
| BPL | -2.94-0.05+0.03 | 1.16-0.01+0.01 | 3056.49-159.65+300.70 | 3.17-0.26+0.91 | - | 448.62/360 | 472.21 | 3.54-0.01+0.01 | ||
| 130427 | 0.00:0.78 | Band | -0.32-0.01+0.01 | -0.64-0.02+0.02 | 625.74-15.36+19.70 | -2.73-0.12+0.06 | - | 493.4/348 | 516.89 | 5.17-0.20+0.18 |
| SBPL | -0.99-0.00+0.04 | 0.63-0.01+0.01 | 1197.35-87.74+68.05 | 4.37-0.16+0.21 | 0.29-0.03+0.01 | 517.51/358 | 546.98 | 6.52-0.27+0.23 | ||
| BPL | -0.91-0.05+0.02 | 0.84-0.01+0.02 | 354.04-13.09+15.4 | 2.33-0.05+0.04 | - | 819.67/359 | 843.25 | 7.04-0.24+0.23 | ||
| 0.78:1.57 | Band | -0.17-0.02+0.03 | -0.63-0.03+0.04 | 191.02-9.78+7.17 | -2.25-0.04+0.04 | - | 411.90/348 | 435.39 | 2.08-0.01+0.13 | |
| SBPL | -0.17-0.06+0.03 | 2.38-1.65+0.04 | 101.57-0.54+17.71 | 0.58-0.03+0.84 | 0.92-0.11+0.15 | 445.84/358 | 475.31 | 2.59-0.19+0.03 | ||
| BPL | -0.46-0.05+0.02 | 0.93-0.01+0.01 | 108.89-3.41+4.46 | 2.12-0.33+1.33 | - | 520.52/359 | 544.10 | 2.87-0.01+0.13 | ||
| 1.57:2.35 | Band | 0.05-0.06+0.05 | -0.35-0.07+0.06 | 99.17-4.10+4.94 | -2.17-0.03+0.03 | - | 375.5/348 | 398.93 | 1.19-0.08+0.09 | |
| SBPL | -0.33-0.01+0.01 | 0.88-0.02+0.02 | 70.49-0.06+4.24 | 2.19-0.04+0.02 | 4.96-0.21+18.58 | 426.08/358 | 455.55 | 1.50-0.11+0.15 | ||
| BPL | -0.34-0.03+0.02 | 0.89-0.03+0.03 | 68.97-2.94+2.61 | 2.14-0.03+0.03 | - | 435.37/359 | 458.95 | 1.58-0.09+0.03 | ||
| 2.35:3.13 | Band | -0.10-0.11+0.08 | -0.46-0.12+0.09 | 75.96-4.06+6.20 | -2.12-0.05+0.03 | - | 465.8/348 | 489.22 | 6.93-0.71+0.63 | |
| SBPL | -3.30-0.04+0.04 | 1.42-0.00+0.01 | 5012.91-121.72+539.43 | 8.67-0.31+0.34 | -0.12-0.00+0.00 | 802.82/358 | 832.30 | 0.77-0.01+0.03 | ||
| BPL | -0.48-0.01+0.05 | 1.07-0.01+0.01 | 59.74-5.73+2.77 | 2.15-0.03+0.06 | - | 503.14/359 | 526.71 | 0.87-0.11+0.03 | ||
| 3.13:3.91 | Band | -0.07-0.04+0.04 | -0.48-0.05+0.05 | 135.77-6.48+7.56 | -2.05-0.03+0.02 | - | 359.6/348 | 383.09 | 1.90-0.01+0.03 | |
| SBPL | 0.06-0.07+0.04 | 0.36-0.86+0.05 | 61.21-5.39+5.39 | 2.18-1.61+0.01 | 0.92-0.03+0.19 | 391.90/358 | 421.37 | 2.30-0.13+0.18 | ||
| BPL | -0.40-0.07+0.02 | 0.89-0.00+0.01 | 84.74-4.42+2.80 | 2.02-0.02+0.01 | - | 450.56/359 | 474.14 | 2.50-0.13+0.15 | ||
| 3.91:4.70 | Band | 0.08-0.01+0.01 | -0.46-0.02+0.02 | 374.28-8.35+7.34 | -2.52-0.04+0.03 | - | 562.4/348 | 585.81 | 7.35-0.20+0.22 | |
| SBPL | -0.11-0.02+0.01 | 2.78-2.45+0.01 | 270.78-19.33+7.05 | 0.43-0.01+1.18 | 0.59-0.01+0.02 | 551.19/358 | 580.66 | 9.28-0.24+0.30 | ||
| BPL | -0.32-0.02+0.03 | 0.71-0.01+0.01 | 200.75-2.12+8.27 | 2.23-0.01+0.01 | - | 1085.7/359 | 1109.28 | 10.2-0.29+0.29 | ||
| 4.70:5.48 | Band | 0.32-0.00+0.00 | -0.33-0.01+0.01 | 551.37-6.90+6.44 | -2.73-0.03+0.03 | - | 1186.4/348 | 1209.83 | 22.3-0.1+0.3 | |
| SBPL | 0.32-0.01+0.01 | 0.15-0.02+0.02 | 525.15-46.41+18.96 | 3.56-0.12+0.05 | 0.31-0.01+0.02 | 843.62/358 | 873.10 | 28.6-0.03+0.03 | ||
| BPL | -0.12-0.01+0.04 | 0.58-0.02+0.01 | 296.39-2.31+2.56 | 2.31-0.01+0.01 | - | 2864.7/359 | 2888.29 | 30.4-0.04+0.05 | ||
| 5.48:6.26 | Band | 0.39-0.01+0.01 | -0.42-0.01+0.01 | 424.45-8.27+6.35 | -2.42-0.02+0.02 | - | 1225.2/348 | 1248.65 | 19.3-0.3+0.3 | |
| SBPL | 0.36-0.01+0.01 | 0.27-0.01+0.01 | 302.97-1.59+14.59 | 2.92-0.05+0.05 | 0.44-0.01+0.01 | 835.11/358 | 864.58 | 24.3-0.04+0.03 | ||
| BPL | -0.001-0.00+0.00 | 0.66-0.01+0.02 | 213.47-0.36+1.61 | 2.16-0.01+0.01 | - | 2419.4/359 | 2443.0 | 26.4-0.01+0.03 | ||
| 6.26:7.04 | Band | 0.34-0.01+0.00 | -0.41-0.01+0.01 | 574.69-6.82+11.94 | -2.50-0.03+0.02 | - | 1768.1/348 | 1791.59 | 26.3-0.4+0.4 | |
| SBPL | 0.20-0.01+0.01 | 0.28-0.01+0.01 | 700.42-18.35+78.35 | 3.64-0.04+0.16 | 0.29-0.02+0.01 | 1183.9/358 | 1213.44 | 33.5-0.06+0.03 | ||
| BPL | -0.04-0.02+0.01 | 0.60-0.01+0.02 | 262.79-8.92+1.45 | 2.13-0.01+0.02 | - | 3625.6/359 | 3649.25 | 36.1-0.01+0.03 | ||
| 7.04:7.83 | Band | 0.27-0.00+0.00 | -0.42-0.01+0.01 | 722.10-12.02+8.62 | -2.71-0.03+0.03 | - | 1869.7/348 | 1893.18 | 28.7-0.01+0.03 | |
| SBPL | 0.20-0.01+0.00 | 0.23-0.01+0.01 | 654.88-15.51+15.51 | 3.42-0.06+0.01 | 0.32-4.89+0.01 | 1249.8/358 | 1279.29 | 37.6-0.06+0.05 | ||
| BPL | -0.18-0.02+0.01 | 0.61-0.01+0.02 | 347.31-10.87+3.92 | 2.23-0.01+0.01 | - | 3926.9/359 | 3950.55 | 38.8-0.01+0.03 | ||
| 7.83:8.61 | Band | 0.28-0.00+0.00 | -0.44-0.01+0.01 | 718.53-9.32+9.42 | -2.87-0.05+0.03 | - | 1662.9/348 | 1686.36 | 27.1-0.04+0.03 | |
| SBPL | -0.002-0.00+0.00 | 3.46-0.05+0.02 | 682.43-6.07+1.69 | 0.37-0.01+0.01 | 0.39-0.01+0.01 | 1318.6/358 | 1348.16 | 35.2-0.4+0.5 | ||
| BPL | -0.21-0.01+0.02 | 0.64-0.00+0.02 | 366.34-13.12+2.85 | 2.32-0.01+0.03 | - | 3835.7/359 | 3859.33 | 36.8-0.01+0.03 | ||
| 8.61:9.39 | Band | -0.30-0.00+0.00 | -0.47-0.01+0.01 | 683.29-9.76+9.65 | -2.78-0.03+0.04 | - | 1761.5/348 | 1784.92 | 26.6-0.01+0.03 | |
| SBPL | 0.20-0.02+0.02 | 3.20-0.04+0.01 | 524.69-21.58+16.71 | 0.28-0.01+0.01 | 0.38-0.01+0.01 | 1222.7/358 | 1252.23 | 34.8-0.01+0.03 | ||
| BPL | -0.17-0.01+0.01 | 0.66-0.01+0.02 | 332.26-3.52+9.18 | 2.25-0.02+0.05 | - | 3924.2/359 | 3947.74 | 36.3-0.01+0.03 | ||
| 9.39:10.2 | Band | 0.26-0.00+0.00 | -0.46-0.01+0.01 | 759.74-8.14+12.00 | -2.82-0.04+0.04 | - | 1567.4/348 | 1590.8 | 28.5-0.01+0.03 | |
| SBPL | 0.10-0.01+0.01 | 3.31-0.01+0.01 | 621.54-3.04+2.44 | 0.30-0.01+0.01 | 0.38-0.01+0.01 | 1228.4/358 | 1257.84 | 36.9-0.01+0.03 | ||
| BPL | -0.25-0.01+0.01 | 0.66-0.02+0.01 | 387.71-5.26+3.10 | 2.31-0.01+0.02 | - | 3706.7/359 | 3730.34 | 38.4-0.06+0.03 | ||
| 10.17:10.96 | Band | 0.35-0.01+0.00 | -0.51-0.01+0.01 | 545.41-7.83+10.98 | -2.49-0.04+0.02 | - | 1562.9/348 | 1586.36 | 23.8-0.4+0.4 | |
| SBPL | 0.28-0.01+0.41 | 2.97-0.03+0.01 | 398.99-13.21+0.41 | 0.33-0.01+0.01 | -0.41-0.01+0.01 | 1019.6/358 | 1049.04 | 30.9-0.45+0.42 | ||
| BPL | -0.03-0.01+0.01 | 0.67-0.00+0.01 | 239.79-3.20+2.42 | 2.11-0.01+0.01 | - | 3185.9/359 | 3209.51 | 32.9-0.05+0.03 | ||
| 10.96:11.74 | Band | 0.39-0.01+0.01 | -0.52-0.02+0.02 | 275.17-5.73+5.64 | -2.22-0.02+0.01 | - | 792.4/348 | 815.88 | 12.0-0.3+0.3 | |
| SBPL | 0.28-0.05+0.01 | 2.42-0.04+0.02 | 158.82-7.64+5.78 | 0.50-0.01+0.01 | 0.78-0.01+0.05 | 725.02/358 | 754.49 | 15.0-0.1+0.2 | ||
| BPL | -0.001-0.05+5.31 | 0.82-0.01+0.02 | 155.08-0.36+1.23 | 2.11-0.01+0.03 | - | 1494.2/359 | 1517.76 | 16.1-0.01+0.3 | ||
| 11.74:12.52 | Band | 0.25-0.03+0.04 | -0.56-0.04+0.05 | 103.64-4.16+3.43 | -2.19-0.03+0.02 | - | 384.7/348 | 408.19 | 2.46-0.1+0.03 | |
| SBPL | 0.37-0.13+0.35 | 0.49-0.07+0.16 | 52.97-2.16+6.17 | 2.30-0.01+0.04 | 1.05-0.13+0.35 | 455.31/358 | 484.78 | 3.01-0.01+0.03 | ||
| BPL | -0.01-0.02+0.01 | 0.98-0.03+0.01 | 68.20-0.69+2.02 | 2.14-0.03+0.03 | - | 549.21/359 | 572.79 | 3.28-0.01+0.13 | ||
| 12.52:13.30 | Band | 0.08-0.02+0.02 | -0.72-0.02+0.02 | 236.20-8.00+8.13 | -2.14-0.02+0.03 | - | 527.7/348 | 551.13 | 5.49-0.01+0.03 | |
| SBPL | 0.01-0.01+0.01 | 2.33-0.02+0.01 | 129.16-4.57+4.57 | 0.68-0.02+0.01 | 0.91-0.01+0.04 | 531.51/358 | 560.98 | 6.76-0.01+0.33 | ||
| BPL | -0.17-0.01+0.01 | 0.93-0.01+0.01 | 115.78-3.76+2.36 | 2.02-0.01+0.02 | - | 778.56/359 | 802.14 | 7.56-0.20+0.22 | ||
| 13.30:14.09 | Band | 0.21-0.06+0.07 | -0.55-0.07+0.07 | 74.45-3.34+3.20 | -2.16-0.02+0.02 | - | 415.8/348 | 439.27 | 1.48-0.1+0.1 | |
| SBPL | -1.17-0.02+0.02 | 1.36-0.01+0.01 | 310.43-13.89+13.89 | 3.66-0.01+0.15 | 0.66-0.05+0.01 | 859.39/358 | 888.86 | 1.52-0.01+0.08 | ||
| BPL | -0.05-0.03+0.02 | 1.07-0.00+0.01 | 53.17-2.33+1.34 | 2.13-0.02+0.02 | - | 489.71/359 | 513.29 | 1.96-0.09+0.03 | ||
| 14.09:14.87 | Band | -0.44-0.02+0.00 | -1.16-0.02+0.01 | 58.22-1.75+1.75 | -2.05-0.03+0.01 | - | 513.0/348 | 536.50 | 0.80-0.01+0.07 | |
| SBPL | -3.99-0.04+0.25 | 3.21-0.29+0.33 | 6751.19-1166.05+1069.56 | 1.70-0.01+0.01 | 0.34-0.01+0.13 | 729.06/358 | 758.53 | 1.13-0.01+0.12 | ||
| BPL | -3.83-0.39+0.03 | 1.84-0.01+0.01 | 3309.92-3.24+2107.91 | 2.07-6.61+0.72 | - | 767.69/359 | 791.27 | 1.45-0.01+0.11 |
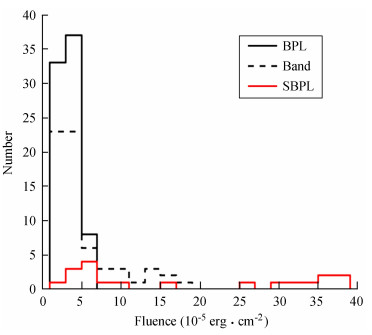
由图 1和表 3可以看出,折线幂率模型、波段函数模型和平滑拐折幂率模型拟合的伽玛暴的能流分布中间值分别为2.24×10-5erg·cm-2、2.61×10-5erg·cm-2和9.28×10-5erg·cm-2。然而当Fe < 5×10-5erg·cm-2时,折线幂率模型拟合得最好,当5×10-5erg·cm-2 < Fe < 2.0×10-4erg·cm-2时,波段函数模型拟合得最好,当2.0×10-4erg·cm-2 < Fe < 3.8×10-4erg·cm-2时,平滑拐折幂率模型拟合得最好。平滑拐折幂率模型可以很好地拟合能流范围广且数值比较大的数据,主要因为该模型引入了一个描述能谱拐折的量w,表示该模型在能谱峰附近曲率比较灵活,它对谱拐折比较尖锐或光滑的能谱都能较好地拟合,但在能流较小的数据中,折线幂率模型优于平滑拐折幂率模型(文后有详细描述)。因此,能流较小的数据可以用折线幂率模型很好地拟合,能流较大的数据可以用平滑拐折幂率模型和波段函数模型很好地拟合。此外,表 4显示了165个最佳拟合谱中各模型拟合能谱的数目,可以看到样本中接近一半的能谱可以用折线幂率模型很好地拟合,表明有些暴的谱形状接近折线,尤其是较暗的暴,即这些伽玛暴能谱的谱拐折比较尖锐。
|
| 图 1 所有时间分辨谱能量(1~104keV)的分布,最佳拟合模型用不同的颜色表示 Fig. 1 The distribution of fluence (1~104keV) for all time-resolved spectra, the best-fit model is represented by different colors |
| Best-model | Fluence(10-5 erg•cm-2) | ||
| Band | SBPL | BPL | |
| Median | 2.61 | 9.28 | 2.24 |
| Best-model | Band | BPL | SBPL | All spectra |
| Sample size | 65 | 78 | 22 | 165 |
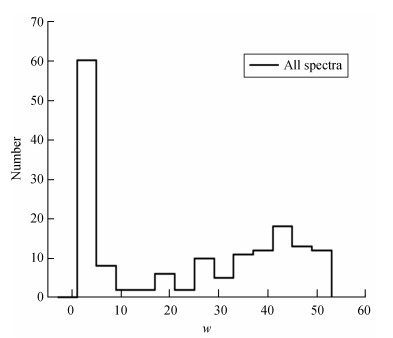
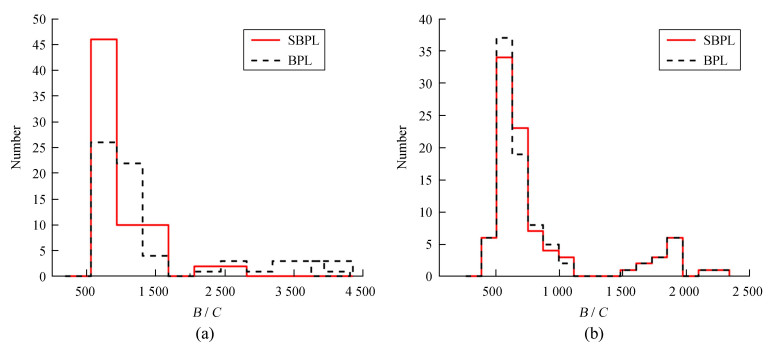
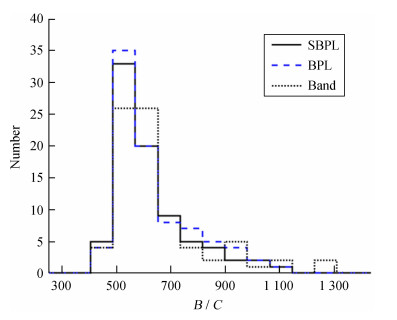
图 2给出平滑拐折幂率模型拟合所有时间分辨谱得到的w参数分布,可以看出w呈双峰分布(0~10和10~50)。图 3显示两个峰内平滑拐折幂率模型和折线幂率模型拟合数据得到的BIC值的分布。w分布在第1个峰时,平滑拐折幂率模型拟合优于折线幂率模型(图 3(a)),在第2个峰时平滑拐折幂率模型和折线幂率模型拟合结果基本一致(图 3(b)),但在这部分谱中最佳拟合模型是折线幂率模型。这表明参数w的值越大,光谱拐折越尖锐,如GRB 100826,折线幂率模型拟合得更好;w越小光谱拐折越平滑,如GRB 130427,平滑拐折幂率模型拟合得更好。此外,当Fe < 4×10-5erg·cm-2时,能谱的最佳拟合模型是折线幂率模型,但波段函数模型和平滑拐折幂率模型也有相似的拟合优度(图 4是3个模型在这个能流区域内拟合数据的贝叶斯信息准则分布),表明现有的数据不能很好地剔除一些光子模型。另外,从图 5可以看出,高能端光子数特别少,高能幂率指数得不到很好的限制,在表 2中β的误差也比较大,因此,拟合结果受高能部分有限光子数的影响,所以在进行光谱分析时需要更高质量和更多数量的高能光子,也就是需要有更高的时间分辨率和能量分辨率的仪器探测到更多的光子。
|
| 图 2 平滑拐折幂率模型参数w的分布 Fig. 2 Distribution of parameter w of SBPL model |
|
| 图 3 (a) 参数w在0~10之间平滑拐折幂率模型和折线幂率模型的贝叶斯信息准则分布;(b)参数w在10~50之间平滑拐折幂率模型和折线幂率模型的贝叶斯信息准则分布 Fig. 3 (a) BIC distribution of SBPL and BPL models with parameter w between 0~10; (b) BIC distribution of SBPL and BPL models with parameter w between 10~50 |
|
| 图 4 能流在0~4×10-5erg·cm-2之间3个模型拟合数据的贝叶斯信息准则分布 Fig. 4 Fluence is between 0~4×10-5erg·cm-2, the BIC distribution of the three models fits the data |
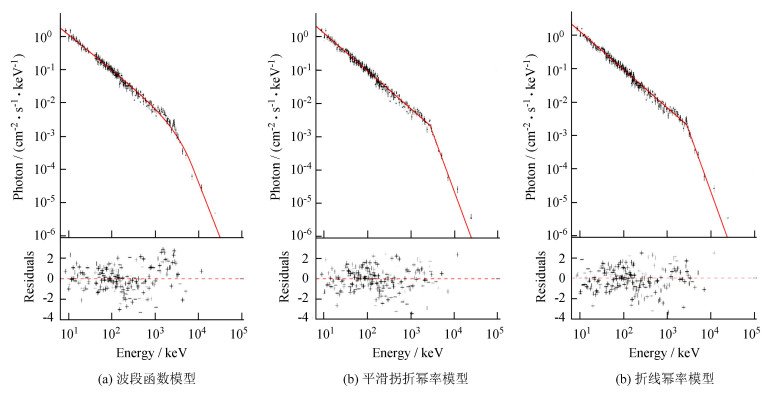
|
| 图 5 3个模型分别拟合GRB 100826(21.25: 22.00s)一段时间的光子谱 Fig. 5 Three models are shown to fit GRB 100826 (21.25: 22.00s) photon spectrum for a period of time |
本文使用平滑拐折幂率模型、折线幂率模型和波段函数模型拟合8个费米亮暴的时间分辨光谱数据,得到165个最佳模型拟合谱。通过比较几个模型的拟合结果得到折线幂率模型能很好地拟合较暗的暴,平滑拐折幂率模型和波段函数模型可以拟合较亮的暴。在样本中有一半谱可以用折线幂率模型拟合,即当用经验模型拟合谱时发现折线幂率模型比波段函数模型拟合得好,这意味着有些暴(特别是相对较暗的暴)的谱形接近折线形状,表明观测光谱的谱拐折比较尖锐,以至于同步模型难以解释伽玛暴能谱[11-12]。另外,平滑拐折幂率模型参数w的值越大(10~50),谱拐折越尖锐,此时平滑拐折幂率模型和折线幂率模型的拟合结果基本一致(如GRB 100826),但折线幂率模型是最佳拟合模型。w越小(0~10),谱拐折越平滑(如GRB 130427),平滑拐折幂率模型和波段函数模型的拟合优于折线幂率模型。当Fe < 4×10-5erg·cm-2时能谱最佳拟合模型是折线幂率模型,波段函数模型和平滑拐折幂率模型拟合这部分数据虽然不是最优,但也得到可以接受的拟合结果,说明现有的数据不能很好地剔除这些光子模型。
此外,模型对GRB 130427的部分拟合不是很好,贝叶斯信息准则值比较大,这种情况表明,可能存在较强的谱演化。能谱拟合受有限光子数和拟合模型自身的影响,光子数少使高能谱指数得不到准确限制,影响高能光谱形状。模型作为数据的代理会导致偏差,模型间接影响光谱的形状,并且这些模型都是数学函数,它们不能真实反映伽玛暴的物理机制。另一方面,拟合受仪器响应矩阵的限制,不能很好地确定伽玛暴真实的物理模型。如果将来消除了仪器响应矩阵的影响并且仪器的时间分辨率和能量分辨率有所提高,可以观测到更多更高精度的数据,将极大促进伽玛暴物理机制的研究。
| [1] | 黄舜. Fermi伽玛射线暴瞬时辐射热成分研究[D].云南: 云南师范大学, 2017. HUANG S. Investigating the thermal component in the prompt eission of Fermi Gamma-Ray Bursts[D]. Yunnan: Yunnan Normal University, 2017. |
| [2] | GUIRIEC S, CONNAUGHTON V, BRIGGS M S, et al. Detection of a thermal spectral component in the prompt emission of GRB 100724B[J]. The Astrophysical Journal, 2011, 727(2): 581–586. |
| [3] | PIRAN T, SARI R, ZOU Y C. Observational limits on inverse Compton processes in gamma-ray bursts[J]. Monthly Notices of the Royal Astronomical Society, 2009, 393(4): 1107–1113. DOI: 10.1111/j.1365-2966.2008.14198.x |
| [4] | REES M J, MÉSZÁROS P. Unsteady outflow models for cosmological gamma-raybursts[J]. The Astrophysical Journal, 1994, 430(2): L93–L96. |
| [5] | ZHANG B, MÉSZÁROS P. Gamma-Ray Bursts:progress, problems & prospects[J]. International Journal of Modern Physics A, 2004, 19(15): 2385–2472. DOI: 10.1142/S0217751X0401746X |
| [6] | ZHANG B, YAN H R. The Internal-Collision-Induced Magnetic Reconnection and Turbulence (ICMART) model of Gamma-Ray Bursts[J]. The Astrophysical Journal, 2010, 726(2): 380–391. |
| [7] | ZHANG B, ZHANG B. Gamma-Ray Burst prompt emission light curves and power density spectra in the ICMART model[J]. The Astrophysical Journal, 2014, 782(2): 92. DOI: 10.1088/0004-637X/782/2/92 |
| [8] | BAND D, MATTERSON J, FORD L, et al. BATSE observations of gamma-ray burst spectral diversity[J]. The Astrophysical Journal, 1993, 413(1): 281–292. |
| [9] | YU H F, PREECE R D, GREINER J, et al. The Fermi GBM gamma-ray burst time-resolved spectral catalog:brightest bursts in the first four years[J]. Astronomy & Astrophysics, 2016, 588: 135–190. |
| [10] | KANEKO Y, PREECE R D, BRIGGS M S, et al. The complete spectral catalog of bright BATSE gamma-ray bursts[J]. The Astrophysical Journal Supplement Series, 2006, 166(1): 298–340. DOI: 10.1086/505911 |
| [11] | AXELSSON M, BORGONOVO L. The width of gamma-ray burst spectra[J]. Monthly Notices of the Royal Astronomical Society, 2015, 447(1): 3150–3154. |
| [12] | YU H F, VAN EERTEN H J, GREINER J, et al. The sharpness of gamma-ray burst prompt emission spectra[J]. Astronomy and Astrophysics, 2015, 583: 129–145. DOI: 10.1051/0004-6361/201527015 |
| [13] | MEEGAN C, LICHTI G, BHAT P N, et al. The Fermi Gamma-Ray Burst Monitor[J]. The Astrophysical Journal, 2009, 702(1): 791–804. DOI: 10.1088/0004-637X/702/1/791 |
| [14] | ZHANG B B, UHM Z L, CONNAUGHTON V, et al. Synchrotron origin of the typical GRB band function-a case study of GRB 130606B[J]. The Astrophysical Journal, 2016, 816: 72–83. DOI: 10.3847/0004-637X/816/2/72 |
| [15] | RAVASIO M E, OGANESYAN G, GHIRLANDA G, et al. Consistency with synchrotron emission in the bright GRB 160625B observed by Fermi[J]. Astronomy & Astrophysics, 2017, 613: A16. |



