2. 中国科学院大学, 北京 100049;
3. 中国科学院 FAST重点实验室, 北京 100101;
4. 中国科学院月球与深空探测重点实验室, 北京 100101
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of FAST, Chinese Academy of Sciences, Beijing 100101, China;
4. Key Laboratory of Lunar and Deep Space Exploration, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China
指向精度是反射面天线最重要的性能指标之一,为保证天线的接收效率,要求指向误差小于波束宽度的1/10,指向精度与天线口径及频率成反比,大口径高频率天线对指向精度的最高要求达到角秒级[1-2]。目前世界上最大的全可动天线是美国100 m绿岸射电望远镜,频率范围从300 MHz到115 GHz,高频(100 GHz以上)观测时,要求跟踪误差小于1.5″[3]。我国在建的天津武清70 m天线Ku频段的指向精度要求为13″,后续扩展为Ka频段的指向精度要求为3.5″。计划建设的新疆奇台超大型全可动天线,口径达到110 m,频率达到115 GHz,预期最高指向精度优于2.5″[4]。天线结构变形是影响指向精度的主要因素,天线最佳吻合面与副反射面横向偏移或转动、馈源横向偏移等均影响天线的指向精度[5-7]。天线初始指向不能满足精度要求,需准确评估天线的指向误差并通过软件进行校准[8],准确评估天线的指向误差非常重要。
使用基于高频方法和数值方法的电磁仿真算法能准确快速地评估电小尺寸天线的电性能,但分析电大尺寸天线时耗时较长,仅局限于天线的设计阶段。文[9]提出基于波束偏移因子(Beam Deviation Factor, BDF)评估天线指向误差的算法,该算法具有评估实时性,在国内外广泛使用。文[10]提出基于奇异值分解法确定馈源偏移量的算法,用于补偿反射面变形对电性能的影响。两种算法具有相似性,都是针对前馈式天线进行讨论。针对双反射面天线的指向误差评估,目前普遍采用的算法是将天线的耦合变形分解为天线主面变形、副面横向偏移或转动以及馈源横向偏移等单一变形,然后将各变形工况下的指向误差叠加,未考虑变形耦合特性对指向评估精度的影响[11]。文[12]应用虚焦点等效变换方法,将天线副面及馈源的横向偏移或转动等效为主焦点的横向偏移,考虑了天线的变形耦合特性,但未给出具体分析和验证。文[13]针对天线的副面校准,提出对复杂几何/物理光学分析的简化算法。文[14]提出应用焦散线分析波束偏移因子的算法。受此启发,本文针对大型天线变形具有耦合性的特点,提出基于几何光学(Geometric Optics, GO)的指向误差评估算法。首先建立天线的最佳吻合面、偏移副面以及馈源的数学模型并求解反射面辐射区间,然后确定指向误差权重因子和指向误差评估模型,最后进行算例分析和验证。
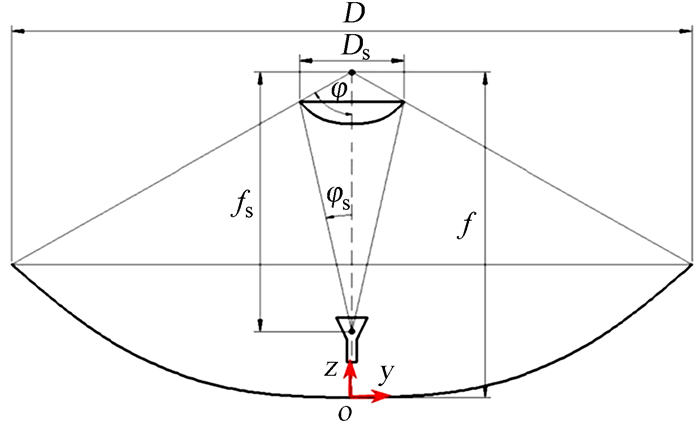
1 反射面天线数学模型及反射面辐射区间卡塞格林天线的几何图形如图 1,天线主面口径、主焦长、副面口径、馈源辐射半角等4个参数分别用符号D,f,Ds,φs表示。以抛物面顶点为原点建立基坐标系,抛物面开口方向为z轴正向,y轴向右。
|
| 图 1 卡塞格林天线几何平面图 Fig. 1 The geometry of Cassegrain antenna |
天线变形前,抛物面方程Fp为
| $ {F_{\rm{p}}}(x,y,z) = ({x^2} + {y^2})/(4f) - z = 0,\quad x,y \in [ - D/2,D/2], $ | (1) |
双曲面方程Fs为
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{\rm{s}}}(x,y,z) = [{{(z - f + c)}^2}]/{a^2} - ({x^2} + {y^2})/{b^2} - 1 = 0,}\\ {x,y \in [ - {D_2}/2,\quad {D_2}/2],z > f - c,} \end{array}} \right. $ | (2) |
其中,
天线发生微小变形后,忽略三角函数误差,最佳吻合抛物面方程Fp为
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{\rm{p}}}(x,y,z) = \frac{{{{[(x - \Delta x) - {\varphi _y}(z - \Delta z)]}^2} + [(y - \Delta y) + {\varphi _x}(z - \Delta z)]^2}}{{4(f + \Delta f)}} - }\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{\varphi _y}(x - \Delta x) - {\varphi _x}(y - \Delta y) + (z - \Delta z)] = 0}\\ {x \in [ - D/2 + {D^2}/(16f){\varphi _y} + \Delta x,D/2 + {D^2}/(16f){\varphi _y} + \Delta x]}\\ {y \in [ - D/2 - {D^2}/(16f){\varphi _x} + \Delta y,D/2 - {D^2}/(16f){\varphi _x} + \Delta y]} \end{array}} \right., $ | (3) |
其中,Δx,Δy,Δz分别为最佳吻合抛物面顶点相对设计抛物面顶点在x,y,z轴方向的位移偏差;φx,φy分别为两抛物面绕x,y轴的角位移偏差;Δf为焦距偏差。偏移双曲面方程Fs为:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{\rm{s}}}(x,y,z) = {{[{\varphi _{y1}}(x - \Delta {x_1}) - {\varphi _{x1}}(y - \Delta {y_1}) + (z - f) + c]}^2}/{a^2} - 1 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \{ {{[(x - \Delta {x_1}) - {\varphi _{y1}}(z - f)]}^2} + {{[(y - \Delta {y_1}) + {\varphi _{x1}}(z - f)]}^2}\} /{b^2} = 0}\\ {x \in [ - D/2 + {z_0}{\varphi _{y1}} + \Delta {x_1},D/2 + {z_0}{\varphi _{y1}} + \Delta {x_1}]}\\ \begin{array}{l} y \in [ - D/2 - {z_0}{\varphi _{x1}} + \Delta {y_1},D/2 - {z_0}{\varphi _{x1}} + \Delta {y_1}]\\ {z_0} = (a/2b\sqrt {4{b^2} + {D_{\rm{s}}}^2} - c + f),z > f - c \end{array} \end{array}} \right., $ | (4) |
其中,Δx1,Δy1分别为变形双曲面焦点相对设计双曲面焦点在x,y轴方向的位移;φx1,φy1分别为绕x,y轴的角位移。馈源偏移坐标(xk, yk, zk)变为(xk + Δxk, yk + Δyk, f-fs),其中,Δxk,Δyk为馈源分别在x,y轴方向的横向偏移量。
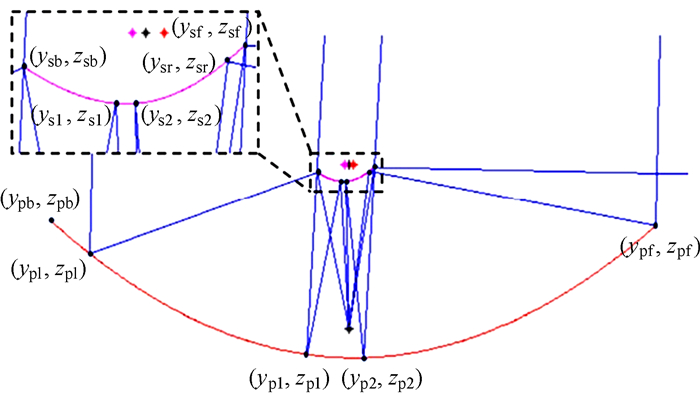
1.2 反射面辐射区间天线在口径面上的指向误差可分解为沿俯仰方向的指向误差和垂直于俯仰方向的指向误差。为便于描述,将天线投影到俯仰平面(yoz面)上,以下均只考虑天线在俯仰方向的指向误差,垂直俯仰方向的指向误差分析算法与之相似。如图 2,天线结构变形后,主反射面的边缘区域[ypb, ypl]接收不到由副面反射的散射光线,同时,由副面的边缘区域[ysr, ysf]反射的散射光线也不能被主反射面反射到空间。
|
| 图 2 反射面辐射区间 Fig. 2 The radiation interval of reflector |
对主面辐射区间,根据反射定理和副面左端点(ysb, zsb)建立方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {{{[({y_{{\rm{pl}}}} - \Delta y) + {\varphi _x}({z_{{\rm{pl}}}} - \Delta z)]}^2}/[4(f + \Delta f)] - {\varphi _x}({y_{{\rm{pl}}}} - \Delta y) - ({z_{{\rm{pl}}}} - \Delta z) = 0}\\ {{k_2}({y_{{\rm{pl}}}} - {y_{{\rm{sb}}}}) - ({z_{{\rm{pl}}}} - {z_{{\rm{sb}}}}) = 0}\\ {{k_{{\rm{nsb}}}} = \frac{{{\varphi _x}{a^2}[({y_{{\rm{sb}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{sb}}}} - f)] - {b^2}[({z_{{\rm{sb}}}} - f) + c - {\varphi _x}({y_{{\rm{sb}}}} - \Delta {y_1})]}}{{{\varphi _x}{b^2}[({z_{{\rm{sb}}}} - f) + c - {\varphi _x}({y_{{\rm{sb}}}} - \Delta {y_1})] + {a^2}[({y_{{\rm{sb}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{sb}}}} - f)]}}}\\ {{k_1} = ({z_{{\rm{sb}}}} - f + {f_{\rm{s}}})/({y_{{\rm{sb}}}} - {y_{\rm{k}}} - \Delta {y_{\rm{k}}})}\\ {{k_2} = ({k_1} - 2{k_{{\rm{nsb}}}} - {k_1}{k_{{\rm{nsb}}}}^2)/({k_{{\rm{nsb}}}}^2 - 2{k_{{\rm{nsb}}}}{k_1} - 1)} \end{array}} \right., $ | (5) |
其中,ypl,zpl,knsb,k1,k2未知,其余参数均已知。knsb为副面在左端点(ysb, zsb)的法线斜率;k1为馈源(yk + Δyk, f-fs)到副面边界点(ysb, zsb)的散射光线斜率;k2为副面边界点(ysb, zsb)到主面辐射点(ypl, zpl)的散射光线斜率。用牛顿法求解(5)式可确定ypl值,当ypl > ypb时,主面辐射左边界为ypl,反之则为ypb;同理可根据副面右端点(ysf, zsf)确定主面辐射右边界。
对副面辐射区间,根据反射定理和主面右端点(ypf, zpf)建立非线性方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {{{[({z_{{\rm{sr}}}} - f) + c - {\varphi _x}({y_{{\rm{sr}}}} - \Delta {y_1})]}^2}/{a^2} - {{[({y_{{\rm{sr}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{sr}}}} - f)]}^2}/{b^2} - 1 = 0}\\ {{k_2}({y_{{\rm{sr}}}} - {y_{{\rm{pf}}}}) - ({z_{{\rm{sr}}}} - {z_{{\rm{pf}}}}) = 0}\\ {{k_{{\rm{ns}}}} = \frac{{{\varphi _x}{a^2}[({y_{{\rm{sr}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{sr}}}} - f)] - {b^2}[({z_{{\rm{sr}}}} - f) + c - {\varphi _x}({y_{{\rm{sr}}}} - \Delta {y_1})]}}{{{\varphi _x}{b^2}[({z_{{\rm{sr}}}} - f) + c - {\varphi _x}({y_{{\rm{sr}}}} - \Delta {y_1})] + {a^2}[({y_{{\rm{sr}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{sr}}}} - f)]}}}\\ {{k_1} = ({z_{{\rm{sr}}}} - f + {f_{\rm{s}}})/({y_{{\rm{sr}}}} - {y_{\rm{k}}} - \Delta {y_{\rm{k}}})}\\ {{k_2} = ({k_1} - 2{k_{{\rm{ns}}}} - {k_1}{k_{{\rm{ns}}}}^2)/({k_{{\rm{ns}}}}^2 - 2{k_{{\rm{ns}}}}{k_1} - 1)} \end{array},} \right. $ | (6) |
其中,ysr,zsr,kns,k1,k2未知,其余参数均已知。kns为副面在反射点(ysr, zsr)的法线斜率;k1为馈源(yk + Δyk, f-fs)到副面反射点(ysr, zsr)的散射光线斜率;k2为副面反射点(ysr, zsr)到主面右端点(ypr, zpr)的散射光线斜率。求解(6)式可确定ysr值,当ysr < ysf时,副面辐射右边界为ysr,反之则为ysf;同理也可根据主面左端点(ypb, zpb)确定副面辐射左边界。
此外,正焦型反射面天线由于副面的遮挡,反射面的反射区间不连续。如图 2,主反射面的遮挡区间为[yp1, yp2],副反射面的遮挡区间为[ys1, ys2]。根据反射定理和副面左端点(ysb, zsb)建立非线性方程组:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{{[({z_{{\rm{s1}}}} - f) + c - {\varphi _x}({y_{{\rm{s1}}}} - \Delta {y_1})]}^2}/{a^2} - {{[({y_{{\rm{s1}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{s1}}}} - f)]}^2}/{b^2} - 1 = 0}\\ {{{[({y_{{\rm{p1}}}} - \Delta y) + {\varphi _x}({z_{{\rm{p1}}}} - \Delta z)]}^2}/[4(f + \Delta f)] - {\varphi _x}({y_{{\rm{p1}}}} - \Delta y) - ({z_{{\rm{p1}}}} - \Delta z) = 0} \end{array}\\ \begin{array}{*{20}{l}} {{k_{{\rm{ns1}}}} = \frac{{{\varphi _x}{a^2}[({y_{{\rm{s1}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{s1}}}} - f)] - {b^2}[({z_{{\rm{s1}}}} - f) + c - {\varphi _x}({y_{{\rm{s1}}}} - \Delta {y_1})]}}{{{\varphi _x}{b^2}[({z_{{\rm{s1}}}} - f) + c - {\varphi _x}({y_{{\rm{s1}}}} - \Delta {y_1})] + {a^2}[({y_{{\rm{s1}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{s1}}}} - f)]}}}\\ {{k_{{\rm{np1}}}} = \frac{{({y_{{\rm{p1}}}} - \Delta y){\varphi _x} + ({z_{{\rm{p1}}}} - \Delta z)\varphi _x^2 - 2(f + \Delta f)}}{{({y_{{\rm{p1}}}} - \Delta y) + ({z_{{\rm{p1}}}} - \Delta z){\varphi _x} + 2(f + \Delta f){\varphi _x}}}} \end{array}\\ \begin{array}{*{20}{l}} {{k_1} = ({z_{{\rm{s1}}}} - f + {f_{\rm{s}}})/({y_{{\rm{s1}}}} - {y_{\rm{k}}} - \Delta {y_{\rm{k}}})}\\ {{k_2} = ({z_{{\rm{p1}}}} - {z_{{\rm{s1}}}})/({y_{{\rm{p1}}}} - {y_{{\rm{s1}}}})}\\ {1/{k_3} = ({y_{{\rm{sb}}}} - {y_{{\rm{p1}}}})/({z_{{\rm{sb}}}} - {z_{{\rm{p1}}}})}\\ {{k_2} = ({k_1} - 2{k_{{\rm{ns1}}}} - {k_1}{k_{{\rm{ns1}}}}^2)/(k_{{\rm{ns1}}}^2 - 2{k_{{\rm{ns1}}}}{k_1} - 1)}\\ {1/{k_3} = ({k_{{\rm{np1}}}}^2 - 2{k_{{\rm{np1}}}}{k_2} - 1)/{k_2} - 2{k_{{\rm{np1}}}} - {k_2}{k_{{\rm{np1}}}}^2} \end{array} \end{array} \right., $ | (7) |
其中,ys1,zs1,yp1,zp1,kns1,knp1,k1,k2,1/k3未知,其余参数均已知。kns1为副面在反射点(ys1, zs1)的法线斜率;knp1为主面在反射点(yp1, zp1)的法线斜率;k1为馈源(yk + Δyk, f-fs)到副面反射点(ys1, zs1)的散射光线斜率;k2为副面反射点(ys1, zs1)到主面反射点(yp1, zp1)的散射光线斜率;k3为刚好过主面反射点(yp1, zp1)与副面左端点(ysb, zsb)的散射光线斜率。
求解(7)式可确定yp1和ys1值,yp1即为主面辐射遮挡区间的左边界,ys1即为副面辐射遮挡区间的左边界;同理,也可根据副面右端点(ysf, zsf)确定主、副反射面辐射遮挡区间的右边界。
综上所述,卡塞格林天线辐射区间为
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {{y_{\rm{p}}} \in [{y_{{\rm{pl}}}},{y_{{\rm{p1}}}}) \cup ({y_{{\rm{p2}}}},{y_{{\rm{pf}}}}],}\\ {{y_{\rm{s}}} \in [{y_{{\rm{sb}}}},{y_{{\rm{s1}}}}) \cup ({y_{{\rm{s2}}}},{y_{{\rm{sr}}}}],} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_{{\rm{pl}}}} > {y_{{\rm{pb}}}}{\rm{ 且 }}{y_{{\rm{pr}}}} > {y_{{\rm{pf}}}}} \right.\\ \left\{ {\begin{array}{*{20}{l}} {{y_{\rm{p}}} \in [{y_{{\rm{pb}}}},{y_{{\rm{p1}}}}) \cup ({y_{{\rm{p2}}}},\quad {y_{{\rm{pr}}}}],}\\ {{y_{\rm{s}}} \in [{y_{{\rm{sl}}}},{y_{{\rm{s1}}}}) \cup ({y_{{\rm{s2}}}},{y_{{\rm{sf}}}}],} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {y_{{\rm{pl}}}} < {y_{{\rm{pb}}}}{\rm{ 且 }}{y_{{\rm{pr}}}} < {y_{{\rm{pf}}}}} \right. \end{array}. $ | (8) |
天线变形会导致反射面散焦,抛物面上不同散射光线互不平行。根据锥销电平Te,对符合高斯分布的波束照明函数F(r)进行调整,取函数曲线的部分离散点作为指向误差权重因子di作用到从主面到空间的散射光线对应的指向误差δyi上,多条散射光线对应指向误差的加权组合即为天线在yoz面的耦合指向误差δy。
2.1 指向误差权重因子符合高斯分布的波束照明函数F(r)为
| $ F(r) = {\rm{exp}}\{ - \alpha {r^2}\} , $ | (9) |
其中,α=(Te/20)ln10[15]。考虑波束半径r=1时照明函数值F(1)刚好等于锥销系数(τe=10Te/20),使得天线辐射边界与波束锥销电平Te对应,故需对天线主面辐射半区间(假定ypl > ypb且ypr > ypf)进行归一化处理。通过构建指向调整系数β对照明函数F(r)进行调整,所得新函数曲线上的离散点ri对应函数值即为天线主面辐射区间上第i条散射光线对应的指向误差权重因子di为
| $ {d_i} = \frac{{{\rm{exp}}\{ - \alpha {{[{r_i} - ({r_{{\rm{pf}}}} - {r_{{\rm{pl}}}})/2]}^2}\} + \beta }}{{1 + \beta }}, $ | (10) |
其中,α=(Te/20)ln(10);ri=yi/[ypf-(ypf-ypl)/2];β=-(10Te/20-0.001)/(1-0.001)。
2.2 指向误差评估模型由主面辐射区间上的坐标点(ypi, zpi),可唯一确定从馈源发射并经过主、副反射面反射到空间的一条散射光线i,根据反射定理建立方程组:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{{[({z_{{\rm{si}}}} - f) + c - {\varphi _x}({y_{{\rm{si}}}} - \Delta {y_1})]}^2}/{a^2} - {{[({y_{{\rm{si}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{si}}}} - f)]}^2}/{b^2} - 1 = 0}\\ {{k_{{\rm{nsi}}}} = \frac{{{\varphi _x}{a^2}[({y_{{\rm{si}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{si}}}} - f)] - {b^2}[({z_{{\rm{si}}}} - f) + c - {\varphi _x}({y_{{\rm{si}}}} - \Delta {y_1})]}}{{{\varphi _x}{b^2}[({z_{{\rm{si}}}} - f) + c - {\varphi _x}({y_{{\rm{si}}}} - \Delta {y_1})] + {a^2}[({y_{{\rm{si}}}} - \Delta {y_1}) + {\varphi _x}({z_{{\rm{si}}}} - f)]}}} \end{array}\\ \begin{array}{*{20}{l}} {{k_{{\rm{npi}}}} = \frac{{({y_{{\rm{pi}}}} - \Delta y){\varphi _x} + ({z_{{\rm{pi}}}} - \Delta z)\varphi _x^2 - 2(f + \Delta f)}}{{({y_{{\rm{pi}}}} - \Delta y) + ({z_{{\rm{pi}}}} - \Delta z){\varphi _x} + 2(f + \Delta f){\varphi _x}}}}\\ {{k_{{\rm{1i}}}} = ({z_{{\rm{si}}}} - f + {f_{\rm{s}}})/({y_{{\rm{si}}}} - {y_{\rm{k}}} - \Delta {y_{\rm{k}}})} \end{array}\\ \begin{array}{*{20}{l}} {{k_{{\rm{2i}}}} = ({z_{{\rm{pi}}}} - {z_{{\rm{si}}}})/({y_{{\rm{pi}}}} - {y_{{\rm{si}}}})}\\ {{k_{{\rm{2i}}}} = ({k_{{\rm{1i}}}} - 2{k_{{\rm{nsi}}}} - {k_{{\rm{1i}}}}{k_{{\rm{nsi}}}}^2)/({k_{{\rm{nsi}}}}^2 - 2{k_{{\rm{nsi}}}}{k_{{\rm{1i}}}} - 1)}\\ {1/{k_{{\rm{3i}}}} = ({k_{{\rm{npi}}}}^2 - 2{k_{{\rm{npi}}}}{k_{{\rm{2i}}}} - 1)/({k_{{\rm{2i}}}} - 2{k_{{\rm{npi}}}} - {k_{{\rm{2i}}}}{k_{{\rm{npi}}}}^2)} \end{array} \end{array} \right., $ | (11) |
其中,ysi,zsi,knsi,knpi,k1i,k2i,1/k3i未知,其余参数均已知。(ysi, zsi)为散射光线i在副面上的反射点;knsi为副面在(ysi, zsi)点的法线斜率;knpi为主面在(ypi, zpi)点的法线斜率;k1i为馈源(yk + Δyk, f-fs)到副面(ysi, zsi)点的散射光线斜率;k2i为副面(ysi, zsi)点到主面(ypi, zpi)点的散射光线斜率;k3i为主面(ypi, zpi)点到空间的散射光线斜率。由(11)式可得散射光线i在空间的斜率k3i,理想反射面天线辐射到空间的波束指向平行于z轴,斜率k趋于无穷,由三角公式推导散射光线i的指向误差δyi为
| $ {\delta _{{\rm{yi}}}} = \mathop {{\rm{lim}}}\limits_{k \to + \infty } ({k_{{\rm{3i}}}} - k)/(1 + k{k_3}) = - 1/{k_{{\rm{3i}}}}. $ | (12) |
在天线主面辐射区间上取n个均匀分布的点,将各点对应指向误差权重因子di作用到对应指向误差δyi上,可推导出天线在yoz面上的指向误差评估模型:
| $ {\delta _{\rm{y}}} = \sum\limits_{i = 1}^n {{d_i}} {\delta _{{\rm{yi}}}}/\sum\limits_{i = 1}^n {{d_i}} = \sum\limits_{i = 1}^n {( - {d_i}/{k_{{\rm{3i}}}})} /\sum\limits_{i = 1}^n {{d_i}} . $ | (13) |
天津武清正在建设一座大型卡塞格林天线,基本参数为主面口径D=70 m、主焦f=21 m、副面口径Ds=6.6 m、馈源辐射半角φs=10.8°,拟定标校频段的波长λ=0.075 m、锥销电平Te=-12 dB。为验证几何光学算法的正确性,根据上述模型用波束偏移因子算法和电磁仿真算法分别对70 m天线在yoz面任意虚拟变形工况下的指向误差进行评估,结果基本吻合。因篇幅受限,本例仅对其中6组虚拟变形工况进行阐述,各参数如表 1。在yoz面,仅主面横向偏移Δy、转动φx、副面横向偏移Δy1、转动φx1以及馈源横向偏移Δyk等5个参量对天线俯仰指向精度有较大影响。考虑馈源横向偏移量Δyk很小,实际运行中很少对其进行补偿,故6组变形工况对应参数中除Δy,φx,Δy1,φx1等4个参数取值不为0外,其余参数均为0。为便于研究天线不同程度变形对指向精度的影响,使6组变形工况对应4项变形参数Δy,φx,Δy1,φx1均呈等差增长。
| Deformation conditions | Δx | Δy | Δz | φx | φy | Δf | Δxk | Δyk | Δx1 | Δy1 | φx1 | φy1 |
| 1 | 0 | 0.1λ | 0 | 0.06° | 0 | 0 | 0 | 0 | 0 | -0.2λ | 0.6° | 0 |
| 2 | 0 | 0.15λ | 0 | 0.08° | 0 | 0 | 0 | 0 | 0 | -0.25λ | 0.8° | 0 |
| 3 | 0 | 0.2λ | 0 | 0.1° | 0 | 0 | 0 | 0 | 0 | -0.3λ | 1° | 0 |
| 4 | 0 | 0.25λ | 0 | 0.12° | 0 | 0 | 0 | 0 | 0 | -0.35λ | 1.2° | 0 |
| 5 | 0 | 0.3λ | 0 | 0.14° | 0 | 0 | 0 | 0 | 0 | -0.4λ | 1.4° | 0 |
| 6 | 0 | 0.35λ | 0 | 0.16° | 0 | 0 | 0 | 0 | 0 | -0.45λ | 1.6° | 0 |
根据表 1中的参数,可由(5)~(8)式求解反射面辐射区间。本例在70 m天线的主面辐射区间上取41个均匀分布点(大的主面辐射半区间多取一个点),由(9)~(13)式求出虚拟变形工况下的指向误差δy,如表 2。
| Deformation conditions | 1 | 2 | 3 | 4 | 5 | 6 |
| Pointing errors δy for GO algorithm | 21.202 722″ | 26.903 479″ | 32.619 410″ | 38.354 208″ | 44.111 384″ | 49.894 229″ |
| Pointing errors δyfor BDF algorithm | 21.151 719″ | 26.816 458″ | 32.481 196″ | 38.145 935″ | 43.810 674″ | 49.475 412″ |
| Pointing errors δy for electromagnetic simulation algorithm | 21.264 708″ | 27.024 900″ | 32.689 089″ | 38.449 281″ | 44.209 472″ | 49.969 666″ |
波束偏移因子与天线的焦径比f/D以及锥销电平Te有关,其表达式为[15]
| $ \begin{array}{*{20}{l}} {BDF = \frac{{48}}{{1 + 2\tau }}{{(f/D)}^2}[[1 - 32{{(f/D)}^2}( - 1 + \tau ) + \tau ] + 32{{(f/D)}^2} * }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [ - 1 + 16{{(f/D)}^2}( - 1 + \tau )]\{ - {\rm{ln}}{{(f/D)}^2} + {\rm{ln}}[1/16 + {{(f/D)}^2}]\} ],} \end{array} $ | (14) |
其中,τ=10Te/20。波束偏移因子算法未考虑天线的变形耦合特性对指向评估精度的影响,将天线耦合变形分解为最佳吻合抛物面的横向偏移Δy与旋转φx、副反射面的横向偏移Δy1以及绕焦点的旋转φx1、馈源的横向偏移Δyk等5种变形,各变形的分项指向误差为
| $ \begin{array}{*{20}{l}} {{\delta _{{\rm{py}}}} = - BD{F_{\rm{p}}}(\Delta y/f),\quad {\rm{ translation}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{primary}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta y}\\ {{\delta _{{\rm{p}}{\rm{\varphi}} }} = (1 + BD{F_{\rm{p}}}){\varphi _x},\quad {\rm{ rotation}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{primary}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _x}}\\ {{\delta _{{\rm{sy}}}} = (BD{F_{\rm{p}}} - BD{F_{\rm{s}}}/M)(\Delta {y_1}/f),\quad {\rm{ translation}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{secondary}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta {y_1}},\\ {{\delta _{{\rm{s}}{\rm{\varphi}} }} = - (BD{F_{\rm{s}}}/M)(2c/f){\varphi _{x1}},\quad {\rm{ rotation}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{secondary}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{x1}}}\\ {{\delta _{{\rm{ky}}}} = (BD{F_{\rm{s}}}/M)(\Delta {y_{\rm{k}}}/f),\quad {\rm{ translation}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{feed}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta {y_{\rm{k}}}} \end{array} $ | (15) |
所有分项指向误差叠加,即得到最终指向误差:
| $ {\delta _{\rm{y}}} = {\delta _{{\rm{py}}}} + {\delta _{{\rm{p}}{\rm{\varphi}} }} + {\delta _{{\rm{sy}}}} + {\delta _{{\rm{s}}{\rm{\varphi}} }} + {\delta _{{\rm{ky}}}}. $ | (16) |
根据表 1中的参数,应用波束偏移因子算法求得70 m天线虚拟变形工况下的指向误差δy,如表 2。
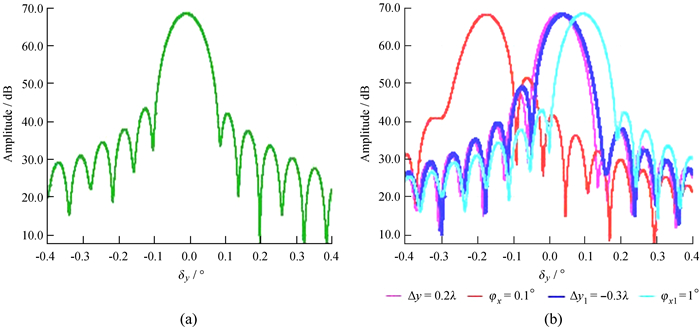
3.3 电磁仿真算法评估指向误差应用电磁仿真分析70 m天线虚拟变形工况下的指向误差δy如表 2。其中,第3组耦合变形下的指向误差δy=32.689 089″,方向图如图 3(a)。以该组变形工况为例,分析天线变形耦合特性对指向评估精度的影响。
|
| 图 3 70m天线的第3组虚拟变形工况对应方向图。(a)耦合变形方向图;(b)独立变形方向图 Fig. 3 The patterns for the third deformation conditions of 70-meter antenna. (a) The pattern for coupling deformation; (b) The patterns for single deformation |
首先将70 m天线的耦合变形分解为主面横向偏移Δy=0.2λ,主面绕顶点旋转φx=0.1°,副面横向偏移Δy1=-0.3λ,副面绕焦点旋转φx1=1°等4项独立变形。然后应用电磁仿真算法分别评估4项独立变形下的指向误差δpy,δpφ,δsy,δsφ,评估结果依次为-107. 379 579″,622.532 736″,-136.180 540″,-346.139 539″,方向图如图 3(b)。最后计算70 m天线因忽略耦合变形所导致的指向误差偏差:
| $ \Delta {\delta _y} = {\delta _{{\rm{py}}}} + {\delta _{{\rm{p}}{\rm{\varphi}} }} + {\delta _{{\rm{sy}}}} + {\delta _{{\rm{s}}{\rm{\varphi}} }} - {\delta _{\rm{y}}}, $ | (17) |
计算结果为0.143 988″。
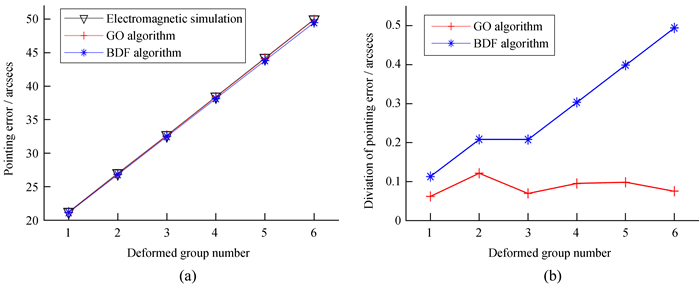
3.4 不同算法评估的指向误差及精度比较针对表 1中的参数,应用几何光学算法、波束偏移因子算法、电磁仿真算法评估70 m天线在6组虚拟变形工况下的指向误差,3类算法评估的指向误差对比图如图 4(a)。电磁仿真算法分析电大尺寸天线耗时长,但评估精度更高,故以电磁仿真算法的评估结果为基准,比较几何光学算法与波束偏移因子算法的指向评估精度,如图 4(b)。
|
| 图 4 不同算法评估的指向误差及精度比较。(a)3类算法评估的指向误差;(b)几何光学算法和波束偏移因子算法的评估精度 Fig. 4 The comparasion of pointing errors and estimation accuracy for different algorithms. (a) The pointing errors estimated by three algorithms; (b) The estimation accuracy for GO and BDF algorithm |
根据表 1提供的参数,天线变形量沿变形组号的递增序列依次呈等差增长。由图 4(a)可以得出,随着变形组号增加,指向误差呈相应增长趋势,且几何光学算法、波束偏移因子算法以及电磁仿真算法的指向误差评估结果一致。由图 4(b)可以得出,随着变形组号增加,天线变形量增大,波束偏移因子算法评估的指向误差偏差明显增大,其最大偏差值接近0.5″,而几何光学算法评估的指向误差偏差则相对稳定,始终保持在0.1″附近。
4 结束语通过对天线的最佳吻合抛物面、偏移副反射面以及馈源在基坐标下进行数学建模,计算反射面辐射区间并确定指向误差权重因子,最终建立双反射面天线的指向误差评估模型。应用该模型、波束偏移因子算法以及电磁仿真算法,对在建的武清70 m天线的多组虚拟变形工况进行指向误差评估。结果表明:3种算法评估的指向误差结果一致,且本文算法的评估精度较波束偏移因子算法的评估精度更优。由此得出以下结论:
(1) 本文提出基于几何光学建立大型双反射面天线指向误差评估模型的算法正确;
(2) 本文算法相对电磁仿真算法更高效,相对波束偏移因子算法更准确;
(3) 随着天线变形量增大,双反射面天线的变形耦合特性对指向评估精度的影响更显著,不容忽视。
本文为分析天线变形耦合特性对指向评估精度的影响提供了理论依据,也为实现天线动态指向误差实时评估提供了新思路。文中提出的大型双反射面天线指向误差评估算法,结合在建的武清70 m天线的多组虚拟变形工况进行了指向误差评估,评估结果可信。天线建成后,可针对实际测量的天线变形工况,应用本文算法对其进行指向误差评估,同时应用射电扫描法对该算法的评估精度作进一步验证。
| [1] | BOLLI P, ORFEI A, ZANICHELLI A, et al. An international survey of front-end receivers and observing performance of telescopes for radio astronomy[J]. Publications of the Astronomical Society of the Pacific, 2019, 131: 085002. DOI: 10.1088/1538-3873/ab1f7e |
| [2] | 温浩兴, 许谦, 王娜. 南山26米射电望远镜轨道高差测量及其对指向精度的影响[J]. 天文研究与技术, 2019, 16(2): 158–166 |
| [3] | RANKA T, GARCIA-SANZ M, SYMMES A, et al. Dynamic analysis of the Green Bank Telescope structure and servo system[J]. Journal of Astronomical Telescopes, Instruments and Systems, 2016, 2(1): 014001. DOI: 10.1117/1.JATIS.2.1.014001 |
| [4] | 许谦, 侯晓拯, 王娜. 大口径天线非线性特性动态补偿方法研究[J]. 中国科学:物理学力学天文学, 2019, 49(9): 099504 |
| [5] | 段宝岩. 电子装备机电耦合理论、方法及其应用[M]. 北京: 科学出版社, 2011. |
| [6] | WANG Q M, JIANG P, KONG X. The effects of structural parameter variation on cable force of fast cable-net structure[J]. Advances in Mechanical Engineering, 2015, 6: 912158. |
| [7] | 汪赞, 孔德庆, 陈志平. 大型射电望远镜面形精度测量方法研究综述[J]. 天文研究与技术, 2020, 17(1): 52–59 |
| [8] | KONG D Q, WANG S G, WANG J Q, et al. A new calibration model for pointing a radio telescope that considers nonlinear errors in the azimuth axis[J]. Research in Astronomy and Astrophysics, 2014, 14(6): 733–740. DOI: 10.1088/1674-4527/14/6/011 |
| [9] | RUZE J. Lateral-feed displacement in a paraboloid[J]. IEEE Transactions on Antennas and Propagation, 1965, 13(5): 660–665. DOI: 10.1109/TAP.1965.1138514 |
| [10] | 连培园, 段宝岩, 王伟, 等. 远场反推变形反射面天线馈源调整量[J]. 西安电子科技大学学报, 2014, 41(5): 105–111 |
| [11] | DEVIKA S V, KARKI K, KOTAMRAJU S, et al. A new computation method for pointing accuracy of cassegrain antenna in satellite communication[J]. Journal of Theoretical and Applied Information Technology, 2017, 95(13): 3062–3074. |
| [12] | ZHANG J, HUANG J, LIANG W, et al. A correction method of estimating the pointing error for reflector antenna[J]. Shock and Vibration, 2018, 2018: 3262869. |
| [13] | BAN Y, WANG C S, FENG S F, et al. B-spline surface fitting and simplified GO/PO analysis of subreflector correction for large Cassegrain antenna distortion compensation[J]. Research in Astronomy and Astrophysics, 2018, 18(7): 55–64. |
| [14] | RAHMAN N A, ISLAM M, MISRAN N, et al. Analysis of the BDF using caustics of parabolic reflector antennas[C]//Proceedings of the 2013 Asia-Pacific Microwave Conference. 2013: 1064-1066. |
| [15] | BAARS J W M. The paraboloidal reflector antenna in radio astronomy and communication:theory and practice[M]. Berlin: Springer, 2007. |


