2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
怀柔太阳观测基地是在国际太阳物理界享有高知名度的太阳磁场和速度场观测研究基地和学术研究中心。全日面太阳磁场望远镜是怀柔太阳观测基地的重要设备之一(如图 1),是国家空间天气部门支持的重大课题,于2005年12月实现首光,2006年5月通过验收并投入常规观测[1]。该望远镜主要由Hα望远镜和全日面矢量磁场望远镜两部分组成,旨在通过观测太阳光球大尺度矢量磁场演化和色球活动现象,研究太阳活动爆发的动力学过程和触发机理[2]。目前,该望远镜已经投入观测超过14年,为了保证望远镜的长期稳定运行,提高观测效率,需要对轴系系统进行改造升级。

|
| 图 1 全日面磁场与活动监测望远镜 Fig. 1 Solar Magnetism and the Activity Telescope (SMAT) |
全日面太阳磁场望远镜是赤道式望远镜,部分设计参数如表 1。设计之初安装了光栅钢带码盘作为位置检测元件,基于此元件构建了相应的位置闭环跟踪系统[3]。2012年,码盘发生故障,无法进行望远镜的跟踪导行。望远镜无自动指向功能,需要观测员凭经验通过手柄控制望远镜指向太阳,指向精度不高且效率低。本文针对全日面太阳磁场望远镜进行了轴系升级,将高精度的轴上编码器替代光栅钢带码盘,以更低成本和代价实现望远镜位置检测。使用轴上编码器作为反馈机构,利用高精度的导行系统跟踪太阳并记录太阳实时位置和编码器数值,建立望远镜的坐标体系,实现望远镜的指向功能,可在正常观测时段指向日面中心,提高望远镜的观测效率。
| Full disk vector magnetic field telescope | Full disk Hα observations telescope | |
| Entrance pupil diameter | 100 mm | 200 mm |
| Center wavelength | 532.40 nm | 656.28 nm |
| True field | 33′ × 33′ | 34′ × 34′ |
| Half width | 0.012 5 nm | 0.025 nm |
| Spatial resolution | ≤5″ | ≤2″ |
| Size of CCD | 1 k × 1 k | 2 k × 2 k |
| Tracking accuracy | 1″/30 min (rms) | 1 ″/30 min (rms) |
| Sensitivity of magnetic field | longitudinal component ≤5 Gauss, transverse component is about 100 Gauss | / |
本文第1部分介绍太阳望远镜指向的基本原理,利用该原理实现太阳实时位置的计算,并使用基于大面阵CCD的高精度导行系统不间断跟踪并记录太阳位置[4],利用最小二乘法分段拟合太阳实时位置与绝对式编码器数值,设计指向算法。第2部分,搭建软硬件平台并完成望远镜的升级改造。第3部分,处理并分析实测数据,计算指向误差,最后得出结论。
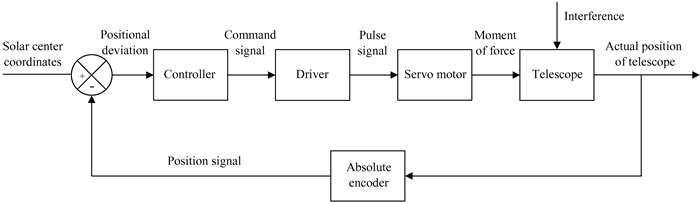
1 太阳望远镜指向基本原理与算法设计指向控制系统是望远镜轴系运动控制的重要子系统,功能是自动将望远镜对准太阳,无需观测人员手动调整。如图 2,首先,建立太阳实时位置和望远镜实时位置模型,依据位置模型,计算望远镜位置和太阳位置之间的差值。然后,根据位置差换算成运动控制系统的脉冲量,将脉冲量发送到轴系控制系统,由轴系控制系统驱动望远镜指向太阳。指向控制系统要求望远镜能快速、准确地指向观测目标,全日面太阳磁场望远镜指向精度的设计指标为1′。
|
| 图 2 系统控制流程图 Fig. 2 System control flowchart |
望远镜指向的目标是日面中心,实现指向首先需要计算实时的日面中心坐标。本文采用文[5]提出的VSOP87行星理论,该方法可以较为准确地计算任意给定时刻太阳系内八大行星相对于太阳的位置分布情况,计算过程较为简便,计算误差在2″以内[5]。
根据该理论对应的地球周期项系数,可以计算:
| $ \begin{array}{*{20}{l}} {l = \sum\limits_{i = 1}^n {{L_i}} {\tau ^i},}\\ {b = \sum\limits_{i = 1}^n {{B_i}} {\tau ^i},}\\ {r = \sum\limits_{i = 1}^n {{R_i}} {\tau ^i},} \end{array} $ | (1) |
其中,τ为当前儒略日距离J2000.0的千年数;l为日心黄经;b为日心黄纬;r为日心距离;Li,Bi,Ri为周期项系数。将日心黄经、日心黄纬转化为地心黄经、地心黄纬后,考虑章动修正量Δλ1和光行差Δλ2可得到视黄经L、视黄纬B:
| $ \begin{array}{*{20}{c}} {L = l + \pi + \Delta {\lambda _1} + \Delta {\lambda _2},}\\ {B = - b.} \end{array} $ | (2) |
通过L和B可计算视赤经、视赤纬:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{tan}}\alpha = \frac{{{\rm{sin}}L{\rm{cos}}e - {\rm{tan}}B{\rm{cos}}e}}{{{\rm{cos}}L}},\\ {\rm{sin}}\delta = {\rm{sin}}B{\rm{cos}}e + {\rm{cos}}B{\rm{sin}}e{\rm{sin}}L, \end{array} $ | (3) |
其中,α为视赤经;δ为视赤纬;e为真黄赤交角。通过α可计算时角t:
| $ t = {S_0} + T + \Delta T - \alpha , $ | (4) |
其中,S0为当天平时0h的恒星时;T为当前的北京时间;ΔT=120°-λ为当地的地理经度与东经120°的差,以时分秒为单位。将赤道坐标转化为地平坐标:
| $ \left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\alpha }&{ - {\rm{sin}}\alpha }&0\\ {{\rm{sin}}\alpha }&{{\rm{cos}}\alpha }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{x^\prime }}\\ {{y^\prime }}\\ {{z^\prime }} \end{array}} \right]. $ | (5) |
通过视赤纬δ和时角t得到方位角A和高度角H:
| $ {{\rm{sin}}H = {\rm{sin}}\phi {\rm{sin}}\delta + {\rm{cos}}\phi {\rm{cos}}\delta {\rm{cos}}t,} $ | (6) |
| $ {{\rm{cos}}A = \frac{{{\rm{sin}}\delta - {\rm{sin}}H{\rm{sin}}\phi }}{{{\rm{cos}}H{\rm{cos}}\phi }}.} $ | (7) |
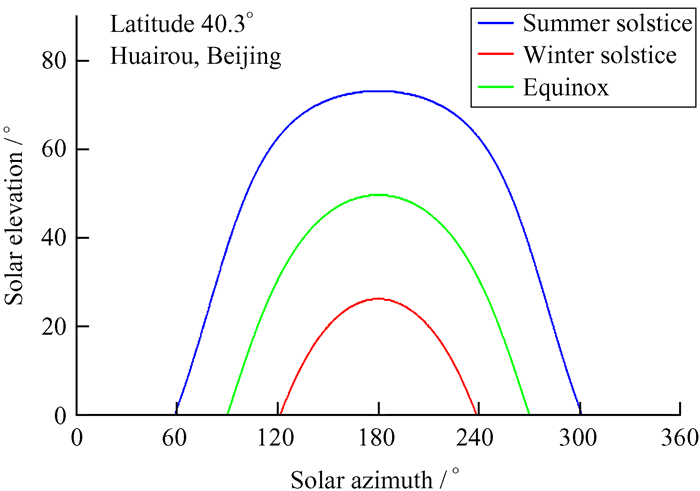
利用上述公式可以实时计算日面中心坐标。图 3为怀柔太阳观测基地不同节气太阳方位角、高度角的变化。
|
| 图 3 怀柔太阳观测基地不同节气太阳方位角、高度角的变化 Fig. 3 Changes in solar azimuth and altitude at different solar termsin HSOS |
通过轴上编码器可实现对电机转动量的测量。电机驱动望远镜机架转动,编码器可以反映望远镜在赤经、赤纬方向的运动情况[6]。通过标定,可以建立编码器数值与望远镜赤经、赤纬方向转动角度的对应关系,从而通过读取编码器数值,建立望远镜坐标,得到望远镜当前位置的具体信息。
利用望远镜自带的刻度盘和陀螺仪测量编码器数值与望远镜的实际位置,可以得到表 2、表 3。多圈数指电机旋转的圈数,即电机旋转了几圈;单圈数指电机旋转后的细分位置(23位的分辨率,每个多圈被细分为8 388 608个位置);总圈数=多圈数× 8 388 608 +单圈数。
| Hour angle | Single-revolution data | Multi-turn data | Total-revolution data of azimuth |
| 06:00 | 5 639 173 | 64 118 | 537 866 406 917 |
| 08:00 | 6 374 936 | 64 586 | 541 793 011 224 |
| 10:00 | 2 614 303 | 65 063 | 545 790 616 607 |
| 12:00 | 4 478 367 | 65 543 | 549 819 012 511 |
| 14:00 | 5 799 792 | 66 020 | 553 821 699 952 |
| 16:00 | 3 612 120 | 66 500 | 557 846 044 120 |
| 18:00 | 6 809 296 | 66 961 | 561 716 389 584 |
| Declination | Single-revolution data | Multi-turn data | Total-revolution data of altitude |
| 30 | 2 660 548 | 65 129 | 537 866 406 917 |
| 20 | 4 427 532 | 65 289 | 541 793 011 224 |
| 10 | 1 283 567 | 65 450 | 545 790 616 607 |
| 0 | 3 586 696 | 65 609 | 549 819 012 511 |
| -10 | 7 425 139 | 65 767 | 553 821 699 952 |
| -20 | 2 753 279 | 65 928 | 557 846 044 120 |
| -30 | 544 914 | 66 089 | 561 716 389 584 |
将时角转化成角度(以正北为0°,顺时针为正),并将时角与对应的方位总圈数进行线性拟合可得到如下关系:
| $ {y_{{\rm{赤经}}}} = {k_1}x + {b_1}, $ | (8) |
其中,k1=132 960 829.93为赤经-圈数转换系数;b1=525 874 647 886.86是与选取的零位相关的截距。拟合后相关系数R2= 0.999 988 12。
在初期调试时发现,由于望远镜本身存在轴系误差,在望远镜通过平衡位置前后,少量数据并不能很好地拟合时角与圈数的关系。为了进一步提高指向精度,根据文[4]提出的利用大面阵CCD采集主望远镜的全日面Hα太阳像进行高精度导行,跟踪太阳并记录太阳的实时位置和编码器数值。通过全天跟踪,利用最小二乘法建立分段拟合关系。
| $ {y_{{\rm{赤经}}}} = \left\{ {\begin{array}{*{20}{l}} {{k_1}x + {b_1}}&{{{90}^\circ } \le x < {{150}^\circ }}\\ {{k_2}x + {b_2}}&{{{150}^\circ } \le x < {{180}^\circ }}\\ {{k_3}x + {b_3}}&{{{180}^\circ } \le x < {{210}^\circ }}\\ {{k_4}x + {b_4}}&{{{210}^\circ } \le x < {{270}^\circ }} \end{array}} \right., $ | (9) |
其中,ki(i=1, 2, 3, 4)为赤经-圈数转换系数;bi(i=1, 2, 3, 4)是与选取的零位相关的截距。拟合后得到:
| $ \begin{array}{*{20}{c}} {}&{{k_1} = 133{\kern 1pt} {\kern 1pt} {\kern 1pt} 989{\kern 1pt} {\kern 1pt} {\kern 1pt} 396.03,}&{}&{{b_1} = 525{\kern 1pt} {\kern 1pt} {\kern 1pt} 635{\kern 1pt} {\kern 1pt} {\kern 1pt} 679{\kern 1pt} {\kern 1pt} 475.37,}\\ {}&{{k_2} = 134{\kern 1pt} {\kern 1pt} {\kern 1pt} 119{\kern 1pt} {\kern 1pt} {\kern 1pt} 324.64,}&{}&{{b_2} = 525{\kern 1pt} {\kern 1pt} {\kern 1pt} 616{\kern 1pt} {\kern 1pt} {\kern 1pt} 255{\kern 1pt} {\kern 1pt} {\kern 1pt} 916.98,}\\ {}&{{k_3} = 134{\kern 1pt} {\kern 1pt} {\kern 1pt} 096{\kern 1pt} {\kern 1pt} {\kern 1pt} 567.09,}&{}&{{b_3} = 525{\kern 1pt} {\kern 1pt} {\kern 1pt} 621{\kern 1pt} {\kern 1pt} {\kern 1pt} 311{\kern 1pt} {\kern 1pt} {\kern 1pt} 109.30,}\\ {}&{{k_4} = 133{\kern 1pt} {\kern 1pt} {\kern 1pt} 934{\kern 1pt} {\kern 1pt} {\kern 1pt} 683.68,}&{}&{{b_4} = 525{\kern 1pt} {\kern 1pt} {\kern 1pt} 656{\kern 1pt} {\kern 1pt} 405{\kern 1pt} {\kern 1pt} {\kern 1pt} 631.19.} \end{array} $ | (10) |
Ri2(i=1, 2, 3, 4)为拟合后的相关系数,经导行数据分段拟合后比原先的相关系数提高了两个数量级。
| $ \begin{array}{*{20}{l}} {R_1^2 = 0.999{\kern 1pt} {\kern 1pt} {\kern 1pt} 999{\kern 1pt} {\kern 1pt} {\kern 1pt} 50,}\\ {R_2^2 = 0.999{\kern 1pt} {\kern 1pt} {\kern 1pt} 999{\kern 1pt} {\kern 1pt} {\kern 1pt} 88,}\\ {R_3^2 = 0.999{\kern 1pt} {\kern 1pt} {\kern 1pt} 999{\kern 1pt} {\kern 1pt} {\kern 1pt} 62,}\\ {R_4^2 = 0.999{\kern 1pt} {\kern 1pt} {\kern 1pt} 999{\kern 1pt} {\kern 1pt} {\kern 1pt} 35.} \end{array} $ | (11) |
将赤纬参数转化成角度(以水平为0°,向上为正),将角度与对应的高度总圈数进行线性拟合得到如下关系:
| $ {y_{{\rm{赤纬}}}} = {k_2}x + {b_2}, $ | (12) |
其中,k2=-398 882 489.78为赤纬-圈数转换系数;b2=549 807 597 273.57是与选取的零位相关的截距。拟合后相关系数R2=0.999 988 12。
1.3 指向的基本算法通过读取时间和地理位置信息,实时计算日面中心坐标。利用轴上编码器计算望远镜位置,并将望远镜位置与日面中心的位置差作为输入。控制器根据
| $ {\rm{驱动器发送脉冲数}} = \frac{{{\rm{日面中心赤经(赤纬)对应总单圈数-望远镜当前赤经(赤纬)总单圈数 }}}}{{{\rm{电机每旋转1单圈输出脉冲数 }}}} $ |
换算为相应的指令信号发送到驱动器,驱动器根据指令将脉冲信号发送到伺服电机,由电机驱动望远镜轴系系统指向太阳。
利用上述原理和算法,可以实现太阳实时位置和望远镜实际位置的计算。下一步需要对全日面磁场与活动监测望远镜进行软硬件改造与升级,结合望远镜的实际情况,完成硬件选型、搭建和调试等工作,并将算法编写成控制软件,通过软硬件平台实现算法功能。
2 轴系系统的改造与升级2012年,全日面太阳磁场望远镜的光栅钢带码盘发生故障,轴系电机也因年代久远无法读取轴上编码器的数值,望远镜无位置检测装置。如果重新安装光栅码盘,需要根据望远镜结构量身定制,更换过程涉及到望远镜光机结构的调整,更换后可能还需要重新对望远镜轴系进行校正。同时,安装新的光栅码盘,还需要研发相应的数据采集系统并确保该系统可以与望远镜控制软件兼容,整个过程需要投入较多的人力物力。为了降低成本并提升兼容性,决定将原电机更换为带有23位绝对编码器的伺服电机,通过集成控制器、驱动器制作新的轴系系统控制箱,实现硬件的改造。同时将编码器数据采集和指向功能集成到全日面望远镜控制系统软件,可以通过该软件实现对轴系系统的全面控制。
2.1 硬件系统的改造在改造升级前,全日面太阳磁场望远镜使用型号为HC-SFS52的三菱电机,额定功率750 W,带有17位增量式编码器,分辨率为131 072 p/rev。为了实现更高精度的位置检测,建立稳定的望远镜坐标,将电机更换为型号MSMF082L1U2M的松下A6伺服电机,驱动器型号为MCDLT35SF。该电机有23位轴上绝对式编码器,分辨率达到8 388 608 p/rev。相比增量式编码器,绝对式编码器的位置由输出代码的读数确定,在一转内每个位置的读数唯一[7]。绝对式编码器构成的绝对式系统接通电源时不需要进行原点复位,可以建立稳定的望远镜坐标系,这对于指向功能的实现极为重要。发生断电或意外移位时,有独立电源的绝对式编码器不会丢失编码信息。
轴上编码器的采集系统集成在伺服电机里,上位机控制器通过RS485或RS232通信可以同时连接赤经、赤纬方向的电机,把位置信息作为串行数据进行读取,将各个数据处理后可以得到两个轴的绝对位置信息[8]。相比于光栅钢带码盘,轴上编码器无需特殊定制,有成熟的通用型产品,成本较低。轴上编码器的数据采集相对简单,不需要额外配置光栅读数头和数据采集卡,也不需要过多考虑安装精度和系统校准等问题。另外,直接更换电机,不会涉及到望远镜结构的位移,不需要对轴系进行重新校正。
更换后新的轴系系统控制箱如图 4,采用型号为ADT-8860的众为兴可编程控制器实现对伺服电机的控制,可读取编码器数值,同时控制箱具备单独的硬限位、手柄控制等接口,可以不经过软件就能实现相应的功能。

|
| 图 4 新轴系系统控制箱 Fig. 4 New shafting system control box |
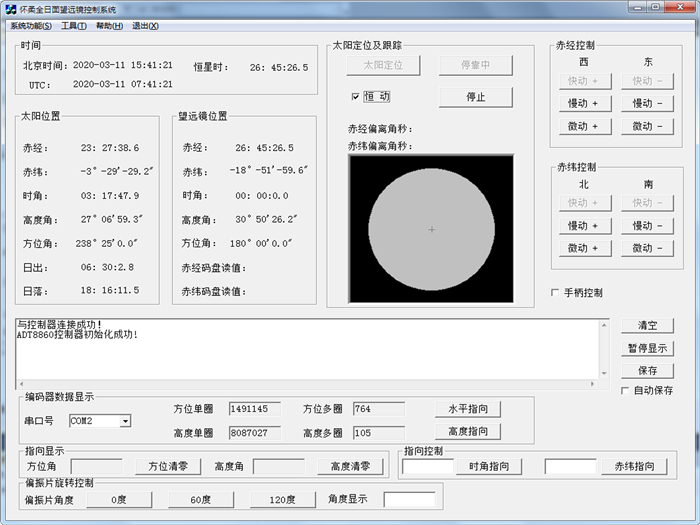
全日面太阳望远镜控制软件(如图 5)是在VS2010开发平台下,使用面向对象的C++语言开发。在原控制系统的基础上,实现了实时读取和显示赤经、赤纬编码器单圈/多圈数值。添加了“方位指向”、“高度指向”等功能,实现日面中心的实时指向,并可通过输入时角、赤纬等参数实现在望远镜轴系允许范围内的指向。
|
| 图 5 全日面太阳望远镜控制系统界面 Fig. 5 Full-disk Solar telescope control system interface |
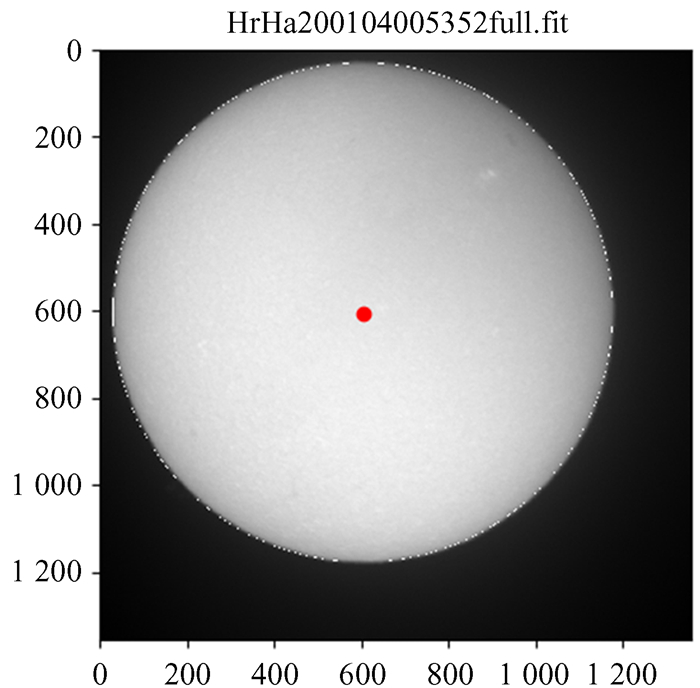
2020年1月4日,对全日面太阳磁场望远镜进行了指向功能的测试。预先设定基准图像(如图 6),从早上8:55到下午15:55,期间每隔15 min进行指向,并保留指向后的全日面Hα太阳像,图 7为每隔60 min指向后的Hα太阳像。通过基于霍夫(Hough)变换的太阳图像质心与半径检测算法对图像进行分析,并与基准图像对比计算误差。通过全天指向得到表 4。
|
| 图 6 基准太阳图像 Fig. 6 The reference H-alpha image |

|
| 图 7 8个时刻指向后的Hα太阳像 Fig. 7 H-alpha images of eight moments afterpointing |
| Time | Right ascension of center coordi-nates/pixel | Right ascension deviation/pixel | Decli-nation of center coordi-nates/pixel | Decli-nation deviation/pixel | Radius/pixel |
| 08:55 | 1 239 | 32 | 1 207 | -4 | 1 147.2 |
| 09:10 | 1 241 | 34 | 1 213 | 2 | 1 146.6 |
| 09:25 | 1 257 | 50 | 1 207 | -4 | 1 146.2 |
| 09:40 | 1 279 | 72 | 1 203 | -8 | 1 146.6 |
| 09:55 | 1 287 | 80 | 1 185 | -26 | 1 147.2 |
| 10:10 | 1 247 | 40 | 1 201 | -10 | 1 149.4 |
| 10:25 | 1 247 | 40 | 1 193 | -18 | 1 148.4 |
| 10:40 | 1 241 | 34 | 1 193 | -18 | 1 148.8 |
| 10:55 | 1 235 | 28 | 1 185 | -26 | 1 149.6 |
| 11:10 | 1 231 | 24 | 1 215 | 4 | 1 146.2 |
| 11:25 | 1 259 | 52 | 1 195 | -16 | 1 147.4 |
| 11:40 | 1 267 | 60 | 1 195 | -16 | 1 150.4 |
| 11:55 | 1 243 | 36 | 1 215 | 4 | 1 146.2 |
| 12:10 | 1 231 | 24 | 1 201 | -10 | 1 148.8 |
| 12:25 | 1 249 | 42 | 1 195 | -16 | 1 147.8 |
| 12:40 | 1 271 | 64 | 1 189 | -22 | 1 148.4 |
| 12:55 | 1 259 | 52 | 1 189 | -22 | 1 150.6 |
| 13:10 | 1 257 | 50 | 1 191 | -20 | 1 149.2 |
| 13:25 | 1 269 | 62 | 1 187 | -24 | 1 150.2 |
| 13:40 | 1 235 | 28 | 1 187 | -24 | 1 146.2 |
| 13:55 | 1 231 | 24 | 1 197 | -14 | 1 151.6 |
| 14:10 | 1 213 | 6 | 1 193 | -18 | 1 150.0 |
| 14:25 | 1 229 | 22 | 1 203 | -8 | 1 149.2 |
| 14:40 | 1 205 | -2 | 1 209 | -2 | 1 149.2 |
| 14:55 | 1 217 | 10 | 1 211 | 0 | 1 150.2 |
| 15:10 | 1 235 | 28 | 1 239 | 28 | 1 148.8 |
| 15:25 | 1 195 | -12 | 1 263 | 52 | 1 145.8 |
| 15:40 | 1 265 | 58 | 1 293 | 82 | 1 144.8 |
| 15:55 | 1 259 | 52 | 1 257 | 46 | 1 149.6 |
经计算,基准图像的(图 6红点)圆心坐标为(1 207.0, 1 211.0)。当天Hα太阳像直径R≈2 296.593 084 pixels,中午12时太阳视直径R′=32′32.01″,可知图 6中1 pixel≈0.849 959″。
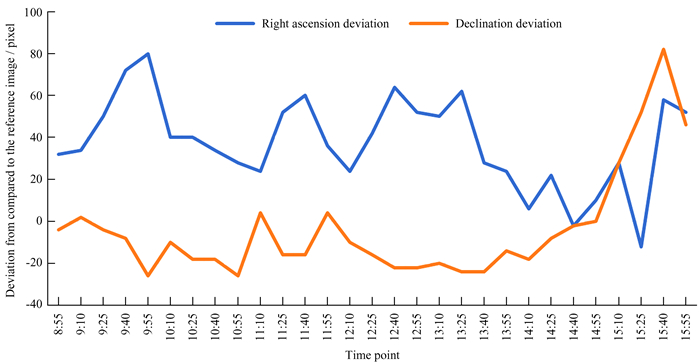
图 8为赤经、赤纬与基准图像的指向偏差。利用
| $ S = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{({x_i} - \mu )}^2}} }}{N}} $ | (13) |
|
| 图 8 不同时间点对应的赤经(赤纬)指向偏差 Fig. 8 Right ascension (declination) pointing deviation at different time points |
可计算指向的标准偏差,SRA=43.169 273 88,SDE=25.281 859 38。经过换算,赤经方向的指向误差约为36.69″,赤纬方向的指向误差约为21.49″,指向精度≤1′,满足指向精度的指标要求。
4 结论本文通过对全日面太阳磁场望远镜轴系系统的升级改造,利用高精度导行系统对太阳进行跟踪,记录太阳实时位置与绝对式编码器数值,并分段进行线性拟合建立指向算法的控制方法。该方法成本低,可移植性强,对赤道式望远镜轴系的兼容性高,可以适用于使用年限较长的望远镜的升级改造。通过实际测试,指向精度优于1′,实现了指向的功能要求,能成功将太阳像引入视场进行导行。
值得一提的是,目前的工作虽然已经达到了全日面太阳磁场望远镜的使用需求,但还有进一步的提升空间,有许多因素可能导致指向误差:望远镜本身轴系误差、指向算法误差、大气蒙气差甚至图像质心与半径检测算法等,后期仍需要通过量化分析建立误差模型,进一步提高指向精度。
致谢: 感谢怀柔太阳观测基地的汪国萍、荆帅等观测人员在研究过程中给予的协助与支持,感谢荀辉、杨潇、张鑫伟、佟立越在研究过程中提供的帮助和宝贵意见,感谢王强提供的基于霍夫变换的太阳图像质心与半径检测算法。
| [1] | 林佳本, 沈洋斌, 朱晓明, 等. 怀柔太阳观测基地全日面磁场自动化观测系统[J]. 天文研究与技术——国家天文台台刊, 2013, 10(4): 392–396 |
| [2] | ZHANG H Q, WANG D G, DENG Y Y, et al. Solar magnetism and the activity telescope at HSOS[J]. Chinese Journal of Astronomy and Astrophysics, 2007, 7(2): 281–288. |
| [3] | 吴春晖, 朱庆生, 周小军. 全日面太阳光学和磁场望远镜的自动跟踪与导行方法[J]. 天文研究与技术——国家天文台台刊, 2007, 4(2): 147–152, 146 |
| [4] | 郭晶晶, 杨云飞, 冯松, 等. 太阳望远镜高精度导行方法[J]. 科学通报, 2016, 61(10): 1112–1120 |
| [5] | 柳光乾.一米红外太阳望远镜控制系统研制[D].昆明: 中国科学院云南天文台, 2011. |
| [6] | 严灵杰.光电望远镜视轴指向及预测技术研究[D].成都: 中国科学院光电技术研究所, 2019. |
| [7] | 程晓莉, 谢剑英, 王林. 绝对式编码器在电机定位中的应用[J]. 控制工程, 2007, 14(5): 548–550 |
| [8] | 柯子博, 晏磊, 王东光. 大气偏振中性点遥感观测系统研制与验证[J]. 影像科学与光化学, 2019, 37(3): 256 |


