2. 中国科学院国家天文台, 北京 100101;
3. 中国科学院大学, 北京 100049
2. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
射电天文研究与一系列国际天文热点问题联系密切,射电望远镜作为高灵敏无线电信号接收设备,可应用于国防、导航授时和遥感遥测等。天文观测中,非常微弱的射频干扰信号会导致观测失败或降低效率,因此,需要尽可能减小射频干扰、降低电磁背景噪声,对于高频观测还需要降低水汽含量,并对其进行持续监测。射电天文使用的大多频段需与其它有源业务共享,在射电天文频段的上下邻频段均存在有源业务,这些业务已经或将来可能对射电天文业务造成干扰,导致部分观测波段、部分观测时间或部分天空覆盖的损失,降低了望远镜的运行效率[1]。射电望远镜台址通过设立电磁环境保护区可减少来自地面的干扰,但由于新业务产生的新发射源,或故障导致发射源的特性改变,尤其是部分移动台站的突然闯入或违规发射,极大地增加望远镜的运行风险。射电望远镜周边存在大量的有源发射业务,由于不同业务具有各自的发射特征,可利用定位技术及时发现射频发射源,这对保护望远镜的有效运行非常重要。
无线定位技术在移动通信、卫星通信、无线传感网络、航空器定位以及无线电管理等无线通信中发挥着至关重要的作用,主要用于紧急救援定位、交通工具导航、无线通信干扰源定位、移动台跟踪、传感器节点定位跟踪、非法无线电发射台站的查找等需要获取位置信息的诸多领域。因获取位置信息的重要性,无线定位技术无处不在,且随着定位算法的不断优化,定位精度的不断提高,应用范围也越来越广。无线定位是利用无线电波的传播特性确定电磁辐射源的位置,是指测量接收机通过对接收的无线电信号的参数进行分析,根据特定的算法获取被测物体的位置信息[2]。测量参数包括传输时间、幅度、相位、电场强度和到达角等。无线定位算法精度高、计算复杂度低,且具有良好的可靠性和鲁棒性,是一种性能优良的定位算法。影响定位精度的主要因素有非视距传播(Non-Line-Of-Sight Propagation, NLOS)、多径干扰、多址干扰、远近效应、噪声、定位算法的选择等。
将无线定位技术应用于射电望远镜射频干扰的查找,通过定位算法及时发现射频干扰源并予以消除或减弱,保护射电望远镜的有效运行,一定程度上降低望远镜的运行风险。
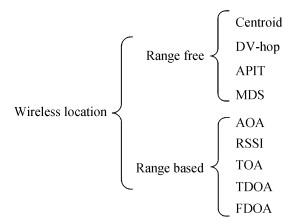
1 测距定位算法无线定位技术按照定位过程中是否进行距离测量分为两类:(1)基于非测距(Range free)的定位,该算法在定位过程中不需要获取距离信息,而是通过节点间的连通性以及节点邻近信息定位,计算复杂度低,成本低,多用于无线传感器网络。基于非测距的算法有:质心算法(Centroid)、DV-hop(Distance-Vector hop)算法、近似三角形内点测试算法(Approximation Point-in-triangulation Test, APIT)、多维尺度法(Multidimensional Scaling, MDS)等[3];(2)基于测距(Range based)的定位:该算法基于节点间的长度和方位角等距离信息进行定位,主要算法有基于到达角(Angle of Arrival, AOA)定位算法、基于接收信号强度(Received Signal Strength Indication, RSSI)定位算法、基于到达时间(Time of Arrival, TOA)定位算法、基于到达时间差(Time Difference of Arrival, TDOA)定位算法[4]、差分多普勒(Frequency Difference of Arrival, FDOA)定位算法等。如图 1。
|
| 图 1 按测距与否无线定位技术分类 Fig. 1 Classification of wireless positioning technologies |
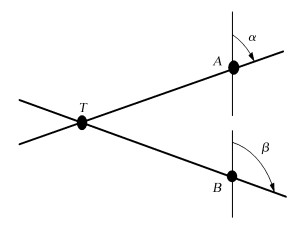
基于到达角定位算法即交叉测向定位法。它通过在不同位置上多次测量方位,测得待定位信号源的方位角,再利用方位线的交汇实现定位或者通过地面固定多站的测角系统所测得的指向线交汇实现定位[5]。定位原理如图 2,A、B为测向监测站,T为待定位的射频信号源。测向监测站根据参考方向,可以测得α与β两个方位角,继而得到两条方位线,方位线交点处即为T的位置。基于到达角定位算法工作原理简单,定位精度受监测站和信号源之间的距离影响较大,距离越大,定位精度越低。多径干扰对基于到达角定位算法影响较大,导致误差变大,定位精度降低。
|
| 图 2 基于到达角定位原理示意图 Fig. 2 Schematic diagram of AOA |
基于到达时间定位算法是指由两个或多个监测站测得待定位信号源发射的信号到达监测站的传播时间,根据
| $ L = c(T + {T_{\rm{n}}}) + \varepsilon $ | (1) |
计算信号源与监测站之间的距离。其中,L为信号源与监测站之间的距离;c为电磁波传播速度,自由空间中取c=3 × 108 m/s;T为信号到达时间;Tn为钟差及传播过程导致的时间误差;ε为未知因素、模型误差等。以各监测站为圆心,监测站到信号源之间的距离为半径作圆,得到两个或者多个圆,这些圆的交点理论上就是待定位信号源的位置[6]。
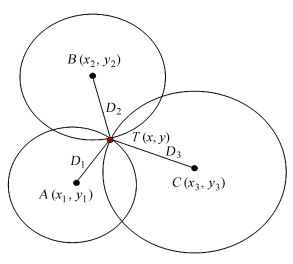
如图 3,有A,B,C 3个监测站对信号源T进行定位,设坐标分别为
| $ \left\{ \begin{array}{l} {(x - {x_1})^2} + {(y - {y_1})^2} = {D_1}^2\\ {(x - {x_2})^2} + {(y - {y_2})^2} = {D_2}^2\\ {(x - {x_3})^2} + {(y - {y_3})^2} = {D_3}^2 \end{array} \right., $ | (2) |
|
| 图 3 基于到达时间定位原理示意图 Fig. 3 Schematic diagram of TOA |
求解方程组,三圆交点处即为信号源的位置。基于到达时间定位算法在网络中实现相对容易,也能达到较高的精度,全球定位系统定位技术主要基于到达时间定位原理。但是基于到达时间定位算法要求各个监测站之间以及监测站与待定位信号源之间在时间上严格同步,微小的误差也会使得定位精度大大降低,时间同步要求高,因此基于到达时间定位系统较为复杂。
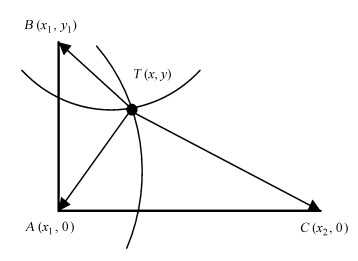
1.3 基于到达时间差定位算法基于到达时间差定位算法通过信号源发出的电磁波信号到达不同监测站的时间差实现对信号源的定位[7]。原理如图 4,A,B,C 3点为监测站,设其坐标分别为
| $ d = \sqrt {{{(x - {x_1})}^2} + {y^2}} - \sqrt {{{(x - {x_2})}^2} + {y^2}} $ | (3) |
|
| 图 4 基于到达时间差定位原理示意图 Fig. 4 Schematic diagram of TDOA |
其中,d为监测站A到信号源T的距离与监测站C到信号源T的距离的差值。根据测得的时间差就可以得到d。将d代入(3)式,可以得到一个关于x和y的双曲线方程。同理,根据监测站A,B与信号源T的距离差,可得另外一个关于x和y的双曲线方程。多个双曲线方程联立方程组求解,双曲线的交点即为信号源位置。基于到达时间差定位算法的计算复杂度低,定位精度高,同步要求较基于到达时间定位算法低,易于实现。
1.4 基于信号到达强度定位算法基于信号到达强度定位算法是监测站通过检测来自待定位信号源的接收信号的强度,一般为场强,再通过选择合适的电波传播损耗模型估算信号源与监测站间的距离,从而确定信号源的位置[8]。传播损耗模型选择不当会对基于信号到达强度定位算法带来很大的误差,户外环境一般选择自由空间传播模型和对数-常态分布模型。自由空间传播模型主要计算视距传播(Line-Of-Sight Propagation, LOS)条件下的接收信号强度,在该模型中,接收端的功率可以表示为
| $ {P_{\rm{r}}}\left( d \right) = \frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}{\lambda ^2}}}{{{{(4\pi )}^2}{d^2}L}}{\rm{ }}, $ | (4) |
其中,Pt为发射机发射功率;Gt为发射天线增益;Gr为接收天线增益;λ为波长;d为接收机到信号源的距离;L为系统损耗因子。
对数-常态分布模型中,接收端的信号强度为
| $ {P_{\rm{r}}} = {P_0} - 10n{\rm{lg}}\left( {\frac{d}{{{d_0}}}} \right) + {N_0}, $ | (5) |
其中,P0为参考场强;d0为参考距离;d为信号传播距离;N0为服从高斯分布的随机噪声;n为衰减因子。
WiFi、蓝牙定位技术是通过接收信号的强度实现的,室内定位也以基于信号到达强度定位算法为主。它具有成本低、设备少、距离远、易获取的特点,但是基于信号到达强度定位算法对电磁信号传播环境的依赖性很大,如果信号传播过程中存在反射、多径传播、非视距传播等问题对定位结果带来很大的误差。因此,在无障碍物的视距传播环境下,算法更加准确,定位精度更高。为尽量避免测量误差,需考虑各监测站的实际要求和几何分布,选择合适的高度布站。规划、建设VHF/UHF频段无线电监测站时,须按国际电信联盟规定的监测站周边障碍物的最小保护间距建站,对已建设和使用的VHF/UHF频段无线电监测站,为减少周边障碍物对测量结果和测向精度的影响,周边障碍物必须满足规定的限制要求[9]。
1.5 差分多普勒定位算法差分多普勒定位算法根据多普勒效应实现定位。当信号源与监测站之间有相对运动时,接收信号的频率或相位与静止不动时接收信号的频率或相位不同。多普勒关系式为
| $ \Delta f = \left( {v/c} \right){\rm{cos}}\alpha {\rm{cos}}\theta f{\rm{ }}, $ | (6) |
其中,v为相对运动速度;c为电磁波的传播速度;f为信号的频率;α为运动方向与信号传播方向的夹角;θ为来波倾角。根据几何关系,由(6)式可知,频差是一个关于信号源位置、监测站位置和监测站运动状态的函数,通过求解可确定多个包含信号源在内的曲面,多个曲面的交点即待定位信号源的位置[10]。
差分多普勒定位算法具有不模糊、定位精度高等优点,但是当信号的多普勒频率分量与信号源的发射频率相比太小时,多普勒频率分量的变化很难被精确测量,导致测量误差增大。因此,差分多普勒定位算法要求测量精度高、成本高,在实际应用中仍然有许多问题。
2 基于数据融合的定位算法无线电通信技术的飞速发展,无线通信业务及台站类型的不断增加,电磁环境日益复杂,对无线定位技术提出了更高的要求。单一的定位算法较难满足高精度定位的需求,多算法数据融合,高精度、高稳定度成为无线定位技术的发展趋势。数据融合的目的是合并或合成多个数据集,成为一个完整的性能更好的数据集[11]。基于到达时间差定位算法定位精度较高,定位系统复杂性低,系统简单,易于组网,基于信号到达强度定位算法简单,成本低,易于实现。本文结合基于到达时间差定位算法与基于信号到达强度定位算法的特点,提出了以基于信号到达强度定位算法测量值为权值,对基于到达时间差定位算法结果进行数据融合的定位算法,消除了基于到达时间差定位算法定位模糊问题的同时,有效提高了定位精度。
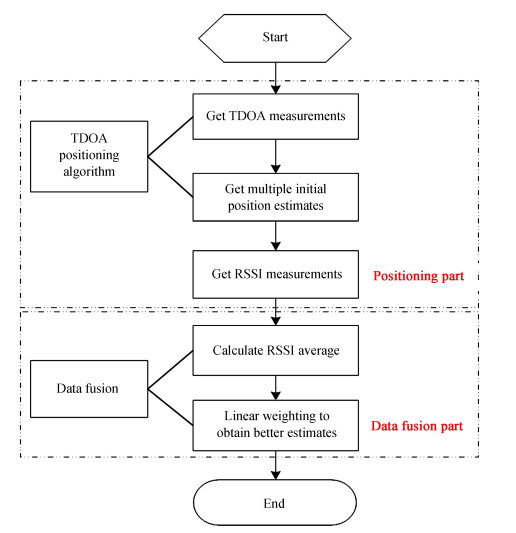
2.1 算法的实现该算法在电磁环境较为良好、信号传播模型较为理想的情况下利用多个监测站联合协同定位,通过对基于到达时间差定位算法和基于信号到达强度定位算法进行数据融合,确定信号源的位置。首先,依次选择两个监测站参与定位,由基于到达时间差定位算法获得多个误差较大的初始位置估计值;其次,以参与定位的两个监测站的接收信号强度基于信号到达强度定位算法值的平均值作为对应初始定位结果的权值,对多个初始位置估计值进行线性加权的数据融合处理,从而获得精度更高的位置估计值。实现过程如图 5。
|
| 图 5 基于到达时间差定位算法和基于信号到达强度定位算法数据融合定位算法示意图 Fig. 5 Schematic diagram of TDOA and RSSI data fusion positioning algorithm |
以5个监测站A,B,C,D,E对待定位信号源T进行基于到达时间差定位为例,各监测站位置坐标分别为
| $ \left\{ \begin{array}{l} \sqrt {{x^2} + {y^2}} - \sqrt {{{({x_2} - x)}^2} + {{({y_2} - y)}^2}} = {d_{12}}\\ \sqrt {{x^2} + {y^2}} - \sqrt {{{({x_3} - x)}^2} + {{({y_3} - y)}^2}} = {d_{13}}\\ \sqrt {{x^2} + {y^2}} - \sqrt {{{({x_4} - x)}^2} + {{({y_4} - y)}^2}} = {d_{14}}\\ \sqrt {{x^2} + {y^2}} - \sqrt {{{({x_5} - x)}^2} + {{({y_5} - y)}^2}} = {d_{15}} \end{array} \right., $ | (7) |
其中,d12, d13, d14, d15可由ti即测量值获得。简化以上方程组,待定位信号源坐标
| $ {D_i} = \sqrt {{{({X_i} - x)}^2} + {{({Y_i} - y)}^2}} , $ | (8) |
| $ D_i^2 = {({X_i} - x)^2} + {({Y_i} - y)^2} = {K_i} - 2{X_i}x - 2{Y_i}y + {x^2} + {y^2}, $ | (9) |
其中,
| $ D_{i,1}^2 + 2{D_{i,1}}{D_1} = {K_i} - 2{X_{i,1}}x - 2{Y_{i,1}}y - {K_1}, $ | (10) |
其中,
(1) 测量各参与定位的监测站接收到的来自信号源的信号强度RSSIi,并将当前参与定位的两个监测站接收信号强度的平均值RAVi作为当前定位获得的初始位置估计值Pi的权值,求所有监测站接收信号强度平均值RAV:
| $ {R_{{\rm{AV}}}} = \frac{{\sum {{R_{{\rm{AV}}i}}} }}{i}, $ | (11) |
(2) 由计算的加权值RAVi对获得的多个初始位置估计值Pi进行对应线性加权,并利用所有监测站接收信号强度平均值RAV进行归一化,最终获得较优的待定位信号源的位置估计值P:
| $ P = \frac{{1/i\left( {\sum {{R_{{\rm{AV}}i}}{P_i}} } \right)}}{{{R_{{\rm{AV}}}}}}. $ | (12) |
本文利用MATLAB仿真工具进行验证。待定位信号源发射正弦信号,电波传播模型为对数-常态分布模型,引入加性高斯白噪声(Additive White Gaussian Noise, AWGN),仿真过程中引入测量误差与噪声误差,相关参数如表 1。
| Parameters | Formula & Value |
| Signal | f(t)=4sin(2π × 3 × 108 t) |
| Frequency | 300 MHz |
| Power | 25 W, 41.94 dBm |
| Measurement error | Uniform Distribution, Mean=0.5 |
| Noise error | Gaussian distribution, N(0, 1) |
以定位结果的均方根误差RMSE作为衡量定位精度的标准:
| $ {R_{{\rm{MSE}}}} = \sqrt {{{\left( {x - X} \right)}^2} + {{\left( {y - Y} \right)}^2}} , $ | (13) |
其中,
| Coordinate | Positioning results without data fusion | Positioning results with data fusion |
| x | 8.610 3 8.625 0 8.486 2 8.624 3 8.563 8 | 8.603 7 |
| y | 6.813 3 6.786 5 6.460 0 6.817 1 6.839 9 | 6.808 6 |
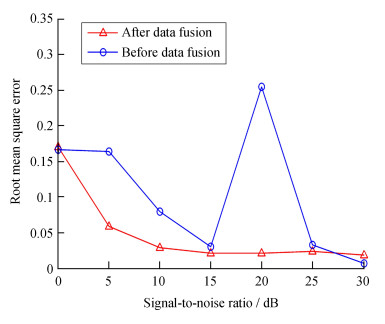
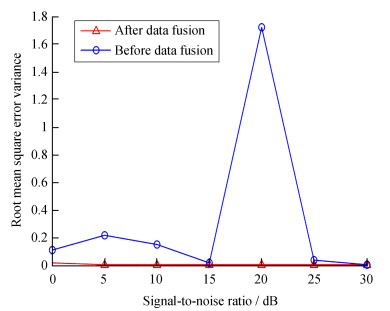
图 6仿真结果表明,经过基于信号到达强度定位算法加权数据融合处理的定位结果均方根误差小于未经过数据融合处理的基于到达时间差定位算法定位结果的均方根误差。表 3为经过仿真的3组定位误差均方差数据的对比,通过比较,经过数据融合处理的基于到达时间差定位算法误差的均方差明显小于未经数据融合的误差的均方差,且数据比较集中,稳定度较高。图 7仿真结果表明,经过数据融合后定位结果的误差方差值较未经过数据融合处理的误差方差值明显减小且平缓。通过多次仿真试验,经过数据融合后的定位误差较未经数据融合单一的基于到达时间差定位算法的误差下降了约20%。综上,说明基于到达时间差定位算法和基于信号到达强度定位算法数据融合的测距无线定位算法精度较高,稳定性较好。
|
| 图 6 定位结果均方根误差比较 Fig. 6 Comparison of root-mean-square error of positioning results |
| Positioning results without data fusion | Positioning results with data fusion |
| 0.340 3 | 0.068 0 |
| 0.189 3 | 0.056 4 |
| 0.169 2 | 0.065 2 |
|
| 图 7 定位结果均方根误差方差比较 Fig. 7 Comparison of root mean square error Variance of positioning results |
本文在分析和研究各测距无线定位算法的基础上,提出了利用多监测站协同、多测距算法融合的无线定位算法,该算法实现了基于到达时间差定位算法与基于信号到达强度定位算法的数据融合,有效消除了基于到达时间差定位算法的定位模糊问题,较好地提高了定位精度,且稳定性强,定位性能更加优良,便于快速准确地及时发现射频干扰源的位置和移动规律,并尽可能在技术或管理层面上予以消除。
| [1] | 李建斌, 彭勃, 刘东亮. 大型射电望远镜电磁环境频谱监测[J]. 电波科学学报, 2015, 30(2): 378–382 |
| [2] | ZHAO J H, WANG D M. Wireless location technology and its application[J]. Engineering Sciences, 2011, 9(4): 32–37. |
| [3] | 孙顺远.无线传感器网络定位算法及应用研究[D].无锡: 江南大学, 2014. |
| [4] | 于天意.复杂环境下的无线定位技术研究[D].北京: 北京交通大学, 2019. |
| [5] | 常娥, 冷卫杰. 工业互联网无线室内定位技术概述[J]. 物联网学报, 2020, 4(1): 1–7 |
| [6] | 夏禹, 张效艇, 王嵘. TOA定位算法的坐标解析优化方法综述[J]. 单片机与嵌入式系统应用, 2019(12): 15–18, 22 |
| [7] | 刘磊, 姚剑, 谢学锋, 等. TDOA无源定位系统的原理与影响因素分析[J]. 无线通信技术, 2017(4): 42–46 |
| [8] | 张珮琪.基于RSSI的室内无线定位与跟踪技术研究[D].西安: 西安电子科技大学, 2016. |
| [9] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. VHF/UHF频段无线电监测站电磁环境保护要求和测试方法: GB/T25003-2010[S/OL]. 2010[2020-04-15]. https://www.jinchutou.com/p-126009065.html. |
| [10] | 季海福, 马利华, 艾国祥, 等. GNSS中结合多普勒频移的DS-R定位新方法[J]. 天文研究与技术——国家天文台台刊, 2014, 11(1): 13–18 |
| [11] | 魏彦飞, 耿建平, 施浒立, 等. 一种新的数据融合方法——广义融合法[J]. 天文研究与技术, 2016, 13(3): 318–325 |


