3C 454.3(红移z=0.859)是一个低光度、低红移,而且有明显剧烈光变的平谱射电类星体。3C 454.3是很受关注的类星体,在光学波段的观测已有很长的历史,研究人员对3C 454.3进行了大量的观测和理论研究。研究表明,3C 454.3的光学波段存在越红越亮的趋势[1]。3C 454.3在伽马波段、光学波段和红外波段都有强烈的光变[2-4],在红外波段的剧烈光变与伽马射线源有关[5]。3C 454.3的光变曲线存在长周期光变,甚至有的耀变体存在十多年的长周期光变[6],长期的观测数据对研究光变周期及其辐射模型有重要意义[7-8]。目前,功率谱方法常用于天体光变周期的讨论,文[9]用功率谱方法计算BL Lac天体S5 0716+714的B, V, R, I波段数据,得到了1.1年的长时标光变。文[10]利用Jurkevich方法和功率谱方法研究了3C 454.3的射电22GHz和37GHz波段存在(1.57±0.12)年及(6.15±0.50)年的周期。光变研究对于揭示耀变体的光变特征和光变机理有重要作用。
1 3C 454.3长期光变曲线通过SMARTS数据库获取了2008年6月至2017年7月3C 454.3的光学和红外波段接近10年的历史光变数据,其中包括光学B, V, R和红外J, K波段,分别有891、855、878、861和752共计4237个观测数据。如果每天可以观测,则光学B, V, R和红外J, K波段的实际观测夜占理论观测夜的覆盖率分别为26.81%、25.72%、26.41%、25.90%和22.62%,平均为25.49%,鲜有如此多波段密集观测的天体。若以天为采样单位,则采样频率约为0.25次/天,依据奈奎斯特(Nyquist)采样定理,采样周期要小于最小信号周期的一半,采样频率应该大于最大信号频率的两倍,奈奎斯特频率约为0.125次/天,可以得知,此观测数据用来计算该天体存在大于8天的光变周期符合奈奎斯特采样定理。
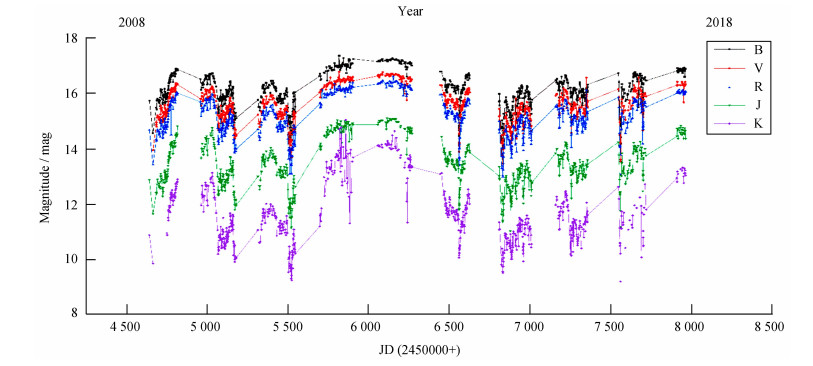
图 1为10年间3C 454.3的B, V, R, J, K波段光变曲线。在2008年6月至2017年7月,该天体B波段的星等平均值为16.108mag,最大值为17.337,最小值为13.964,Δ星等=3.373mag;V波段的星等平均值为15.537mag,最大值为16.756,最小值为13.448,Δ星等=3.308mag;R波段的星等平均值为15.122mag,最大值为16.585,最小值为12.970,Δ星等=3.615mag;J波段的星等平均值为13.419mag,最大值为15.092,最小值为11.012,Δ星等=4.080mag;K波段的星等平均值为11.594mag,最大值为15.017,最小值为9.188,Δ星等=5.829mag。B, V, R, J, K波段的变化量至少有3个星等,见表 1。
|
| 图 1 B, V, R, J, K波段的光变曲线 Fig. 1 Light curve in B, V, R, J and K bands |
| Wavebands | B | V | R | J | K |
| Maximum/mag | 17.337 | 16.756 | 16.585 | 15.092 | 15.017 |
| Minimum/mag | 13.964 | 13.448 | 12.970 | 11.012 | 9.188 |
| Mean/mag | 16.108 | 15.537 | 15.122 | 13.419 | 11.594 |
| Difference/mag | 3.373 | 3.308 | 3.615 | 4.080 | 5.829 |
在光变曲线中,观测数据平均误差约为0.02mag,光变曲线测量值区间平均为Δ星等=4.041mag,信噪比为S=0.5%,信噪比低,在光变曲线和周期分析中未考虑观测误差带来的影响。
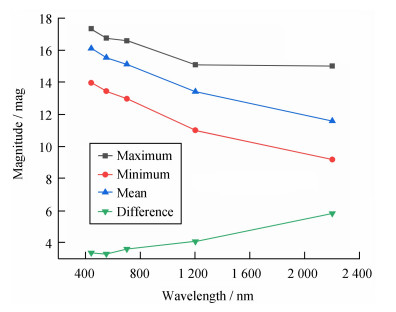
从光变曲线可以看出,3C 454.3天体的光学和红外波段光度在十年间变化十分剧烈。用3C 454.3的B, V, R, J, K波段的中心波长研究其与对应星等最大值、最小值、平均值和差值的关系。图 2显示,在B, V, R, J, K波段中波长越长,对应的星等最大值、最小值和平均值有越低的趋势,然而对应的差值(星等变化量)有越大的趋势。图 1显示,3C 454.3的B, V, R, J, K波段的光变曲线升降走势近乎一致。
|
| 图 2 B, V, R, J, K波段星等最大值、最小值、平均值和差值 Fig. 2 Maximum, minimum, average and difference of magnitude in B, V, R, J and K bands |
在功率谱方法分析中,若存在一个平稳随机信号x(t)的自协方差函数为γx(τ),并满足:
| $ \int_{ - \infty }^\infty {\left| {{\gamma _x}(\tau )} \right|} {\rm{d}}\tau < \infty , $ | (1) |
定义x(t)的功率谱密度函数为γ(τ)的傅里叶变换,即
| $ S_{x}(\omega)=\int_{-\infty}^{\infty} \gamma_{x}(\tau) \mathrm{e}^{-\mathrm{i} \omega \tau} \mathrm{d} \tau, $ | (2) |
则逆傅里叶变换为
| $ \gamma_{x}(\tau)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} S_{x}(\omega) \mathrm{e}^{-\mathrm{i} \omega \tau} \mathrm{d} \omega. $ | (3) |
由自协方差函数的定义有
| $ {\gamma _x}(\tau ) = \mathop {\lim }\limits_{x \to \infty } \frac{1}{{2T}}\int_{ - T}^T {\left[ {x(t) - {\mu _x}} \right]} \left[ {x(t - \tau ) - {\mu _x}} \right]{\rm{d}}\tau . $ | (4) |
由于Sx(ω)dω表示在ω与ω+dω之间信号提供的功率。故Sx(ω)代表功率相对与频率的分布,则称为功率谱函数密度。
对于平稳时间序列{Xn},如它的自协方差序列,γx(k), k=0, 1, 2, …满足
| $ \sum\limits_{k = - \infty }^\infty {\left| {{\gamma _x}(k)} \right|} < \infty , $ | (5) |
则定义{Xn}的自功率谱密度为
| $ {S_x}(\omega ) = \sum\limits_{k = - \infty }^\infty {{\gamma _x}} (k){{\rm{e}}^{ - {\rm{i}}k\Delta t\omega }}, $ | (6) |
其中,Δt为数据采样间隔。自协方差序列γx(k)定义为
| $ {\gamma _x}(k) = \mathop {\lim }\limits_{x \to \infty } \frac{1}{N}{X_n}{X_{n - 1}}. $ | (7) |
功率谱密度函数也可以直接从数字序列的离散傅里叶X(j)利用
| $ I_{n}\left(\omega_{j}\right)=\left(\frac{2 \Delta t}{N}\right)\left|X\left(\omega_{j}\right)\right|^{2} $ | (8) |
获得。
因数字序列的离散傅里叶变换具有周期性,故In(ωj)也具有周期性,所以称In(ωj)为数字序列的周期图估计。可以证明[11],对于一个随机信号
| $ Y_{n}=a \mathrm{e}^{-\mathrm{i} n \omega_{0}}+a_{n}, $ | (9) |
an为平稳正态序列,其功率密度Sa(ω)在ω0处连续,所以Yn的周期图In(ω)必在[-π, π]上ω0附近的某一频率处达到最大值,并且当N很大时有
| $ \mathop {\lim }\limits_{N \to \infty } {I_n}(\omega ) = \left\{ {\begin{array}{*{20}{l}} {\infty , }&{\omega = {\omega _0}}\\ {0, }&{\omega \ne {\omega _0}} \end{array}} \right., $ | (10) |
其中,ω0为信号Yn的固有频率。当N较大时,In(ω)在ω0附近形成一个突起的峰,在其他的频率处,功率谱的密度值较小。根据这种特征,可以寻找信号中的周期成分。当信号含有不止一个周期分量时,In(ω)出现多个极大值。为了判别真伪周期,需要根据周期图极大对应的频率值,利用最小二乘法求出相对应各频率的周期分量的振幅比较大小。
SMARTS数据中的采样数据并非均匀采样时间序列,用功率谱方法计算3C 454.3的光变周期时,对光变数据的空白处进行了相邻数据平均值插值处理。
以上为功率谱方法测量周期的基本原理,对于耀变体长周期光变研究可靠性的理论见文[9]。
2.2 结果通过功率谱方法计算,得到了3C 454.3的B, V, R, J, K波段功率谱图,图 3显示了2个主要的频率峰值。
|
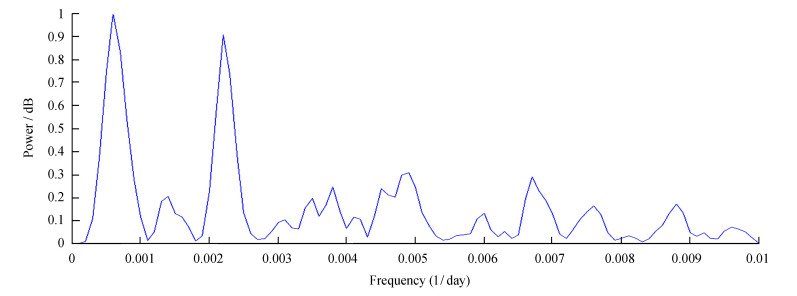
| 图 3 B波段功率谱图 Fig. 3 The power spectrum figure in B band |
从B波段功率谱图看,存在周期有454.5和1666.7天,分别对应1.25年和4.57年。峰值频率为0.00060(1/day)的半高宽为0.00035;峰值频率为0.00220(1/day)的半高宽为0.00030,如图 3。
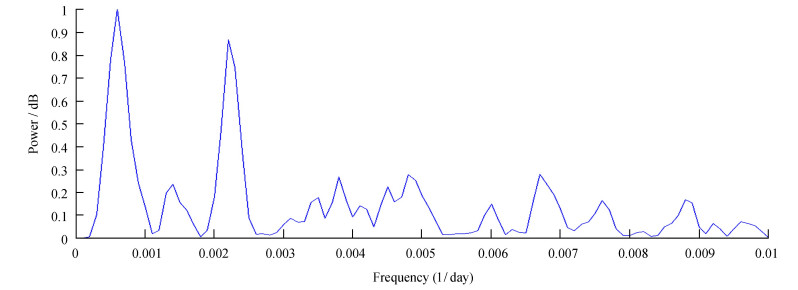
从V波段功率谱图看(图 4),存在周期有454.5和1666.7天,分别对应1.25年和4.57年。峰值频率为0.00060(1/day)的半高宽为0.00038;峰值频率为0.00220(1/day)的半高宽为0.00032。
|
| 图 4 V波段功率谱图 Fig. 4 The power spectrum figure in V band |
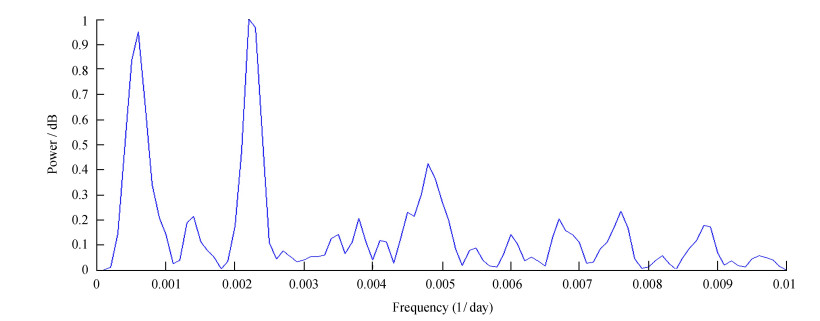
从R波段功率谱图看(图 5),存在周期有454.5和1666.7天,分别对应1.25年和4.57年。峰值频率为0.00060(1/day)的半高宽为0.00035;峰值频率为0.00220(1/day)的半高宽为0.00030。
|
| 图 5 R波段功率谱图 Fig. 5 The power spectrum figure in R band |
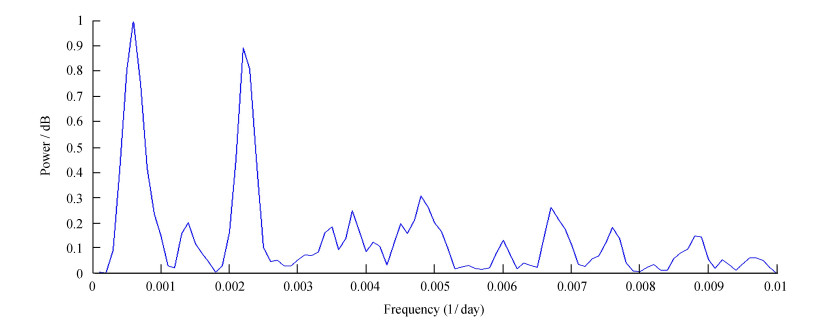
从J波段功率谱图看(图 6),存在周期有454.5和1666.7天,分别对应1.25年和4.57年。峰值频率为0.00060(1/day)的半高宽为0.00036;峰值频率为0.00220(1/day)的半高宽为0.00030。
|
| 图 6 J波段功率谱图 Fig. 6 The power spectrum figure in J band |
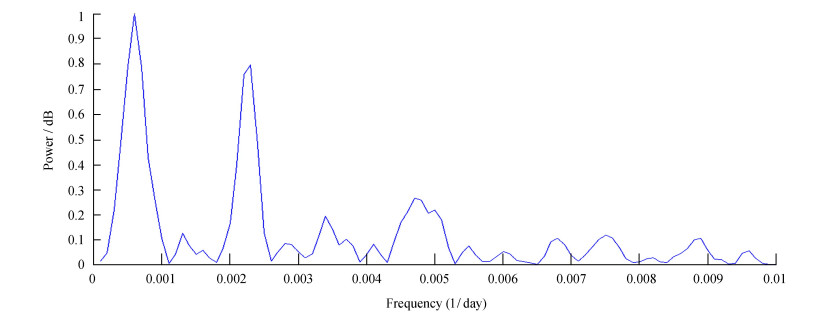
从K波段功率谱图看(图 7),存在周期有434.8和1666.7天,分别对应1.19年和4.57年。峰值频率为0.00060(1/day)的半高宽为0.00038;峰值频率为0.00230(1/day)的半高宽为0.00033。
|
| 图 7 K波段功率谱图 Fig. 7 The power spectrum figure in K band |
各个波段的功率谱图峰值频率及其半高全宽见表 2。通过计算得到3C 454.3在光学和红外波段都存在2个光变周期,分别为1.25年和4.57年。
| Wavebands | B | V | R | J | K |
| First peak frequency | 0.00060 | 0.00060 | 0.00060 | 0.00060 | 0.00060 |
| FWHM of first peak | 0.00035 | 0.00038 | 0.00035 | 0.00036 | 0.00038 |
| Second peak frequency | 0.00220 | 0.00220 | 0.00220 | 0.00220 | 0.00230 |
| FWHM of second peak | 0.00030 | 0.00032 | 0.00030 | 0.00030 | 0.00033 |
图 1显示,在3C 454.3的B, V, R, J, K 5个波段中,历史光变曲线变化近乎一致,图 3~图 7显示功率谱图大致相同,这有可能产生于3C 454.3在光学和红外波段的光度变化根本上有着一定的关系。
根据图 2,在B, V, R, J, K波段中的波长越长,对应的星等最大值、最小值和平均值有越低的趋势,然而对应的差值有变大的趋势。星等越低,光度也越亮,这暗示着在大部分时间,红外波段比光学波段更为明亮。3C 454.3光度变化时,红外波段比光学波段较为剧烈。文[1]研究了3C 454.3在2006~2011年光学波段明显存在越红越亮的趋势,这个趋势到红外J、K波段也适用。
根据表 2,各波段都显示出2个显著周期,频率为0.00060(1/day)的周期在5个波段完全一致。而K波段434.8的周期不同于其余4个波段,通过计算并查表可得,各波段该周期均值为450.6天,周期置信度为0.95的置信区间为[442.9, 458.3]天,即450.6±7.72天,区间可表述为[1.21, 1.26]年,说明1.25年的周期具有较高的置信水平,可以作为3C 454.3的主要周期。
半高全宽较小的峰值对应的误差相对较小,因此峰值频率为0.0022(1/day)的周期比峰值频率为0.0006(1/day)的周期更为显著;前者对应的周期为1.25年,后者对应的周期为4.57年。1.25年的周期与文[12]在射电波段21.7GHz计算得到的1.2年周期光变大致相符,因此1.25年的周期可以认为3C 454.3的显周期,其光变曲线主要由1.25年的周期导致。在光学波段、红外波段和射电波段的周期相同,可以认为3C 454.3的光度变化及其周期特征现象在光学、红外和射电波段具一定的关系。
本文使用功率谱方法得到的周期有1.25年和4.57年,其中4.57年的周期因为受观测时间和观测数据的影响,其半高宽略大,误差相对较大,与其真实周期可能有偏差,视为1.25年周期的叠加。
4 结论对3C 454.3在B, V, R, J, K波段的光变比较分析显示,3C 454.3的红外波段的光度比光学波段更为明亮,红外波段的光度变化比光学波段更为剧烈。
用功率谱方法对平谱射电类星体3C 454.3中B, V, R, J, K波段的光变曲线进行研究,结果表明,该天体在光学、红外波段存在光变主周期为1.25年,4.57年的周期为1.25年周期的叠加。由于相对以前的研究,信号采样是中长周期光变的研究障碍而不可避免,本文在利用最新(2008~2017年)SMARTS计划的观测基础上,首次利用功率谱方法计算3C 454.3的光学红外B, V, R, J, K波段周期,获得了相对准确的结果。在光学、红外和射电波段的周期相同,可以认为3C 454.3的光度变化及其周期特征现象在光学、红外和射电波段具有一定的关系。
| [1] | FAN X L, LI S K, LIAO N H, et al. Optical and gamma-ray variability behaviors of 3C 454.3 from 2006 to 2011[J]. The Astrophysical Journal, 2018, 856: 80–88. DOI: 10.3847/1538-4357/aab09d |
| [2] | WEAVER Z R, BALONEK T J. The dramatic June 2016 optical outburst and micro-variability of the blazar 3C 454.3[C]//Proceedings of the American Astronomical Society Meeting. 2017. |
| [3] | TACHIBANA Y, KAWAI N, PIKE S. A correlation between optical, X-ray, and gamma-ray variations in blazar 3C 454.3[C]//Proceedings of the 5th Fermi Symposium. 2015. |
| [4] | HAGEN-THORN V A, EFIMOVA N V, LARIONOV V M, et al. Color variations of the blazar 3C 454.3 in 2004-2006[J]. Astronomy Reports, 2009, 53(6): 510–518. DOI: 10.1134/S1063772909060031 |
| [5] | BONNING E W, BAILYN C, URRY C M, et al. Correlated variability in the blazar 3C 454.3[J]. The Astrophysical Journal Letters, 2009, 697(2): L81–L85. DOI: 10.1088/0004-637X/697/2/L81 |
| [6] | ZHANG H J, ZHAO G, ZHANG X, et al. Long-term optical spectra variability of quasar 3C 273[C]//Proceedings of the Astronomical Society of the Pacific Conference Series. 2009: 388-390. |
| [7] | 余莲, 张雄, 王文广, 等. 蝎虎天体PKS 0735+178的光变特性分析[J]. 天文研究与技术, 2018, 15(1): 10–16 |
| [8] | 米立功, 崔朗, 胡开宇. 59个耀变体的15.3GHz光变周期分析[J]. 天文研究与技术, 2015, 12(4): 410–416 DOI: 10.3969/j.issn.1672-7673.2015.04.004 |
| [9] | 张皓晶, 张雄. BL Lac天体S50716+714的光变周期特性研究[J]. 物理学报, 2007, 56(7): 4305–4311 DOI: 10.3321/j.issn:1000-3290.2007.07.110 |
| [10] | LI H Z, XIE G Z, ZHOU S B, et al. A periodicity analysis of the light curve of 3C 454.3[J]. Chinese Journal of Astronomy and Astrophysics, 2006, 6: 421–429. DOI: 10.1088/1009-9271/6/4/04 |
| [11] | 丁月蓉, 郑大伟. 天文测量数据的处理方法[M]. 南京: 南京大学出版社, 1980: 320-327. |
| [12] | GORSHKOV A G, IPATOV A V, IPATOVA I A, et al. Long-term and rapid radio variability of the blazar 3C 454.3 in 2010-2017[J]. Astronomy Reports, 2018, 62: 183–199. DOI: 10.1134/S1063772918030046 |



