2. 地理学国家级实验教学示范中心, 陕西 西安 710119
2. National Experiment and Teaching Demonstration Center for Geography, Xi'an 710119, China
撞击坑不仅是月球表面最典型的形貌构造单元,也是月球形态特征演化和发育研究的直接切入点[1]。因月表几乎没有大气层保护,且无风、水的侵蚀,地质活动微弱,所以撞击坑得以较完整地保存[2]。撞击坑的形成过程、形态特征及空间分布等从不同方面为研究月球演化历史提供了线索和方法[3]。撞击坑坑唇是撞击坑形态特征表达的最直观载体,是月表撞击坑形态模拟重建的基本单元。通过对撞击坑坑唇形态特征及其量化指标关系的研究,不仅可以还原撞击坑的形成过程,还可以进一步推知月球的地质特征、物质组成,揭示演化过程等[4]。构建月表撞击坑形态量化指标因子模型,探索不同指标因子间的关联特征,实现指标因子的量化关系模拟,对于月表撞击坑形态表达和发育演化有积极的理论意义和实践意义[5]。
将撞击坑深度与直径之比作为撞击坑相对年龄的判定依据,撞击坑可以分为新鲜、年轻、成熟和老年4类[6]。文[7]基于行星撞击坑分形及分维数理论,对月表撞击坑数目与直径之间的关系进行了深入研究,揭示了撞击坑月表地质年龄复杂的量化本质,实现地貌形态量化研究从简单的撞击坑直径向分维数的转变。文[8]研究了雨海地区粗糙度及其与岩性的关系,通过赫斯特(Hurst)指数的计算,分析了月表粗糙度分布特征及其与岩性和地质年龄的关系,进一步探索了火山作用对月表粗糙度的影响。文[9]基于撞击坑数理统计和比较分析,从撞击坑的位置、大小、形状、坡度、方向、中央峰、辐射纹等7个视角52个小类指标,构建了月表撞击坑全关系型数据库,实现对撞击坑数据的存储、检索、处理和应用。文[10]选择坑唇等效半径、坑底等效半径和撞击坑深度3个参数进行统计和聚类分析,以此研究撞击坑形貌与3个参数复杂程度的关系。文[11]基于月表撞击坑的形态学特征构建了描述指标体系,对其分别进行地理学意义的描述和计算方式的表达,进一步构建了撞击坑个体描述指标和群体性描述指标体系,实现了月表撞击坑形态发育的体系性评价。
在月表形貌学和数字地形分析中,地形因子的表达虽已经从定性描述转变为定量表达,但传统的地形因子和特定的描述指标受限于提取过程和方式,仅对月表撞击坑形态进行综合概括和单一刻画[12-13]。此外,基于数字地形信息挖掘的多因子联合定量表达以及量化关系研究,是反映形态特征与发育演化,揭示多因子与自然系统之间规律的重要内容。
本文以月表撞击坑为基本单元,以月球勘测轨道器相机(Lunar Reconnaissance Orbiter Camera, LROC)的100 m高分辨率数字高程模型为数据基础,在全月选择1 407个不同类型的撞击坑,它们能科学、全面、准确地刻画撞击坑形态特征与地形信息,探索描述撞击坑形态特征指标因子间的关联性和表征意义,构建基于多因子的量化关系模型,以揭示地形因子信息与撞击坑形貌发育的内在联系。
1 数据来源与研究方法 1.1 研究区及实验样区撞击坑的形成及发育过程受诸多不确定因素的影响,如陨石撞击方向、力度、月表岩性与月壤厚度等,因此,在撞击坑形态指标因子的计算中,撞击坑的选择尤为重要,对于撞击坑类型的划分,已总结出几种学界较为权威的分类方案,本文以文[14]对月表撞击坑类型的划分作为研究基础。基于类型全面、发育典型等原则选择坑体结构较为完整的撞击坑作为研究数据,如图 1。

|
| 图 1 选择的撞击坑在全月球分布情况 Fig. 1 The distribution of the slected craters on the lunar surface |
基于现有资料,本文依据数据完整性、实验科学性和数据可获取性等原则,结合撞击坑面积大小、撞击坑之间的空间位置关系、撞击坑的形态发育特征等,在月表选择1 407个撞击坑,其中包括离散型撞击坑、群聚型坑连坑、群聚型坑套坑以及边缘退化型撞击坑4大类型。具体类型如表 1。
月球勘测轨道飞行器(Lunar Reconnaissance Orbiter, LRO)获取的100 m分辨率数字高程模型数据,基于基本地形因子和撞击坑形态特征实现撞击坑地形结构的划分,作为研究的数据基础。
1.3 实验流程首先通过对已建立的撞击坑形态指标体系进行总结,结合撞击坑形貌形态特征表达和发育演化机理,有效地实现撞击坑地形因子的遴选。然后对1 407个撞击坑地形因子和指标进行提取并量化统计。在此基础上,利用数理统计与地理建模的方法,重点探讨撞击坑地形因子间的关联性,进一步实现基于多因子的量化关系模拟。
2 结果与分析 2.1 指标因子的选择对于月表撞击坑的发育而言,坑唇是撞击坑形态特征与演化过程的基本表征,反映月表撞击坑退化发育的演变过程。因此,本文基于已建立的撞击坑形态指标体系[14],从撞击坑尺寸规模、形态发育和特征统计等方面对指标进行剖析,兼顾蕴含的地学意义和指标依赖关系,科学合理地遴选出能够反映撞击坑形态特征与发育特征的指标因子,用作构建量化模型的基础。选取的指标因子见表 2,这些指标从坡度、高程以及二三维空间形态等多重视角出发,重点刻画撞击坑的基本形态,蕴含丰富的撞击坑形态发育特征信息,撞击坑指标获取过程见图 2。
| 指标 | 定义 | 计算方法 | 指标意义 | 图例说明 |
| 直径 | 撞击坑坑唇直径 | 反映撞击坑最终状态下的直径 | 图 2(a) | |
| 圆度 | 撞击坑接近圆的程度 | C=4πA/P2 | 反映撞击坑边缘的复杂性 | |
| 深度 | 撞击坑坑唇最高点与月坑底最低点之间的高程差 | H=HKCMAX-HKDMIN | 反映撞击坑最后状态下的深度 | 图 2(b) |
| 体积 | 由撞击体撞击形成的凹坑体积 | V=0.5AR-SUMcellsize | 反映撞击坑体积的大小 | |
| 体态比 | 撞击坑坑唇最小外界矩形的宽度与长度之比 | Rp=W/L | 反映撞击坑的狭窄程度 | 图 2(c) |
| 深径比 | 撞击坑深度与直径之比 | H/D | 反映撞击坑的发育程度 | |
| 坑唇起伏度 | 撞击坑坑唇最大高程与最低高程之差 | R=HKCMAX-HKDMIN | 反映撞击坑在月表垂直方向的起伏程度 | 图 2(b) |
| 坑壁平均坡度 | 撞击坑内壁的平均坡度 | ArcGIS Slope | 反映撞击坑内壁的陡峭程度 | |
| 注:S为撞击坑的坑口面积;P为撞击坑坑唇周长;HKCMAX和HKDMIN分别为撞击坑坑唇最高点和撞击坑坑底最低点;SUM为坑壁和坑底向下对应的体积;cellsize为数字高程模型数据的空间分辨率;W为撞击坑坑唇最小外接矩形的宽;L为坑唇最小外接矩形的长。 Note: S is the area of the crater pithead, P is the perimeter of the impact crater, HKCMAX and HKDMIN respectively indicate the highest point of the impact crater rim and the lowest point of the crater bottom, and SUM bounded by the crater bottom and walls, cellsize is the spatial resolution of the DEM data, W is the width of the minimum bounding rectangle of the impact crater rim, and L is the length of the minimum bounding rectangle of the impact crater rim. | ||||
|
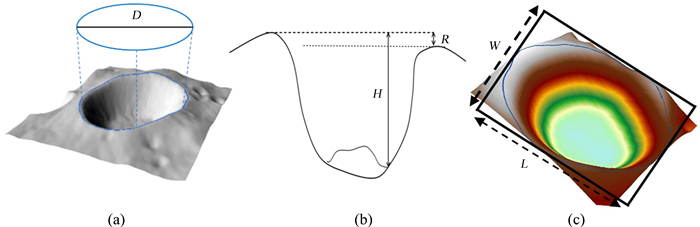
| 图 2 撞击坑形态参数指标的获取过程。(a)直径的获取过程;(b)深度与坑唇起伏度的获取过程;(c)体态比的获取过程 Fig. 2 Acquisition process of crater morphological indices. (a) acquisition process of diameter; (b) acquisition process of depth and rim fluctuation; (c) acquisition process of posture ratio |
在研究中,首先从刻画月表撞击坑特征和自然表达效果角度对现有撞击坑坑唇形态提取算法进行对比。结果发现,基于地形分析方法的撞击坑坑唇的提取算法,对一定尺度级别的月表撞击坑特征要素表达方法具有一定的优势[15]。此外,通过对月表撞击坑形态的目视解译和撞击坑坑唇形态提取算法的本质认识发现,目前大多撞击坑坑唇形态的提取算法对其识别准确度都受实验样区选择的限制,且伴随有因窗口平滑而造成的细节简化问题,造成撞击坑真实坑唇信息的丢失,而基于目视识别的撞击坑坑唇形态的提取方式对于撞击坑特征的反映具有较高的可靠性,提取结果与月表撞击坑自然坑唇状态吻合最好。在1 407个撞击坑样本的基础上,利用数字高程模型数据,采用目视识别的方法进行撞击坑坑唇形态识别,以此提取撞击坑坑唇线。然后根据撞击坑类型划分结果,对已选择的8个地形指标因子进行量化计算,各项指标计算结果见表 3。
| 类型 | 直径 D/km | 深度 H/km | 体积 V/km3 | 圆度 C | 体态比 Rp | 深径比 H/D | 坑壁坡度 S/° |
| 1 | 12.396 | 2.313 | 167.554 | 0.972 8 | 1.156 4 | 0.186 7 | 21.40 |
| 2 | 11.395 | 1.919 | 161.681 | 0.935 6 | 1.027 4 | 0.171 4 | 17.34 |
| 3 | 31.199 | 3.346 | 2 710.198 | 0.952 2 | 1.128 9 | 0.112 2 | 17.28 |
| 4 | 47.936 | 2.135 | 1 226.035 | 0.945 5 | 0.883 8 | 0.077 1 | 13.48 |
| 5 | 29.659 | 2.721 | 1 937.222 | 0.898 0 | 0.890 1 | 0.113 6 | 14.09 |
| 6 | 59.432 | 3.921 | 8 366.350 | 0.909 2 | 0.877 1 | 0.075 0 | 13.57 |
| 注:1代表新鲜离散型撞击坑;2代表新鲜坑连坑;3代表新鲜坑套坑;4代表退化离散型撞击坑;5代表退化坑连坑;6代表退化坑套坑。 Note: 1 is the fresh dispersed craters; 2 is the fresh connected craters; 3 is the fresh contained craters; 4 is the dispersed craters of degradation; 5 is the connected craters of degradation; 6 is the contained craters of degradation. | |||||||
从表 3可以看出,不同类型撞击坑形态指标之间的差异性,新鲜撞击坑的圆度平均大于退化撞击坑,说明新鲜撞击坑的坑口接近圆形,在新鲜撞击坑中,坑连坑圆度值小于坑套坑,坑连坑的坑唇形态由于相互的挤压发生较大的变化,新鲜撞击坑中的离散型撞击坑深径比是退化离散型撞击坑的两倍多,退化撞击坑由于坑底被熔岩填充或坑壁发生块体移动,使得撞击坑的深度变化远快于直径变化,因此,新鲜撞击坑的深径比整体大于退化撞击坑的深径比。说明描述撞击坑不同形态特征的指标之间存在相互影响,解析清楚指标间的相关性是构建撞击坑综合模型的基础。
2.3 指标关联性分析撞击坑的形态特征是一个复杂的渐变系统,虽然其内部各要素之间有概念描述和量化表达的差异性,但各要素之间普遍存在联系而绝非孤立的表达,选取有效的地形因子指标进行关联性分析并实现撞击坑形态的发育模拟是本文的重点。
关联性分析即相关性分析,是揭示描述地理特征的各因子之间相关关系的密切程度,主要通过相关系数反映。本文通过选择的撞击坑计算各项指标,进而进行指标因子的单相、偏相关分析,以探讨形态指标因子两两之间的量化关系。各项形态指标单相关系数计算结果如表 4。
| 直径 | 深度 | 体积 | 圆度 | 体态比 | 深径比 | 坑壁坡度 | 坑唇起伏度 | |
| 直径 | 1 | 0.474 | 0.510 | -0.256 | -0.209 | -0.535 | -0.167 | 0.415 |
| 深度 | 0.474 | 1 | 0.497 | -0.212 | 0.014 | 0.025 | 0.260 | 0.723 |
| 体积 | 0.510 | 0.497 | 1 | -0.266 | -0.094 | -0.259 | -0.135 | 0.431 |
| 圆度 | -0.256 | -0.212 | -0.266 | 1 | 0.180 | 0.328 | 0.270 | -0.305 |
| 体态比 | -0.209 | 0.014 | -0.094 | 0.180 | 1 | 0.317 | 0.311 | -0.179 |
| 深径比 | -0.535 | 0.025 | -0.259 | 0.328 | 0.317 | 1 | 0.666 | -0.108 |
| 坑壁坡度 | -0.167 | 0.260 | -0.135 | 0.270 | 0.311 | 0.666 | 1 | -0.080 |
| 坑唇起伏度 | 0.415 | 0.723 | 0.431 | -0.305 | -0.179 | -0.108 | -0.080 | 1 |
| 注:样本为1 407个,相关性显著程度在0.01置信度水平下。 Note: the number of sample is 1407. Significant correlation at a confidence level of 0.01. | ||||||||
通过单因子相关性分析结果可知,直径与深径比有较好的相关性,深度与坑唇起伏度之间的相关性较好,深径比与坑壁坡度间也存在较好的相关性,这说明撞击坑形态指标之间普遍存在一定程度的联系,且此种联系在多因子之间表现得更为复杂,有必要进一步进行多因子综合相关性分析。对选择的8个地形因子指标进行主成分分析,从而确定最能表达撞击坑形态的因子及组合,通过多次试验发现,做4次主成分分析是合理的,计算结果如表 5、表 6。
| 指标 | 主成分 | |||
| 1 | 2 | 3 | 4 | |
| 直径 | 0.784 | 0.049 | 0.289 | 0.288 |
| 深度 | 0.613 | 0.705 | -0.059 | 0.025 |
| 体积 | 0.706 | 0.237 | 0.273 | 0.055 |
| 圆度 | -0.559 | 0.146 | 0.204 | 0.733 |
| 体态比 | -0.386 | 0.404 | 0.693 | -0.393 |
| 深径比 | -0.620 | 0.630 | -0.273 | -0.074 |
| 坑壁坡度 | -0.404 | 0.767 | -0.072 | 0.095 |
| 坑唇起伏度 | 0.707 | 0.425 | -0.283 | -0.044 |
| 成分 | 初始特征值 | 提取平方和载入 | |||||
| 合计 | 方差的百分比/% | 累计百分比/% | 合计 | 方差的百分比/% | 累计百分比/% | ||
| 1 | 2.997 | 37.466 | 37.466 | 2.997 | 37.466 | 37.466 | |
| 2 | 1.906 | 23.824 | 61.290 | 1.906 | 23.824 | 61.290 | |
| 3 | 0.843 | 10.542 | 71.833 | 0.843 | 10.542 | 71.833 | |
| 4 | 0.795 | 9.937 | 81.770 | 0.795 | 9.937 | 81.770 | |
| 5 | 0.560 | 6.994 | 88.764 | ||||
| 6 | 0.527 | 6.584 | 95.348 | ||||
| 7 | 0.216 | 2.697 | 98.045 | ||||
| 8 | 0.156 | 1.955 | 100.000 | ||||
从表 5可以看出,第1主成分在撞击坑的体积、直径、坑唇起伏度和深度上都具有较大的正载荷,而只有深径比在第1主成分内有较好的负载荷,以上5个指标从撞击坑的规模大小及发育程度的视角来表征撞击坑的形态特征,因此,第1主成分可以看做是撞击坑规模及其发育的代表。第2主成分与撞击坑坑壁平均坡度和深径比都有较大的正相关,这两个指标与撞击坑的坑唇或坑壁发育密切相关,这说明第2主成分是从撞击坑坑唇和坑壁发育状况视角表达撞击坑的形态特征。虽然在第3主成分中体态比的相关性得分较低,但体态比在表征撞击坑坑唇形态的狭窄程度上有独特优势,因此,在描述撞击坑形态特征时,体态比因子不可或缺。在第4主成分中,圆度因子具有较大的载荷,而圆度从撞击坑的坑唇复杂程度这一独特视角表征撞击坑的形态特征,因此对撞击坑形态特征的描述,圆度是具有独特优势的指标因子。
从表 6不难发现,选择4个主成分,其累计贡献率达81.77%,保障了对后面撞击坑形态特征发育指标的线性模拟。而从形态指标主成分分析的总方差解释表中也可以看出,第3和第4主成分的贡献率虽不及第1和第2主成分,但第3和第4主成分对于撞击坑形态的影响不可忽略。在第1主成分中,影响撞击坑规模的指标因子众多,而在学界,深径比作为撞击坑发育表征的二维指标因子,对于撞击坑相对年龄的判断有很好的指示作用[15]。它与众多因子之间有较多的联系,并非单一化的关联关系。本文基于多因子关联性分析,旨在寻求撞击坑形态发育与其他形态指标之间的量化关系,考虑到多因子综合分析的复杂性,可以将深径比作为一个主变量,通过多层次探索在多因子相互影响下双变量之间的关联关系的方法,这种方法是通过控制变量的方式不断增加控制因变量,进而实现各因子间关联性分析。各级偏相关结果如表 7。
| 控制变量 | 深径比 | 直径 | 体积 | 圆度 | 体态比 | 坑壁坡度 | |
| 深径比 | 1.000 | 0.019 | 0.234 | 0.249 | 0.693 | ||
| 体积 | 0.019 | 1.000 | -0.164 | 0.016 | -0.059 | ||
| 直径 | 圆度 | 0.234 | -0.164 | 1.000 | 0.134 | 0.239 | |
| 体态比 | 0.249 | 0.016 | 0.134 | 1.000 | 0.287 | ||
| 坑壁坡度 | 0.693 | -0.059 | 0.239 | 0.287 | 1.000 | ||
| 深径比 | 1.000 | -0.485 | 0.278 | 0.305 | 0.659 | ||
| 直径 | -0.485 | 1.000 | -0.145 | -0.189 | -0.115 | ||
| 体积 | 圆度 | 0.278 | -0.145 | 1.000 | 0.162 | 0.245 | |
| 体态比 | 0.305 | -0.189 | 0.162 | 1.000 | 0.303 | ||
| 坑壁坡度 | 0.659 | -0.115 | 0.245 | 0.303 | 1.000 | ||
| 深径比 | 1.000 | -0.494 | -0.188 | 0.278 | 0.635 | ||
| 直径 | -0.494 | 1.000 | 0.474 | -0.172 | -0.105 | ||
| 圆度 | 体积 | -0.188 | 0.474 | 1.000 | -0.048 | -0.068 | |
| 体态比 | 0.278 | -0.172 | -0.048 | 1.000 | 0.277 | ||
| 坑壁坡度 | 0.635 | -0.105 | -0.068 | 0.277 | 1.000 | ||
| 深径比 | 1.000 | -0.505 | -0.243 | 0.290 | 0.629 | ||
| 直径 | -0.505 | 1.000 | 0.504 | -0.227 | -0.109 | ||
| 体态比 | 体积 | -0.243 | 0.504 | 1.000 | -0.255 | -0.112 | |
| 圆度 | 0.290 | -0.227 | -0.255 | 1.000 | 0.229 | ||
| 坑壁坡度 | 0.629 | -0.109 | -0.112 | 0.229 | 1.000 | ||
| 深径比 | 1.000 | -0.576 | -0.228 | 0.206 | 0.155 | ||
| 直径 | -0.576 | 1.000 | 0.499 | -0.222 | -0.168 | ||
| 坑壁坡度 | 体积 | -0.228 | 0.499 | 1.000 | -0.241 | -0.055 | |
| 圆度 | 0.206 | -0.222 | -0.241 | 1.000 | 0.105 | ||
| 体态比 | 0.15 | -0.168 | -0.055 | 0.105 | 1.000 | ||
如表 7,在一级偏相关结果中,作为控制变量的直径、体积、圆度、体态比以及坑壁坡度,分别将深径比因子与其他除自身以外的指标间关联关系得到进一步简化,主要关系为:直径、体积、圆度、体态比这4个因子不同程度地对深径比与坑壁坡度两个因子之间的关联关系产生相对较大的影响。
同时,通过表 7偏相关分析结果可以得出,深径比对于表征撞击坑的退化是较好的评判指标[16],而深径比与坑壁坡度间的关联性同时受直径、体积、圆度和体态比的综合影响,并且偏相关性较好,这说明深径比因子与其他5个指标有着密切的联系,并且可能存在综合的量化关系。
2.4 复相关分析从计量地理学相关性分析的意义看,指标因子间的单相关分析和偏相关分析都是探讨两两因子之间的关联性。事实上,一个要素的变化往往受多种要素的综合作用和影响。从表 4分析结果可以得知,深径比指标和深度指标都可看作是量化撞击坑退化研究的因变量。因此,本文基于1 407个撞击坑样本数据,探讨最终因变量的选择以及因变量与其他因子之间的复相关关系,以量化各指标因子对于因变量的综合影响。复相关回归统计结果如表 8。
| F | 复相关系数R | R2 | 标准误差 | 观测值 | |
| 深度 | 435.513 | 0.780 | 0.609 | 890.857 | 1 407 |
| 深径比 | 492.037 | 0.798 | 0.637 | 0.039 2 | 1 407 |
由表 8可知,深径比与其他5个因子之间的相关性更好,且高度显著,因此选择深径比作为探索各指标关联性的因变量。而深径比与直径、体积、圆度、体态比和坑壁坡度之间的相关性也进一步证明,各指标作为撞击坑形态特征的指示因子,存在密切的数学联系,可进行多变量的综合回归模型分析。
2.5 基于多因子的量化关系模型构建虽然指标间的关联性分析已经说明深径比与直径、体积、圆度、体态比和坑壁坡度5个指标因子存在综合的数学关系,但从地理建模角度来看,各自变量应当对于因变量具有很好的可解释性和数学依赖性,并且自变量之间应当保持一定的独立性。
深径比与直径、坑壁坡度之间的相关性较好,而圆度、体态比与其他指标因子之间的相关性中,与深径比的关联性最好。并且除深径比之外的其他因子从不同视角对撞击坑形态都具有较好的地学表征意义。从单相关分析结果看,在作为5个自变量因子之间的相关性比较一般,因子之间的独立性较好。
综上所述,本文将以深径比为因变量(y),以直径(x1)、体积(x2)、圆度(x3)、体态比(x4)以及坑壁坡度(x5)为自变量,构建多元线性回归的量化关系模型。采用逐步回归模拟发现,各变量之间存在很强的线性函数关系:
| $ \begin{array}{l} y = (7.941{\rm{e}} - 007){x_1} + (8.063{\rm{e}} - 016){x_2} + 0.082{x_3} + 0.012{x_4} + 0.007{x_5} - 0.042. \end{array} $ | (1) |
本文从模型的拟合优度、方程的显著性、变量显著性与参数的置信区间4方面对模型进行统计检验。拟合模型的复相关系数为0.798,回归模型的概率为0.00,明显小于显著性水平0.05。模型的拟合优度达0.637,调整后的拟合优度达0.639。回归模型的方差分析结果见表 9。经过显著性检验,在0.05的置信水平下查F分布表可知:Fa(k, n-k-1)=F0.05(5, 1401)=2.21,在回归拟合结果中,F=492.037>>Fa。因此,在0.05的置信水平下,回归模拟函数是极显著的。
| 平方和 | df | 均方 | F | Sig. F | |
| 回归 | 3.787 | 5 | 0.757 | 492.037 | 0.00b |
| 残差 | 2.156 | 1 401 | 0.002 | ||
| 总计 | 5.943 | 1 407 |
本文从撞击坑的尺寸特征、发育特征等角度总结了前人对撞击坑形态特征的基本认识和量化研究成果;利用100 m分辨率的数字高程模型数据,通过对撞击坑各形态因子分析筛选给出了撞击坑形态的多元线性回归拟合模型,这种拟合关系反映了撞击坑形态特征的指标因子传递出的撞击坑发育的数学机理,揭示了撞击坑形态发育指标因子之间的内在联系,而不再是单一的因子量化特征表达。通过对描述月表撞击坑形态参数指标的关联性分析和量化模拟研究,可得出以下结论:
(1) 在文[13]对撞击坑分类的基础上,将撞击坑划分为6种类型,对选取的1 407个撞击坑进行量算,新鲜撞击坑的深径比平均值为0.187,退化撞击坑的深径比平均值为0.077 1,其他撞击坑形态参数指标的差异如表 2。
(2) 对8个撞击坑形态指标进行偏相关和复相关分析,确定以深径比为因变量,直径、体积、圆度、体态比和坑壁坡度为自变量构建指标因子的量化模拟,得到其线性拟合公式,模型的拟合优度达0.637,调整后的拟合优度达0.639,说明本文的拟合模型能够较好地表达撞击坑形态发育特征。
(3) 模型的复相关系数为0.798,在0.05置信水平的显著性F=492.037>>Fa,说明构建的模型显著性较好,可用于月表撞击坑形态发育特征的预测和估计。
此外,本文还对所选择的指标因子进行非线性拟合,深径比与直径、坑壁坡度的拟合优度分别为0.471 5、0.452 4,而深径比与体积、圆度、体态比的拟合优度都小于0.15,也说明深径比与其他指标因子之间不适宜多元非线性拟合。
本文基于撞击坑形态特征,实现多因子量化关系建模表达撞击坑形貌发育的演化机理,揭示描述撞击坑形貌的地形因子信息与月球空间环境系统之间规律的过程,对于多因子联合定量表达的撞击坑形貌信息建模研究和撞击坑形貌形态发育研究有重要的实践意义。
然而,在利用建模的理论和方法实现撞击坑形态数字地形信息挖掘方面,还需开展大量的工作。在指标选取上要进行更多的尝试,以增强模型构建的稳定性。提取全月撞击坑形态指标数据,对模型进行全月撞击坑数据的验证,探讨以模型为依据, 结合月表岩性分类研究[17]的撞击坑类型分类是未来的工作重点。
| [1] | MIYAMOTO S. Morphological study of the lunar crust[J]. Icarus, 1968, 9(1): 373–390. |
| [2] | 欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005: 2-3. |
| [3] | HUANG Q, PING J S, SU X L, et al. New features of the Moon revealed and identified by CLTM-s01[J]. Science in China:Physics, Mechanics & Astronomy, 2009, 52(12): 1815–1823. |
| [4] | 刘宇轩, 刘建军, 牟伶俐, 等. 撞击坑识别方法综述[J]. 天文研究与技术——国家天文台台刊, 2012, 9(2): 203–212 |
| [5] | 赵金锦, 刘建军, 牟伶俐. 月表撞击坑形貌特征和几何形态关系分析[J]. 天文研究与技术——国家天文台台刊, 2014, 11(1): 80–88 |
| [6] | The Cognizance of the Marshall Space Flight Center. Lunar surface model[R]. Washington: National Aeronautics and Space Adminitration, 1969. |
| [7] | 郑丽. 行星撞击坑分形及分维数意义探讨[J]. 河北师范大学学报(自然科学版), 1998, 22(3): 347–351 |
| [8] | 严艳梓, 汤国安, 熊礼阳, 等. 基于DEM的月球雨海地区粗糙度研究[J]. 地理研究, 2014, 33(8): 1442–1456 |
| [9] | 王娇, 程维明, 周成虎, 等. 全月球撞击坑形貌特征的识别与多指标表达[J]. 地理研究, 2014, 33(7): 1251–1263 |
| [10] | 王心源, 吉玮, 李超, 等. 基于"嫦娥一号"数据的月表撞击坑特征的多参数统计分析[J]. 地理研究, 2012, 31(2): 369–376 |
| [11] | CHEN M, LEI M L, LIU D Y, et al. Morphological features-based descriptive index system for lunar impact craters[J]. ISPRS International Journal of Geo-Information, 2017, 7(1): article id. 5(22pp). |
| [12] | IVANOV B A. Size-frequency distribution of small lunar craters:widening with degradation and crater lifetime[J]. Solar System Research, 2018, 52(1): 1–25. DOI: 10.1134/S0038094618010021 |
| [13] | MAHANTI P, ROBINSON M S, THOMPSON T J, et al. Small lunar craters at the Apollo 16 and 17 landing sites-morphology and degradation[J]. Icarus, 2018, 299: 475–501. DOI: 10.1016/j.icarus.2017.08.018 |
| [14] | CHEN M, LIU D Y, QIAN K J, et al. Lunar crater detection based on terrain analysis and mathematical morphology methods using digital elevation models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(7): 3681–3692. DOI: 10.1109/TGRS.2018.2806371 |
| [15] | ZHOU Y, ZHAO H, CHEN M, et al. Automatic detection of lunar craters based on DEM data with the terrain analysis method[J]. Planetary and Space Science, 2018, 160: 1–11. DOI: 10.1016/j.pss.2018.03.003 |
| [16] | PIKE R J. Depth/diameter relations of fresh lunar craters-revision from spacecraft data[J]. Geophysical Research Letters, 1974, 1(7): 291–294. DOI: 10.1029/GL001i007p00291 |
| [17] | 蔡婷妮, 李春来, 任鑫, 等. 基于遥感探测数据的月球玄武岩分类研究进展[J]. 天文研究与技术, 2017, 14(2): 179–191 |



