2. 中国科学院空间天文与技术重点实验室, 北京 100101;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Space Astronomy and Technology, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
光学综合孔径技术是将多个小口径的光学元件或系统以某种构型进行精确排列,使通过各子孔径的光束在焦平面上实现光场的相干叠加,经图像复原技术处理后,达到与单一大口径系统相当的衍射极限分辨率的技术,它可以突破单口径望远镜衍射极限的限制。
光学综合孔径望远镜按照拼接方式的不同,分为拼接主镜和拼接子镜两种形式。目前,世界各国已建立了多台拼接子望远镜形式的光学综合孔径望远镜。2002年,美国麻省理工学院建立了白光自适应GOLAY-3型ARGOS(Adaptive Reconnaissance Golay-3 Optical Satellite)望远镜[1],它由3个孔径为21 cm的子望远镜组成,角分辨率0.35″,光谱范围400~700 nm,视场为3′ × 3′,等效口径0.62 m,信噪比100。美国洛克希德·马丁公司联合美国国家航空航天局、喷气推进实验室、加州理工学院、加利福尼亚大学和罗切斯特大学,建立了空间多仪器口径分布式传感系统(Multiple Instrument Distributed Aperture Sensor, MIDAS)[2],该系统能够实现大视场、衍射极限成像,可以在5 000 km的轨道上进行对地观测,地面分辨率小于1 m,也可以在100 km的轨道上进行高分辨率成像, 地面分辨率达到2 cm。
光学综合孔径望远镜在进行干涉成像时,必须实现光束的相干叠加,才能提高图像的空间分辨率。对于白光宽带成像系统,由于光源的相干长度非常小,相当于要求不同路径的光束实现零等光程干涉。因此,对光程差进行精确探测,成为实现光干涉的先决条件。
目前,国内外在光程探测领域已开展了大量的研究。出瞳面检测:四棱锥波前检测法通过探测出瞳处4个像点的能量差异计算光程差[3]。离焦面检测:相位恢复法通过焦面和离焦面的一对光强分布数据反解各自的相位分布[4]。焦面检测法:(1)窄带-哈特曼夏克法和宽带-哈特曼夏克法通过检测采样孔径衍射图样和“样板图样”的相关系数,计算拼接子镜间的光程差[5]。(2)色散条纹法通过检测所提取的相邻孔径之间的干涉条纹中横向光强信号,对其进行非线性最小二乘拟合求解光程差[6]。
为了尽可能达到光程差探测范围大于±50 μm、探测精度小于20 nm的技术指标,利用国家天文台空间天文技术实验室建立的光学综合孔径原理样机系统,对基于傅里叶变换的色散条纹法进行理论推导和算法设计,并开展了开环和闭环实验。在开环实验中,采集不同光程差的色散条纹图像,通过图像频谱次峰偏移量解算光程差,并与设定的光程差进行比对,验证方法的线性关系;在闭环实验中,对人为引入的光程差进行实时计算和闭环控制,观察系统对光程差变化的校正能力。
1 理论基础基于色散条纹法的焦平面光强分布表达式为[7]
| $ I(x, y) = {I_0}\left\{ {1 + \gamma \cos \left[ {\frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda (x)}}\phi + {\varphi _0}(y)} \right]} \right\}, $ | (1) |
其中,I0为平均光强;γ为条纹对比度;ϕ为光程差;λ(x)=λ0+C0x,其中λ0为中心波长,x为色散方向,C0为线色散率;φ0(y)为初相位。由于波数的表达式
| $ I(x, y) = {I_0}\left\{ {1 + \gamma \cos \left[ {\left( {{k_0} - \frac{{{k_0}^2{C_0}}}{{2{\rm{ \mathsf{ π} }}}}x} \right)\phi + {\varphi _0}(y)} \right]} \right\}, $ | (2) |
对(2)式进行二维傅里叶变换,得到:
| $ {{I}_{\text{F}}}\left( {{f}_{x}}, {{f}_{y}} \right)=\iint{I}(x, y){{\text{e}}^{\left[ -2\text{ }\!\!\pi\!\!\text{ }\left( x{{f}_{x}}+y{{f}_{y}} \right)\text{j} \right]}}\text{d}x\text{d}y. $ | (3) |
由于(2)式中的余弦项可以用欧拉公式表达,因此I(x, y)中余弦项可表示为
| $ \cos \left[ \left( {{k}_{0}}-\frac{{{k}_{0}}^{2}{{C}_{0}}}{{2{\rm{\pi }}}}x \right)\phi +{{\varphi }_{0}}(y) \right]=\frac{{{\text{e}}^{\left[ \left( {{k}_{0}}-\frac{{{k}_{0}}^{2}{{C}_{0}}}{{2{\rm{\pi }}}}x \right)\phi +{{\varphi }_{0}}(y) \right]\text{j}}}}{2}+\frac{{{\text{e}}^{-\left[ \left( {{k}_{0}}-\frac{{{k}_{0}}^{2}{{C}_{0}}}{{2{\rm{\pi }}}}x \right)\phi +{{\varphi }_{0}}(y) \right]\text{j}}}}{2}, $ | (4) |
用(4)式表示(2)式中的余弦项,得到I(x, y)的二维频谱表达式:
| $ \begin{align} & {{I}_{\text{F}}}\left( {{f}_{x}}, {{f}_{y}} \right)={2{\rm{\pi }}}{{I}_{0}}\delta \left( {{f}_{x}}, {{f}_{y}} \right)+\text{ }\!\!\pi\!\!\text{ }{{I}_{0}}\gamma {{\text{e}}^{-{{k}_{0}}\phi \text{j}}}\delta \left( {{f}_{x}}+\frac{{{C}_{0}}{{k}_{0}}^{2}}{{2{\rm{\pi }}}}\phi , {{f}_{y}}-A \right) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\text{ }\!\!\pi\!\!\text{ }{{I}_{0}}\gamma {{\text{e}}^{{{k}_{0}}\phi \text{j}}}\delta \left( {{f}_{x}}-\frac{{{C}_{0}}{{k}_{0}}^{2}}{{2{\rm{\pi }}}}\phi , {{f}_{y}}+A \right) \\ \end{align}, $ | (5) |
其中,假设A为两个次峰相对于x轴的偏移量。在I(x, y)的频谱中有3个峰,其中主峰位于(0, 0),两个次峰分别位于
| $ dx = \frac{{{C_0}{k_0}^2}}{{2{\rm{ \mathsf{ π} }}}}\phi , $ | (6) |
其中,C0和k0均为常数。因此,频谱次峰相对于y轴的偏移量dx与光程差ϕ之间呈现良好的线性关系,故可以用基于傅里叶变换的方法对色散条纹图像进行处理,从而求得光程差。
2 光程探测算法流程设计基于色散条纹图像的光程探测算法流程如图 1[8]。首先,读取某一光程差的干涉条纹图像,然后对其进行二维傅里叶变换,并求取幅值。得到频谱图像后,首先将主峰所在的区域全部置0,然后求取最大幅值所在的位置,此时求得的就是两个次峰所在的位置。选取其中一个次峰,并确定该次峰相对于y轴的偏移量dx,以该次峰所在位置为中心,进行亚像素精度拟合,设次峰位于(x, y),幅值为F(x, y),拟合式为[9]
| $ dx' = dx + \frac{{0.5[F(x - 1, y) - F(x + 1, y)]}}{{F(x - 1, y) + F(x + 1, y) - 2F(x, y)}}. $ | (7) |
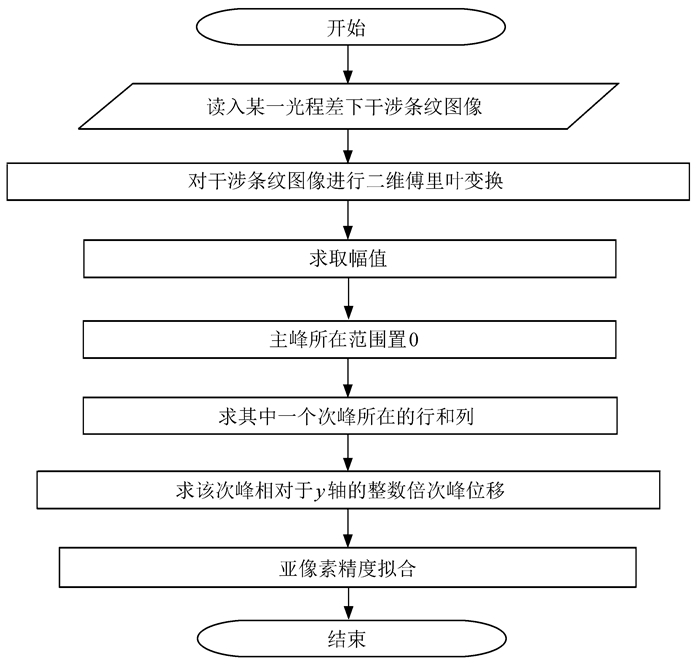
|
| 图 1 基于一幅图像的光程探测算法流程图 Fig. 1 Piston error detection algorithm flow based on one image |
在此基础上,乘以一个比例系数就可以求得光程差值,比例系数可以通过计算得到,也可由实验进行标定,至此,对于一幅干涉条纹图像的光程差求解过程结束。
3 光学综合孔径实验系统国家天文台建立的Fizeau型光学综合孔径实验装置由光源系统、子望远镜系统、指向探测和补偿系统、光程探测和补偿系统、合光成像及处理系统5部分组成,如图 2[10]。其电子学系统由图像分发板、3块计算控制板、数模输出板、模拟电源板、数字电源板和接口底板共8块板卡组成,如图 3。在开环实验中,采集色散条纹的系列图像,利用MATLAB求解光程差。在闭环实验中,利用电子学系统,基于Visual Dsp++5.0开发TS201程序,进行光程差的实时探测及控制。

|
| 图 2 原理样机系统 Fig. 2 Principle prototype system |

|
| 图 3 电子学系统 Fig. 3 Electronic system |
在实验中,光源系统均采用NKT Photonics公司的SuperK EXTREME系列高功率超连续白光光源,其滤光器输出光谱范围为400~700 nm,具有波段中心、波段宽度、输出功率可调的特点。光源望远镜是典型的卡塞格林望远镜,具有500 mm通光孔径,20 m焦距,大于2 arcmin的视场角,F/#40。子望远镜系统由3路子望远镜组成,采用反射式无焦系统,放大率为5,基线长度200 mm,入射光束口径100 mm,出射光束口径20 mm,系统组合焦距4 500 mm。为保证经子望远镜1#,2#,3#的3路光束可进行相干成像,光程探测模块内设置两个光程探测望远镜,以子望远镜1#为基准,分别对1#,2#和1#,3#进行光程探测并解算出光程差值,最终达到控制3路光束间光程差的目的。其中1#,2#和1#,3#间的两路光束经光程探测模块内的Amici色散棱栅以及光程探测望远镜后,在焦面上形成色散干涉条纹。光程补偿模块分为粗调平台和精调平台,如图 4。在开环实验中,利用光程补偿组件中的粗调平台(PI公司的M-122微位移平台)调整运动反射镜的位置,改变光学延迟线的大小,从而得到不同光程差下的干涉条纹图像。M-122微位移平台以线性编码器作为集成传感器,行程25 mm,分辨率0.1 μm,最小位移0.2 μm,最大速度20 mm/s。在闭环实验中,利用光程补偿组件中的精调平台(PI公司的P-753促动器)对光程差进行精补偿。P-753促动器带有电容式集成传感器,行程12 μm,分辨率0.05 nm,重复精度±1 nm。合光成像系统是由1个合光成像望远镜组成,该望远镜为卡塞格林式,口径110 mm,焦距1 680 mm。在完成倾斜误差与光程差的校正后,该系统将3路光束进行相干成像。

|
| 图 4 光程补偿组件中的粗调平台和精调平台 Fig. 4 Piston compensation elements coarse and fine adjustment platform |
在开环实验中,设置NKT光源输出的光谱范围为550~650 nm、中心波长为600 nm。通过移动M-122平台,在-90 μm至+90 μm的光程差范围内,以1 μm为间隔,采集两束光干涉所形成的181幅色散干涉条纹图像。图 5、图 6中,从上至下分别为-60 μm,0 μm,+60 μm光程差下的色散干涉条纹图像及其频谱。当光程差为0时,干涉条纹未发生倾斜。当光程差为正、负时,干涉条纹分别斜向下、斜向上倾斜。由于干涉条纹的倾斜线与两个次峰之间的连接线互相垂直[8],因此当光程差为0时,两个次峰对称分布于y轴正、负半轴。当光程差为正、负时,两个次峰对称分布于一、三象限和二、四象限。

|
| 图 5 不同光程差的干涉条纹图像 Fig. 5 Interference fringe images with different piston errors |

|
| 图 6 与干涉条纹图像对应的频谱图 Fig. 6 Spectrograms related to interference fringe images |
对181幅图像求得的偏移量dx′及其拟合结果如图 7。其中横坐标为光程差设定值,单位μm,纵坐标为所选取的位于x轴上方的次峰相对于y轴的偏移量dx′,单位为pixel。红色圆点为181个光程差对应的偏移量dx′,蓝色直线为181个偏移量的线性拟合结果,拟合式为dx′=0.253 6ϕ + 0.910 4,因此可以通过该表达式计算181个光程差值。图 8为实际求解光程差与设定光程差的对比图,其中横坐标为设定光程差,单位μm,纵坐标为实际解算的光程差值,单位为μm。绿色圆点为实际求解181个光程差的分布,蓝色直线为设定的光程差值。所求解的部分偏移量dx′及实际光程差ϕ如表 1、表 2。
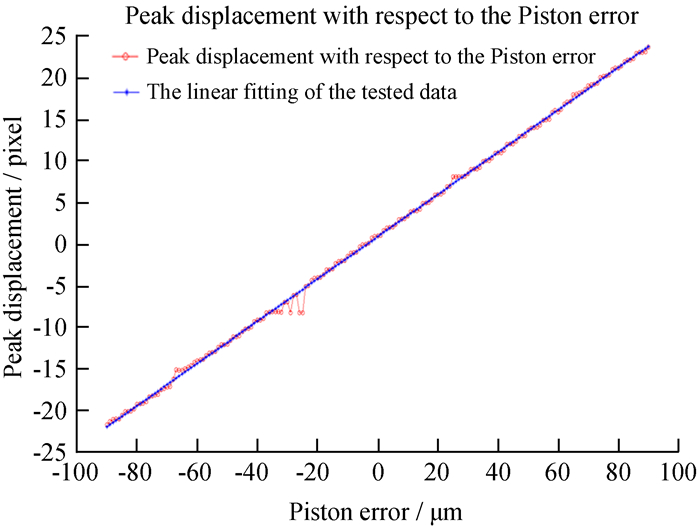
|
| 图 7 偏移量求解及线性拟合结果 Fig. 7 Peak displacements and linear fitting results |
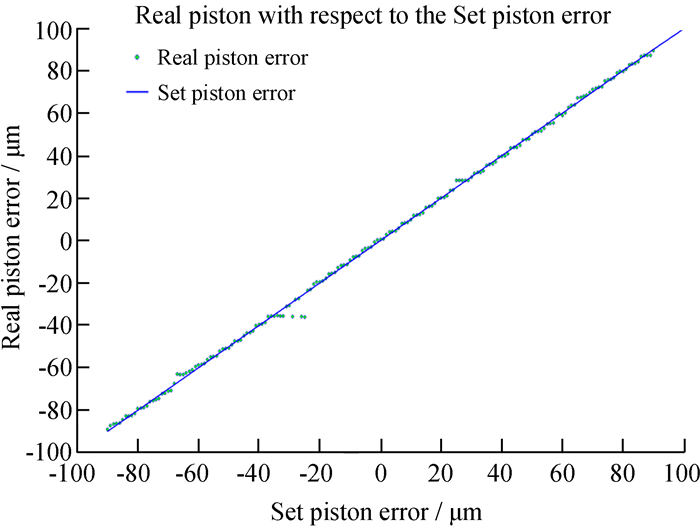
|
| 图 8 设定光程差与实际光程差对比图 Fig. 8 Set and real piston errors comparison |
| 设定值/μm | -60 | -40 | -20 | 0 | 20 | 40 | 60 |
| 偏移量/pixel | -14.0 | -9.1 | -4.0 | 1.0 | 6.0 | 11.0 | 15.9 |
| 设定值/μm | -60 | -40 | -20 | 0 | 20 | 40 | 60 |
| 解算值/μm | -58.7 | -39.5 | -19.5 | 0.4 | 20.0 | 39.7 | 59.0 |
在得到-90 μm至+90 μm范围内的光程差计算结果后,计算了均方根误差值。设ϕi为设定光程差值,ϕd为实际解算的光程差值,测量误差ε的表达式为
| $ \varepsilon = {\phi _{\rm{d}}} - {\phi _{\rm{i}}}. $ | (8) |
在开环实验中,计算得到181个光程差的均方根误差εrms为1.564 μm。
5 闭环实验光学综合孔径系统光程探测及闭环控制框图如图 9,其中,δset为设定的光程差;δact为实测的光程差。利用基于傅里叶变换的光程计算方法,通过数字信号处理器完成光程差的实时计算,驱动执行机构,即P-753。通过改变镜面的位置,从而对光程差进行补偿控制。控制方法采用离散比例-积分-微分控制(PID),其中比例控制的动作与偏差大小成正比,作用是以某一比例对稳态误差进行消除,积分控制的动作与偏差对时间的积分成正比,作用是消除每次采样时刻产生的余差,微分控制的动作与偏差的变化速度成正比,作用是阻止被调参数的变化,有超前调节的作用。增量式比例-积分-微分控制(PID)表达式为
| $ \begin{array}{l} u(k) = u(k - 1) + {K_{\rm{p}}}[e(k) - e(k - 1)] + {K_{\rm{i}}}e(k) + {K_{\rm{d}}}[e(k) - 2e(k - 1) + e(k - 2)]\\ \;\;\;\;\;\;\; = u(k - 1) + {q_0}e(k) + {q_1}e(k - 1) + {q_2}e(k - 2) \end{array} $ | (9) |

|
| 图 9 光学综合孔径光程探测及闭环控制框图 Fig. 9 Optical synthetic aperture piston error detection and close-loop control diagram |
其中,q0=Kp+Ki+Kd;q1=-Kp-2Kd;q2=Kd,u(k)为第k次采样的输出,Kp,Ki,Kd分别代表PID控制器的比例系数、积分系数和微分系数。
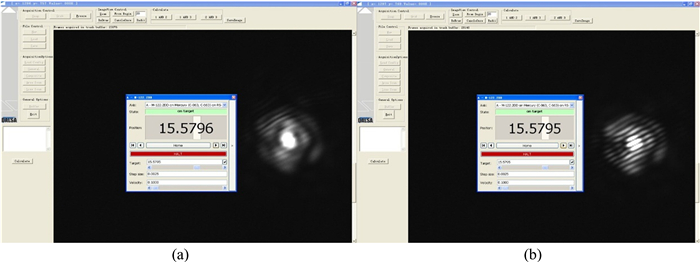
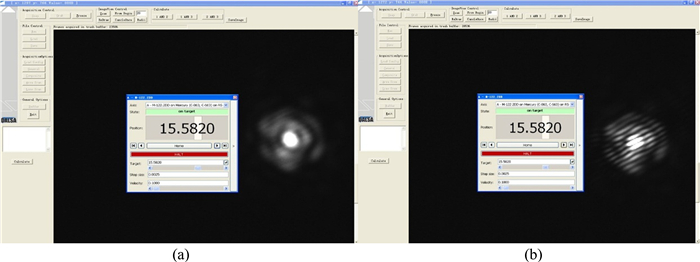
在闭环实验中,同样使用NKT光源,中心波长为600 nm,光谱范围为550~650 nm。设置Kp=0,Ki=0.04,Kd=0。图 10、图 11、图 12分别为调节到零光程、2.5 μm光程差以及5 μm光程差时的开、闭环实验结果。当系统处于开环状态时,干涉条纹图像随着光程差的增加发生偏移。当系统处于闭环状态时,不管光程差如何变化,干涉条纹始终稳定在零光程的位置,表明光程差的闭环控制取得了良好的效果。
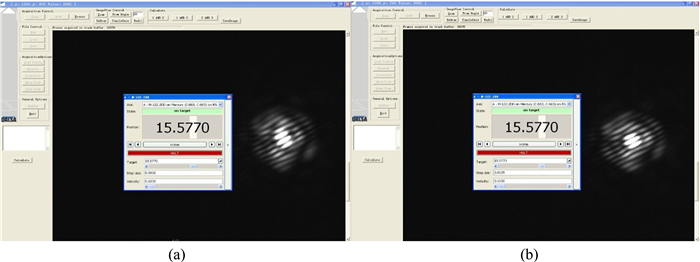
|
| 图 10 (a) 零光程开环实验;(b)闭环实验 Fig. 10 (a) 0μm piston error open-loop experiments; (b) close-loop experiments |
|
| 图 11 (a) 2.5 μm光程差开环实验;(b)闭环实验 Fig. 11 (a) 2.5μm piston error open-loop experiments; (b) close-loop experiments |
|
| 图 12 (a) 5 μm光程差开环实验;(b)闭环实验 Fig. 12 (a) 5μm piston error open-loop experiments; (b) close-loop experiments |
本文主要介绍了开展基于傅里叶变换的色散条纹法进行光程探测及开环、闭环实验的结果。首先,进行理论推导,得到次峰相对于y轴偏移量与光程差之间的线性关系。然后,进行算法流程设计。最后,利用实验室的光学综合孔径实验装置,进行了开环、闭环实验。在开环实验中,采集多幅不同光程差的色散条纹图像,对图像频谱次峰偏移量和光程差的关系展开研究,结果显示,偏移量与光程差之间呈现良好的线性关系;在闭环实验中,利用光程差的实时计算结果和光程补偿机构对光程差进行闭环控制,结果显示,在外加扰动的情况下,系统能够始终保持在初始的干涉状态。
| [1] | 白静, 姜爱民, 戴妍峰. Golay3型光学稀疏孔径系统退化图像的频率信息提取及合成研究[J]. 天文研究与技术, 2016, 13(3): 351–357 DOI: 10.3969/j.issn.1672-7673.2016.03.012 |
| [2] | NI M, BENSON L, CAMP J, et al. Autonomous tip/tilt alignment and phasing of a distributed aperture imaging testbed[J]. Optics Express, 2010, 18(12): 13051–13056. DOI: 10.1364/OE.18.013051 |
| [3] | ESPOSITO S, DEVANEY N. Segmented telescopes co-phasing using Pyramid Sensor[C]//Proceedings of the European Southern Observatory Conference and Workshop. 2002. |
| [4] | BOLCAR M R. Phase diversity for segmented and multi-aperture systems[D]. Rochester: University of Rochester, 2008. http://www.researchgate.net/publication/36712548_Phase_diversity_for_segmented_and_multi-aperture_systems |
| [5] | CHANAN G, OHARA C, TROY M. Phasing the mirror segments of the Keck telescopes Ⅱ:the narrow-band phasing algorithm[J]. Applied Optics, 2000, 39(25): 4706–4714. DOI: 10.1364/AO.39.004706 |
| [6] | 张勇, 张靓. 色散条纹传感技术用于拼接镜面位移探测的仿真研究[J]. 中国科学院研究生院学报, 2010, 27(4): 471–479 |
| [7] | 刘清, 姜爱民. 光学综合孔径望远镜光程探测方法研究[J]. 天文研究与技术, 2017, 14(4): 519–525 |
| [8] | VAN DAM M A, MCLEOD B A, BOUCHEZ A H. Dispersed fringe sensor for the Giant Magellan Telescope[J]. Applied Optics, 2016, 55(3): 539–547. DOI: 10.1364/AO.55.000539 |
| [9] | POYNEER L A. Scene-based Shack-Hartmann wave-front sensing:analysis and simulation[J]. Applied Optics, 2003, 42(29): 5807–5815. DOI: 10.1364/AO.42.005807 |
| [10] | JIANG A M, WANG S, DONG Z C, et al. Wide-band white light sparse-aperture Fizeau imaging interferometer testbed for a distributed small-satellites constellation[J]. Applied Optics, 2018, 57(11): 2736–2746. DOI: 10.1364/AO.57.002736 |


