2. 中国科学院国家天文台, 北京 100101;
3. 中国科学院月球与深空探测重点实验室, 北京 100101
2. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China;
3. Key Laboratory for Exploration in the Moon and Deep Space, Chinese Academy of Sciences, Beijing 100101, China
随着人类探索太空能力的不断增强,深空探测领域已成为航天领域的热点[1],其中,以月球为目标的探测任务达到了将近一半的比例。月表测绘制图是月球探测的重要任务之一,主要通过月球探测器携带的科学载荷获取探测数据,然后利用摄影测量技术进行处理和计算,得到月表正射影像、月表三维地形图等。我国近期发射的月球探测器,包括嫦娥三号、嫦娥四号和嫦娥五号都携带了两台全景相机,负责探测器着陆区影像数据采集的任务。全景相机获取的影像数据用于制作月表着陆区厘米级精度的地形数据,该成果能够为深入研究探测点附近准确的地质构造提供精确的形貌数据,为其它载荷(如矿物光谱仪)数据的综合研究提供基础数据,同时也是月球车探测点规划的重要参考数据之一,因此,对于后续的研究意义重大。两台全景相机固定于巡视器的转台上,工作时采用双目立体成像,相机间的相对位置和姿态关系(以下简称相对外方位元素)保持不变,是后续摄影测量平差处理的重要约束条件之一。
目前主流的商业摄影测量软件,包括smart 3D,photoscan等在稀疏匹配时都是以单幅影像为单位进行光束法平差计算,成像模型基于摄影测量学的共线方程[2]:
| $ {x - {x_0} = - f\frac{{\left( {X - {X_0}} \right){R_{11}} + \left( {Y - {Y_0}} \right){R_{21}} + \left( {Z - {Z_0}} \right){R_{31}}}}{{\left( {X - {X_0}} \right){R_{13}} + \left( {Y - {Y_0}} \right){R_{23}} + \left( {Z - {Z_0}} \right){R_{33}}}}} $ | (1) |
| $ {y - {y_0} = - f\frac{{\left( {X - {X_0}} \right){R_{12}} + \left( {Y - {Y_0}} \right){R_{22}} + \left( {Z - {Z_0}} \right){R_{32}}}}{{\left( {X - {X_0}} \right){R_{13}} + \left( {Y - {Y_0}} \right){R_{23}} + \left( {Z - {Z_0}} \right){R_{33}}}}} $ | (2) |
其中,x0,y0,f为相机的内方位元素;X0,Y0,Z0为相机的投影中心;R为旋转矩阵。
该方法未加入相机间的相对约束关系,每幅影像都是自由地旋转平移以达到光线束的最佳交会,因此解算得到的左右相机的相对外方位元素不是严格固定的,由左右相机构成的立体像对解算的三维坐标必然存在一定的误差。
目前已经有大量关于行星表面全景相机双目立体影像的处理案例,文[3]总结了美国“勇气号”和“机遇号”的定位与制图方法,提出平差方法主要来源于光束法平差及其改进算法,文[4]利用嫦娥三号全景相机的双目立体影像实现了月表地形的三维重建,算法部分主要利用基于摄影测量学共线方程的前方交会算法。经过大量的文献调研和总结发现,目前行星表面双目立体成像数据处理大多采用基于传统共线方程的平差算法,很少考虑左右相机相对外方位元素固定的约束条件。
在航空摄影领域,多视影像成像同样存在相机间相对外方位元素固定的情况,与本文研究的月表全景相机成像方式有相似之处,且已经有大量的研究成果。文[5]针对多镜头的MOMS-02相机提出了一种改进的成像模型。文[6]提出了倾斜航空摄影中,考虑同一测站下视与斜视相机间的约束关系,采用6个偏心参数描述两者之间的变换。文[7]提出多视影像的倾斜航空影像区域网可以采用3种平差方式,包括无约束的联合定向方式、附加相对约束的定向方式以及直接定向方式。
本文在调研了大量航空摄影多视影像平差方法的文献后,总结出一种附加相对约束关系的月表全景相机平差算法,主要是将同一测站左右相机的相对外方位元素保持不变的条件加入光束法平差模型中,将每个摄站的多个相机整体作为一个刚体单位进行平差计算,该方法的平差模型更加严密,网型更加稳定。经过验证,该平差模型能够保证同一测站两台全景相机的相对外方位元素保持不变,并且减少了平差模型中的未知数,能够为我国探月任务中月表全景相机的摄影测量处理提供技术支持。
1 月表全景相机及实验数据简介本次实验数据包括嫦娥三号巡视器全景相机环拍数据和嫦娥五号全景相机外场科学验证试验数据,全景相机参数见表 1。两组数据的成像方式均为全景相机双目立体成像,影像数据获取过程中保持左右相机相对外方位元素不变。
| 波段范围 | 颜色 | 成像模式 | 正常成像 距离/m | 有效像元数量 | CCD探测器 像元大小/μm | |
| 嫦娥五号 全景相机 | 可见光 | 彩色 (R, G, B) | 彩色成像、全色成像 (可切换) | 3~∞ | 2 352 × 1 728 (彩色) 1 176 × 864 (全色) | 7.4 |
| 嫦娥三号 全景相机 | 可见光 | 彩色 (R, G, B) | 彩色成像、全色成像 (可切换) | 3~∞ | 2 352 × 1 728 (彩色) 1 176 × 864 (全色) | 7.4 |
嫦娥五号全景相机科学验证试验的目的在于评价相机影像质量、验证全景相机几何参数和安装参数的测量方案。试验分为内场和外场两部分,其中外场试验于2015年11月29日开展,外场全景如图 1。全景相机在两种不同姿态条件下完成了两组图像数据的获取,图像数据覆盖了试验点附近180°水平范围和-90°~0°俯仰范围,总共获取了195对影像数据,数据总量约3 GB。本文选取其中一组试验数据,共包括93对影像。

|
| 图 1 嫦娥五号全景相机科学验证试验外场区域 Fig. 1 Outfield of scientific verification test for panoramic cameras in Chang′E-5 |
嫦娥三号巡视器搭载了全景相机的科学载荷,主要用于获取巡视区月表的三维光学影像,在着陆器与巡视器实现两器月面分离后,巡视器围绕着陆器一圈获取了月表影像。全景相机在第1个月昼期间,在两器月面互拍点A、D上以彩色模式对着陆器成像51对,在N0106点上分别以俯仰角-7°和-19°,偏航角175°~176°的探测模式对巡视器周围月面进行360°环拍,分别获取了112对全色图像和56对彩色图像。第2个月昼期间,全景相机以彩色成像模式在N0203和N0205两个探测点对月面进行环拍,共获取环拍数据112对。本文选取第1月昼在E点和S3点的全色图像环拍数据,包括56对影像。图 2为嫦娥三号在N0106点获取的部分影像数据。

|
| 图 2 嫦娥三号全景相机在N0106点获取的部分影像 Fig. 2 Partial images taken by panoramic cameras in Chang′E-3 in point N0106 |
为方便推导,首先说明摄影测量学中几个重要的坐标系。
(1) 像平面坐标系:摄影方向与影像平面的交点称为像主点,以像主点为原点,两对边机械框标的连线为x轴和y轴,其中与航线方向一致的连线为x轴,航线方向为正向。
(2) 像空间坐标系:用于表示像点在像方空间的过渡坐标系,以摄影中心为原点,主光轴为z轴,正向为摄影的反方向,x,y轴与像平面坐标系的x,y轴平行。
(3) 像空间辅助坐标系:以摄影中心为原点,以铅垂方向为Z轴,航线方向为X轴,可以通过外方位元素构成的旋转矩阵对像空间坐标系进行旋转变换得到。
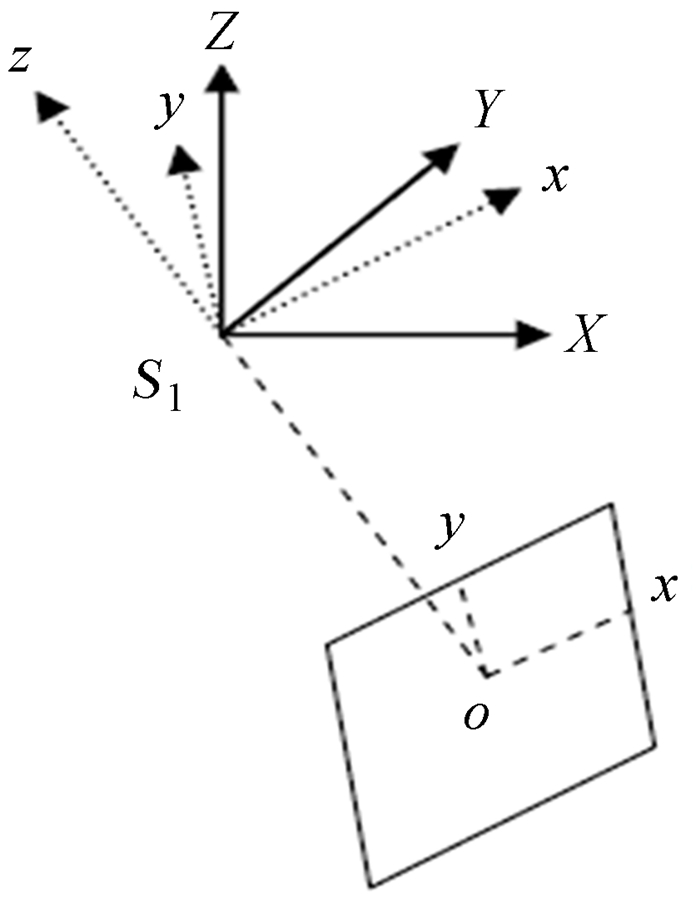
如图 3,o-xy为像平面坐标系,S1-xyz为像空间坐标系,S1-XYZ为像空间辅助坐标系。设左相机的投影中心为S1,S1的物方坐标为(X S1, Y S1, Z S1),外方位元素构成的旋转矩阵为R1,右相机的投影中心为S2,S2的物方坐标为(X S2, Y S2, Z S2),外方位元素构成的旋转矩阵为R2。设右相机的像空间坐标系旋转至与左相机的像空间坐标系平行时,旋转矩阵为M。
|
| 图 3 3个坐标系的位置关系 Fig. 3 Position relationships of three coordinate systems |
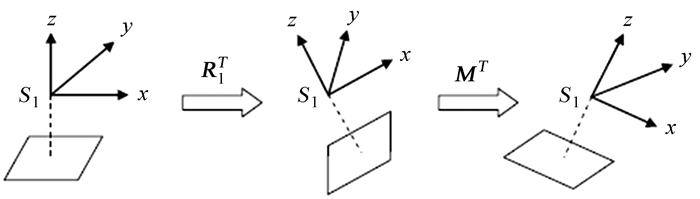
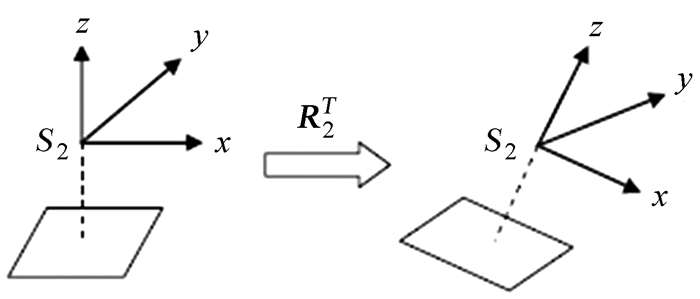
如图 4,对于左相机,由像空间辅助坐标系旋转至像空间坐标系,再旋转到右相机的像空间坐标系,旋转变换表示为MTR1T,如图 5,对于右相机,由像空间辅助坐标系旋转至像空间坐标系,旋转变换表示为R2T,两者的旋转是等价的,即
| $ {\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{R}}_1^{\rm{T}} = \mathit{\boldsymbol{R}}_2^{\rm{T}} $ | (3) |
|
| 图 4 左相机旋转过程 Fig. 4 Rotation process of left camera |
|
| 图 5 右相机旋转过程 Fig. 5 Rotation process of right camera |
设S1到S2的平移量为(Δx, Δy, Δz),该平移量以左相机的像空间坐标系为参照。于是,有以下关系:
| $ \left[ {\begin{array}{*{20}{c}} {{X_{{S_2}}}}\\ {{Y_{{S_2}}}}\\ {{Z_{{S_2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_{{S_1}}}}\\ {{Y_{{S_1}}}}\\ {{Z_{{S_1}}}} \end{array}} \right] + {\mathit{\boldsymbol{R}}_1}\left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y}\\ {\Delta z} \end{array}} \right]. $ | (4) |
原共线方程为
| $ \left[ {\begin{array}{*{20}{c}} {x - {x_0}}\\ {y - {y_0}}\\ { - f} \end{array}} \right] = k\mathit{\boldsymbol{R}}_2^{\rm{T}}\left[ {\begin{array}{*{20}{c}} {X - {X_{{S_2}}}}\\ {Y - {Y_{{S_2}}}}\\ {Z - {Z_{{S_2}}}} \end{array}} \right], $ | (5) |
其中,x0,y0,f为右相机的内方位元素;X,Y,Z和x,y为观测点的物方坐标和像平面坐标;k为比例系数。
将(3)式、(4)式代入(5)式,得到:
| $ \left[ {\begin{array}{*{20}{c}} {x - {x_0}}\\ {y - {y_0}}\\ { - f} \end{array}} \right] = k{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{R}}_1^{\rm{T}}\left[ {\begin{array}{*{20}{c}} {X - \left( {{X_{{s_1}}} + \Delta X} \right)}\\ {Y - \left( {{Y_{{s_1}}} + \Delta Y} \right)}\\ {Z - \left( {{Z_{{s_1}}} + \Delta Z} \right)} \end{array}} \right], $ | (6) |
其中,
| $ \left[ {\begin{array}{*{20}{c}} {x - {x_0}}\\ {y - {y_0}}\\ { - f} \end{array}} \right] = k\left( {{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{R}}_1^{\rm{T}}\left[ {\begin{array}{*{20}{c}} {X - {X_{{s_1}}}}\\ {Y - {Y_{{s_1}}}}\\ {Z - {Z_{{s_1}}}} \end{array}} \right] - {\mathit{\boldsymbol{M}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y}\\ {\Delta z} \end{array}} \right]} \right). $ | (7) |
对于每一对相片,旋转矩阵M和平移量(Δx, Δy, Δz)都保持不变。通过上述式子,每个右相机影像共线方程中的外方位元素可以用对应的左相机外方位元素以及旋转矩阵M和平移量(Δx, Δy, Δz)转换得到。实际的平差计算中,对于左相机的误差模型采用原始的共线方程,对于右相机的误差模型采用本文推导的方程。
3 实验验证及分析首先对影像进行特征点提取和同名像点匹配。试验采用的尺度不变特征变换(Scale-Invariant Feature Transform, SIFT)算子[8]是用于图像处理领域的一种描述,对旋转、尺度缩放、亮度变化保持不变,对视角变化、仿射变换、噪声也具有一定的稳定性。一般来说,尺度不变特征变换算子的计算结果存在一定数量的误匹配点,本文对匹配结果使用随机抽样一致性算法进一步筛选,最终嫦娥三号巡视器环拍数据选取其中54对影像,共提取42 085个匹配点,嫦娥五号科学验证试验数据选取其中75对影像,共提取141 498个匹配点。
由于光束法平差属于非线性优化,需要提供未知数的初始值。在地球平台,通常可以通过全球定位系统测量和计算接收机载体的运动方位信息[9]。但是在深空探测领域,由于客观因素的制约,直接获取的相机外方位元素精度较低,不能作为平差计算的初始值。本文利用计算机视觉领域的运动恢复结构问题(Structure From Motion, SFM)的相关理论,根据匹配结果使用五点法计算本质矩阵,再用矩阵分解法分解该矩阵得到相机外方位元素的估算值,最后利用基于共线方程的前方交会方法估算像点对应的物方三维坐标。
相机镜头畸变模型采用布朗(brown)模型,只考虑径向畸变的部分,误差模型如下:
| $ {\Delta x = - x\left( {{k_0} + {k_1}{r^2} + {k_2}{r^4}} \right), } $ | (8) |
| $ {\Delta y = - y\left( {{k_0} + {k_1}{r^2} + {k_2}{r^4}} \right), } $ | (9) |
其中,
误差模型中未知数与观测值为非线性关系,故先对方程进行线性化,采用泰勒级数展开并保留一次项,然后采用经典的高斯-牛顿法(Gauss-Newton)进行迭代求解[10]。
考虑到迭代计算可能存在粗差的影响,本文加入了Huber loss函数,该函数是一种常用的鲁棒的回归损失函数,具体形式如下:
| $ {L_\delta }(a) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2}{a^2},|a| < \delta }\\ {\delta \left( {|a| - \frac{1}{2}\delta } \right),其他情况} \end{array} \ \ \ \ \ \ \ ,} \right. $ | (10) |
其中,a为误差方程算出的残差值;δ为函数的参数,可以根据具体残差的大小给定。
利用嫦娥五号数据对δ的取值进行实验,最终通过对比结果选取δ=1.0,即观测点反投影残差大于1个像素时,减弱其对整体误差的影响。
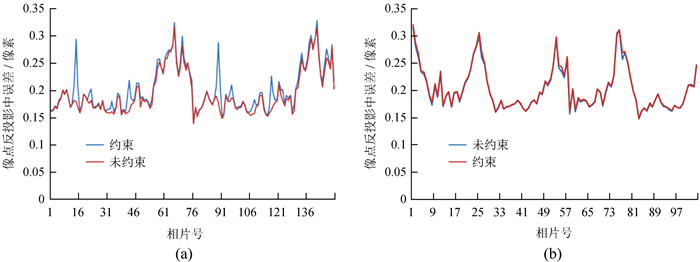
对试验数据分别进行了附加相对约束关系和未附加相对约束关系的平差计算,并统计了平差计算的相关数据,结果见表 2。另外,通过共线方程计算像点反投影的残差,并将像点中误差以影像为单位进行统计,两种方法得到结果的像点残差分布规律如图 6。
| 实验数据 | 是否附加相对 约束关系 | 迭代 次数 | 外方位元素 未知数个数 | 连接点中 误差/像素 | 连接点最大 误差/像素 |
| 嫦娥五号科学验证试验数据 | 是 | 6 | 456 | 0.207 | 2.974 |
| 否 | 7 | 900 | 0.199 | 2.743 | |
| 嫦娥三号巡视器环拍数据 | 是 | 5 | 330 | 0.191 | 2.925 |
| 否 | 4 | 648 | 0.190 | 2.903 |
|
| 图 6 平差结果像点中误差统计。(a)嫦娥五号数据处理结果;(b)嫦娥三号数据处理结果 Fig. 6 RMS statistics of points of adjustment results |
从以上的统计结果可以看出,两种方法得到结果的像点反投影误差规律非常接近,而在未知数个数方面,附加相对约束关系的平差方法能够减少部分外方位元素,对于节约计算机内存具有一定意义。
通过平差计算得到的影像外方位元素反求左右相机的相对姿态,转角系统按照x-y-z轴的顺序,3个旋转角分别为ω, ϕ, κ,统计了3个转角的平均值、中误差、最大误差等,结果见表 3。通过相机的外方位线元素求取左右相机间的距离,并统计了相关的误差指标,结果见表 4。
| 实验数据 | 是否附加 相对约束 关系 | ω / ° | ϕ / ° | κ / ° | ||||||||
| 平均值 | 中误差 | 最大 误差 | 平均值 | 中误差 | 最大 误差 | 平均值 | 中误差 | 最大 误差 | ||||
| 嫦娥五号科学 | 是 | 0.084 | 0 | 0 | 6.917 | 0 | 0 | 0.044 | 0 | 0 | ||
| 验证试验数据 | 否 | 0.078 | 0.007 | 0.025 | 6.917 | 0.009 | 0.029 | 0.045 | 0.001 | 0.005 | ||
| 嫦娥三号巡视 | 是 | 0.133 | 0 | 0 | 1.987 | 0 | 0 | -0.039 | 0 | 0 | ||
| 器环拍数据 | 否 | 0.134 | 0.006 | 0.019 | 1.990 | 0.003 | 0.011 | -0.040 | 0.003 | 0.010 | ||
| 实验数据 | 是否附加相对约束关系 | 立体像对距离 | |
| 平均值/m | 最大误差/m | ||
| 嫦娥五号科学验证试验数据 | 是 | 0.254 | 0 |
| 否 | 0.254 | 0.002 | |
| 嫦娥三号巡视器环拍数据 | 是 | 0.268 | 0 |
| 否 | 0.269 | 0.003 | |
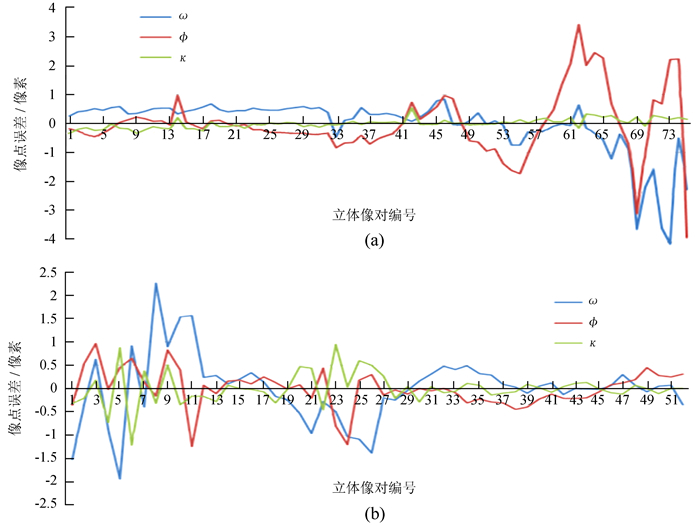
表 3和表 4显示,附加相对约束关系的平差方法能够确保模型内部的刚性关系,而传统方法由于是完全自由平差,在这方面产生一定误差,为了估算该误差产生的影响,利用瞬时视场角对其进行估算,两组实验数据的全景相机焦距约为50 mm,像元大小为7.4 μm,取两者比值得到瞬时视场角约为0.148 mrad,再通过与旋转角的误差值取比值,可以估算得出立体像对相对旋转角误差造成的像点误差大小,最后以像对为单位进行统计,结果如图 7。
|
| 图 7 相对姿态误差导致的像点误差分布情况。(a)嫦娥五号数据处理结果;(b)嫦娥三号数据处理结果 Fig. 7 Distribution of image point error caused by inaccurate relative pose |
由图 7可以看出,嫦娥五号科学验证试验数据的处理结果中,像点误差约为1个像素,最大超过3个像素,嫦娥三号巡视器全景相机环拍数据的处理结果中,像点误差约为1个像素,最大超过2个像素。相对姿态误差导致的像点误差达到了像素级别,对于最终解算得到的三维坐标必然会产生一定影响。
最后利用附加相对约束关系的平差结果对影像数据进行了密集匹配,通过前方交会的计算方法得到像点对应的物方三维坐标,并生成影像区域的三维模型。这部分内容借助软件Smart 3D完成,结果如图 8、图 9。

|
| 图 8 嫦娥五号全景相机科学验证试验外场区域三维模型 Fig. 8 3D model of outfield for scientific verification test of panoramic cameras in Chang′E-5 |

|
| 图 9 嫦娥三号巡视器月表环拍区域三维模型 Fig. 9 3D model of lunar surface around Chang′E-3 rover |
本文分析了当前月表双目立体相机平差处理存在的问题,参考了计算机视觉和航空摄影测量领域的处理经验后使用一种改进的平差模型,利用嫦娥五号科学验证试验数据和嫦娥三号巡视器环拍数据进行了验证。通过结果比较证明,本文使用的方法能够确保不同立体像对之间的相对外方位元素保持一致,提高左右相机间的内部吻合精度,得到的平差结果更加可靠。另外,该方法还能减少部分外方位元素未知数,在节约计算机内存方面有一定意义。因此,本文提出的平差方法可以应用于相关的月表影像处理工作,为后续的研究提供支持。
| [1] | 薛喜平, 张洪波, 孔德庆. 深空探测天文自主导航技术综述[J]. 天文研究与技术, 2017, 14(3): 382–391 |
| [2] | 张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2009. |
| [3] | 邸凯昌. 火星车定位与制图技术现状以及对发展中国月球车/火星车定位制图技术的建议[J]. 遥感学报, 2009, 13(增刊1): 101–112 |
| [4] | WANG W R, REN X, WANG F F, et al. Terrain reconstruction from Chang'e-3 PCAM images[J]. Research in Astronomy and Astrophysics, 2015, 15(7): 1057–1066. DOI: 10.1088/1674-4527/15/7/013 |
| [5] | EBNER H, KORNUS W, OHLHOF T. A simulation study on point determination for the MOMS-02/D2 space project using an extended functional model[J]. International Archives of Photogrammetry and Remote Sensing, 1992, 29(B4): 458–464. |
| [6] | 闫利, 费亮, 叶志云, 等. 大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317 |
| [7] | 张力, 艾海滨, 许彪, 等. 基于多视影像匹配模型的倾斜航空影像自动连接点提取及区域网平差方法[J]. 测绘学报, 2017, 46(5): 554–564 |
| [8] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI: 10.1023/B:VISI.0000029664.99615.94 |
| [9] | 李佳威, 李芳, 何瑞珠. 利用GPS测速估算接收机载体运动方位角[J]. 天文研究与技术, 2017, 14(1): 45–51 |
| [10] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002. |



