2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
全球导航卫星系统(Global Navigation Satellite System, GNSS)卫星定位误差分析中,主要使用测距误差均一假设下的定位误差模型,即当卫星的测距误差满足相互独立和方差均一的同分布条件时,定位误差等于测距误差标准差与几何精度因子(Geometric Dilution of Precision, GDOP)的乘积[1]。几何精度因子仅与卫星的几何分布有关,它与用户接收机和可视卫星形成的四面体或多面体的体积成反比[2]。有很多研究工作致力于参与定位选星工作,以得到尽可能小的几何精度因子值[2-4]。测距误差是对卫星伪距测量值进行误差校正后得到的伪距测量误差量,其中包含未剔除干净的对流层延迟、电离层延迟、多径干扰与接收机噪声等误差项。实际定位解算中,由于卫星间的相互差异、传播路径不同等因素,不同卫星测距误差的统计特征难以相同,无法满足方差均一的条件[5]。尤其当某颗卫星信号受到多径效应或电离层闪烁影响时,其测距误差显著增大[6-8]。围绕多径干扰、电离层闪烁与定位误差间的关系展开了很多研究工作,有研究给出统计分析和试验结果,说明了多径干扰、电离层闪烁对定位误差存在影响[6-8],但尚未给出统一的结论描述多径效应、电离层闪烁与定位误差之间的关系。有研究提议剔除测距误差大的卫星,但这样做改变了卫星的星座分布,可能会恶化几何精度因子[9],该措施对定位精度的维持起一定作用,但对于一般的用户接收机并不实用。因此,在测距误差非均一的实际定位解算中,尤其当卫星信号受到多径干扰或电离层闪烁影响时,如何保证卫星导航定位精度,如何在一般用户接收机中实施,需要考察非均一测距误差如何影响定位精度。已有研究针对全球定位系统定位考察了非均一伪距误差对定位误差的影响,给出了定位误差模型[10]。
本文旨在对卫星测距误差非均一时的定位误差模型进行验证。首先利用奇异值分解(Singular Value Decomposition, SVD)方法对几何矩阵进行分解,推导出定位误差协方差表达式,给出定位误差模型。接下来利用北京站与香港站的实测数据,对受到多径效应与电离层闪烁影响的卫星信号进行定位解算,将定位结果与非均一测距误差下的理论模型进行对比和分析。最后给出了结论。
1 基于奇异值分解方法的定位误差模型在线性代数中,奇异值分解是分解矩阵的基本方法,利用奇异值分解方法求解方程在理论上与最小二乘法是完全等效的。奇异值分解的优势在于它能够给出矩阵的伪逆,从而推导出解的简洁、自约束的表达式,从奇异值分解中得到的奇异值和正交向量可以洞察问题的几何与理论内涵。并且奇异值分解求解具有数值稳定性,相比易受舍入误差影响且方程自身奇异的最小二乘解,奇异值分解方法解决了舍入问题,它是最小二乘法意义下的最优近似解。
全球导航卫星系统定位中,定位误差方程可表示为
| $ {\delta _{\rm{ \mathit{ ρ} }}} = \mathit{\boldsymbol{G}}\left[ {\begin{array}{*{20}{c}} {\delta x}\\ {\delta y}\\ {\delta z}\\ {\delta b} \end{array}} \right] + {\varepsilon _{\rm{p}}}, $ | (1) |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} { - e_x^{(1)}}&{ - e_y^{(1)}}&{ - e_z^{(1)}}&1\\ { - e_x^{(2)}}&{ - e_y^{(2)}}&{ - e_z^{(2)}}&1\\ \vdots & \vdots & \vdots & \vdots \\ { - e_x^{(n)}}&{ - e_y^{(n)}}&{ - e_z^{(n)}}&1 \end{array}} \right]. $ | (2) |
其中,δρ和ερ分别表示卫星伪距测量值与估测值之差和测距误差;[δx δy δz δb]T为用户接收机位置与钟差的未知修正量;G为几何矩阵。利用奇异值分解方法对几何矩阵G进行分解,可推导出定位误差协方差表达式,给出定位误差模型。
用奇异值分解方法对几何矩阵G进行分解:
| $ \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{U}}diag\left( {{\omega _i}} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}, $ | (3) |
G矩阵的伪逆为
| $ {\mathit{\boldsymbol{G}}^ + } = \mathit{\boldsymbol{V}}diag\left( {{\lambda _i}} \right){\mathit{\boldsymbol{U}}^{\rm{T}}}, {\lambda _i} = 1/{\omega _i}, $ | (4) |
其中,
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{U_{11}}}&{{U_{12}}}&{{U_{13}}}&{{U_{14}}}\\ {{U_{21}}}&{{U_{22}}}&{{U_{23}}}&{{U_{24}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{U_{N1}}}&{{U_{N2}}}&{{U_{N3}}}&{{U_{N4}}} \end{array}} \right], $ | (5) |
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{l}} {{V_{x1}}}&{{V_{x2}}}&{{V_{x3}}}&{{V_{x4}}}\\ {{V_{y1}}}&{{V_{y2}}}&{{V_{y3}}}&{{V_{y4}}}\\ {{V_{z1}}}&{{V_{z2}}}&{{V_{z3}}}&{{V_{z4}}}\\ {{V_{b1}}}&{{V_{b2}}}&{{V_{b3}}}&{{U_{N4}}} \end{array}} \right], $ | (6) |
U和V是正交矩阵,U的列向量和V的列向量分别是GGT与GTG的特征向量;diag(ωi)和diag(λi)是4 × 4的对角阵;ωi和λi(i=1, 2, 3, 4)分别是G和G+的奇异值,ω1≤ ω2≤ ω3≤ ω4,λ1≥λ2≥λ3≥λ4。
用εr表示定位误差,定位误差协方差可表示为
| $ Cov\left( {{\varepsilon _{\rm{r}}}} \right) = {\mathit{\boldsymbol{G}}^ + }\mathit{\boldsymbol{E}}\left( {{\varepsilon _{\rm{ \mathit{ ρ} }}}\mathit{\varepsilon }_{\rm{ \mathit{ ρ} }}^{\rm{T}}} \right){\left( {{\mathit{\boldsymbol{G}}^ + }} \right)^{\rm{T}}} = \mathit{\boldsymbol{V}}diag\left( {{\lambda _i}} \right){\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{E}}\left( {{\varepsilon _{\rm{ \mathit{ ρ} }}}\mathit{\varepsilon }_{\rm{ \mathit{ ρ} }}^{\rm{T}}} \right)\mathit{\boldsymbol{U}}diag\left( {{\omega _i}} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}. $ | (7) |
卫星的测距误差服从独立、零均值并具有相同方差的正态分布时,测距误差模型特性如下:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{E}}\left( {{\varepsilon _{\rm{ \mathit{ ρ} }}}} \right) = 0, }\\ {Cov\left( {{\varepsilon _{\rm{ \mathit{ ρ} }}}} \right) = \sigma _0^2{I_{N \times N}}, }\\ {\mathit{\boldsymbol{E}}\left( {\varepsilon _{\rm{ \mathit{ ρ} }}^{\left( i \right)}\varepsilon _{\rm{ \mathit{ ρ} }}^{\left( j \right)}} \right) = 0, i \ne j, } \end{array} $ | (8) |
其中,σ02为卫星的测距误差的方差。由(7)式可得定位误差的协方差矩阵:
| $ Cov\left( {{\varepsilon _{\rm{r}}}} \right) = \mathit{\boldsymbol{V}}diag\left( {\lambda _i^2} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}_0^2. $ | (9) |
该矩阵为一实对称矩阵,可表示为Hσ02,H=(GTG)-1为几何精度因子矩阵。因此,
| $ \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{V}}diag\left( {\lambda _i^2} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}, $ | (10) |
V的4个列向量(V1 V2 V3 V4)是矩阵H的特征向量,λ12≥λ22≥λ32≥λ42是H的4个特征值。定位误差的分布是一个四维椭球,(V1 V2 V3 V4)定义了误差椭球4个主轴的方向,V1是主轴,σ0λ1, σ0λ2, σ0λ3, σ0λ4是椭球的半轴长[10]。
1.2 基于奇异值分解方法的非均一方差定位误差模型当卫星的测距误差无法满足具有相同方差的正态分布条件时,用σn2表示第n颗卫星的测距误差方差,测距误差模型特性如下:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{E}}\left( {{\varepsilon _{\rm{ \mathit{ ρ} }}}} \right) = 0, }\\ {\mathit{Cov}\left( {{\varepsilon _{\rm{ \mathit{ ρ} }}}} \right) = diag\left( {\sigma _n^2} \right), n = 1, 2, \cdots , N, }\\ {\mathit{\boldsymbol{E}}\left( {\varepsilon _{\rm{ \mathit{ ρ} }}^{(i)}\varepsilon _{\rm{ \mathit{ ρ} }}^{(j)}} \right) = 0, \;i \ne j.} \end{array} $ | (11) |
由(7)式可得定位误差的协方差矩阵:
| $ \mathit{Cov}\left( {{\varepsilon _{\rm{r}}}} \right) = \mathit{\boldsymbol{V}}diag\left( {{\lambda _i}} \right){\mathit{\boldsymbol{U}}^{\rm{T}}}diag\left( {\sigma _n^2} \right)\mathit{\boldsymbol{U}}diag\left( {{\omega _i}} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}, \;\;\;\;i = 1, 2, 3, 4;n = 1, 2, \cdots , N. $ | (12) |
可以看出,在卫星测距误差非均一的情况下,定位误差模型更加复杂。
假设n颗卫星中测距误差方差最小为σ02,σn2≥σ02,将(12)式中的定位误差协方差矩阵展开,可得总的定位误差协方差矩阵Cov(εr)T[10]:
| $ \mathit{Cov}{\left( {{\varepsilon _{\rm{r}}}} \right)_{\rm{T}}} = \mathit{\boldsymbol{V}}diag\left( {\lambda _i^2} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}\sigma _0^2 + \sum\limits_{n = 1}^N {\mathit{\boldsymbol{V}}diag\left( {{\lambda _i}} \right)\left[ {\begin{array}{*{20}{c}} {{u_{n1}}}\\ {{u_{n2}}}\\ {{u_{n3}}}\\ {{u_{n4}}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{u_{n1}}}\\ {{u_{n2}}}\\ {{u_{n3}}}\\ {{u_{n4}}} \end{array}} \right]}^{\rm{T}}}diag\left( {{\lambda _i}} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}\left( {\sigma _n^2 - \sigma _0^2} \right)} . $ | (13) |
Cov(εr)T由同方差性定位误差与测距误差方差增量带来的定位误差增量总和两部分组成。Cov(εr)T不仅与V,λi2,σ02有关,还与测距误差方差增量σn2-σ02和U矩阵中第n行向量有关。
从(13)式可以看出,Cov(εr)T是一个实对称矩阵。用VT的4个列向量表示Cov(εr)T的特征向量,ξT12, ξT22, ξT32, ξT42表示Cov(εr)T的特征值。根据矩阵特征值交织定理,ξTi2与λi2σ02关系如下:
| $ \begin{array}{*{20}{c}} {\xi _{{\rm{TI}}}^2 \ge \lambda _1^2\sigma _0^2 \ge \xi _{{\rm{T}}2}^2 \ge \lambda _2^2\sigma _0^2 \ge \xi _{{\rm{T}}3}^2 \ge \lambda _3^2\sigma _0^2 \ge \xi _{{\rm{T}}4}^2 \ge \lambda _4^2\sigma _0^2, }\\ {\sum\limits_{i = 1}^4 {\xi _{{\rm{T}}i}^2} = \sum\limits_{i = 1}^4 {\lambda _i^2} \sigma _0^2 + \sum\limits_{n = 1}^N {\lambda _{zn}^2} \left( {\sigma _n^2 - \sigma _0^2} \right), } \end{array} $ | (14) |
其中,
| $ \begin{array}{l} {\lambda _{zn}} = \sqrt {{{\left( {\sum\limits_{i = 1}^4 {{\lambda _i}} {u_{ni}}{V_{xi}}} \right)}^2} + {{\left( {\sum\limits_{i = 1}^4 {{\lambda _i}} {u_{ni}}{V_{yi}}} \right)}^2} + {{\left( {\sum\limits_{i = 1}^4 {{\lambda _i}} {u_{ni}}{V_{zi}}} \right)}^2} + {{\left( {\sum\limits_{i = 1}^4 {{\lambda _i}} {u_{ni}}{V_{bi}}} \right)}^2}} , \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{Z_{nx}} = \left( {\sum\limits_{i = 1}^4 {{\lambda _i}{u_{ni}}{V_{xi}}} } \right)/{\lambda _{zn}}, }&{{Z_{ny}} = \left( {\sum\limits_{i = 1}^4 {{\lambda _i}{u_{ni}}{V_{yi}}} } \right)/{\lambda _{zn}}, }\\ {{Z_{nz}} = \left( {\sum\limits_{i = 1}^4 {{\lambda _i}} {u_{ni}}{V_{zi}}} \right)/{\lambda _{zn}}, }&{{Z_{nb}} = \left( {\sum\limits_{i = 1}^4 {{\lambda _i}} {u_{ni}}{V_{bi}}} \right)/{\lambda _{sn}}.} \end{array} \end{array} $ | (15) |
定位误差协方差矩阵可用特征值与特征向量表示为
| $ Cov{\left( {{\varepsilon _{\rm{r}}}} \right)_{\rm{T}}} = {\mathit{\boldsymbol{V}}_{\rm{T}}}diag\left( {\xi _{{\rm{T}}i}^2} \right)\mathit{\boldsymbol{V}}_{\rm{T}}^{\rm{T}}. $ | (16) |
由此可知,当卫星测距误差非均一时,定位误差的分布是一个四维椭球,VT1, VT2, VT3, VT4定义椭球的4个主轴,VT1是主轴,ξT1, ξT2, ξT3, ξT4是椭球的半轴长。该椭球相比测距误差均一假设下的定位误差椭球,主轴朝一特定方向趋近,该方向与星座分布、测距误差方差增大的卫星的位置均有关[10]。误差椭球轴长因测距误差方差增量而增加,主轴增加的最多。当σn2远大于σ02时,ξT12将远大于λ12σ02,误差椭球主要沿主轴方向被拉长。所有卫星的测距误差方差增量将大大拉长定位误差椭球[10]。
2 基于奇异值分解方法的定位结果分析本文利用北京站与香港站的实测数据对基于奇异值分解的定位误差模型进行验证。选取卫星信号受到多径干扰和电离层闪烁影响时的数据进行定位解算, 此时卫星测距误差显著增大,根据定位误差模型,定位误差椭球主轴将明显偏转拉长。
首先对卫星伪距进行拟合去趋势处理得到卫星测距误差。接下来利用奇异值分解方法对受到多径干扰与电离层闪烁影响的卫星进行定位解算,得到实际定位结果。利用(9)式得到测距误差均一假设下定位误差椭球主轴的特征向量与特征值,利用(12)式和(16)式得到测距误差非均一情况下实际定位误差椭球主轴的特征向量与特征值,通过对比定位误差椭球的特征向量特征值与实际定位结果,验证定位误差椭球模型的正确性。
2.1 定位解算参数(1) 地点坐标
选择国际GPS服务(International GNSS Service, IGS)站中北京站BJFS与香港站HKSL两个地点,分别考察多径效应和电离层闪烁对定位误差的影响。北京站的坐标为39°54′50″ N,116°23′30″ E,香港站的坐标为22°22′19″ N,113°55′40″ E。香港站处于低纬地区,电离层闪烁事件发生频繁。
(2) 卫星位置与伪距测量值
利用2014年4月25~27日、2014年3月20~22日、2014年6月20~22日、2014年9月22~24日、2014年12月21~23日、2014年2月27日、2014年3月10日的全球定位系统卫星实测数据进行定位解算。伪距测量值与卫星位置由IGS网站提供的采样率为30 s观测文件与导航电文获得。
2.2 测距误差提取方法伪距测量值包含各种误差,按照来源不同大致可分为3方面:与卫星有关的误差、与信号传播有关的误差及与接收机有关的误差。测量误差的两个重要特征是其大小和变化快慢,根据变化快慢这个特征,上述各种误差可以分为偏差和噪声两类。偏差是指在一段时间内变化较慢的误差。偏差量的大小具有一定稳定性,可直接测量或者用数学模型预测。与偏差相反,噪声是变化很快的一类误差,具有统计特征,具体值很难预测。
观测文件中记录了卫星的伪距观测值,可知卫星伪距变化存在一定趋势,趋势中包含卫星到接收机的几何距离和伪距测量偏差。对卫星伪距随时间变化曲线进行去趋势处理,得到的残差项即是测距误差εp。
利用多项式拟合对卫星伪距随时间变化曲线进行拟合去趋势处理,用均方根和系数R确定多项式系数,实现去趋势后测距误差最准确。
2.2.1 多径效应对测距误差的影响多径效应是指接收机天线接收到全球定位系统信号经周围地物反射后的信号,而每个反射信号又可能经过一次或多次反射后到达天线。多径效应会降低载波相位以及伪距的测量精度,严重时还可以导致码相位失锁和卫星信号失踪。一般来说,低仰角卫星信号更容易发生多径现象。即卫星仰角越小,多径效应发生的概率越大,伪距测量精度越低,测距误差越大,σn越大。
图 1为2014年4月26日北京站测得的PRN14、15、18、21、22、24共6颗卫星24小时内测距误差标准差σn随仰角变化图。设置卫星仰角截止角为10°。从图 1可以看出,随着仰角变小,卫星信号受多径效应影响,σn由0.25 m变大到2 m。可通过仰角大小判断卫星信号测距误差是否受到多径效应的影响。
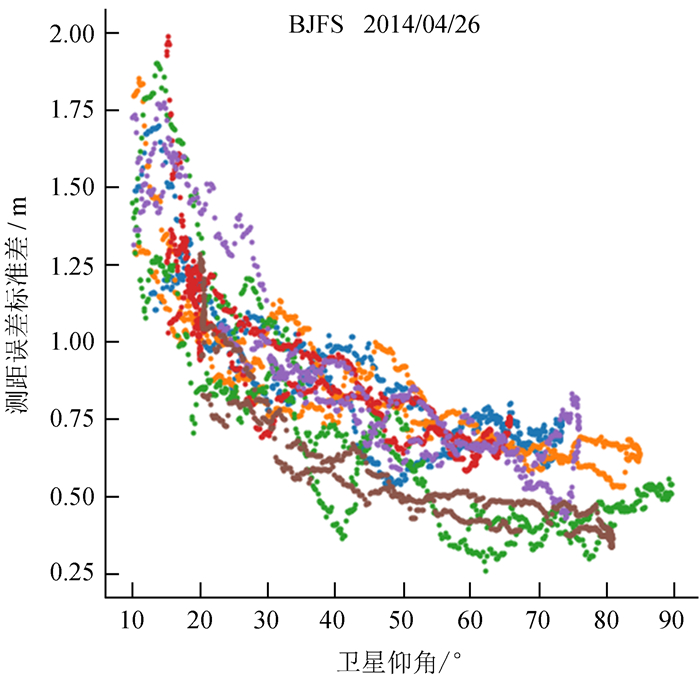
|
| 图 1 测距误差标准差随仰角变化 Fig. 1 σn elevation-varying graph |
电离层闪烁导致电离层中传播的无线电信号快速起伏,严重时引起信号的中断,是影响空间无线电系统性能的重要因素。低纬的赤道异常区是全球范围内电离层闪烁出现最频繁、影响最严重的地区之一[8]。电离层闪烁可以引起用户接收机测量误差增大[8]。
电离层电子密度总量(Total Electron Content, TEC)变化率指数(Rate of TEC Index, ROTI)越大,闪烁现象越严重[11]。图 2给出了2014年3月香港站受电离层闪烁影响卫星的测距误差标准差σn随ROTI的变化情况。由图 2可见,σn在0.2 m至3 m之间变化,且随着ROTI值的增大,σn呈增大趋势。可通过ROTI值判断卫星信号测距误差是否受到电离层闪烁的影响。
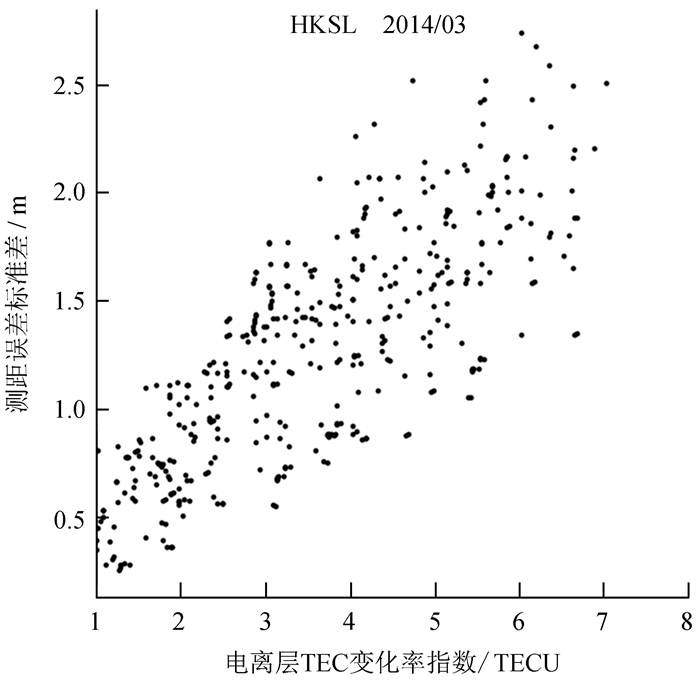
|
| 图 2 测距误差标准差随ROTI变化 Fig. 2 σn ROTI-varying graph |
在实测数据中,卫星星座分布随时间变化,选择在一定时间段内星座分布变化较小的数据对定位误差模型进行验证。2014年4月25~27日,每日0: 20~0: 35 (历元40~70),北京站可视卫星的方位角与仰角变化范围小于5°,星座分布基本一致。设置卫星仰角截止角为10°,卫星仰角在10°到30°之间时,卫星受多径效应影响。0: 20~0: 35视野中有PRN14、15、18、21、22、24共6颗卫星,有且仅有PRN14一颗卫星受到多径效应影响。图 3给出了2014年4月26日视野内每颗卫星全天的σn随时间变化曲线。可见,在实际定位中,卫星测距误差是非均一的,当卫星受到多径干扰时,σn显著增大。
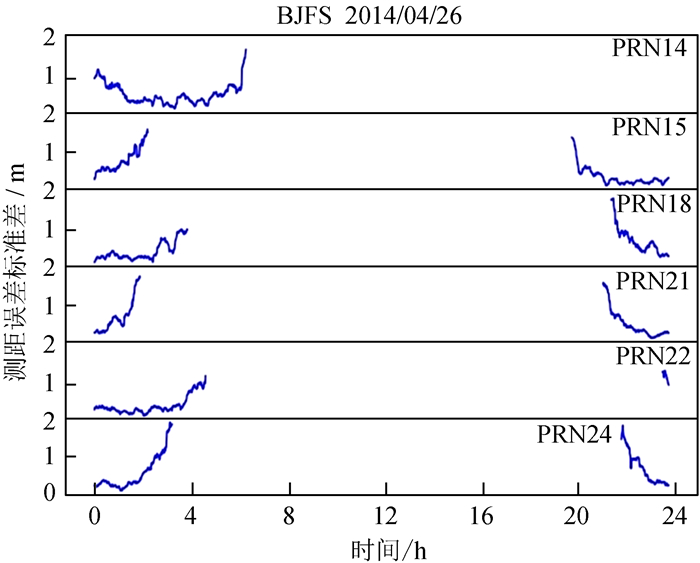
|
| 图 3 2014年4月26日卫星测距误差标准差随时间变化 Fig. 3 σn time-varying curve on April 26, 2014星受到多径干扰时, σn显著增大。 |
在站心坐标系下进行定位解算,坐标系中E-N方向为水平方向。坐标原点(0, 0)代表接收机位置,x轴正向代表接收机东向,y轴正向代表接收机北向。定位点与实际接收机位置的偏差,即定位误差(Positioning Error)。图 4为2014年4月25~27日北京站定位结果在水平方向上投影的分布图。
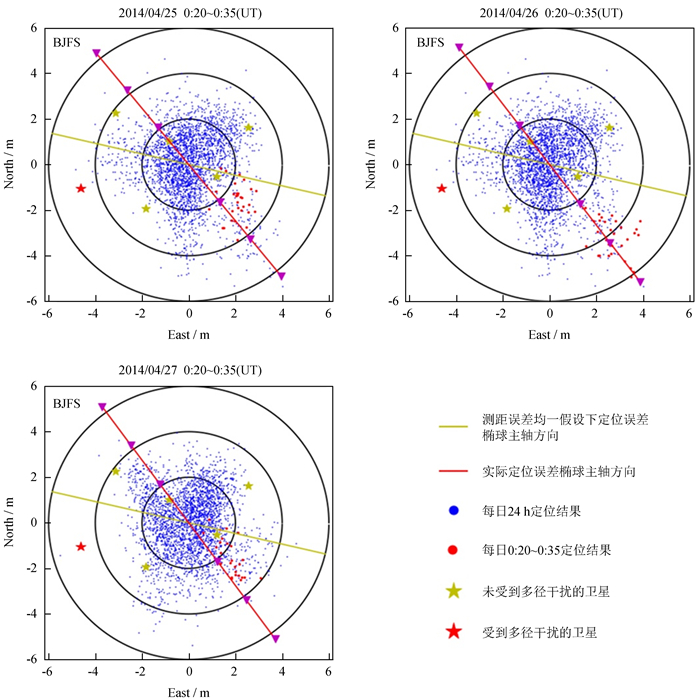
|
| 图 4 2014年4月25日、26日、27日北京站定位结果分布 Fig. 4 Positioning of BJFS on April 25, 2014, April 26, 2014, April 27, 2014 |
将0: 20~0: 35的30个水平方向定位结果用红点标出,全天24小时内2 880个定位结果用蓝点标出。图中卫星仰角60°,30°,0°分别对应半径为2 m,4 m,6 m的圆,卫星方位角与定位误差方位对应。将受到多径干扰的PRN14号卫星15分钟内的方位角与仰角均值用红色星形标出,其他星均由黄色星形表示。
30个定位结果对应30个几何矩阵。对矩阵进行奇异值分解,得到每一历元测距误差均一假设下定位误差椭球主轴的特征向量V1和特征值λ1。将V 1均值
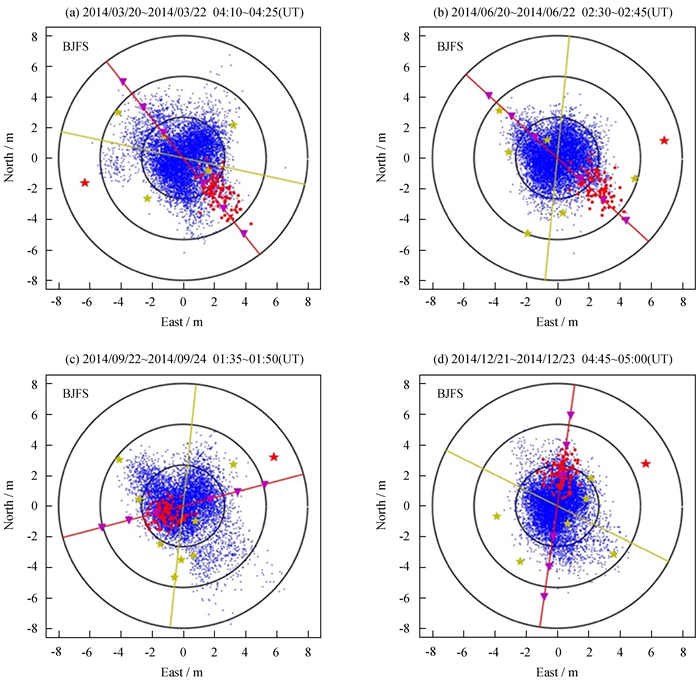
图 5给出了2014年春分、夏至、秋分、冬至及其前后两天北京站水平方向的定位分布。图 5 (a)、图 5 (b)、图 5 (c)、图 5 (d)分别由2014年3月20日~22日每日04: 10~04: 25、2014年6月20日~22日每日02: 30~02: 45、2014年9月22日~24日每日01: 35~01: 50、2014年12月21日~23日每日04: 45~05: 00的定位结果构成。图中卫星仰角60°,30°,0°分别对应半径为8/3 m,16/3 m,8 m的圆,卫星方位角与定位误差方位对应。
|
| 图 5 春分、夏至、秋分、冬至北京站定位结果 Fig. 5 Positioning of BJFS on 2014-03-20~22, 2014-06-20~22, 2014-09-22~24, 2014-12-21~23 |
表 1给出了2014年3月21日04: 10~04: 25、2014年4月26日0:20~0:35、2014年6月21日02: 30~02: 45、2014年9月23日01: 35~01: 50、2014年12月22日04: 45~05: 00每日30个历元内的几何精度因子均值,测距误差方差增量均值
| 日期 | 时间 | 几何精度因子均值 /m |
测距误差方差增量均值 /m |
测距误差均一假设下定位误差椭球主轴半轴长均值的投影值/m | 实际定位误差椭球主轴半轴长均值的投影值/m |
| 2014-03-21 | 04:10~04:25 | 3.594 | 2.587 | 0.470 | 2.078 |
| 2014-04-26 | 0:20~0:35 | 3.598 | 2.655 | 0.495 | 2.092 |
| 2014-06-21 | 02:30~02:45 | 2.707 | 4.811 | 0.396 | 1.937 |
| 2014-09-23 | 01:35~01:50 | 2.654 | 3.495 | 0.417 | 1.822 |
| 2014-12-22 | 04:45~05:00 | 2.853 | 2.875 | 0.447 | 1.986 |
结合图 4、图 5、表 1可以看出,实际定位结果与非均一方差定位误差模型基本吻合。在轴方向上,实际定位误差椭球主轴方向相比测距误差均一假设下的误差椭球主轴方向明显旋转,旋转角度与星座分布、σn增大和卫星位置有关,所选时间段内的定位点基本分布在实际定位误差椭球主轴方向的周围。对于轴长,实际定位误差椭球轴长相比测距误差均一假设下的误差椭球轴长明显增大,增大量与星座分布和测距误差方差增量有关,实际定位结果分布在3
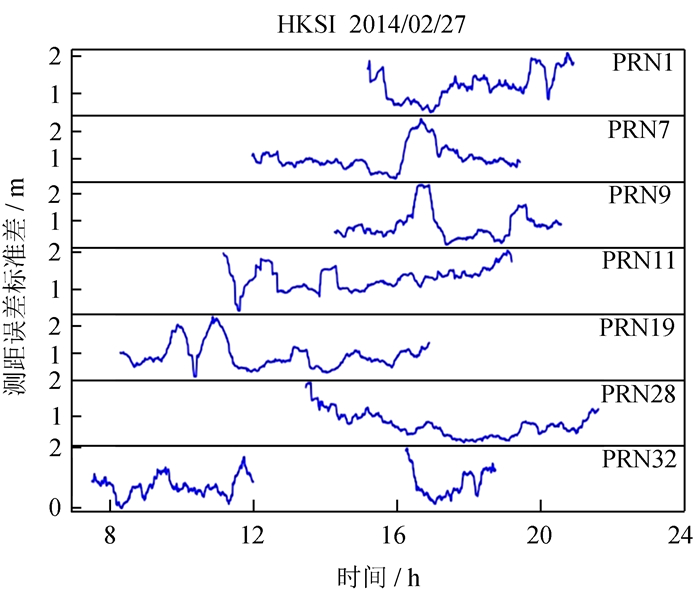
通过ROTI值可以判断卫星信号是否受电离层闪烁的影响。根据计算结果得知,2014年2月27日16: 00~17: 00 PRN7号、9号卫星与2014年3月10日18: 00~19: 00 PRN7号卫星均受到较强的电离层闪烁的影响。其中,2014年2月27日16: 25~16: 40卫星星座变化较小,此时视野内有PRN1、7、9、11、19、28、32共7颗卫星,其中PRN19、32号卫星受到多径干扰,PRN7号、9号卫星受到电离层闪烁影响。
图 6给出了2014年2月27日这7颗卫星的测距误差标准差随时间变化的曲线。由图 6可见,当卫星信号受到多径干扰或电离层闪烁影响时,σn明显增大。
|
| 图 6 2014年2月27日香港站卫星测距误差标准差随时间的变化 Fig. 6 σn time-varying curve on Feb 27, 20 |
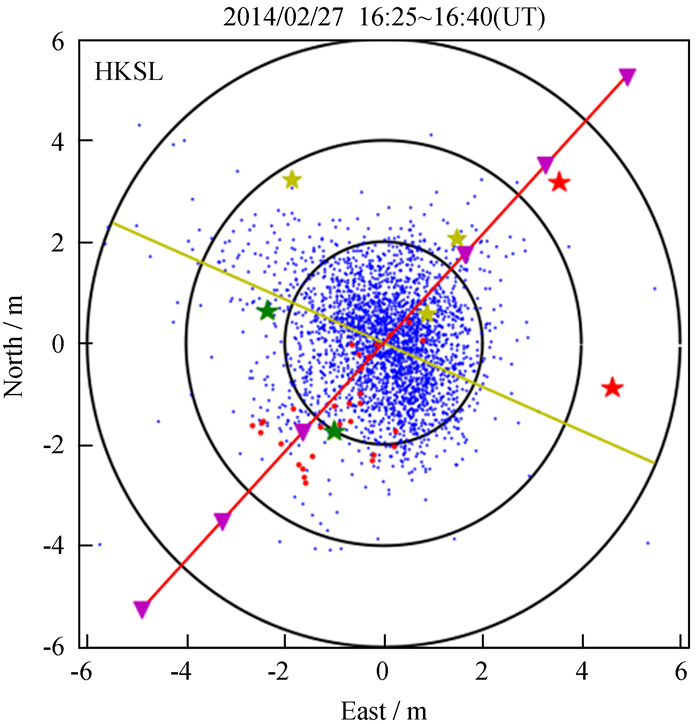
图 7为2014年2月27日香港站水平方向的定位结果分布图,蓝点标记全天的定位结果,红点标记16: 25~16: 40的定位结果。用红色星形标记受到多径干扰的PRN19号卫星与PRN32号卫星,用绿色星形标记受到电离层闪烁影响的PRN7号卫星与PRN9号卫星,其他星均由黄色星形标记。
|
| 图 7 2014年2月27日香港站定位结果 Fig. 7 Positioning of HKSL on Feb 27, 2014 |
经计算得,
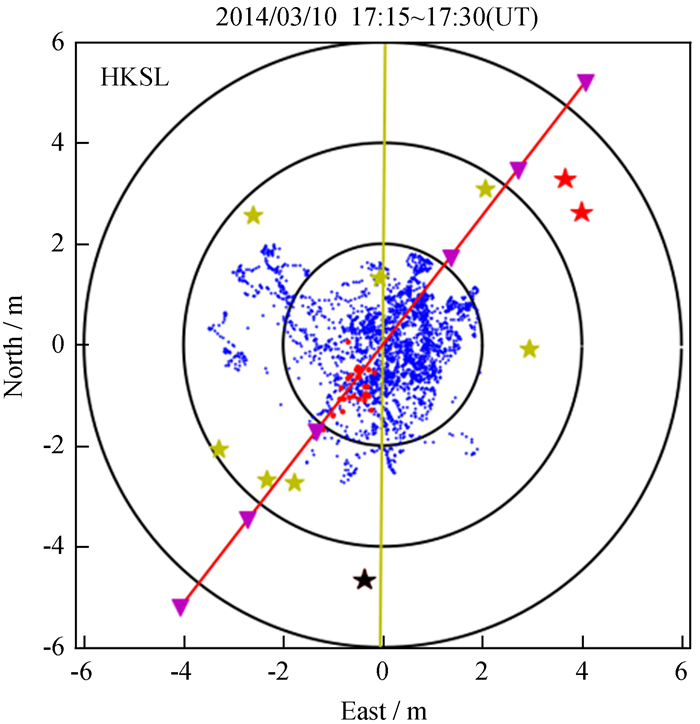
图 8为2014年3月10日香港站水平方向的定位结果分布图。17: 15~17: 30卫星星座变化较小,用红点标记这段时间内的定位结果。这段时间视野内有PRN1、4、7、8、9、11、17、20、28、32共10颗卫星。PRN7、11、32共3颗卫星受到多径干扰,其中PRN7号卫星在这段时间内既受到多径干扰又受到电离层闪烁影响,用黑色星形标记。经计算得,
|
| 图 8 2014年3月10日香港站定位结果 Fig. 8 Positioning of HKSL on Mar 10, 2014 |
结合定位分布图与计算结果可知,实际定位结果在轴向、轴长两方面均与非均一方差定位误差模型相吻合,且多颗卫星测距误差标准差均显著增大时,误差椭球主轴拉长更为明显。
3 结论本文对全球导航卫星系统测距误差非均一时的定位误差特性进行研究,利用奇异值分解方法给出了非均一方差定位误差模型。模型指出,当测距误差非均一时,定位误差在空间呈四维椭球分布,椭球的轴向和轴长可由对定位误差协方差矩阵进行奇异值分解获得。与测距误差均一假设下的定位误差椭球相比,测距误差非均一时,定位误差椭球因测距误差方差增量偏转拉长。当有卫星测距误差方差显著增大时,主轴偏转明显,椭球主要沿主轴被拉长。本文利用北京站与香港站的实测数据对模型进行检验。首先对卫星伪距进行拟合去趋势处理,提取卫星的测距误差,接着对受多径干扰和电离层闪烁影响的卫星进行定位解算分析。结果表明:卫星信号受到多径干扰或电离层闪烁影响时,测距误差标准差显著增大。此时实际定位误差椭球相较测距误差均一假设下的定位误差椭球,主轴方向明显旋转,主轴明显拉长。实际定位结果与非均一定位误差椭球主轴方向一致,分布范围与椭球主轴半轴长吻合。可见,非均一方差定位误差模型可以准确描述几何精度因子、测距误差与定位误差之间的关系,为进一步研究定位精度提供依据。
致谢: 感谢IGS网站提供GNSS实测数据;感谢中国科学院国家天文台李婧华老师在数据处理方面的支持与帮助。
| [1] | KAPLAN E, HEGARTY C. Understanding GPS:principles and applications[M]. Fitchburg: Artech House, 2006. |
| [2] | BLANCO-DELGADO N, NUNES F D, SECO-GRANADOS G. On the relation between GDOP and the volume described by the user-to-satellite unit vectors for GNSS positioning[J]. GPS Solutions, 2017, 21(3): 1139–1147. DOI: 10.1007/s10291-016-0592-3 |
| [3] | 徐小钧, 马利华, 艾国祥. 基于NSGA-Ⅱ算法的多目标快速选星方法[J]. 天文研究与技术, 2018, 15(3): 292–301 |
| [4] | ZHOU S S, CAO Y L, ZHOU J H, et al. Positioning accuracy assessment for the 4GEO/5IGSO/2MEO constellation of COMPASS[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(12): 2290–2299. DOI: 10.1007/s11433-012-4942-z |
| [5] | AWANGE J L, GRAFAREND E W. Algebraic solution of GPS pseudo-ranging equations[J]. GPS Solutions, 2002, 5(4): 20–32. DOI: 10.1007/PL00012909 |
| [6] | DONG D, WANG M, CHEN W, et al. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map[J]. Journal of Geodesy, 2016, 90(3): 255–262. DOI: 10.1007/s00190-015-0870-9 |
| [7] | JIA Q Q, WU R B, WANG W Y. Multipath interference mitigation in GNSS via WRELAX[J]. GPS Solutions, 2017, 21(2): 487–498. DOI: 10.1007/s10291-016-0538-9 |
| [8] | LINTY N, MINETTO A, DOVIS F, et al. Effects of phase scintillation on the GNSS positioning error during the September 2017 storm at Svalbard[J]. Space Weather, 2018, 16(9): 1317–1329. DOI: 10.1029/2018SW001940 |
| [9] | BALAEI A T, MOTELLA B, DEMPSTER A G. Mutual effects of satellite signal quality and satellite geometry on positioning quality[C]//20th International technical meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007). 2007: 1182-1190. |
| [10] | FAN J T, MA G Y. Characteristics of GPS positioning error with non-uniform pseudorange error[J]. GPS Solutions, 2014, 18(4): 615–623. DOI: 10.1007/s10291-013-0359-z |
| [11] | PI X C, MANNUCCI A J, LINDQWISTER U J, et al. Monitoring of global ionospheric irregularities using the worldwide GPS network[J]. Geophysical Research Letters, 1997, 24(18): 2283–2286. DOI: 10.1029/97GL02273 |


