2. 中国科学院射电天文重点实验室, 江苏 南京 210008;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210008, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
近年来随着天线向大口径、高频段方向发展,天线的指向精度作为重要的性能指标愈发受到关注。一般要求天线指向误差小于十分之一的波束宽度,但随着天线口径以及观测频率的增加,实现这一目标极具挑战,因此任何引起指向误差的因素都需要慎重考虑。
对于轮轨式方位俯仰型天线而言,轨道高差会引起天线在方位方向的运转偏差,引入轴系误差造成指向精度下降。早期的天线如上海25 m、新疆25 m射电望远镜均采用拼接轨道,天线运转过程中在轨道接缝处产生跳动引起天线方位偏差,拼接轨道在接缝处容易产生应力集中造成轨道寿命下降,因此拼接轨道多用于精度要求不高的场合。随着天线口径的增大、观测频段的提高,拼接方式已经无法满足要求。因此,全焊接的高精度轨道已经在一些大天线上得以运用,如美国绿岸100 m射电望远镜[1]、上海天马65 m射电望远镜[2]等。高精度轨道焊接技术随着轨道规模以及运用环境场合不同,其焊接工艺差别较大。以中国科学院新疆天文台即将建成的110 m全可动射电望远镜[3]为例,其指向精度要求1.5″,为了实现这一目标,轨道的精度要求控制在0.2 mm(峰峰值),同时天线运行在全年温差较大的高海拔地区,因此轨道的焊接将是新的挑战。
新疆天文台南山25 m射电望远镜于1993年建成,2015年完成升级改造。改造后天线口径26 m(如图 1)采用全焊接轨道技术,图 2为26 m射电望远镜的一段焊接头。在轨道焊接后及天线运行正常期间对轨道高差开展了3次测量,以验证轨道精度与可靠性。测得轨道精度比改造前提高了一个数量级,有效地修正了轨道高差引起的指向精度偏差。

|
| 图 1 南山26 m射电望远镜 Fig. 1 NSRT 26m telescope |

|
| 图 2 南山26 m射电望远镜焊接轨道 Fig. 2 Welding joint of NSRT |
文[4]采用数字水准仪测量了改造前的轨道高差。研究发现,轨道接缝处是影响天线指向精度的主要因素,指向误差通过4个固定方位拟合得到,存在较大的拟合误差。文[5]在文[4]的基础上在改造后的天线二次平台上测量天线的轨道高差,对天线指向进行修正,同样也存在较大的拟合误差。密云50 m射电望远镜考虑轨道不平度[6],利用有限元仿真得到天线方位轴倾斜误差,得到非线性指向的修正模型,使用有限元仿真会使计算结果存在一定的偏差。上海天马65 m射电望远镜采用了单台倾角仪和水准仪[2]测量轨道高差,研究轨道沉降对天线指向的影响。意大利撒丁岛64 m[7]和美国深空探测网(Deep Space Network, DSN)34 m[8]等使用倾角仪测量大口径射电望远镜的轨道高差,计算出天线的指向偏差。本文建立轨道高差引起天线指向偏差的模型,选取射电源通过“十字扫描”法进行实测得到指向偏差,对比实测值与轨道高差引起的指向偏差用以修正指向。
1 轨道高差测量 1.1 轨道高差测量方案26 m射电望远镜轨道改造为11段弧形钢轨整体焊接式轨道,轨道直径15 m、宽210 mm。整个改造过程中,在灌浆浇筑前、轨道底部悬空部分灌浆浇筑后和轨道上加载天线载荷后3个不同施工期对天线轨道精度进行了测量,前2期测量结果主要说明轨道灌浆的质量达到了天线安装过程的精度要求,第3期是轨道加载荷后正常运行一段时间测量,结果作为天线改造完成后的精度指标。
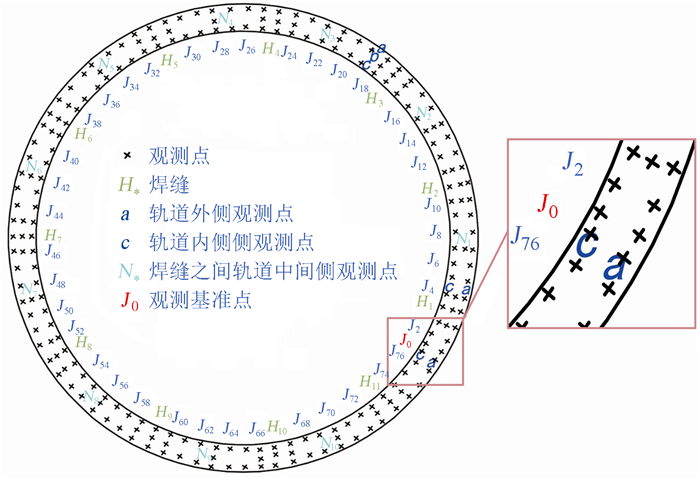
由于白天温差大对数据的准确性产生较大影响,因此测量时间调整到夜间23:30以后,此时环境温度较为均匀,测得的数据比较准确。使用徕卡高精度水准仪和高度尺测量,在轨道上布设220个观测点,轨道内外圈各布88个点,轨道中圈布44个点,具体布设如图 3。
|
| 图 3 南山26 m射电望远镜轨道观测点和焊缝分布 Fig. 3 NSRT 26m track observation point and weld distribution |
以J0为观测基准点,逆时针顺序编号,标记观测点77个(单圈),共内外2圈。在与焊缝相邻的校正点处中间位置加测2个点,焊缝以H1逆时针顺序编号,标记观测点11个(单圈),共内中外3圈,在焊缝与焊缝之间的轨道中间位置,以N1逆时针顺序编号,标记观测点11个。为了区分内外轨道,以字母a表示外侧轨道,b表示中间轨道,c表示内侧轨道,共标记观测点220个。
1.2 轨道高差测量结果 1.2.1 轨道改造3期的高差测量和数据分析26 m射电望远镜的轨道不平度要求为0.45 mm(峰峰值),在轨道焊接后、灌浆后以及天线落到轨道上运转一段时间后,对轨道不平度进行了3次测量。对轨道施工中的每个关键阶段进行监测可以及时修正装调误差,为满足轨道精度要求起到重要的作用。
(1) 第1期轨道在灌浆浇筑前的测量高差
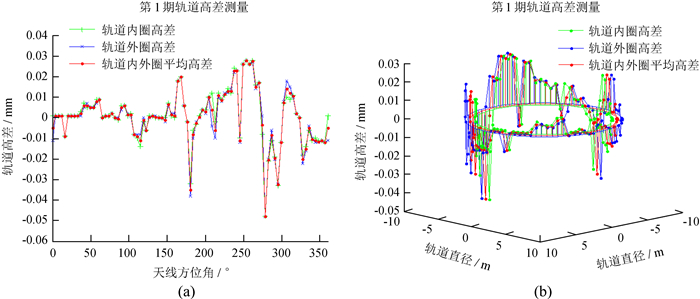
第1期轨道高差的测量结果如图 4。轨道在没有灌浆之前,轨道的内外圈的高差峰峰值都是0.076 mm,并且内外圈的高差基本一致。焊缝处的高差值跟其他标记点处高差值比较接近,说明轨道的焊接质量较好。计算可知,轨道内外圈高差的均方根(Root Mean Square, RMS)值分别为0.012 8 mm、0.013 0 mm。
|
| 图 4 南山26 m射电望远镜轨道高差分布 Fig. 4 NSRT 26m track unevenness distribution |
(2)第2期轨道底部灌浆浇筑后测量高差
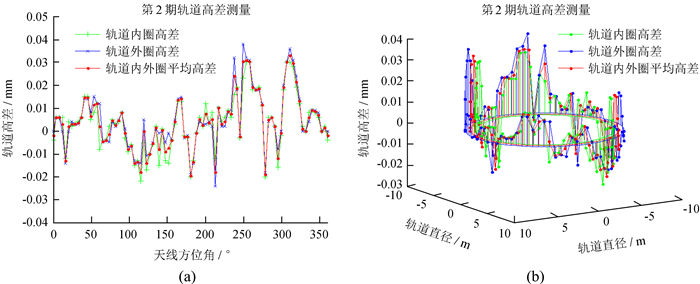
轨道底部悬空部分灌浆浇筑后轨道的精度会发生变化,本次测量检测灌浆工艺,保证灌浆后轨道高差在允许范围内。第2期测量结果如图 5,轨道内外圈高差峰峰值分别为0.052 mm、0.062 mm,均小于没有灌浆的轨道高差峰峰值0.076 mm。计算得到内外圈轨道高差的均方根值分别为0.012 3 mm、0.0132 mm。分析可知,灌浆后轨道内圈的高差略好于灌浆前,外圈的高差与灌浆前基本一致。综上表明,所采用的灌浆工艺是成功的。
|
| 图 5 南山26 m射电望远镜轨道高差分布 Fig. 5 NSRT 26m track unevenness distribution |
(3) 第3期轨道加载天线载荷后测量
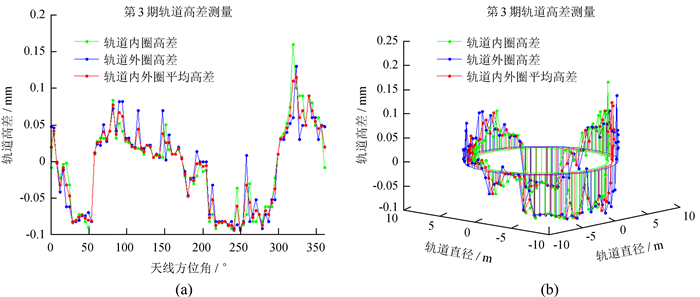
在轨道浇筑完成后,天线坐落在轨道上,正常运行一段时间,对轨道高差进行了测量。第3期测量结果如图 6,图中轨道内外圈高差的峰峰值分别为0.254 mm、0.222 mm。计算得到轨道内外圈高差的均方根值分别为0.057 8 mm、0.056 2 mm,可以看出这次轨道内外圈高差的均方根值均大于前2期的均方根值。说明轨道承载后精度受到一定影响,但仍满足设计需求。另外,轨道改造之前拼接轨道峰峰值为1.200 mm,采用整体焊接轨道技术后轨道精度提高了近一个数量级。
|
| 图 6 南山26 m射电望远镜轨道高差分布 Fig. 6 NSRT 26m track unevenness distribution |
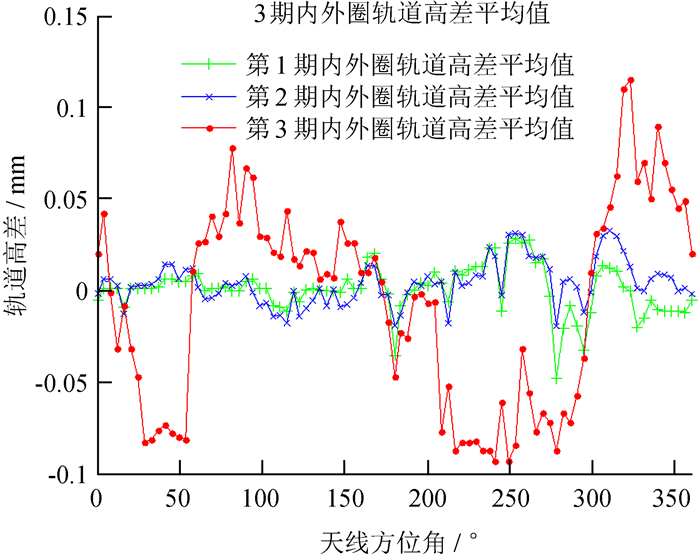
图 7显示了3期轨道内外圈高差平均值的分布,可以清楚地看到轨道浇筑前、浇筑后和加载荷后高差分布的变化。前2次测量轨道没有载荷,变形较小,在0°~270°;第2期的高差变化比第1期高差变化大,灌浆对这部分轨道影响明显,在270°~360°;第2期轨道高差变化比第1期轨道高差变化小,表明灌浆后一部分轨道高差被优化;第3期轨道高差变化最大,说明承载后对轨道精度有一定影响。
|
| 图 7 内外圈轨道平均高差分布 Fig. 7 Average unevenness distribution in inner and outer track |
测得的轨道高差数据是离散的点,为充分地分析轨道高差与指向偏差之间的关系,需要完全显示轨道高差的连续变化,对第3期轨道高差进行拟合。
轨道高差包含了正弦分量,对内外圈平均高差进行傅里叶和正弦函数八阶拟合,拟合函数的系数通过非线性最小二乘拟合得到,正弦函数拟合的均方根误差(Root Mean Square Error, RMSE)为0.016 9,傅里叶函数拟合的均方根误差为0.017 2。由图 8可以看出,正弦函数拟合不仅从大尺度(0°~360°)拟合出了轨道高差变化,也从小尺度拟合出了轨道高差的波动变化,所以正弦函数拟合更接近真实测量值,这样可以通过拟合函数求出未测量点的高差值。

|
| 图 8 南山26 m射电望远镜轨道高差拟合 Fig. 8 NSRT 26m track unevenness fitting |
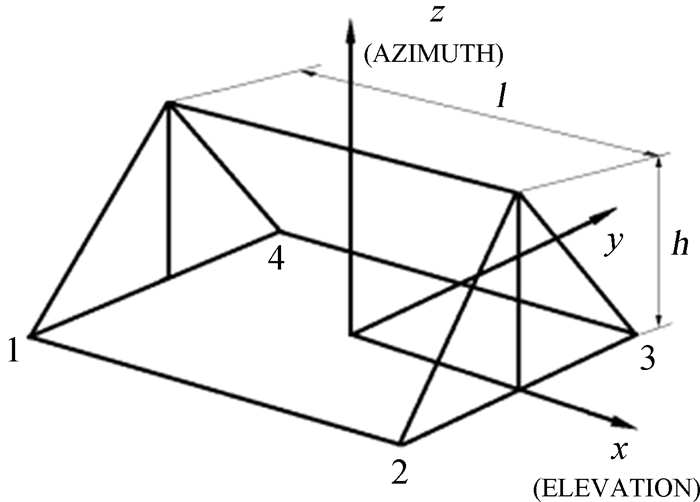
天线座架跟轨道面是4个轮子的点接触[9],通过轨道4点高差可以计算出座架绕三坐标轴的转角,如图 9:其中,正北(坐标y轴的正向)是方位0°,逆时针旋转一圈是方位0°~360°。在三维坐标系中,1、2、3、4点逆时针编号,分别代表座架与轨道接触的4点。l表示1、2两点或4、3两点之间的距离,h表示座架高度,r表示轨道半径,求解座架绕x,y和z轴的转角都采用右手定则。
|
| 图 9 南山26 m射电望远镜座架坐标系 Fig. 9 NSRT 26m coordinate of the alidade structure |
计算座架绕x轴的转角ax,h1,h2,h3,h4分别表示1、2、3、4这4点的高差,图 9中4、1两点和3、2两点共同作用引起座架绕x轴转动,求得4、1和3、2两组转角,取它们的平均值,则转角ax的计算公式为
| $ {a_{\rm{x}}} \approx \frac{1}{2}\left( {\frac{{{h_4} - {h_1}}}{{2r\cos \frac{{\rm{ \mathsf{ π} }}}{4}}} + \frac{{{h_3} - {h_2}}}{{2r\cos \frac{{\rm{ \mathsf{ π} }}}{4}}}} \right) = \frac{1}{{2\sqrt 2 r}}\left[ {\begin{array}{*{20}{c}} { - 1}&{ - 1}&1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}}\\ {{h_3}}\\ {{h_4}} \end{array}} \right]. $ | (1) |
计算座架绕y轴的转角ay,图 9中4、3两点和1、2两点共同作用引起座架绕y轴转动,求得4、3和1、2两组转角,取它们的平均值,则转角ay的计算公式为
| $ {a_{\rm{y}}} \approx \frac{1}{2}\left( {\frac{{{h_4} - {h_3}}}{{2r\cos \frac{{\rm{ \mathsf{ π} }}}{4}}} + \frac{{{h_1} - {h_2}}}{{2r\cos \frac{{\rm{ \mathsf{ π} }}}{4}}}} \right) = \frac{1}{{2\sqrt 2 r}}\left[ {\begin{array}{*{20}{c}} 1&{ - 1}&{ - 1}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}}\\ {{h_3}}\\ {{h_4}} \end{array}} \right]. $ | (2) |
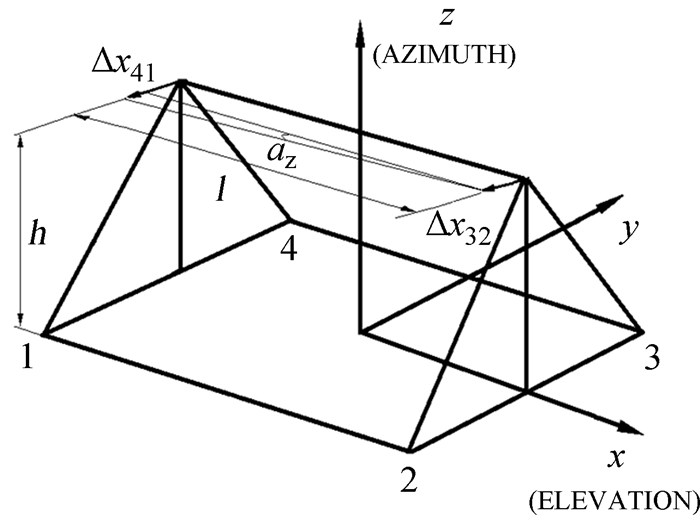
计算绕z轴的旋转角az,由于绕z轴的旋转受到座架绕x轴的影响,图 10中Δx41是由4、1两点的高差引起的,Δx32是由3、2两点的高差引起的,Δx41,Δx32使座架绕z轴产生旋转角az,则转角az的计算公式为
| $ {a_{\rm{z}}} \approx \frac{{\Delta {x_{41}} - \Delta {x_{32}}}}{l}, $ | (3) |
|
| 图 10 南山26 m射电望远镜座架绕z轴转角 Fig. 10 The angle of the NSRT 26m alidade structure of the z-rotation |
其中,
| $ \Delta {x_{41}} \approx h\left( {\frac{{{h_4} - {h_1}}}{{2r\cos \frac{{\rm{ \mathsf{ π} }}}{4}}}} \right) = h\left( {\frac{{{h_4} - {h_1}}}{{\sqrt 2 r}}} \right), $ | (4) |
| $ \Delta {x_{32}} \approx h\left( {\frac{{{h_3} - {h_2}}}{{2r\cos \frac{{\rm{ \mathsf{ π} }}}{4}}}} \right) = h\left( {\frac{{{h_3} - {h_2}}}{{\sqrt 2 r}}} \right), $ | (5) |
| $ l = 2r\cos \frac{{\rm{ \mathsf{ π} }}}{4} = \sqrt 2 r, $ | (6) |
那么
| $ {a_{\rm{z}}} \approx \frac{{h\left( {\frac{{{h_4} - {h_1}}}{{\sqrt 2 r}}} \right) - h\left( {\frac{{{h_3} - {h_2}}}{{\sqrt 2 r}}} \right)}}{{\sqrt 2 r}} = \frac{h}{{2{r^2}}}\left[ {\begin{array}{*{20}{c}} { - 1}&1&{ - 1}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}}\\ {{h_3}}\\ {{h_4}} \end{array}} \right]. $ | (7) |
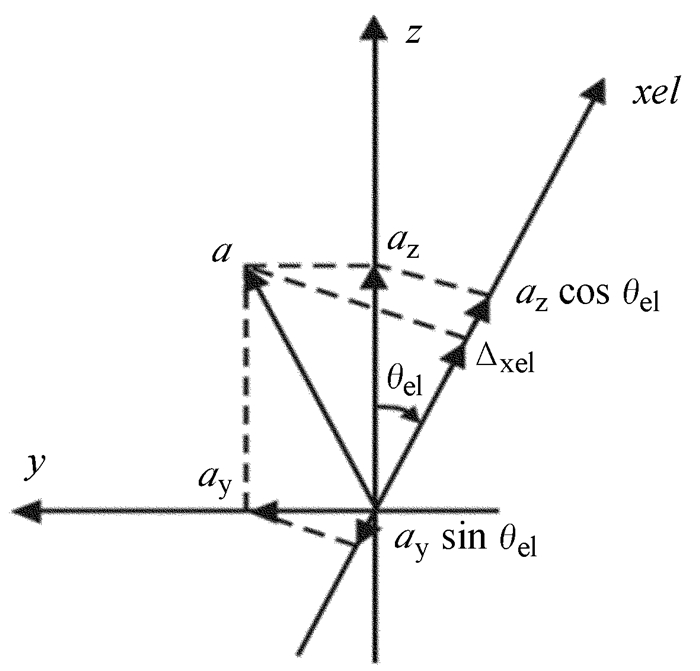
由于x轴跟俯仰轴平行,因此,天线俯仰方向指向偏差ael=ax;方位轴方向的指向偏差受到转角ax,ay和az的综合影响,所以方位方向的指向偏差aaz[10]计算较复杂。如图 11,轴xel垂直于指向平面,θel是方位角,aaz的计算公式为
| $ {a_{{\rm{az}}}} = \frac{{{\Delta _{{\rm{xel}}}}}}{{\cos {\theta _{{\rm{el}}}}}}, $ | (8) |
|
| 图 11 方位指向误差计算 Fig. 11 Calculation of azimuth pointing error |
其中,
| $ {\Delta _{{\rm{xel}}}} = {a_{\rm{z}}}\cos {\theta _{{\rm{el}}}} - {a_{\rm{y}}}\sin {\theta _{{\rm{el}}}}, $ | (9) |
那么
| $ {a_{{\rm{az}}}} = {a_{\rm{z}}} - {a_{\rm{y}}}\tan {\theta _{{\rm{el}}}}. $ | (10) |
由于计算结果是弧度值,需要乘上系数k=180×3 600π,得到角秒(″)。综上可得,轨道高差引起天线方位、俯仰指向偏差的计算公式为
| $ \left[ {\begin{array}{*{20}{c}} {{a_{{\rm{az}}}}}\\ {{a_{{\rm{el}}}}} \end{array}} \right] = k\left[ {\begin{array}{*{20}{c}} {{a_{\rm{z}}} - {a_{\rm{y}}}\tan {\theta _{{\rm{el}}}}}\\ {{a_{\rm{x}}}} \end{array}} \right] = k\left[ {\begin{array}{*{20}{c}} {\frac{h}{{2{r^2}}}}&{ - \frac{{\tan {\theta _{{\rm{el}}}}}}{{2\sqrt 2 r}}}&0\\ 0&0&{\frac{1}{{2\sqrt 2 r}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - 1}&1&{ - 1}&1\\ 1&{ - 1}&{ - 1}&1\\ { - 1}&{ - 1}&1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}}\\ {{h_3}}\\ {{h_4}} \end{array}} \right], $ | (11) |
天线的指向偏差δ的计算公式为
| $ \delta = \sqrt {{a_{{\rm{az}}}}^2 + {a_{{\rm{el}}}}^2} . $ | (12) |
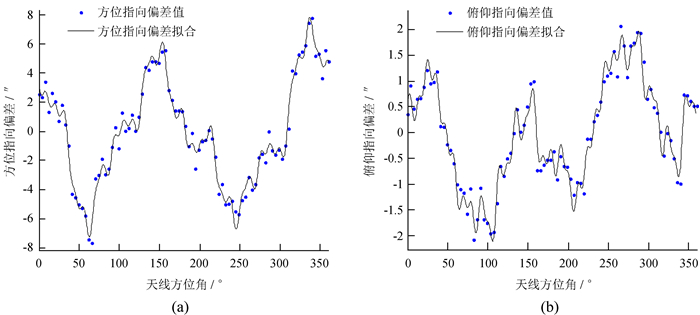
对(11)式,取俯仰角为45°时,代入轨道高差,计算方位、俯仰指向偏差值。如图 12,偏差值中含有周期成分。对计算结果进行了正弦函数拟合,得到方位指向偏差值-7.761 4″~7.654 4″,俯仰指向偏差值-2.080 8″~2.080 8″。可以看出方位指向偏差值较大,俯仰偏差值相对较小,这是由于方位偏差的计算计入了座架绕x, y轴的转角,所以方位指向偏差值比较大。
|
| 图 12 南山26 m射电望远镜指向。(a)方位指向偏差,(b)俯仰指向偏差 Fig. 12 NSRT 26m pointing error. (a) Azimuth pointing error, (b) Elevation pointing error |
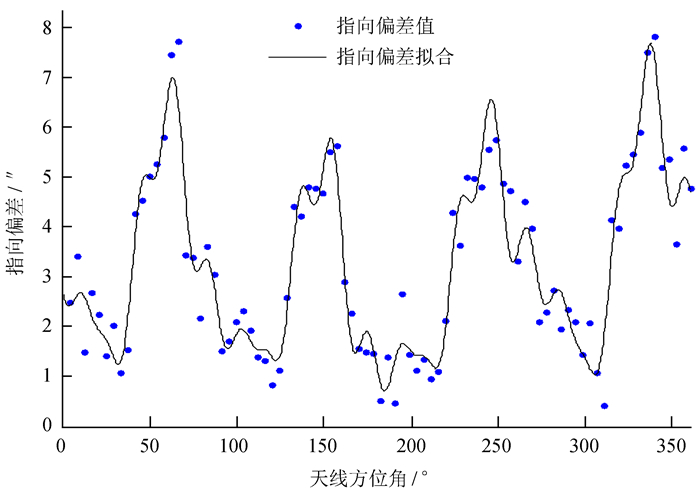
图 13中天线的指向偏差由(12)式计算得到,指向偏差值0.432 4″~7.825 1″,指向偏差是由轨道上4点高差计算得到,所以轮子每转过90°,4点高差就会重复出现,但是计算的方向不一样,指向偏差呈现一定的周期性。把图 13中的指向偏差和图 6(a)中的轨道高差进行对比,可以得出,高差大的地方不是天线指向偏差最大的地方,因为指向偏差是由天线的每个位置对应轨道上4点的高差共同作用的结果。
|
| 图 13 南山26 m射电望远镜指向偏差 Fig. 13 NSRT 26m pointing error |
本次测量时间为白天,使用“十字扫描”对多颗标准射电源进行扫描测量,一次方位或俯仰扫描用时60 s,每秒采集功率读数2次,测得高精度的功率读数,同时控制天线扫描并实时读取天线位置信息,每次方位或俯仰扫描记录120个数据。使用高斯拟合这些标准射电源的实际指向偏差,并与前述模型计算的指向偏差进行对比用以修正指向偏差。
因为“十字扫描”是对方位、俯仰分别进行扫描,在一次方位和俯仰扫描的过程中标准源位置时刻在变化,所以当方位扫描结束,可以拟合与方位扫描对应的方位、俯仰坐标,与接下来的俯仰扫描时的方位、俯仰坐标位置是不一样的。俯仰扫描结束,可拟合俯仰扫描对应的方位、俯仰坐标。使用拟合得到的方位、俯仰坐标值,通过前述模型可以算出此位置上由轨道高差引起的方位、俯仰指向偏差,实测指向偏差值和轨道高差计算得到的指向偏差值的结果如表 1和表 2。
| 源名 | 方位/° | 俯仰/° | 实测方位偏差/″ | 高差引起的方位偏差/″ |
| 3C274 | 101.597 5 | 29.156 5 | -21.755 5 | -0.243 4 |
| 3C286 | 75.987 8 | 30.604 1 | -17.658 6 | -3.344 1 |
| 3C295 | 49.586 1 | 36.176 1 | -8.078 5 | -5.204 1 |
| 4C39.25 | 89.366 6 | 64.895 1 | -9.167 4 | -0.530 7 |
| 3C144 | 246.451 3 | 53.185 2 | -8.465 2 | -6.499 5 |
| 3C147 | 310.833 1 | 79.098 3 | -7.763 3 | -2.702 1 |
| 源名 | 方位/° | 俯仰/° | 实测俯仰偏差/″ | 高差引起的俯仰偏差/″ |
| 3C274 | 101.815 7 | 29.355 5 | -27.792 1 | -1.793 2 |
| 3C286 | 76.152 4 | 30.802 4 | -18.046 8 | -1.426 1 |
| 3C295 | 49.682 5 | 36.331 9 | -9.144 2 | -0.136 1 |
| 4C39.25 | 89.553 8 | 65.100 8 | -7.344 1 | -1.419 1 |
| 3C144 | 246.754 6 | 53.000 2 | -9.684 1 | 1.391 1 |
| 3C147 | 310.345 6 | 78.943 2 | -11.397 6 | 0.570 5 |
表 1、表 2中实测的标准射电源,通过高斯拟合得到它们方位和俯仰的位置,再拟合得到它们在该方位和俯仰位置时的真实指向偏差值,把拟合的方位和俯仰坐标代入前述轨道高差,计算天线指向偏差的模型,算出该方位和俯仰位置时轨道高差引起的指向偏差值。使用轨道高差计算的方位、俯仰指向偏差值,修正实测的方位、俯仰指向偏差,结果表明,天线的指向精度得到了提高。
4 结论本文介绍了采用高精度焊接轨道技术后26 m射电望远镜轨道峰峰值由改造前的1.200 mm提高到0.254 mm。为了修正因轨道高差造成的指向偏差,建立了轨道高差计算天线指向偏差模型。基于“十字扫描”法测量了26 m射电望远镜的指向精度,通过比较发现,修正轨道高差引起的指向偏差后,天线整体指向精度得到改善。
天线的指向偏差由结构、控制和环境等因素综合作用产生,轨道高差引起的天线指向偏差只是结构因素中的一小部分,所以还得综合考虑各种因素,如温度、风等引起的误差,南山26 m射电望远镜已经做了一些有关温度对天线座架影响的工作[11],下一步将构建基于温度可控、湿度可监测的双倾角仪轴系偏差测量系统,实时测量天线座架结构全天候变形情况,并构建模型修正指向误差。
| [1] | SYMMES A, ANDERSON R, EGAN D. Improving the service life of the 100-meter green bank telescope azimuth track[C]//Proceedings of SPIE. 2008. http://adsabs.harvard.edu/abs/2008SPIE.7012E..38S |
| [2] | 付丽, 凌权宝, 赵融冰, 等. TM 65m天线基础和轨道沉降及对天线指向的影响[J]. 红外与激光工程, 2016, 45(11): 190–196 |
| [3] | 王娜. 新疆奇台110米射电望远镜[J]. 中国科学:物理学力学天文学, 2014, 44(8): 783–794 |
| [4] | 李永江, 艾力·玉苏甫, 张正禄, 等. 天线轨道变形精密测量与指向偏差模型研究[J]. 武汉大学学报(信息科学版), 2013, 38(2): 176–180 |
| [5] | 刘璇, 艾力·玉苏甫, 项斌斌, 等. 轨道不平度对天线指向的影响分析与修正[J]. 天文学报, 2017, 58(4): 47–57 |
| [6] | 姜正阳, 孔德庆, 张洪波, 等. 考虑轨道不平度的射电望远镜指向修正方法[J]. 天文研究与技术, 2015, 12(4): 417–423 DOI: 10.3969/j.issn.1672-7673.2015.04.005 |
| [7] | TONINO P, FRANCO B, SERGIO P, et al. The SRT inclinometer for monitoring the rail and the thermal gradient effects on the alidade structure[C]//Proceedings of SPIE. 2014, 9145: 72-78. |
| [8] | GAWRONSKI W. Modeling and control of antennas and telescopes[M]. New York: Springer, 2008: 211-222. |
| [9] | 吴江. 110米高精度全可动反射面天线轨道不平度及其对指向精度的影响[D].西安: 西安电子科技大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10701-1016248175.htm |
| [10] | GAWRONSKI W, BAHER F, QUINTERO O. Azimuth-track-level compensation to reduce blind-pointing errors of the beam-waveguide antennas[R]. The Telecommunications and Mission Operations Progress Report, 1999, 139: 1-18. http://adsabs.harvard.edu/abs/1999tmopr.139d...1g |
| [11] | 王惠, 宁云炜, 闫浩. 26米天线座架温度分布规律及变形影响分析[J]. 天文研究与技术, 2018, 15(2): 208–215 |


