2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
抚仙湖1 m新真空太阳望远镜(New Vacuum Solar Telescope, NVST)是国内口径最大的地基太阳望远镜[1],已经获得了大量长时间、亚角秒的太阳高分辨成像观测资料[2]。目前,成像观测系统包括TiO和G-band两个用于光球观测的宽带通道及Hα,Ca Ⅱ和He Ⅰ三个用于色球观测的窄带通道。众所周知,太阳色球层中有许多重要的活动现象,如日珥、谱斑和耀斑等,但太阳色球在整个可见光波段的辐射能量只有光球的万分之一,色球结构难以探测[3],因而通常使用窄带滤光设备,诸如珐珀滤光器[4]或里奥滤光器[5],以获得某个波长点的单色像。但是,单一波长的单色像包含的物理信息有限,无法直接区分辐射和多普勒速度引起的观测强度的变化,因此单色像观测通常需要在线心-线翼间的多个波长点上进行,这有助于太阳结构的动力学特征的研究[6]。目前1 m太阳望远镜的3个窄带成像通道均使用由南京天文光学技术研究所研制的里奥滤光器,其中心波长可调,以实现多波长点依次观测的要求。表 1给出3个窄带通道的中心波长、中心波长变化范围以及透过带带宽。
| 通道 | 中心波长/nm | 透过带宽/nm |
| Hα | 656.28±0.4 | 0.025 |
| Ca Ⅱ | 393.3±1 | 0.025 |
| He Ⅰ | 1 083±0.4 | 0.05 |
目前1 m太阳望远镜主要在Hα通道进行太阳色球常规观测,为了确保滤光器稳定的工作状态,工作人员需要定期检测滤光器的性能,特别是检查滤光器中心波长的变化以及波长扫描轮廓的对称性,操作方法和细节见文[6]。但文[6]对整个观测视场的光强值进行空间积分获取某一波长点的强度,忽略了视场内强度分布的问题。图 1展示了偏带值为-0.06 nm、-0.02 nm、0 nm、+0.02 nm、+0.06 nm一系列太阳宁静区的Hα波段观测结果。图中存在除太阳结构以外的大尺度亮度不均匀现象,最明显的是左上方与右上方的明暗情况,其亮度随偏带值变化而变化。

|
| 图 1 Ha通道各个偏带太阳像示例 Figure 1 Examples of the observation data from different working wavelength |
视场内亮度不均匀现象的成因有很多,比如杂散光、光路渐晕、探测器的不均匀性等。但是图 1表现出亮度不均匀对波长敏感,因此更倾向于滤光器的视场效应。所谓滤光器的视场效应是指当入射光并非严格垂直入射滤光器时,滤光器透过带中心波长相较于垂直入射时发生偏移,该偏移量与入射角大小有关[5]。
1 数据采集及分析 1.1 采集方式首先,波长扫描方式如下:扫描偏带范围为-0.1~+ 0.1 nm,扫描步长(单步波长间隔)0.01 nm,每步采集10~20帧数据。一次完整的波长扫描共采集包含1个线心和20个不同偏带点。
其次,注意观测目标的选择与平滑。由图 1可见,视场内除了大尺度的亮度不均匀外还有小尺度的太阳色球结构,为避免太阳结构对实验结果造成影响,在日面中心附近不同区域的宁静区进行数据采集并将多组结果叠加。
1.2 数据初步处理为了研究视场内亮度空间分布不均现象,将视场分为3×3个子块(分块情况如图 1(c)红虚线框所示),分别考察这9个子块中扫描轮廓的特性。考虑到轮廓的清晰展示,在图 2中只显示了中心区域与四角区域的扫描轮廓,为了剔除由光路渐晕、杂散光等因素产生的亮度变化的影响(如图 1左上角亮度在各个偏带点均偏暗,这里渐晕占主要因素),所有轮廓根据中心区域在线翼-0.1 nm的强度值进行归一化发现:(1)各个区块扫描轮廓并不重合,之间存在相对频率漂移;(2)相对于中心区域的轮廓,四角区域的轮廓全部发生了蓝移。

|
| 图 2 中心区域与四角区域波长扫描轮廓对比 Figure 2 Comparison between the profile from central area and four corner areas |
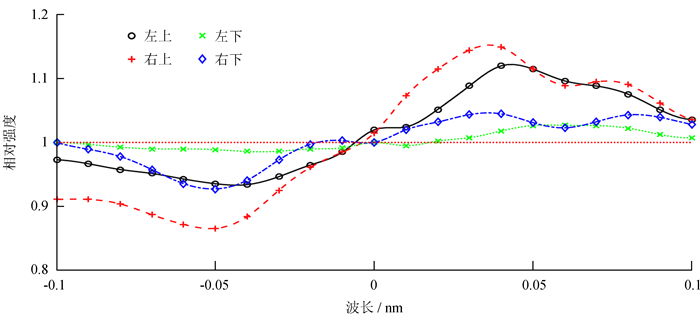
为了更直观地展现频漂相对大小,进一步分析了四角区域与中心区域的相对光强,即分别将四角区域强度与中心区域做比值,如图 3。从图 3可以看出:(1)4条比值曲线均呈现不同程度的左(蓝移)低右(红移)高的形态。对于呈吸收状的Hα谱线轮廓而言,这充分说明了四角区域的轮廓相对蓝移的结论,体现在观测数据上就是该区域蓝移观测时强度相对较弱,而红移观测时强度相对较强。(2)比值曲线最远离1的位置出现在右上角(图 1也可以明显看到该区域由暗变亮的过程,对于比值曲线同样远离1的左上角,虽然图 1中该区域均较暗,但仔细观察仍可发现其相对亮度随波长的变化),比值曲线最接近1的位置出现在左下角。也就是说,四角区域相对中心频漂量值大小不一,并不呈中心对称分布。
|
| 图 3 四角区域相对中心区域的强度比值 Figure 3 Intensity ratio of four corner areas to central area |
为了研究视场频漂的形成机制,需要定量计算各个区域相对于中心区域的频漂量。利用重心法计算每个子块的扫描轮廓的中心波长,所求中心波长的差异即可表征相对频漂量。这里说明两点:(1)虽然轮廓出现频漂,但基本形状不变(没有受到太阳动力学结构的影响),这样即便是Hα轮廓存在系统的不对称性,也只影响频漂的绝对大小,不影响“相对”频漂的计算结果;(2)只利用±0.05 nm范围内的轮廓进行重心法计算,尽量减少轮廓系统性不对称对结果的影响。在3×3子块的情况下,各区块相对于中心的频漂量如表 2。
| 行号 | 列号 | ||
| 1 | 2 | 3 | |
| 1 | -0.006 37 | -0.003 86 | -0.010 10 |
| 2 | -0.002 03 | 0 | -0.003 65 |
| 3 | -0.001 29 | -0.000 54 | -0.003 45 |
可以发现:边缘区域相对于中心区域均呈现一致性的蓝移;各个区域蓝移的程度不相同,且最大值为-0.01 nm,出现在右上角,与图 3结果符合很好,这在一定程度上说明了重心法的正确性。
上述3×3子块描述频漂空间分布显得比较粗糙,于是将子块分割得更为细腻。图 4是将视场分为9×9、15×15、25×25子块后频率相对漂移的情况。在3种情况的计算中,均以位于几何中心子块的中心波长作为参考。

|
| 图 4 观测图像采取不同分割程度时频漂量计算结果。上方为各个区域的频漂大小,下方为等值线 Figure 4 Frequency drifts of different segmentationlevels |
从图 4可以看出,频漂的空间分布几乎呈圆形,对称中心位于中心偏左下的区域,并非视场中心,且这种空间分布趋势与区域分割的程度没有关系,但提高分割程度的确可以体现太阳色球结构对结果的影响,故下文仅取视场分为9×9子块的情况进行讨论。
针对以上结果认为,对称中心未出现在视场中心是光路非理想性所致,可以通过调节探测器的空间位置改善。
3 视场频漂的成因分析实际使用的里奥滤光器均做宽视场处理,其中一个宽视场单元如图 5[7],图中P为偏振片,两晶片C的光轴互相垂直,中间内插消色差半波片,其光轴与二晶片的光轴均成45°角。若不考虑晶体定轴误差等影响,理想的宽视场滤光器视场效应定量关系如下[5]:
| $ \frac{\delta \lambda }{\lambda }=\frac{1}{4n_{\text{o}}^{2}}\frac{{{n}_{\text{e}}}-{{n}_{\text{o}}}}{{{n}_{\text{e}}}}{{\sin }^{2}}\theta , $ |

|
| 图 5 里奥滤光器宽视场单元 Figure 5 Wide-field birefringent element |
其中,θ为光线至滤光器的入射角;λ为透过带中心波长;δλ为中心波长偏移量;no和ne分别是晶体的o光及e光主折射率。显然,只要光线偏离垂直入射,δλ就不为0,就会发生频率漂移。以上公式只是近似公式,实际里奥滤光器的透过率还随着入射光线方位角的变化而变化。文[8]指出,相比于光线的倾斜入射,频漂随光线方位角改变所产生的变化量要小两个量级以上,其效应可以忽略。当然,如果构成里奥滤光器宽视场单元的晶体光轴有定轴误差,这也导致频漂的产生,并进一步突显透过率与入射光线方位角之间的关系[7],在此认为定轴误差很小,不对透过率造成明显影响。
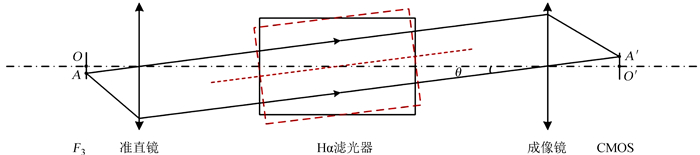
在实际观测系统中,Hα通道滤光器位于平行光路中(准直镜之后,成像镜之前),如图 6。光路的精确装调可以较好地保证视场中心的光线(即o-o′连线)平行于系统的光轴,并垂直入射至滤光器。但来自边缘视场的光线,例如A点发出的光线,在经过准直镜后形成与光轴夹角为θ的平行光,即入射滤光器的角度不为0,因此该光线经过滤光器时透过带的中心波长发生δλ的偏移。由于Hα里奥滤光器使用的晶体为冰洲石(ne<no),δλ为正值,也就是说不管θ为正或负,透过率曲线必然发生红移。当透过率曲线作用在Hα这条吸收轮廓上时,表现出来的是吸收轮廓的蓝移,因此边缘区域的扫描轮廓曲线相对中心区域总是蓝移。
|
| 图 6 Ha通道光路示意图 Figure 6 Schematic diagram of Ha channel |
在此基础上,零频率点不在视场中心的现象可能由两种原因导致:(1)系统光轴并未穿过探测器中心位置。如果探测器沿垂直于光轴方向移动,那么必然导致零频漂位置偏离探测器中心;(2)探测器位置正确,但滤光器光轴与系统光轴相对倾斜(如图 6中的红虚线框),此时不是视场中心点(O点),而是由视场内另一点(例如A点)发出的光线平行于滤光器的光轴。对该光线来说,透过率不会改变,因而零频漂点出现在偏离视场中心的其它位置(A′点),而且视场的最大频漂量会变大,如图 4右上角的情况。
接下来讨论对于Hα通道近2′的视场,观测到的频漂量是否符合上述频漂量值与滤光器入射角的定量关系。首先对9×9子块得到的频漂数据进行二维曲面拟合,找到该拟合曲面的对称中心,然后分别计算81(9×9)个子块距离该中心的空间距离(空间距离=像素尺寸×像素数),并转化为光线的入射角(入射角≈

|
| 图 7 实测频漂量及其拟合曲线与理论曲线 Figure 7 Measured results of frequency drift, fitting curve and theoretical curve |
从图 7可以看到:(1)实测值(星点)与理论值(黑实线)的基本趋势一致,可进一步确定观测视场中的亮度不均现象的确反应了滤光器的视场效应;(2)实测频漂量要比理论预测稍大。对此可以理解为,理论值的计算是基于理想光路状态,而实际还存在非理想因素,包括滤光器的非理想性、光学系统中光学元件未严格共轴以及探测器靶面未严格位于成像镜焦平面等;(3)由于太阳结构的存在,实测数据结果具有一定的离散性,但多组观测数据给出一致的拟合曲线(红虚线);(4)实测值与理论值的差异随着视场角的增大而增大。
4 研究视场频漂的意义视场内频漂的程度以及空间分布的特征可以较好地反应光路的工作状态,举例来说,1 m太阳望远镜的Hα通道曾在2017年3月前后进行过一次光路调整,对比光路调整之后频漂的程度和空间分布特点,如图 8。图 8(a)是光路调整之前(2016年12月,红虚线)和光路调整之后(2017年6月,蓝点划线)视场内的实际频漂与理论预测(黑线)的对比,后者更接近理论预测情况。图 8(c)是光路调整之后,由于更换探测器,缩小了观测视场,视场相对大小如图 8(b)红虚线框,而且在较小的视场内,频漂量最大值减小且仅出现在视场的左下边缘,由原来的0.01 nm变为目前的0.005 nm,此外空间分布较为均匀。

|
| 图 8 (a) 理论曲线与两次实测曲线对比; (b) 2016年12月结果; (c) 2017年6月结果 Figure 8 (a) Comparison of thetheoretical curve and themeasured results in two different times; (b) The result in Oct. 2016; (c) The result in Jun. 2017 |
从视场频漂的研究可知,Hα通道乃至其他里奥滤光器系统均存在视场频漂问题。因此1 m太阳望远镜系统扫描轮廓以及波长定标工作[6]可以将原先的全视场平均进一步修改为视场分块讨论,选取最优区块作为参考位置,从而降低平均效应并给出更为细致精确的结果。另外,在1 m太阳望远镜现行的平场处理[9]过程中并没有区分光强空间分布不均匀是由光路渐晕、杂散光所引起还是滤光器视场效应所引起,而有了视场频漂数据便可以在以后的平场处理中给出参考。
5 总结与讨论综上,对Hα通道波长扫描数据分析可见,观测图像视场内亮度不均匀现象的直接原因是视场中心区域与其他区域有相对频漂,产生频漂的根本原因是滤光器的视场效应。通过近期望远镜以及成像系统光路的进一步调整,目前在2.2′的视场内,频漂量的最大值约为0.005 nm,小于滤光器的透过带带宽。频漂最大值仅出现在视场左下边缘,因此对观测数据,特别是多普勒速度的判断,影响不明显。
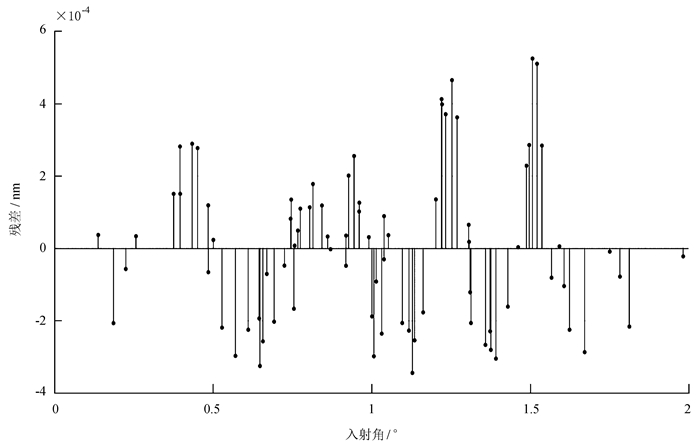
进一步分析发现,实测频漂值与理论频漂值的残差与入射角的关系呈现图 9的样式,其中结果已经过均值滤波。
|
| 图 9 均值滤波后实测结果与其拟合曲线残差 Figure 9 Residual error of frequency drift after mean filtering |
图 9可以看出残差呈现一个有规律的起伏,且起伏周期随入射角的增大而减小。由于现阶段数据量较少,连续采集大量数据存在时间成本过高以及太阳光强变化等问题,故还无法对其成因作出判断。当然,日后可以针对这一问题考虑对频漂对称中心位置计算准确程度以及频漂量分布是否与方位角有关等方面进行详细探讨,从而给出合理的解释。
| [1] | Liu Z, Xu J. 1-meter near-infrared solar telescope[C]//Astronomical Society of India Conference Series. 2011. http://adsabs.harvard.edu/cgi-bin/nph-data_query?bibcode=2011ASInC...2....9L&db_key=AST&link_type=ABSTRACT |
| [2] | Wang R, Xu Z, Jin Z Y, et al. The first observation and data reduction of the multi-wavelength spectrometer on the New Vacuum Solar Telescope[J]. Research in Astronomy and Astrophysics, 2013, 13(10): 1240–1254. DOI: 10.1088/1674-4527/13/10/012 |
| [3] | 林元章. 太阳物理导论[M]. 北京: 科学出版社, 2001. |
| [4] | Perot A, Fabry C. On the application of interference phenomena to the solution of various problems of spectroscopy and metrology[J]. Astrophysical Journal, 1899, 9: 87–115. DOI: 10.1086/140557 |
| [5] | Title A M, Rosenberg W J. Improvements in birefringent filters. 5:field of view effects[J]. Applied Optics, 1979, 18(20): 3443–3456. DOI: 10.1364/AO.18.003443 |
| [6] |
徐稚, 杨磊, 向永源, 等. 抚仙湖一米红外太阳望远镜Hα窄带滤光器扫描轮廓的检测与修正[J]. 天文研究与技术——国家天文台台刊, 2014, 11(3): 239–246 Xu Zhi, Yang Lei, Xiang Yongyuan, et al. An investigation of spectral-line profiles from the wavelength-scanning with a narrow-band Hα Lyot filter on the YNAO new vacuum solar telescope[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2014, 11(3): 239–246. |
| [7] |
汤学胜, 毛伟军. 晶体定轴误差对宽视场双折射滤光器视场影响的分析[J]. 天文研究与技术——国家天文台台刊, 2008, 5(2): 206–212 Tang Xuesheng, Mao Weijun. The analysis of effects of optical axis errors on the field of view in the wide-fieldbirefringentfilter[J]. Astronomical Research & Technology-Publications of National Astronomical Observatories of China, 2008, 5(2): 206–212. |
| [8] |
玄伟佳, 王东光, 邓元勇, 等. 双折射滤光器的误差分析与性能优化[J]. 光学精密工程, 2010, 18(1): 52–59 Xuan Weijia, Wang Dongguang, Deng Yuanyong, et al. Error analysis and performance optimization of birefringent filter[J]. Optics and Precision Engineering, 2010, 18(1): 52–59. |
| [9] |
向永源, 刘忠, 金振宇, 等. 高分辨率太阳图像重建方法[J]. 天文学进展, 2016, 34(1): 94–110 Xiang Yongyuan, Liu Zhong, Jin Zhenyu, et al. High resolution solar image reconstruction[J]. Progress in Astronomy, 2016, 34(1): 94–110. DOI: 10.3969/j.issn.1000-8349.2016.01.06 |



