伽玛射线暴(Gamma-Ray Bursts, GRBs)是来自宇宙空间的伽玛射线在短时间内忽然增强的高能爆发现象。它的持续时间一般在0.1 s到1 000 s之间,通常用T90(T90指光子数累积计数从5%到95%)作为典型时标,把伽玛射线暴分为长暴(T90>2 s)和短暴(T90<2 s)两种类型。两类暴可能产生于不同的辐射区域,它们的暴源可能有本质的区别[1]。目前普遍认为长暴起源于大质量恒星的引力塌缩,短暴来源于双中子星或者中子星与黑洞双星系统的并合。引力塌缩或者双星并合都可能形成一个以恒星级黑洞为中心,周围是一个吸积盘的超吸积系统[2]。在吸积系统中,通常可以认为是中微子湮灭过程为伽玛暴提供能量,而一个围绕着恒星级黑洞的具有非常高的吸积率的中微子主导吸积盘(Neutrino Dominated Accretion Flow, NDAF)被认为是伽玛暴中心能源机制的重要候选者[3-4]。中微子主导吸积盘的内区吸积物质具有非常高的密度和温度,质子和光子无法从盘上逃逸。相反,中微子可以带着粘滞产生的热量和大量的引力束缚能从盘上辐射,而它们在盘上的湮灭可能产生初始火球。
文[5]推导了通过中微子提供能量的喷流的最大可能能量,该能量是暴持续时间的函数, 结果证明了这个模型可以为持续时间小于100 s的伽玛暴提供能量,而晚期的X射线耀发和超长伽玛暴很难用这个模型解释。但是,他们忽略了来自于中心机制的活动,以及黑洞的演化,特别是黑洞转速的演化。在中微子主导吸积盘中,中微子辐射和中微子湮灭光度与吸积率、黑洞质量以及黑洞转速紧密相关[6]。如果在伽玛暴的中心,真的存在一个围绕中微子主导吸积盘的恒星级黑洞,那么在这种黑洞超吸积系统中,吸积可能引起黑洞的剧烈演化,黑洞参数不可避免地发生巨大变化,这将进一步影响中微子湮灭光度以及总的中微子能量[6]。首先讨论不同的初始参数下转速的演化,肯定了黑洞的演化引起黑洞参数的巨大变化。接着讨论不同参数下中微子光度和总的中微子能量的演化,分析黑洞参数对中微子光度和能量的影响。最后根据短暴的观测数据计算GRB 090510的中微子能量,并与理论预测值进行比较,分析这种机制解释短暴GRB 090510爆发的可行性。
1 物理模型分析理论上,如果在伽玛暴的中心存在一个超吸积系统,那么黑洞的特征参数将随着时间发生很大的变化。不考虑视界面附近磁场提取旋转能并以poynting能流的形式向外传播的机制(Blandford-Znajek机制, BZ机制),根据能量和角动量守恒公式,可以得到一个Kerr黑洞的演化方程[6]:
| $ \frac{{d{M_{{\rm{BH}}}}}}{{{\rm{d}}t}} = \dot M{e_{\rm{ms}}}, $ | (1) |
| $ \frac{{d{J_{{\rm{BH}}}}}}{{{\rm{d}}t}} = \dot M{l_{{\rm{ms}}}}, $ | (2) |
其中MBH,JBH和
| $ {e_{{\rm{ms}}}} = \frac{1}{{\sqrt {3{\chi _{ms}}} }}\left( {4 - \frac{{3a}}{{\sqrt {{\chi _{{\rm{ms}}}}} }}} \right), $ | (3) |
| $ {l_{{\rm{ms}}}} = 2\sqrt 3 \frac{{G{M_{{\rm{BH}}}}}}{c}\left( {1 - \frac{{2a}}{{3\sqrt {{\chi _{{\rm{ms}}}}} }}} \right), $ | (4) |
其中,a≡cJBH/GMBH2为黑洞的无量纲转速;χms=3+Z2-
根据(1)~(4)式可以得到黑洞转速随时间的演化:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}t}} = 2\sqrt 3 \frac{{\dot M}}{{{M_{{\rm{BH}}}}}}{\left( {1 - \frac{a}{{\sqrt {{\chi _{{\rm{ms}}}}} }}} \right)^2}. $ | (5) |
如果黑洞初始的质量m、转速a和吸积率
| $ {M_{{\rm{disk}}}} = \dot M\frac{{{T_{90}}}}{{1+z}}, $ | (6) |
其中,T90和z分别是暴的持续时间和红移。为了简单方便, 用无量纲化的参数mdisk=Mdisk/M⊙计算。
在中微子主导吸积盘模型中,由于中微子湮灭光度Lvv与黑洞质量MBH、黑洞转速a和吸积率
| $ {L_{{\rm{v\bar v}}}} \approx 1.59 \times {10^{54}}\chi _{{\rm{ms}}}^{ - 4.8}m_{{\rm{BH}}}^{ - 3/2}{\dot m^{9/4}}{\rm{erg}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}, $ | (7) |
对(7)式积分,可以得到中微子总的湮灭能量:
| $ {E_{{\rm{v\bar v}}}} \approx 1.59 \times {10^{54}}\int_0^{T90, {\rm{s/}}\left( {1+z} \right)} {\chi _{{\rm{ms}}}^{ - 4.8}m_{{\rm{BH}}}^{ - 3/2}{{\dot m}^{9/4}}{\rm{d}}{{t}_{\rm{s}}}\;{\rm{erg}}, } $ | (8) |
其中,T90, s=T90/(1s);ts=t/(1s)。
观测上,触发伽玛暴瞬时辐射和余辉的火球能量主要由中微子和反中微子湮灭提供,因此,中微子湮灭总能量Evv等于根据瞬时辐射阶段的观测数据得到的各向同性辐射能量Eγ, iso和长时标余辉能量外流的各向同性动能Ek, iso之和[7-8]。
| $ {E_{{\rm{v\bar v}}}} \approx \frac{{\left( {{E_{{\rm{ \mathsf{ γ} , iso}}}}+{E_{{\rm{k, iso}}}}} \right)\theta _{\rm{j}}^2}}{\eta }, $ | (9) |
其中,η为转化效率;θj为喷流的张角。选取η=0.3,可以从观测数据计算中微子总的湮灭能量。
2 结果和分析根据上面的方程,通过合理地给定黑洞的初始质量m、转速a和吸积率
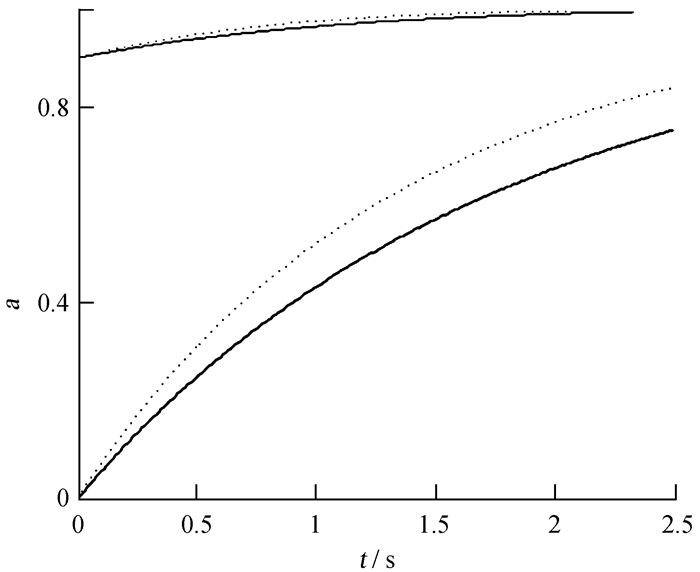
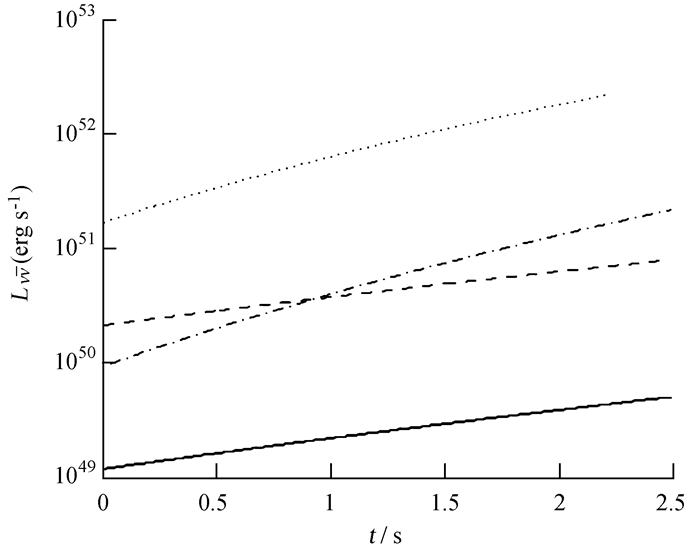
参数选择的合理性是一个至关重要的问题,而盘质量是反应这种模型合理性的一个重要因素。短暴来源于致密双星的并合,因此,黑洞的质量通常小于双星的总质量,即:<4M⊙。双中子星或者黑洞与中子星双星并合的模拟结果表明,盘质量大约在0.2M⊙到0.5M⊙之间[3, 8]。可以合理地假设黑洞初始质量m=2.3和3,盘质量mdisk=0.2和0.5,选取黑洞转速a=0、0.5和0.9。根据(1)式到(5)式得到转速a随时间变化的关系曲线,如图 1。图 1中,初始转速分别取0和0.9,实线和虚线分别表示初始黑洞质量为2.3和3。从图中可以清楚地看到黑洞转速随时间的演化有比较明显的变化。而黑洞的转速对吸积盘质量的影响尤为重要,因此在计算中必须考虑转速的演化。从图中也可以看出黑洞初始质量对转速的演化影响比较小,所以后面的计算中,统一选取黑洞的初始质量为2.3。接着根据(7)式计算中微子湮灭光度的演化,如图 2,图中实线和虚线分别表示吸积率为0.2,初始转速为0.5和0.9的情况,虚点线和点线分别表示吸积率为0.5,初始转速为0.5和0.9的情况。从中可以看到,中微子光度随着时间的演化变化很大,它的最大值可以达到1052erg s-1。
|
| 图 1 黑洞转速a的演化。实线和虚线分别表示初始黑洞质量为2.3和3 Figure 1 Evolution of the spin of BH a. Solid and dashed lines correspond to the initial dimensionless value of BH mass 2.3 and 3, respectively |
|
| 图 2 中微子湮灭光度Lvv的演化。所有线的初始黑洞质量取2.3。实线和虚线分别表示吸积率为0.2,初始转速为0.5和0.9。虚点线和点线分别表示吸积率为0.5,初始转速为0.5和0.9 Figure 2 Evolution of the mean neutrino annihilation luminosity Lvv. All lines correspond to the initial dimensionless value of BH mass 2.3. The solid and dashed lines correspond to the dimensionless mean accretion rate 0.2 and the initial spin of 0.5 and 0.9, respectively. The dashed dotted and dotted lines correspond to the dimensionless mean accretion rate 0.5 and the initial spin of 0.5 and 0.9, respectively |
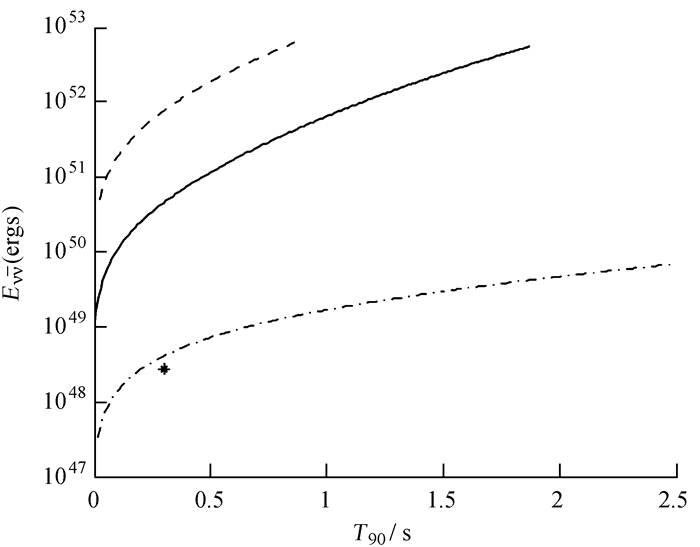
中微子湮灭光度的计算与观测数据不具有直接的相关性。为了进一步检验中微子湮灭模型的合理性,选择短暴GRB 090510的观测数据[7],如表 1,计算了短暴090510的中微子湮灭总能量Evv,并与理论计算分析线比较,如图 3。根据(6)式,选取GRB 090510的T90和z,当mdisk=0.2时,吸积率为1.27。3条线对应的参数分别是虚线:吸积率1.27,初始转速0.9;实线:吸积率1.27,初始转速0.5;虚点线:吸积率0.2,初始转速0.5。星星表示根据GRB 090510的观测数据由(9)式计算的Evv,发现GRB 090510的中微子湮灭总能量的观测值远小于理论预测值,而且初始转速或盘质量取更大值时,吸积率也更大,这时Evv的理论预测值更大。
| GRB | T90 (s) |
Z | Fγ (10-7erg cm-2) |
Fx(11 hours) (10-14erg cm-2 s-1) |
Eγ, iso (1051ergs) |
Ek, iso (1051ergs) |
θj (rad) |
Evv (1048ergs) |
Ref |
| 090510 | 0.3 | 0.903 | 3.4 | 5.04 | 0.73 | 2.15 | 0.017 | 0.028 | (7) |
|
| 图 3 中微子湮灭总能量理论预测值和观测值的比较。3条线黑洞初始质量都为2.3,虚点线表示吸积率为0.2,初始转速为0.5;实线和虚线都是吸积率为1.27,初始转速分别为0.5和0.9,线终止的位置为转速大于0.998的位置,星星表示GRB 090510的观测值 Figure 3 Comparison of the theoretical predictions and observational date of the total annihilation energy. Three lines all correspond to the initial dimensionless value of BH mass 2.3. The dash dot line corresponds to the dimensionless mean accretion rate 0.2 and the initial spin of 0.5; the solid and dashed lines correspond to the dimensionless mean accretion rate 1.27 and the initial spin of 0.5 and 0.9, respectively. The lines truncate when the BH spin has evolved to 0.998. The star denotes the observational result of GRB 090510 |
短暴最有可能起源于双致密星并合,因为这种情形产生的吸积盘较小,持续时间可以和暴的持续时标相当,而围绕着恒星级黑洞的中微子主导吸积盘可以通过盘上发出的中微子湮灭为伽玛暴提供能量。对于这样一个黑洞超吸积系统,盘质量是反应这种模型合理性的一个重要因素,根据短暴的数据,在火球和中微子湮灭模型的框架下,用黑洞的不同参数估算了吸积盘的质量,发现短暴吸积盘的质量主要依赖于输出能量、喷流的张角和黑洞的参数。而黑洞参数中,黑洞的转速和吸积率对盘质量的影响尤为重要[7]。
选取不同的初始黑洞转速和平均吸积率,可以明显地看到转速随时间的变化很大,即:吸积可能引起黑洞特征的极大演化,这会进一步引起中微子光度的演变。进一步讨论了不同吸积率,给定不同黑洞初始参数的情况下,中微子湮灭光度的含时演化以及总的中微子湮灭能量的演化。为进一步讨论这种模型解释伽玛暴瞬时辐射和余辉阶段的可能性,选取了短暴GRB 090510的观测数据,通过观测数据计算了伽玛暴观测的中微子湮灭总能量,并且和理论预测结果相比较,发现GRB 090510的中微子湮灭总能量在理论预测线下方,远小于理论预测值,这可能意味着这个理论模型可以提供GRB 090510爆发所需要的能量。
| [1] |
彭朝阳, 覃一平. 两类γ暴的谱形和光变曲线的统计差异[J]. 天文研究与技术——国家天文台台刊, 2004, 1(2): 77–83 Peng Zhaoyang, Qin Yiping. Statistical distinctions of the spectra and light curves between two classes of gamma-ray bursts[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2004, 1(2): 77–83. |
| [2] | Woosley S E. Gamma-ray bursts from stellar mass accretion disks around black holes[J]. The Astrophysical Journal, 1993, 405(1): 273–277. |
| [3] | Liu T, Hou S J, Xue L, et al. Jet luminosity of gamma-ray bursts:the Blandford-Znajek mechanism versus the neutrino annihilation process[J]. The Astrophysical Journal Supplement Series, 2015, 218: 12(7pp). |
| [4] | Popham R, Woosley S E, Fryer C. Hyperaccreting black holes and gamma-ray bursts[J]. The Astrophysical Journal, 1999, 518(1): 356–374. DOI: 10.1086/apj.1999.518.issue-1 |
| [5] | Leng M B, Giannios D. Testing the neutrino annihilation model for launching GRB jets[J]. Monthly Notices of the Royal Astronomical Society, 2014, 445(1): L1–L5. DOI: 10.1093/mnrasl/slu122 |
| [6] | Song C Y, Liu T, Gu W M, et al. Evolution of stellar-mass black hole hyperaccretion systems in the center of gamma-ray bursts[J]. The Astrophysical Journal, 2015, 815: 54–59. |
| [7] | Liu T, Lin Y Q, Hou S J, et al. Can black-holes neutrino-cooled disks power short gamma-ray?[J]. The Astrophysical Journal, 2015, 806: 58(7pp). |
| [8] | Fan Y Z, Wei D M. Short gamma-ray bursts:the mass of the accretion disk and the initial radius of the outflow[J]. The Astrophysical Journal, 2011, 739: 47(7pp). |


