地基望远镜成像受大气湍流的影响导致图像的闪烁和抖动从而影响图像分辨率^[1], 而高分辨率太阳观测图像是研究太阳物理的必备条件, 这就要求望远镜能够实现衍射极限分辨率的成像^[2]。

目前事后图像处理主要包括盲退卷积、相位差法和斑点统计重建等方法^①。其中斑点统计重建方法的算法本质是基于一组含有高频信息的短曝光图像的统计计算重建目标的高频信息^[3], 如常用的Knox-Thompson (K-T)算法。但是由于观测数据量大、计算复杂等因素的制约, 事后图像重建过程耗时严重, 无法达到实时观测的需求。目前国内外先进的望远镜通常使用高性能计算机或者大规模的计算机集群, 通过并行计算进行高分辨图像重建, 比如美国大熊湖天文台^[4]采用80核的计算集群。但是大规模计算集群的成本太高, 集群规模小处理速度满足不了实时处理的需求, 因此迫切需求一种更高效的方法提高计算效率。

① http://adsabs.harvard.edu/abs/1980itek.rept.....H

近年来图形处理器通用计算技术发展迅猛, 在许多复杂的计算任务中得到广泛应用。本文对CPU-GPU混合架构下的高分辨图像重建进行研究, 系统研究了使用MPI-CUDA混合并行技术实现基于K-T算法的高分辨图像重建的方法, 最终实现了一套在单机环境下的高分辨太阳图像重建系统。

1 混合编程模型 1.1 CUDA简介

图形处理器最早是为提高计算机图形图像显示的实时性和高效性而诞生的, 目前它已发展成为了高密集度、高并行度、多线程、拥有强大计算能力和极高存储器带宽的多核处理器^[5], 其计算能力远远超过了中央处理器, 如NVIDIATeslaK80的单精度计算能力达到了7 TFLOPS。

CUDA (Compute Unified Device Architecture)是一种通用的图形处理器并行计算架构, 该架构利用图形处理器的处理能力能够大幅提升计算性能, 开发人员可以直接使用C语言等在该架构下编写程序。运行在图形处理器上的CUDA并行计算函数称为kernel (内核函数), 一个完整的CUDA程序由一系列的kernel函数和主机端的串行处理部分共同组成。一个kernel函数以线程网格的形式组织, 每个网格由若干个线程块组成, 每个线程块又由若干个线程组成。一个kernel以线程块为单位执行, 只有在同一个线程块中的线程才可以互相通信。CUDA为一些复杂的计算提供了很多应用程序接口, 例如本实验用到的CUBLAS和CUFFT库, CUBLAS库提供了大量对矩阵的基础性操作, CUFFT库提供了一到三维各种数据类型的傅里叶变换函数。

1.2 MPI-CUDA混合编程

MPI是一种消息传递协议, 它通过消息传递实现不同进程之间的通信, 从而达到并行计算的目的。MPI在许多复杂的计算任务中得到广泛应用, 明安图射电频谱日象仪就使用MPI实现了高性能的UVFITS数据合成^[6]。但是MPI的并行仅仅是计算任务的并行, 它将计算任务分成多个子任务同时执行, 从而减小整体的计算时间。如果子任务是数据密集型的计算, 中央处理器的计算能力依然不能满足实时计算的需求。使用MPI实现对任务的划分, 使用CUDA实现对子任务的计算加速, 这就构成了MPI-CUDA混合并行的模式。在中央处理器和图形处理器架构下, 这种模式可以结合两者的优势, 提高科学计算的效率。

2 斑点统计重建方法

斑点统计重建方法是一种以短曝光图像的统计信息为基础的方法, 这种方法通过对目标斑点图像进行某种形式的统计处理得到高分辨重建像^[7]。按重建算法主要分为频域重建和空域重建两类。频域重建的代表方法有基于二阶统计的Labeyrie法^[8], Knox-Thompson (简称K-T)法^[9]和三阶统计的斑点掩膜法^[10]; 空域重建法包括简单位移叠加法、迭代位移叠加法以及基于选帧的相关位移叠加法等。本文采用K-T法实现对太阳图像的高分辨率重建。

2.1 Labeyrie法

在满足等晕性假设下, 每帧短曝光图像i(x)可以看作是目标o(x)和光学点扩展函数h(x)的卷积:

$ i\left( x \right) = o\left( x \right)*h\left( x \right), $

(1)

它的傅里叶变换可以表示为

$ I\left( {\vec f} \right)= O\left( {\vec f} \right) \cdot H\left( {\vec f} \right), $

(2)

其中, $I\left( {\vec f} \right), O\left( {\vec f} \right), H\left( {\vec f} \right)$分别为i(x), o(x), h(x)的傅里叶变换; f为二维空间频率变量。

Labeyrie法也称为斑点干涉术, 是通过统计斑点图的平均能谱复原目标傅里叶振幅。按照Labeyrie的统计方法, 多帧短曝光图像频域幅值平方的系综平均为

$ \left\langle {{{\left| {I\left( {\vec f} \right)} \right|}^2}} \right\rangle = {\left| {O\left( {\vec f} \right)} \right|^2} \cdot \left\langle {{{\left| {H\left( {\vec f} \right)} \right|}^2}} \right\rangle , $

(3)

其中, 中括号〈〉表示算术平均; $\left\langle {{{\left| {H\left( {\vec f} \right)} \right|}^2}} \right\rangle $被称为斑点干涉术传递函数(STF), 退卷积STF可以得到目标的傅里叶振幅。斑点干涉术在统计过程中丢失了相位信息, 只能重建目标的傅里叶振幅, 但是为了完整重建目标, 还需要目标相位。

2.2 K-T法

为了重建目标相位, Knox和Thompson于1974年对Labeyrie法改进后提出了一种基于计算频谱的互相关获取目标相位的方法, 称为Knox-Thompson (简称K-T)法, 又称互谱法。它在统计二阶距时加上一个频率的平移, 则函数的互谱可以表示为

$ C\left( {\vec f, \Delta \vec f} \right) = I\left( {\vec f} \right){I^*}\left( {\vec f + \Delta \vec f} \right), $

(4)

其中, ^*表示共轭; ${\Delta \vec f}$表示空间频率平移量, 当$\Delta \vec f = 0$时, 互谱等同于能谱。对于$\Delta \vec f$的大小, 应该小于$\frac{{{r_0}}}{{\lambda f}}$, 这里r₀为大气相干长度, λ为观测波长, f为系统焦距。

斑点图的互谱统计结果为

$ \left\langle {I\left( {\vec f} \right){I^*}\left( {\vec f + \Delta \vec f} \right)} \right\rangle = O\left( {\vec f} \right){O^*}\left( {\vec f + \Delta \vec f} \right) \cdot H\left( {\vec f} \right){H^*}\left( {\vec f + \Delta \vec f} \right), $

(5)

其中, $H\left( {\vec f} \right){H^*}\left( {\vec f + \Delta \vec f} \right)$为K-T法的传递函数, 它在接近衍射极限截止频率时是一个显著值的实数, 所以互相关谱的相位代表目标各相邻频率处的相位差。通过从零频处的迭代计算其他频率处的相位值。

3 基于MPI-CUDA的K-T图像重建算法实现

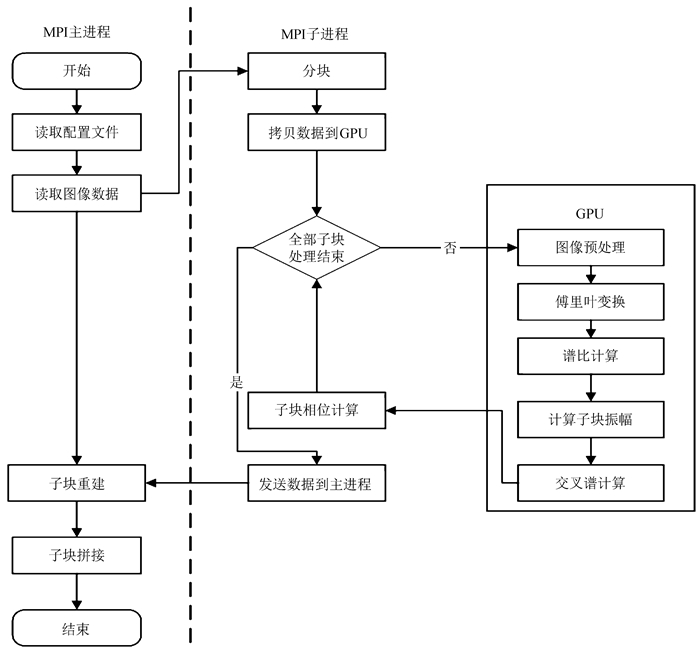
整个系统在单机环境下实现, 计算流程如图 1, 主要由3部分组成:MPI主进程, 若干MPI子进程和图形处理器程序。其中主进程负责分发和汇总数据, 根据振幅和相位重建子图并拼接成完整的视场图。每个子进程负责计算若干子块的振幅和相位, 其中计算过程主要在图形处理器上完成。

3.1 图像预处理和分块

在开始计算之前, 首先要对图像数据进行预处理, 如平场和暗场修正。在成像系统中, 线性空不变很难在一个完整视场内成立, 但是在一个等晕区大小区域内线性空不变近似成立, 可用相同的点扩展函数。因此可以根据等晕区把一组短曝光图像切分成若干个子块, 每个子块可以独立地计算重建振幅和重建相位。最后拼接时只使用子块的中间部分, 因此切分时子块之间有重叠, 本文采用重叠50%。

3.2 数据分发

正是因为子块之间的计算是不相关的, 可以将每个子块的重建看做独立子任务。采用MPI并行计算框架, 实现子块重建的并行化, 将所有子块均衡地分到每个子进程中。为了减少MPI进程间的通信, 尤其是主进程向各个子进程分发数据的时间消耗, 将图像原始数据保存在系统共享内存中。主进程只需向子进程传递一些控制信息, 如子块数据在图像数据的索引位置等, 每个子进程根据索引位置直接从共享内存中读取图像数据, 从而节省大量通信时间。

虽然每个进程只负责子块的计算, 但是子块的计算依然是数据密集的复杂计算。为了进一步对计算进行优化, 利用中央处理器-图形处理器异构计算框架, 在图形处理器中实现数据的并行处理。在开始计算前, 需要将数据拷贝到图形处理器的显存中, 由于主机和图形处理器之间通过PCI总线进行数据传输, 每个子进程需循环处理多个子块, 频繁的进行主机和设备之间数据传输严重影响性能。为了减小对计算性能的影响, 在计算开始前把所有子块的数据拷贝到显存。

3.3 振幅重建

振幅的重建通常在频域使用Labeyrie法退卷积传递函数完成, 每个子块的计算过程如下:

(1) 计算斑点图子块的快速傅里叶变换;

(2) 计算子块的谱比值$\varepsilon \left( {\vec f} \right) = \frac{{{{\left| {\left\langle {I\left( {\vec f} \right)} \right\rangle } \right|}^2}}}{{\left\langle {{{\left| {I\left( {\vec f} \right)} \right|}^2}} \right\rangle }}$;

(3) 通过匹配求得相干长度r₀;

(4) 由r₀计算斑点传递函数$\left\langle {{{\left| {H\left( {\vec f} \right)} \right|}^2}} \right\rangle $;

(5) 通过${\left| {O\left( {\vec f} \right)} \right|^2} = \frac{{\left\langle {{{\left| {I\left( {\vec f} \right)} \right|}^2}} \right\rangle }}{{\left\langle {{{\left| {H\left( {\vec f} \right)} \right|}^2}} \right\rangle }}$, 解卷积得到目标的傅里叶振幅。

首先需要将子块图像从空域转换到频域, 使用CUDA的标准库CUFFT对子块进行傅里叶变换。步骤(2)是整个流程中计算最集中的地方, 其中${{{\left| {\left\langle {I\left( {\vec f} \right)} \right\rangle } \right|}^2}}$需要对子块中的单帧图像求算术平均, 要把频域内所有频率点的值相加, 而求和是数据依赖型计算不利于并行。在每个线程块中的线程可以利用共享内存进行交互和块内线程同步的特性, 采用归约求和的方式, 可以将求和计算的时间复杂度由O(N)降为O(log₂N)。其他各个频率点是独立计算的, 将线程总数设置为频率点总数, 最大地利用图形处理器的并行能力。在大气湍流满足Kolmogorov谱的情况下, 斑点干涉术传递函数只是大气相干长度r₀的函数。通过理论计算不同r₀情况下${\varepsilon _0}\left( {\vec f} \right) = \frac{{{{\left| {\left\langle {H\left( {\vec f} \right)} \right\rangle } \right|}^2}}}{{\left\langle {{{\left| {H\left( {\vec f} \right)} \right|}^2}} \right\rangle }}$的值作为基准, 将步骤(2)计算出来的值与其匹配得到r₀, 根据r₀求出斑点干涉术传递函数, 退卷积斑点干涉术传递函数得到目标的傅里叶振幅。

3.4 相位重建

重建完整的图像只有振幅是不够的, 还需要目标图像的相位。采用K-T法计算得到图像的互相关谱的相位即目标图像的各相邻频域处的相位差, 通过从零频处的迭代得到其他频率处的相位值。每个子块的计算过程如下:

(1) 计算斑点图子块的快速傅里叶变换;

(2) 计算K个不同频移的交叉谱;

(3) 迭代计算K个不同频移下的子块相位;

(4) 对K个相位结果求平均得到最终相位。

为了提高计算的精确度, 对图像进行K个不同的频移并计算它们的交叉谱, 由此带来了计算量的大幅增加, 采用串行的方式对每个频率点进行计算则需要K × N个循环, 可见计算量是巨大的。通过分析, 不同频移的交叉谱计算是独立的, 将线程数设置为与频率点总数相等, 每个线程计算一个频率点的K个不同频移。由互相关谱只能得到相邻频率间的相位差, 要获得目标相位还需要从零频处迭代求和才能得到。频率(m, n)处的相位值可以由不同路径求得, 如分别由频率(m-1, n)和频率(m, n-1)的相位与相对应的相位差求和得到, 为了提高精度, 通常对不同路径的结果求平均。这种数据强依赖型的计算, 每个点的相位都依赖前面的点计算得到, 尚无较好的方法使用图形处理器并行计算。

3.5 图像拼接

根据得到各个子块的目标傅里叶振幅和目标相位, 通过逆傅里叶变换得到重建子图像。重建完子图像后, 需要将所有子图像拼接成全视场的图像。因为使用频域方法重建相位时, 用的是叠加图的初始相位, 所以拼接时一般不会有偏移。拼接完成后, 需要进行一些后续处理, 如图像的对齐等。

4 实验分析

对上述CUDA-MPI的混合模型实现太阳图像高分辨重建过程的性能进行测试。实验采用的计算机配置为IntelXeon-2620v3处理器, 主频为2.4 GHz; 图形处理器为两张英伟达公司的TeslaK80显卡, 每张显卡有两个核芯, 4 992个CUDA核, 12 G显存; 操作系统是Ubuntu14.04.5LTS。测试数据为1 m太阳望远镜观测的100帧短曝光太阳图像, 参数见表 1。

实验中使用不同的进程数, 测试MPI-CUDA和纯MPI两种并行方式实现K-T算法的时间, 由于使用的显卡共有4个计算核芯, 为了使每个核芯的计算任务均衡, 子进程数设置为4的倍数, 结果见表 2。从结果对比可以看出, 只使用一个子进程即串行计算时, MPI-CUDA使得计算速度获得明显提升, 整个流程的计算时间只有后者的1/3, 这表明使用图形处理器优化计算后加速效果明显。随着子进程数目的增加, 并行计算的优势展现出来, 两者的计算时间都大幅减少, 但是MPI-CUDA的计算时间始终快于纯MPI。不过受限于图形处理器和中央处理器的计算能力, 两者的计算时间在达到一个最小值后, 继续增加进程数时间反而增加, 其中MPI-CUDA在使用8个子进程时计算时间最少只有12 s, 而MPI最少时却需要20 s, 因此MPI-CUDA混合并行的方式具有明显优势。

此外在使用8个子进程的前提下, 分别用中央处理器和图形处理器处理子块, 并对各个环节所用的时间进行统计, 结果如表 3。

从时间对比上可以看出, 算法移植到图形处理器上后每一部分都获得了速度提升, 但是各部分的加速比却有所差异, 这和各部分在程序中的具体实现有关, 并行化程度越高加速比越大, 其中计算平均值获得了172.56倍的加速。从时间占用上看, 由于要计算k个不同频移的交叉谱, 交叉谱的计算时间占比最高, 而使用图形处理器加速后获得了5.76的加速比, 在单个子块计算过程中的时间占用也从75.3%下降到了31.1%, 对整个程序的加速起了关键作用。由于递推求相位等数据依赖性强, 计算无法在图形处理器上并行实现, 并且中央处理器还要完成图像拼接等计算流程和逻辑控制流程, 此外中央处理器和图形处理器之间的数据传输也存在时间消耗, 最终使用MPI-CUDA的方式较只使用MPI并行时间缩短了一半。由于图形处理器与中央处理器结构的差异, 大量的浮点数计算使得最后结果存在微小的精度误差, 但是MPI-CUDA混合并行模式得到的重建图像达到了预期效果, 图像的纹理细节得以展现。

5 总结

本文在单机上使用MPI-CUDA混合并行的模式实现了基于K-T算法的太阳高分辨图像重建, 并且取得了预期效果。实验使用不同数目的进程进行测试, 结果表明, 这种混合并行的模式快于纯MPI的并行, 尤其是子块中交叉谱的计算移植到图形处理器后获得了2.4倍的加速, 使整个流程的时间大大减少, 图形处理器的密集运算能力得到了充分体现。天文观测产生的数据量大, 并且数据处理的算法复杂, 中央处理器的计算能力远远不能满足海量数据处理的需要, 而中央处理器-图形处理器这种高性能混合架构为天文研究的大规模计算任务提供了借鉴和参考。在未来的工作中, 需要进一步对算法进行分析和优化, 如在不影响重建效果的情况下, 减小子块的重叠面积, 从而减小子块的数量。加深对图形处理器计算架构的理解, 将更多的计算在图形处理器上完成, 并将MPI-CUDA混合并行的方法推广到采用斑点掩膜法的太阳高分辨图像重建中。