2. 中国科学院国家天文台, 北京 100012
2. National Astronomical Observatory, Chinese Academy of Sciences, Beijing 100012, China
随着微小型飞行器和机器人等的快速发展,对其姿态研究显得越来越重要。一般载体的姿态常常采用滤波器对来自微机械(Micro-Electro-Mechanical System, MEMS)惯性测量单元(IMU)的多传感器数据进行融合得到,常用的微机械惯性测量器件包括三轴陀螺仪、三轴加速度计和三轴磁力计。文[1]建立了四元数卡尔曼滤波方程并进行了数据仿真,文[2]对文[1]提出的四元数卡尔曼滤波进行性能分析。同时很多人也进行了粒子滤波在姿态估计中的研究[3]。文[4]和文[5]通过对四元数的分析,设计了四元数粒子滤波算法求取姿态。本文通过对微机械器件数据采集和处理,设计非线性四元数卡尔曼滤波和粒子滤波,并对其姿态解算结果进行进一步分析。
1 四元数简介载体上的微机械惯性测量器件的输出转换成载体的姿态,即载体自身坐标系(xb, yb, zb)相对于导航坐标系(xn, yn, zn)的角位置,写成矩阵形式如下:
| $ \left[ {\begin{array}{*{20}{c}} {{x_b}}\\ {{y_b}}\\ {{z_b}} \end{array}} \right] = {A_{z - y - x}}\left[ {\begin{array}{*{20}{c}} {{x_n}}\\ {{y_n}}\\ {{z_n}} \end{array}} \right], $ | (1) |
欧拉角是载体的3个姿态角,即俯仰角(Pitch)、横滚角(Roll)和偏航角(Yaw)。根据欧拉旋转定律,可以通过3次旋转使得载体坐标系与导航坐标系重合,每一次旋转都绕导航坐标系的一个坐标轴转动,转过的角度就是欧拉角,每次旋转后坐标关系可由一个旋转矩阵表示,即方向余弦矩阵,(1)式采用z-y-x的旋转顺序依次旋转:
| $ \begin{array}{l} {A_{z - y - x}}\left( {\psi ,\theta ,\varphi } \right) = {A_z}\left( \varphi \right){A_y}\left( \theta \right){A_x}\left( \psi \right) = \\ \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \varphi }&{\cos \theta \sin \varphi }&{ - \sin \theta }\\ {\sin \phi \sin \theta \cos \varphi - \cos \phi \sin \varphi }&{\sin \phi \sin \theta \sin \varphi + \cos \phi \cos \varphi }&{\sin \phi \cos \theta }\\ {\cos \phi \sin \theta \cos \varphi + \sin \phi \sin \varphi }&{\cos \phi \sin \theta \sin \varphi - \sin \phi \cos \varphi }&{\cos \phi \cos \theta } \end{array}} \right], \end{array} $ | (2) |
其中,ψ, φ, θ分别代表偏航角、横滚角、俯仰角。为了避免欧拉角在表示姿态时可能出现的奇异问题,四元数在载体的姿态表示方面有广泛的应用。设计载体姿态四元数为
| $ q = \left( {{q_0},{q_1},{q_2},{q_3}} \right) = {q_0} + {q_1}i + {q_2}j + {q_3}k, $ | (3) |
导航坐标系与载体坐标系之间的坐标变换可以用方向余弦矩阵表示,其四元数形式为
| $ A\left( q \right)_n^b = \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 - q_3^2}&{2\left( {{q_1}{q_2} + {q_0}{q_3}} \right)}&{2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)}\\ {2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)}&{q_0^2 - q_1^2 + q_2^2 - q_3^2}&{2\left( {{q_2}{q_3} + {q_0}{q_1}} \right)}\\ {2\left( {{q_1}{q_3} + {q_0}{q_2}} \right)}&{2\left( {{q_2}{q_3} - {q_0}{q_1}} \right)}&{q_0^2 - q_1^2 - q_2^2 + q_3^2} \end{array}} \right], $ | (4) |
简记为:
| $ A\left( q \right)_n^b = \left[ {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}}&{{T_{13}}}\\ {{T_{21}}}&{{T_{22}}}&{{T_{23}}}\\ {{T_{31}}}&{{T_{32}}}&{{T_{33}}} \end{array}} \right]. $ | (5) |
导航坐标系到载体坐标系的旋转变换过程中坐标系始终保持直角坐标系,所以
| $ \left\{ \begin{array}{l} \theta = - \arcsin {T_{13}}\\ \phi = \arctan \frac{{{T_{23}}}}{{{T_{33}}}}\\ \varphi = \arctan \frac{{{T_{12}}}}{{{T_{11}}}} \end{array} \right.. $ | (6) |
四元数的微分方程如下:
| $ \dot q = \frac{1}{2}q\omega , $ | (7) |
其中,q为描述载体转动的四元数;ω为载体相对导航坐标系的角速度,也表示为四元数的形式:
| $ \omega = 0 + {\omega _x}i + {\omega _y}j + {\omega _z}k, $ | (8) |
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot q}_0}}\\ {{{\dot q}_1}}\\ {{{\dot q}_2}}\\ {{{\dot q}_3}} \end{array}} \right] = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _x}}&{ - {\omega _y}}&{ - {\omega _z}}\\ {{\omega _x}}&0&{{\omega _z}}&{ - {\omega _y}}\\ {{\omega _y}}&{ - {\omega _z}}&0&{{\omega _x}}\\ {{\omega _z}}&{{\omega _y}}&{ - {\omega _x}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{q_0}}\\ {{q_1}}\\ {{q_2}}\\ {{q_3}} \end{array}} \right], $ | (9) |
| $ \dot q = \frac{1}{2}{\phi _w}q. $ | (10) |
通过三轴陀螺仪测量3个轴的角速度就可以实现实时更新四元数的值,进而更新姿态角获得姿态信息。
2 四元数卡尔曼滤波在四元数和非线性滤波算法的结合中,最常用的算法就是基于四元数卡尔曼滤波,本文使用文[1]的四元数卡尔曼滤波,滤波过程简介如下:
(1) 滤波器初始化
为Q和R选取初始值,可以通过对静态下三轴陀螺仪、三轴加速度计和三轴磁力计进行测量,计算出各个轴的方差作为滤波器数据误差;通过初始加速度计测量出俯仰角和横滚角,用磁力计测量出方位角作为初始姿态,并把初始姿态角转变为初始四元数q0/0,选择P0/0=I4作为系统初始噪声。
(2) 状态方程传播
文[1]中的Hamilton算子定义如下:
| $ \bar H\left( q \right) = \left[ {\begin{array}{*{20}{c}} s&{ - {v^T}}\\ v&{s - \left[ {v \times } \right]} \end{array}} \right], $ | (11) |
其中,s表示四元数的标量;v表示四元数的矢量。
| $ \mathit{\Omega }_k^b = \bar H\left( {\omega _{kq}^b} \right), $ | (12) |
| $ {\mathit{\Phi }_{k + 1/k}} = \exp \left( {\frac{1}{2}\mathit{\Omega }_k^b\Delta t} \right), $ | (13) |
| $ {\mathit{q}_{k + 1/k}} = {\mathit{\Phi }_{k + 1/k}}{q_{k/k}}, $ | (14) |
| $ {M_{k/k}} = {q_{k/k}}q_{k/k}^T + P_{k/k}^q, $ | (15) |
| $ P_{k + 1/k}^q = {\mathit{\Phi }_{k + 1/k}}P_{k/k}^q\mathit{\Phi }_{k + 1/k}^T + \frac{1}{4}\left[ {{\rm{tr}}\left( {{M_{k/k}}} \right){I_4} - {M_{k/k}}} \right]{Q_k}. $ | (16) |
(12)式到(16)式中,qk/k为tk时刻将矢量在R系中的投影转到B系中的姿态四元数;ωkqb为tk时刻将B系相对于R系的角速度在B系中的投影;Φk+1/k为姿态转移矩阵;qk+1/k和Pk+1/kq分别代表状态量qk/k的递推估计值和协方差矩阵。
(3) 量测方程更新
首先通过预测得到的qk+1/k应用(4)式计算出观测方程中的系数矩阵H(qk+1/k).
| $ {M_{k + 1/k}} = {q_{k + 1/k}}q_{k + 1/k}^T + P_{k + 1/k}^q, $ | (17) |
| $ {B_{k + 1}} = \bar H\left( {{b_{k + 1}}} \right), $ | (18) |
| $ P_{k + 1/k}^v = \frac{1}{4}{R_{k + 1}}\left[ {{\rm{tr}}\left( {{M_{k + 1/k}}} \right){I_4} - {M_{k + 1/k}} - {B_{k + 1}}{M_{k + 1/k}}B_{k + 1}^T} \right], $ | (19) |
| $ {S_{k + 1/k}} = H\left( {{q_{k + 1/k}}} \right)P_{k + 1/k}^qH{\left( {{q_{k + 1/k}}} \right)^T} + P_{k + 1/k}^v, $ | (20) |
| $ {K_{k + 1}} = P_{k + 1/k}^qH{\left( {{q_{k + 1/k}}} \right)^T}S_{k + 1/k}^{ - 1}, $ | (21) |
| $ {q_{k + 1/k + 1}} = {q_{k + 1/k}} + {K_{k + 1}}\left[ {{b_{k + 1}} - H\left( {{q_{k + 1/k}}} \right){n_{k + 1}}} \right], $ | (22) |
| $ P_{k + 1/k + 1}^q = \left[ {{I_4} - {K_{k + 1}}H\left( {{q_{k + 1/k}}} \right)} \right]P_{k + 1/k}^q. $ | (23) |
在(18)式到(23)式中,bk+1为空间矢量在B系中的投影四元数;Pk+1/kv为计算出来的状态协方差;Kk+1为tk+1时刻的卡尔曼增益系数;qk+1/k+1为tk+1时刻的递推四元数估计;Pk+1/k+1q为四元数卡尔曼滤波方程的观测协方差。
3 粒子滤波粒子滤波是通过寻找一组在状态空间中传播的随机样本近似表示状态变量,用样本均值代替积分运算,进而获得系统最小方差的过程,这些样本被称为粒子。采用数学语言描述如下:对于平稳的随机过程,假设k-1时刻系统的后验概率为p(xk-1|zk-1), 依据一定原则选取n个随机样本,k时刻获得测量更新后,经过状态和时间过程,n个粒子的后验概率密度可近似为p(xk|zk),随着粒子数目的增加,粒子的概率密度函数逐渐逼近状态的概率密度函数,从而粒子滤波达到最优贝叶斯估计的效果[3]。
假设非线性动态离散系统为
| $ \left\{ {\begin{array}{*{20}{c}} {{x_{k + 1}} = {f_k}\left( {{x_k},{w_k}} \right)}\\ {{z_k} = {h_k}\left( {{x_k},{v_k}} \right)} \end{array}} \right., $ | (24) |
其中,xk∈Rn为k时刻的n维状态向量;zk∈Rm为m维观测向量;wk和vk分别为过程噪声和量测噪声。
粒子滤波算法步骤如下:
(1) 初始化:k=0时,产生服从初始概率密度p(x0)的N个粒子点x0(i), i=1…n;
(2) 通过重要性采样更新样本粒子状态,
| $ \bar x_k^{\left( i \right)} \sim q\left( {{x_k}\left| {x_{0:k - 1}^{\left( i \right)},{z_{1:k}}} \right.} \right), $ | (25) |
| $ \bar x_{0:k}^{\left( i \right)} = \left( {x_{0:k - 1}^{\left( i \right)};\bar x_k^{\left( i \right)}} \right),i = 1 \cdots N. $ | (26) |
(3) 计算更新后粒子的权值
| $ w_k^{\left( i \right)} = w_{k - 1}^{\left( i \right)}\frac{{p\left( {{z_k}\left| {x_k^{\left( i \right)}} \right.} \right)p\left( {x_k^{\left( i \right)}\left| {x_{k - 1}^{\left( i \right)}} \right.} \right)}}{{q\left( {x_k^{\left( i \right)}\left| {x_{0:k - 1}^{\left( i \right)},{z_{1:k}}} \right.} \right)}}. $ | (27) |
(4) 归一化粒子权值
| $ w_k^{\left( i \right)} = w_k^{\left( i \right)}/\sum {w_k^{\left( i \right)}} . $ | (28) |
(5) 重采样:根据各自归一化权值wk(i)的大小复制/舍弃样本,得到N个近似服从p〈(x0:k(i))|(z1:k〉分布的样本x0:k(i),令
(6) 输出结果:算法的输出是粒子集{x0:k(i), i=1…N}, 用它可以表示后验概率和函数g(x0:k)的期望:
| $ p\left( {{x_{0:k}}\left| {{z_{1:k}}} \right.} \right) = \frac{1}{N}\sum {\delta x_{0:k}^{\left( i \right)}\left( {d{x_{0:k}}} \right)} , $ | (29) |
| $ E\left[ {g\left( {{x_{0:k}}} \right)} \right] = \frac{1}{N}\sum {{g_k}\left( {x_{0:k}^{\left( i \right)}} \right)} . $ | (30) |
(7) 令k=k+1, 重复以上步骤。
4 数据实验实验通过选择传感器模块mpu9250,它包含三轴陀螺仪、三轴加速度计和三轴磁力计,能够通过自身所有的低通滤波器和A/D变换模块直接输出九轴传感器数据。实验通过将mpu6050固定在转台上测量,在安装过程中远离环境磁场的干扰。采用单片机读取mpu9250测量数据后通过I2C串口传输给电脑进行处理,以检验算法的可用性和精度。
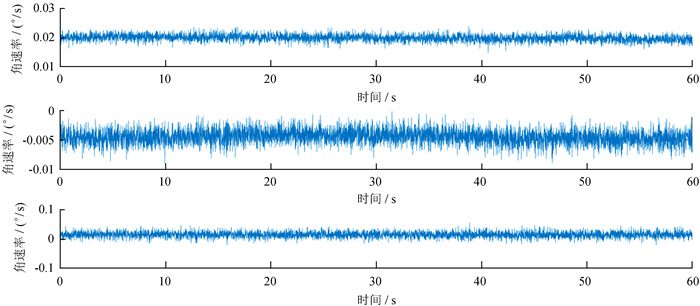
(1) 首先将传感器模块mpu9250在静止状态下测量输出数据,采样速率为100 Hz,采样1 min,分析静态情况下的九轴输出数据。陀螺仪三轴静态数据如图 1。
|
| 图 1 陀螺仪三轴静态输出数据 Figure 1 Three-axis gyroscope static output data |
图 1是1 min采集的陀螺仪三轴数据,自上而下依次是x轴、y轴和z轴,运用MATLAB软件分析x轴的均值和方差分别为:0.0205(°)/s和1.238e(-4)(°)/s;y轴的均值和方差分别为:-0.004 8(°)/s和1.57e(-4)(°)/s;z轴的均值和方差分别为:0.015 4(°)/s和2.369 9e(-4)(°)/s。用同样的方法处理三轴加速度计和三轴陀螺仪的原始数据,结果见表 1。
| 三轴加速度计/g | 三轴磁力计/uT | ||||||
| x轴 | y轴 | z轴 | x轴 | y轴 | z轴 | ||
| 均值 | 0.4 | -0.5 | 9.4 | 3.6 | 4.5 | 2.1 | |
| 方差 | 0.002 7 | 0.003 3 | 0.003 1 | 0.02 | 0.096 | 0.01 | |
通过以上测量,加速度计在水平位置x轴和y轴均值不为0,所以在做姿态解算时引入均值误差提高测量精度。
(2) 通过上面静态数据的读取,将各个传感器的方差作为四元数卡尔曼滤波和粒子滤波程序的方差参考,静止状态下四元数卡尔曼滤波和粒子滤波的姿态角结算误差如图 2、图 3。其中横坐标表示时间,单位是秒;纵坐标表示输出的角度误差,单位是(°)

|
| 图 2 四元数卡尔曼滤波静态三轴姿态角误差 Figure 2 Quaternion Kalman filter static triaxial attitude angle error |
|
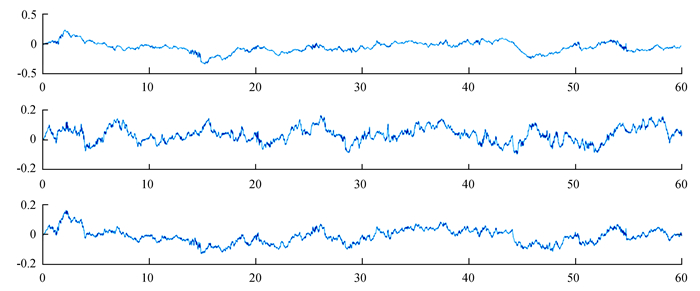
| 图 3 粒子滤波静态三轴姿态角误差 Figure 3 Particle filter static triaxial attitude angle error |
静止状态下四元数卡尔曼滤波和粒子滤波三轴姿态角均值和误差如表 2。通过对静态数据的分析可以看出,两种算法对均值改善相差不多,但是粒子滤波比四元数卡尔曼滤波在方差上有所改善,即粒子滤波静态测量相对稳定。
| 四元数卡尔曼 | 粒子滤波 | ||||||
| x轴 | y轴 | z轴 | x轴 | y轴 | z轴 | ||
| 均值 | 0.002 | 0.003 6 | 0.002 7 | -0.033 7 | 0.036 9 | 0.001 6 | |
| 方差 | 0.010 6 | 0.008 7 | 0.010 1 | 0.014 3 | 0.002 4 | 0.004 5 | |
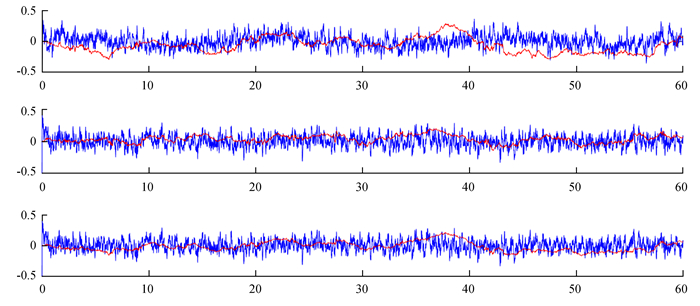
(3) 由于没有转台等实验设备,通过对静态数据添加一个稳定的姿态仿真轨迹计算四元数卡尔曼滤波和粒子滤波在动态情况下的结算结果。通过对三轴姿态角分别添加角速率为2,3,5(°)/s,幅度为5仿真,得到如图 4的仿真结果。其中横坐标表示时间,单位是秒;纵坐标表示输出的角度误差,单位是(°)
|
| 图 4 两种算法姿态角误差比较 Figure 4 Comparison of Attitude Angle Errors of Two Algorithms |
从表 3可以看出,通过对动态的仿真实验分析,两种算法在均值改善和静态数据基本相同,但是粒子滤波比四元数卡尔曼滤波在方差上有所改善,即动态情况下粒子滤波相对稳定。
| 四元数卡尔曼 | 粒子滤波 | ||||||
| x轴 | y轴 | z轴 | x轴 | y轴 | z轴 | ||
| 均值 | 0.030 1 | 0.020 1 | 0.025 4 | -0.034 7 | 0.018 0 | 0.020 4 | |
| 方差 | 0.014 | 0.009 5 | 0.013 4 | 0.016 1 | 0.005 0 | 0.008 5 | |
本文通过对四元数卡尔曼滤波和粒子滤波进行简单介绍,并通过对mpu9250进行数据采集和仿真实验,验证粒子滤波和四元数卡尔曼滤波的可行性,以误差均值和标准差为检验标准,验证了粒子滤波相对四元数卡尔曼滤波提高了标准差。
| [1] | Choukroun D, Bar-Itzhack I Y, Oshman Y. Novel quaternion Kalman filter[J]. IEEE Transactions on Aerospace and Electronics Systems, 2006, 42(1): 174–190. DOI: 10.1109/TAES.2006.1603413 |
| [2] |
高显忠, 侯中喜, 王波, 等. 四元数卡尔曼滤波组合导航算法性能分析[J]. 控制理论与应用, 2013, 30(2): 171–177 Gao Xianzhong, Hou Zhongxi, Wang Bo, et al. Quaternion-based Kalman filter and its performance analysis in integrated navigation[J]. Control Theory & Applications, 2013, 30(2): 171–177. |
| [3] | 梁军. 粒子滤波算法及其应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10213-2010031031.htm |
| [4] |
乔相伟, 周卫东, 吉宇人. 基于四元数粒子滤波的飞行器姿态估计算法研究[J]. 兵工学报, 2012, 33(9): 1070–1075 Qiao Xiangwei, Zhou Weidong, Ji Yuren. Study on aerial vehicle attitude estimation based on quaternion particle filter algorithm[J]. Acta Armamentarii, 2012, 33(9): 1070–1075. |
| [5] |
吴海亮, 王惠南, 陈志明, 等. 基于粒子滤波的微小卫星姿态确定算法[J]. 中国惯性技术学报, 2007, 15(4): 427–430 Wu Hailiang, Wang Huinan, Chen Zhiming, et al. Particle filtering-based algorithm for micro-satelliteattitude determination[J]. Journal of Chinese Inertial Technology, 2007, 15(4): 427–430. |


