2. 中国科学院空间天文与技术重点实验室, 北京 100012;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Space Astronomy and Technology, Chinese Academy of Sciences, Beijing 100012, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
光学综合孔径技术,又称光学合成孔径技术,是将多个较小口径的光学元件或光学系统进行精确的排列,使通过各子孔径的光束在焦平面上满足一定的同相位条件,实现相干叠加,经图像复原处理后,达到与单一较大通光口径相当的衍射极限分辨率的技术。
H. Fizeau最早在1868年提出恒星光干涉技术,希望利用干涉法测量恒星的角直径。1874年,Steven通过在Large Foucault望远镜前增加掩膜的方法,首次成功观测到恒星的干涉条纹。到目前为止,世界上已经建立了多个拼接子望远镜的光学综合孔径实验系统。美国麻省理工学院(Massachusetts Institute of Technology, MIT)2002年研制的GOLAY-3型光学卫星地面样机(ARGOS)[1],演示验证了空间光学综合孔径技术的可行性,其等效孔径为0.62m,角分辨率为0.35″(优于单个子孔径的角分辨率0.55″),视场角约为3′①。美国洛克-马丁公司研制的Star9装置[2]是由9个子孔径组成的Fizeau型光学综合孔径望远镜,单子孔径为125 mm,经过共相位干涉,实现了与610 mm口径衍射极限相当的分辨率,视场大小为1 urad。
① http://dspace.mit.edu/handle/1721.1/39262
北京理工大学于2009年成功研制了共相位检测与控制平台,对拼接镜面成像系统闭环控制,最终形成干涉条纹[3]。我国自主研制的LAMOST望远镜于2009年竣工验收,采用主动光学技术,有34块拼接主镜和28块拼接施密特校正板,但是只实现了共焦成像,分辨率仍然受限于单子镜的口径。中国科学院西安光学精密机械研究所于2011年进行了综合孔径实验系统的搭建,开展了理论分析、仿真研究和有限距离综合孔径原理验证实验。上海天文台也于2011年建成2个望远镜组成的综合孔径成像系统,采用棱锥波前探测,但未实现共相成像。与国外相比,我国的天文光干涉技术有待进一步发展。
光学综合孔径望远镜各子孔径间达到共相时才能形成干涉,实现复振幅的叠加,提高空间分辨率,否则,只是光强叠加,系统分辨率仍受限于子孔径的衍射极限。因此,各光束间光程差的精确探测对光学综合孔径望远镜光干涉的实现至关重要。
目前国内外发展了多种光程探测的方法。离焦面检测:(1) 曲率传感法[4]通过测量子镜边缘的相位不连续性重构子镜间的光程差误差;(2) 相位恢复法[5]通过焦面和一对离焦面的光强数据反解瞳面相位分布计算光程差误差。出瞳面检测:四棱锥波前检测法[6]通过检测4个出瞳像点能量差异计算光程差误差。焦面检测法:(1) 加州大学Gary Chanan提出的宽带哈特曼-夏克法和窄带哈特曼-夏克法,通过采样孔径的衍射图样与样板图样的相关系数计算拼接子镜间的光程差误差[7];(2) 詹姆斯韦伯太空望远镜使用了色散条纹法[8],通过处理相邻子孔径间色散干涉条纹,对光强分布进行拟合,得到光程差误差。
国家天文台承担了863计划光学稀疏综合成像系统原理样机和综合数据处理技术的课题,本文以此为背景,对光程差探测方法开展了理论和实验研究。针对系统的情况,选择色散条纹法探测一个波长范围内的光程差。在分析双孔干涉理论和仿真模拟的基础上,讨论了光程差与干涉条纹光强纵向峰值偏移量之间的关系,搭建了实验装置,通过处理干涉条纹得到了光程差,并对实验误差进行了系统分析,找到了影响计算精度的主要原因是运动平台的俯仰起伏,为后续改进指明了方向。
1 理论基础双圆孔在望远镜焦平面处,经沿x方向色散的AMICI棱镜,形成的干涉图样强度分布[3]为
| $ I\left( {x, y} \right) = 2{\left( {\frac{{{\rm{π }}{a^2}}}{{\lambda f}}} \right)^2}{\left[{\frac{{2{J_1}\left( Z \right)}}{Z}} \right]^2}\left\{ {1 + \cos \left[{\frac{{2{\rm{π }}}}{{\lambda \left( x \right)}}\left( {\frac{{{\rm{d}}y}}{f} + \phi } \right)} \right]} \right\}, $ | (1) |
其中,Z=2πar/λf;a为圆孔半径;
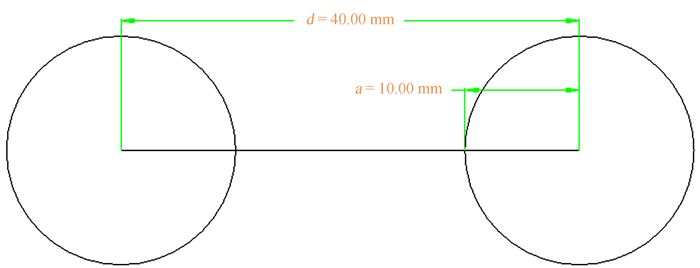
Fizeau型光干涉系统中光程差探测部分双圆孔示意图如图 1,其中参数为:圆孔半径a=10 mm;基线长度d=40 mm;焦距f=1680 mm。
|
| 图 1 两圆孔参数 Figure 1 The parameter of two circle holes |
先讨论单波长下的光干涉,令x=0,则Z=2πay/λf,此时只需要对干涉条纹纵向(y方向)的光强分布进行分析:
| $ {I_f}\left( y \right) = 2{\left( {\frac{{{\rm{\pi }}{a^2}}}{{\lambda f}}} \right)^2}{\left[{\frac{{2{J_1}\left( {\frac{{{\rm{2\pi }}ay}}{{\lambda f}}} \right)}}{{\frac{{{\rm{2\pi }}ay}}{{\lambda f}}}}} \right]^2}\left\{ {1 + \cos \left[{\frac{{2{\rm{\pi }}}}{\lambda }\left( {\frac{{{\rm{d}}y}}{f} + \phi } \right)} \right]} \right\}. $ | (2) |
在-λ/2~+λ/2之间,自变量光程差ϕ与因变量峰值偏移量ymax之间的关系(其中Imax为峰值光强):
| $ \frac{{\lambda f}}{{2d{\rm{\pi }}}}{\rm{arccos(}}\frac{{{I_{\max }}}}{{{{\left[{\frac{{2{J_1}\left( {\frac{{{\rm{2\pi }}a\;{y_{\max }}}}{{\lambda f}}} \right)}}{{\frac{{{\rm{2\pi }}a\;{y_{\max }}}}{{\lambda f}}}}} \right]}^2}}} -1) -{y_{\max }} = \frac{f}{d}\phi . $ | (3) |
假设自变量光程差ϕ在一个波长范围内,此时ϕ与峰值偏移量ymax之间存在线性关系:
| $ \frac{{{y_{\max }}}}{\phi } = K\left( {常数} \right). $ | (4) |
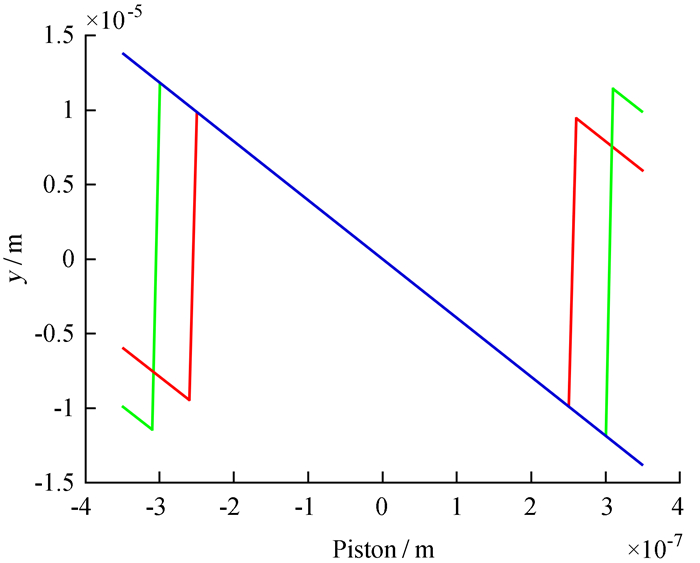
将系统参数代入(4) 式,分别计算500 nm(红)、600 nm(绿)、700 nm(蓝) 3种单波长干涉条纹纵向光强峰值偏移量ymax(下面用y代替)与光程差ϕ(下面用piston代替)之间的关系。利用MATLAB进行数值模拟,计算结果如图 2,其中横坐标光程差的采样间隔为10 nm,纵坐标y为各光程差下干涉条纹纵向光强对应的峰值位置。取线性相关系数r[9]定义如下:
|
| 图 2 峰值偏移量与光程差之间的关系(3种波长) Figure 2 Relationship between y and piston (single-wavelength) |
| $ {r_{xy}} = \frac{{{l_{xy}}}}{{\sqrt {{l_{xx}}{l_{yy}}} }}, $ | (5) |
其中,
在3种单波长条件下,计算K和r值,均得到K≈-39.51,线性相关系数r优于99.99%。因此,可认为在单色光干涉时,光程差在一个波长范围内与y满足线性关系,并且不同波长对斜率的影响较小。
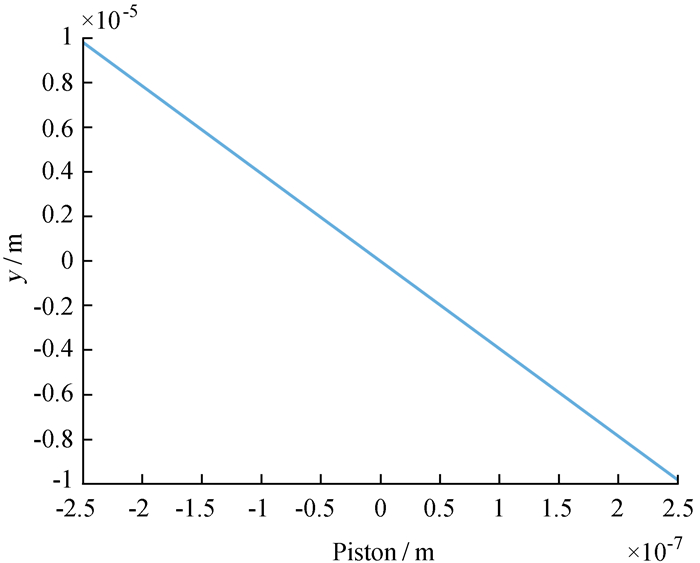
对多波长色散干涉条纹进行分析,假设线色散关系x=2×104(λ-650×10-9)(单位:m),波长λ=600~700 nm,采样间隔Δλ=1 nm,光程差piston=-250 nm~250 nm范围内,得到光程差与峰值偏移量y的拟合曲线如图 3,直线拟合得到斜率K≈-39.37(K=y/piston),线性相关系数r≈99.9999%。因此多波长光形成的色散干涉条纹纵向光强峰值位置y与光程差也呈线性关系,斜率与单波长情况基本相同。
|
| 图 3 峰值偏移量与光程差之间的关系(多波长) Figure 3 Relationship between y and piston (multi-wavelength) |
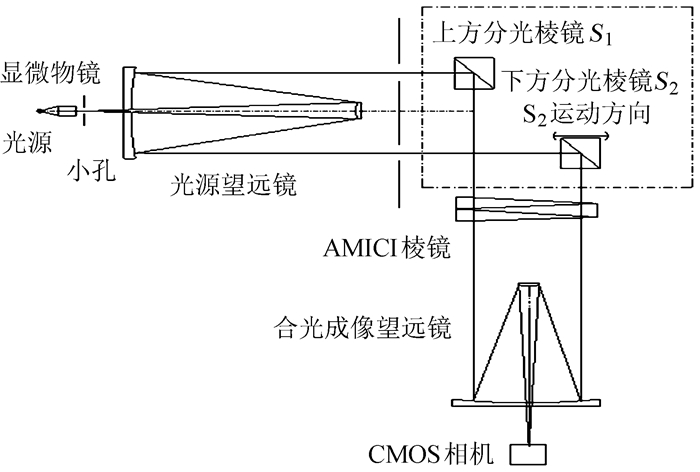
在实验室搭建实验装置如图 4。实验系统由5部分组成:(1) NKT白光光源;(2) 光源望远镜和合光成像望远镜;(3) 分光棱镜S1,S2;(4) AMICI棱镜;(5) CMOS相机(2048×1088像元)。系统光路示意图见图 5。分光棱镜S1位置保持不变,S2安装在直线运动导轨(LPS-45) 上,可通过计算机控制S2运动改变光程差。实验采集的零光程干涉条纹图像如图 6。

|
| 图 4 实验室系统搭建照片 Figure 4 Picture of experimental system |
|
| 图 5 系统光路示意图 Figure 5 Sketch map of system |

|
| 图 6 零光程干涉条纹 Figure 6 Interferometric fringe of piston zero |
根据y与光程差线性相关的仿真结果,在-250 nm~+250 nm范围内,以10 nm为采样间隔,分别采集不同光程差下的色散干涉条纹,并进行数据处理。为了减小误差,对各干涉条纹均取n组纵向(垂直于色散方向)光强数据,分别进行拟合得到峰值位置偏移量y1,y2,…,yn,求其均值得到y。
图 7为实验中一组干涉条纹纵向光强峰值偏移量y与光程差的拟合结果。其中,横坐标光程差的范围是-250 nm~+250 nm,纵坐标y为干涉条纹纵向光强峰值偏移量的均值。线性拟合得到的线性相关系数r=99.81%,斜率K=-50.74。

|
| 图 7 干涉条纹峰值偏移量与光程差拟合结果(实验结果) Figure 7 Relationship between y and piston (result of the experiment) |
通过上述结果可以看出,实验数据处理与仿真计算得到的斜率之间存在一定程度的偏差。接下来对系统的主要误差源进行分析。
4 误差分析 4.1 系统主要参数对斜率的影响为了分析系统各主要设计参数对拟合斜率K的影响,利用MATLAB建立多波长色散干涉模型,分别分析了合光成像望远镜焦距f、圆孔半径a和基线长度d的变化对斜率K的影响。光源波长范围设定在600~700 nm,结果见表 1、表 2。
| d | 39 mm | 40 mm | 41 mm |
| f=1580 mm | -37.86 | -37.04 | -36.25 |
| f=1680 mm | -40.24 | -39.37 | -38.54 |
| f=1780 mm | -42.62 | -41.70 | -40.82 |
| d | 39 mm | 40 mm | 41 mm |
| a=9 mm | -40.76 | -39.86 | -39.00 |
| a=10 mm | -40.24 | -39.37 | -38.54 |
| a=11 mm | -39.69 | -38.86 | -38.05 |
从表 1、表 2可以看出,合光成像望远镜焦距f在±100 mm误差范围内,造成斜率变化范围在±2以内;圆孔半径a在±1 mm误差范围内,造成斜率变化范围约±0.5以内;基线长度d在±1 mm误差范围内,造成斜率变化范围±1以内。可见,以上3个系统参数对斜率的影响较小,不是实验中影响斜率的主要因素。
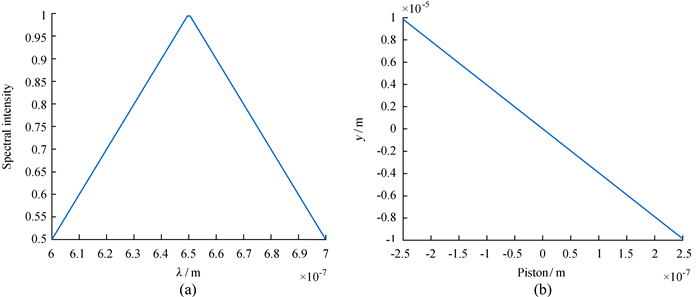
4.2 光源光谱曲线对斜率的影响NKT白光光源的光谱曲线中,各个波长的光强度值均有所差异。为了模拟光谱曲线对色散条纹的影响,假设了两组光谱曲线:(1) 各波长的光强满足均匀随机分配(以0.5~1之间的随机数为比例进行分配),(2) 各波长的光强按一定规律进行分配(光谱曲线见图 8(a),仿真计算结果如图 8(b))。仿真结果显示:两组光谱曲线下得到的y与光程差之间的斜率K均为-39.37,线性相关系数r为99.9999%,并且与各波长光强相同时表现一致。因此,光谱曲线也不是造成斜率变化的原因。
|
| 图 8 (a)光谱曲线;(b)仿真结果的影响 Figure 8 (b) The simulation results under the influence of (a) spectral curve |
带动分光棱镜S2运动的压电陶瓷线性运动平台是PI公司的LPS-45,其最大行程13 mm(±6.5 mm),双向可重复性为±18 nm,最小运动增量为6 nm,角度扰动(pitch&yaw)为±50 urad。在实验系统中,俯仰角度扰动使条纹发生上下偏移,偏航角度扰动使条纹发生左右偏移。首先,对两束光之间存在左右、上下错位的情况进行仿真,结果显示:
(1) 两束光左右错位(Xshift)-4 μm~+4 μm:光程差为0时,色散干涉条纹纵向光强峰值偏移量的最大值约为0.01 nm;光程差为+100 nm时,与未发生左右错位情况下色散干涉条纹纵向光强峰值偏移量之差的最大值约为0.1 nm。可见,左右错位对色散干涉条纹光强峰值偏移量的影响较小。
(2) 两束光上下错位(Yshift)-4 μm~+4 μm:光程差为0时,色散干涉条纹纵向光强峰值位置偏移量随着Yshift的增加而增加,偏移量最大值约为122 nm;光程差为+100 nm时,色散干涉条纹纵向光强峰值位置偏移量随着Yshift的增加而增加,与未发生上下错位情况下色散干涉条纹纵向光强峰值偏移量之差的最大值约为126 nm。可见,上下错位对色散干涉条纹光强峰值偏移量的影响较大。
假设两色散条纹在0光程差下相互重合,通过S2运动产生+10 nm光程差,同时引入上下错位-4 μm~+4 μm,发现斜率值K变化很大,为-27.20~-51.45(如表 3)。实验结果表明,在运动平台最大行程内移动S2将导致探测器上的色散条纹发生上下偏移l=±27.75像素,对应光束角度变化α=l5.5 μm/f=±90.8 urad,S2角度变化α/2=±45.4 urad(在±50 urad内),与系统标称的数据相符。因此,可以判断上下错位是造成实验数据与仿真结果斜率值之间存在较大偏差的主要原因,这是由运动平台的俯仰角度误差决定的。
| 上下错位/μm (上移为正, 下移为负) |
斜率K |
| -4 | -27.20 |
| -2 | -33.25 |
| 0 | -39.32 |
| 2 | -45.40 |
| 4 | -51.45 |
文中主要介绍了使用色散条纹法对光程差进行探测的方法和实验结果。首先,数值计算显示,光程差在一个波长范围内与色散干涉条纹纵向光强峰值偏移量之间存在良好的线性关系。其次,搭建实验光路,开展实验研究,通过控制分光棱镜S2运动改变两光束间的光程差,再对采集的色散干涉条纹进行数据处理得到斜率数据,发现与仿真得到的斜率值有较大偏差。经过较全面的误差分析,分别对主要系统参数、光源光谱曲线和分光棱镜运动引入的角度扰动进行了分析,结果显示分光棱镜运动过程中引入的俯仰角度误差导致的条纹上下偏移是实验数据与仿真计算斜率值偏差较大的主要原因。
针对这一问题,希望用系统标定的方式进行修正。即利用双频激光位移干涉仪对运动棱镜位置进行精确测量(分辨率达1 nm),以此对棱镜位置进行标定,进而得到经标定的斜率K0。在实验中,用标定的K0对光程差进行求解:piston=y/K0。
| [1] | Chung S J, Miller D W, Weck O L D. ARGOS testbed:study of multidisciplinary challenges of future spaceborne interferometric arrays[J]. Optical Engineering, 2004, 43(43): 2156–2167. |
| [2] | Kendrick R L, Aubrun J N, Bell R, et al. Wide-field Fizeau imaging telescope:experimental results[J]. Applied Optics, 2006, 45(18): 4235–4240. DOI: 10.1364/AO.45.004235 |
| [3] | 王姗姗. 基于色散瑞利干涉原理的piston误差检测方法研究[D]. 北京: 北京理工大学, 2009. |
| [4] | Chanan G A, Troy M, Sirko E. Phasing the Keck Telescope with out-of-focus images in the infrared[C]//Larry M. Advanced Technology Optical/IR Telescopes Ⅵ:Proceedings of SPIE. 1998:632-642. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=945267 |
| [5] | Redding D C, Basinger S A, Cohen D, et al. Wavefront control for a segmented deployable space telescope[C]//Breckinridge J B, Jakobsen P. The International Society for Optical Engineering:Proceedings of SPIE. 2000:546-558. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=900353 |
| [6] | Esposito S, Devaney N. Segmented telescopes co-phasing using Pyramid Sensor[C]//Vernet E, Ragazzoni R, Esposito S, et al. 2002 ESO Conference and Workshop Proceedings. Germany:European Southern Observatory, 2002:161. http://adsabs.harvard.edu/abs/2002ESOC...58..161E |
| [7] | Chanan G A, Troy M, Ohara C M. Phasing the primary mirror segments of the Keck telescopes:a comparison of different techniques[C]//Philippe Dierickx. Optical Design, Materials, Fabrication, and Maintenance:Proceedings of SPIE. 2002:188-202. http://spie.org/Publications/Proceedings/Paper/10.1117/12.391510 |
| [8] | Fang S, King B M, Sigrist N, et al. NIRCam long wavelength channel grisms as the dispersed fringe sensor for JWST segment mirror coarse phasing[C]//Oschmann J M, Graauw J D, Mattheus W M, et al. Space Telescopes and Instrumentation 2008:Optical, Infrared, and Millimeter:Proceedings of SPIE. 2008. http://spie.org/Publications/Proceedings/Paper/10.1117/12.789641 |
| [9] | 数学手册编写组. 数学手册[M]. 北京: 高等教育出版社, 2006: 836-840. |


