2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着卫星导航技术的发展,世界各大国相继建设了各自的全球卫星导航系统(Global Navigation Satellite System, GNSS)或区域卫星导航系统,例如美国全球定位系统、俄罗斯GLONASS、欧盟伽利略、中国北斗系统。全球卫星导航系统的空间信号质量不仅直接影响着卫星导航系统定位、导航和授时(Positioning, Navigation and Timing, PNT)的性能,而且能够反映卫星有效载荷的在轨状态与各种电性能指标,因此,全球卫星导航系统空间信号质量是衡量卫星导航系统优劣的一个重要指标,相应的信号质量评估技术可以为信号设计、信号在轨测试以及信号在轨监测提供重要支撑,从而为系统故障诊断和空间信号完好性监测等提供重要保障[1]。
由于全球卫星导航系统空间信号评估是系统设计阶段与运行过程中的一项重要工作,因而引起了各国的高度重视,也是当前卫星导航领域的一个研究热点。目前,全球定位系统、北斗系统和伽利略等卫星导航系统均建立了配套的空间信号质量监测和分析系统,如全球定位系统由美国斯坦福国际研究院建立了导航信号监测和特性分析系统,该系统利用47 m大口径抛物面天线对全球定位系统空间信号进行全天候实时监测[2];伽利略由欧洲空间技术研究中心导航实验室建设了导航信号特性分析系统,该系统由全向天线、标准测量仪器和测试接收机等设备组成[3];北斗系统由中国科学院国家授时中心搭建了全球卫星导航系统空间信号分析平台,以标准测量仪器分析、离线数据评估与监测接收机3种方式对包括北斗系统空间信号在内的多种全球卫星导航系统信号质量进行监测和评估[1, 4]。
离线数据分析一方面根据基带信号分析卫星在短时期内的工作状态[5],另一方面通过监测接收机测量数据对卫星的长期工作性能进行评估[6-7]。本文主要研究基于监测接收机观测量的卫星导航信号稳定性分析方法。
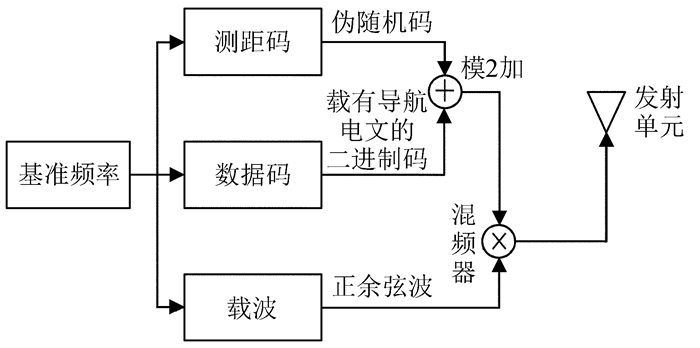
1 卫星导航信号构成通过简要描述全球卫星导航系统发射的信号大致了解卫星导航信号的组成与特点。导航卫星发射的信号从结构上可分为测距码(伪随机码)、载波与数据码三个层次[8]。在卫星发射信号之前,先对数据码与测距码进行调制,然后再将调制信号和正弦波形式的载波混频,最后卫星把调制后的载波信号发射出去。图 1描述了导航卫星信号的基本构成。
|
| 图 1 导航卫星信号构成示意图 Figure 1 Diagram of composition of navigation satellite signals |
在卫星信号接收终端,全球卫星导航系统接收机根据接收的卫星信号输出伪距(依据测距码相位测量得到的伪距也称作测码伪距)与载波相位(依据载波相位测量得到的伪距也称作测相伪距)两个基本观测量。下面介绍伪距和载波相位两个基本观测量的观测方程。
全球卫星导航系统接收机要实现定位、导航或者授时,必须准确测量卫星与接收机之间的距离。伪距和载波相位是接收机对观测卫星的两个基本距离观测量。伪距和载波相位一旦发生中断或者跳变,定位、导航和授时精度都不可避免地受到影响。伪距P和载波相位L的观测方程可分别表示为
| $ \mathit{P}=\rho _{\rm{r}}^{\rm{s}}+c\left( \delta {{t}_{\rm{r}}}-\delta {{t}^{\rm{s}}} \right)+T_{\rm{r}}^{\rm{s}}+I_{\rm{r}}^{\rm{s}}+\varepsilon _{\rm{r, P}}^{\rm{s}}, $ | (1) |
| $ \mathit{L}=\rho _{\rm{r}}^{\rm{s}}+c\left( \delta {{t}_{\rm{r}}}-\delta {{t}^{\rm{s}}} \right)+T_{\rm{r}}^{\rm{s}}-I_{\rm{r}}^{\rm{s}}+\lambda N_{\rm{r}}^{\rm{s}}+\varepsilon _{\rm{r, L}}^{\rm{s}}. $ | (2) |
其中,ρrs为卫星信号发射时刻的卫星位置到信号接收时刻的接收机位置的距离;δtr和δts分别为接收机时钟钟差和卫星时钟钟差;Trs和Irs分别为对流层折射误差和电离层折射误差;Nrs为载波相位的整周模糊度;λ为信号波长;c为光在真空中的传播速度;εr, Ps为伪距观测噪声和多路径效应误差之和;εr, Ls为载波相位观测噪声和多路径效应误差之和。
2 基于全球卫星导航系统接收机的信号稳定性分析方法全球卫星导航系统空间信号的稳定性分析一般通过评估监测接收机输出的伪距与载波相位的稳定性实现。全球卫星导航系统信号稳定性分为短期稳定性(1天或几小时)和长期稳定性(一星期)。信号短期稳定性主要受接收机短暂失锁和接收机时钟钟跳等因素的影响,这些因素导致载波相位和伪距观测值突然产生跳变,然后又恢复正常,而信号长期稳定性主要与卫星时钟有关,如卫星钟频率漂移导致载波相位和伪距观测量出现缓慢变化,致使两个观测量整体产生漂移,这种现象反映了信号的长期稳定性[9]。本节介绍全球卫星导航系统信号稳定性的分析方法,为评估载波相位和伪距测量值的稳定性,主要分析二者的曲线拟合残差。首先利用一段时长的载波相位或伪距测量值,对其进行多项式拟合,然后获得多项式拟合残差。多项式拟合依据最小二乘原理对原始观测数据进行拟合,使得原始观测数据和拟合曲线之间具有最小的差值。具体实现方法为,给定观测数据(xi, yi)(i=1, 2, …, m),寻找n阶多项式fn(x),使得拟合误差ri=yi -fn(xi)(i=1, 2, …, m)的平方和最小,即
| $ \mathit{E=}\sum\limits_{i=1}^{m}{{{\left[{{y}_{i}}={{f}_{n}}\left( {{x}_{i}} \right) \right]}^{2}}}=\sum\limits_{i=1}^{m}{{{\left[\sum\limits_{j=1}^{m}{{{a}_{j}}x_{i}^{j}-{{y}_{i}}} \right]}^{2}}=\min, } $ | (3) |
满足(3) 式的
根据多项式拟合残差的变化情况评估载波相位和伪距测量值的稳定性,基本步骤如下:
(1) 读取全球卫星导航系统监测接收机的原始观测数据,包括载波相位观测值和伪距观测值;
(2) 绘制载波相位观测值和伪距观测值曲线图,根据曲线图判断观测数据中是否存在跳变点;
(3) 截取一定时长的连续观测数据进行多项式拟合,获得多项式拟合残差;
(4) 根据多项式拟合残差的变化范围分析观测值的稳定情况。
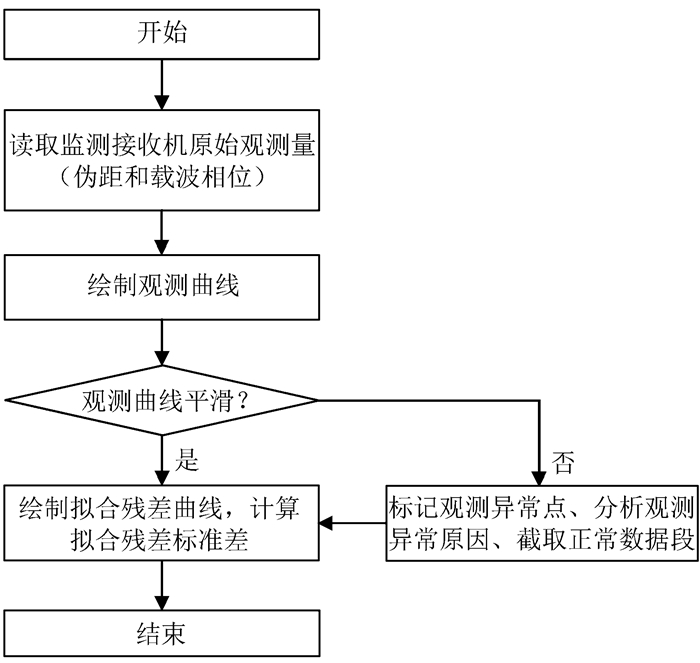
图 2为分析载波相位和伪距观测量稳定性的算法流程图。
|
| 图 2 基于全球卫星导航系统接收机的伪距和载波相位稳定性分析流程图 Figure 2 Flowchart of the method for analyzing the stability of pseudo-range and carrier-phase |
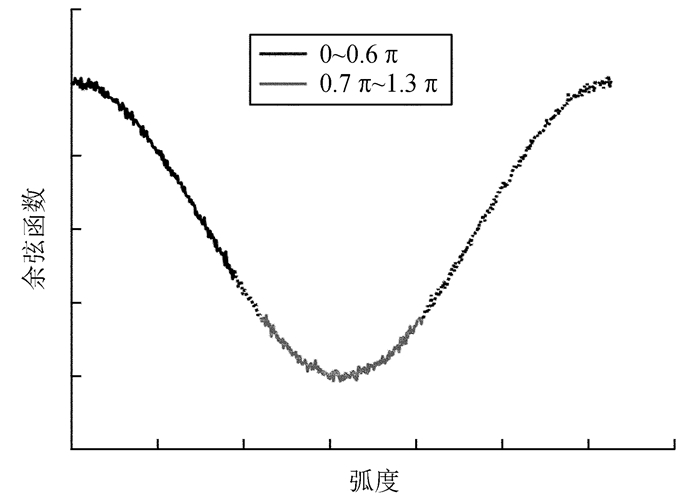
1天的原始伪距和载波相位观测数据的曲线图近似正弦或余弦函数(可以参见第4节给出的原始伪距测量曲线)。为不失一般性,首先产生一个周期(0~2 π)的叠加高斯白噪声的余弦函数以仿真伪距观测值,总共629个数据点,如图 3,然后分别截取0~0.6 π与0.7 π~1.3 π这两段模拟数据进行拟合,这两段数据均包含拐点。表 1列出了叠加不同高斯白噪声情况下的多项式拟合残差标准差,记为σ2,同时表 1也给出了未叠加高斯白噪声时的拟合残差标准差,记为σ1。
|
| 图 3 叠加高斯白噪声(标准差为0.020) 的余弦曲线 Figure 3 Cosine function with White Gaussian Noise (WGN) (σ=0.020) |
| 高斯白噪声标准差 | σ1 | σ2 | |||
| 0~0.6 π |
0.7~1.3 π |
0~0.6 π |
0.7~1.3 π |
||
| 0.020 | 0.001 | 0.002 | 0.024 | 0.020 | |
| 0.040 | 0.001 | 0.002 | 0.044 | 0.040 | |
| 0.050 | 0.001 | 0.002 | 0.053 | 0.050 | |
从表 1可以看到,对于未叠加高斯白噪声的数据拟合,多项式拟合残差标准差σ1均比较低,接近于0,这说明运用多项式拟合方法获得的拟合结果与原始观测值之间符合得较好。以未叠加高斯白噪声的多项式拟合残差标准差为参考,向余弦函数中加入标准差分别为0.020、0.040和0.050的高斯白噪声,获得了含噪数据与拟合数据之间的拟合残差标准差σ2。经过对比可以发现,σ2和高斯白噪声的标准差非常相近甚至相等,这进一步表明,多项式拟合方法对含噪数据的拟合结果与原始数据之间也具有很好的符合性,剩余的拟合残差一般是混杂在原始数据中的随机噪声成分。
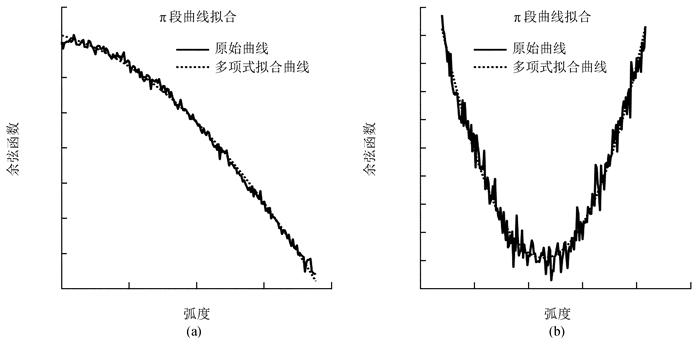
为更加直观地显示多项式拟合结果,图 4(a)和图 4(b)分别绘出了0~0.6 π与0.7 π~1.3 π两段含噪数据曲线和多项式拟合曲线之间的比较。从图 4可以看出,多项式拟合方法在图 4(a)和图 4(b)曲线拐点处的拟合效果不佳,但是总体而言,图 4(a)和图 4(b)曲线的整体拟合残差较小,拟合残差标准差与叠加的高斯白噪声的标准差非常接近,可见曲线拐点对多项式拟合效果影响不大,所以在曲线拐点处,多项式拟合仍然有效。
|
| 图 4 多项式拟合曲线与原始曲线对比 Figure 4 Comparison between the polynomial fitting and original time-series |
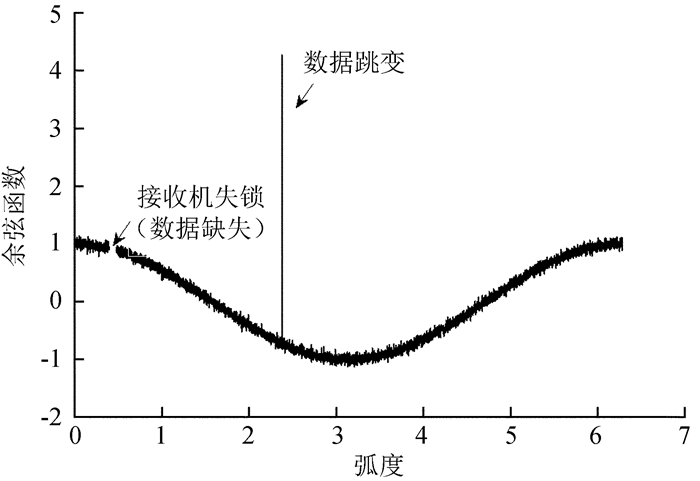
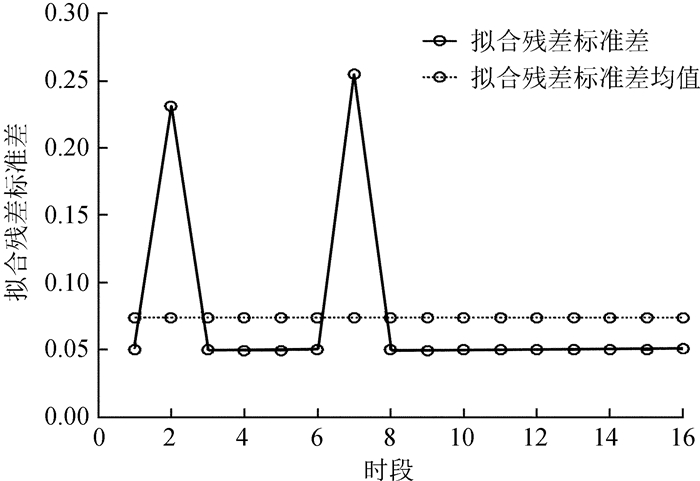
利用数字仿真分析观测数据异常条件下的多项式拟合效果,包括卫星时钟钟跳等导致的测量数据跳变、接收机失锁等因素造成的观测数据缺失。首先采用0~2 π一个周期的含噪余弦曲线仿真1天的载波相位或伪距观测数据,总共6 284个数据点。然后分别在0.13 π~0.15 π段和0.76 π点模拟接收机失锁等引起的数据缺失和卫星时钟钟跳等引起的数据跳变异常,其中数据缺失点为30个,如图 5。最后以392个数据为间隔将6 284个数据点分为16段,计算在不同噪声条件下每段数据的多项式拟合残差标准差,限于篇幅,图 6仅绘出了高斯白噪声标准差为0.050时的拟合残差标准差,表 2统计了两种观测异常情况下的拟合残差标准差与其均值之差。
|
| 图 5 观测数据异常仿真曲线(高斯白噪声标准差为0.050) Figure 5 Simulated observational anomaly with White Gaussian Noise (WGN) (σ=0.050) |
|
| 图 6 高斯白噪声标准差为0.050时的拟合残差标准差 Figure 6 Standard deviation of fitting residuals with White Gaussian Noise (WGN) (σ=0.050) |
| 高斯白噪声 标准差 |
拟合残差 标准差均值 |
差值 (数据缺失) |
差值 (数据跳变) |
| 0.020 | 0.048 | 0.176 | 0.205 |
| 0.040 | 0.065 | 0.161 | 0.188 |
| 0.050 | 0.074 | 0.154 | 0.184 |
从图 6和表 2可以发现,观测数据产生缺失和跳变异常现象时,多项式拟合残差标准差较大,这说明当载波相位或伪距出现观测异常时,基于多项式拟合的信号评估方法失效,因此必须截取正常的观测数据进行信号评估。
4 工程实例根据信号稳定性评估方法,对北斗系统G02地球同步轨道卫星B2频点Ⅰ支路2015年3月6日1天的伪距测量数据进行稳定性分析评估,监测接收机输出数据的采样间隔为30 s,连续记录2 880个观测值。
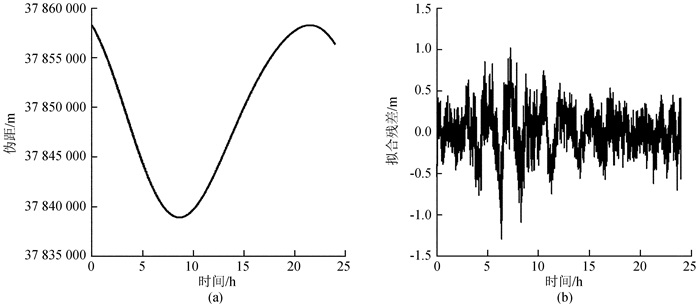
图 7(a)和图 7(b)分别绘出了00:00~24:00 24 h原始伪距观测值曲线及其多项式拟合残差曲线。由图 7(a)可以看出,该地球同步轨道卫星的伪距观测曲线平滑,没有发生数据缺失和数据跳变等异常。从图 7(b)可以发现,伪距多项式拟合残差曲线在0附近波动,并且在一定范围内变化。由图 7(b)还可以发现,相对而言,06:00~09:00时段的多项式拟合残差曲线不如其它时段的拟合残差曲线变化平稳。表 3列出了以3 h为一个时段划分的1天的伪距拟合残差标准差及其与标准差均值之差。从表 3可以看出, 除06:00~09:00时段外,其它时段的伪距拟合残差标准差相对于标准差均值之差的绝对值均小于0.100 m,06:00~09:00时段的标准差最大,为0.434 m,与标准差均值的偏差为0.183 m,与标准差均值差值最小的时段为12:00~15:00,其标准差为0.218 m,偏差值为-0.033 m。
|
| 图 7 伪距原始观测值及其多项式拟合残差 Figure 7 Original pseudo-range measurements and its polynomial fitting residuals |
| 时段 | 拟合残差标准差/m | 与标准差均值之差/m |
| 00:00~03:00 | 0.193 | -0.058 |
| 03:00~06:00 | 0.299 | 0.048 |
| 06:00~09:00 | 0.434 | 0.183 |
| 09:00~12:00 | 0.298 | 0.047 |
| 12:00~15:00 | 0.218 | -0.033 |
| 15:00~18:00 | 0.203 | -0.048 |
| 18:00~21:00 | 0.154 | -0.097 |
| 21:00~24:00 | 0.212 | -0.039 |
| 均值 | 0.251 | 0.000 |
06:00~09:00时段的伪距拟合残差相对于其它时段残差较大的原因在于,06:00~09:00时段的伪距观测值正好位于24 h伪距观测曲线的拐点处。曲线拐点位置的拟合效果一般没有其它时段的拟合效果好,但是曲线拐点处的拟合不会给整体数据的拟合结果带来影响,故多项式拟合结果是可信和可用的,这从表 3最后一行给出的标准差均值也可以看出,06:00~09:00时段的拟合没有影响整体数据的拟合结果,并且与3.2节观测异常的模拟结果相比,该时段的伪距拟合残差标准差要比伪距发生观测异常时的拟合残差标准差小很多。因而可以认为,06:00~09:00时段的拟合残差表现较大的现象与拟合时段划分有关,而不是由信号稳定性起伏引起的。
为了进一步分析06:00~09:00时段的伪距拟合残差结果,对残差统计特性进行讨论。多项式拟合残差主要包含混杂在原始数据中的随机噪声成分,换言之,伪距拟合残差通常是由观测噪声产生的随机波动,理论上应该服从零均值的高斯分布,然而由(1) 式可知,卫星信号在空间传播过程中受到对流层和电离层折射误差等多种因素的影响,从而导致总体方差和总体均值产生变化,若想知道总体方差和总体均值的变化情况,需要对两个高斯分布总体方差比或总体均值差进行估计。这里仅估计两个高斯分布总体均值差。
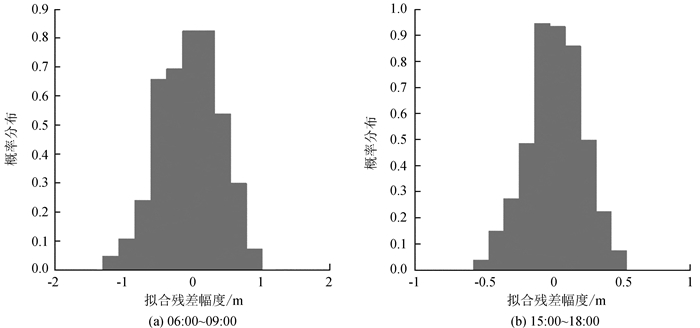
选取06:00~09:00和15:00~18:00两个时段的多项式拟合残差值(概率分布如图 8)作为两个总体(方差和均值等参数见表 4),估计两个总体均值差的一个置信度为1-α的置信区间[10],
|
| 图 8 伪距多项式拟合残差概率分布 Figure 8 Probability distribution of polynomial fitting residuals |
| 高斯总体 | 样本数 | 总体均值 | 总体方差 |
| 06:00~09:00 | n1=10 | μ1=0.040 | σ12=0.189 |
| 15:00~18:00 | n2=10 | μ2=0.021 | σ22=0.041 |
为了分析卫星导航信号的稳定性,以最小二乘拟合原理为基础,通过对监测接收机的载波相位和伪距测量数据进行评估,实现了对全球卫星导航系统空间信号稳定性的分析。数字仿真结果表明,多项式拟合方法在曲线拐点处的拟合效果不如曲线其它处,但曲线拐点处的拟合不会影响整体数据的拟合结果。当载波相位或伪距观测量因接收机失锁等因素出现数据缺失或因卫星时钟等因素引起数据跳变观测异常时,多项式拟合法不再适用,因而必须选取正常观测数据进行分析。通过对北斗系统地球同步轨道卫星伪距实测数据的评估可以发现,该卫星发射的Ⅰ支路信号在1天内是稳定的。由于多项式拟合方法具有一定的局限性,给信号评估结果带来一定的影响,因此如何对拟合方法进行改进是下一步的研究重点。此外,如何根据卫星信号的变化趋势进行信号的长期稳定性评估也是未来研究的关注点。
| [1] |
卢晓春, 周鸿伟. GNSS空间信号质量分析方法研究[J]. 中国科学:物理学力学天文学, 2010, 40(5): 528–533 Lu Xiaochun, Zhou Hongwei. Methods of analysis for GNSS signal quality[J]. Scientic Sinica:Physica, Mechanica & Astronomica, 2010, 40(5): 528–533. |
| [2] | Christie J R I, Bentley P B, Ciboci J W, et al. GPS signal quality monitoring system[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of the ION GNSS, 2004:2239-2245. |
| [3] | Spelat M, Hollreiser M, Crisci M, et al. GIOVE-A signal in space test activity at ESTEC[C]//Proceedings of the 19th International Technical Meeting of the Satellite Division of the ION GNSS, 2016:981-993. |
| [4] | 贺成艳. GNSS空间信号质量评估方法研究及测距性能影响分析[D]. 西安: 中国科学院国家授时中心, 2013. He Chengyan. Research on evaluation methods of GNSS signal quality and the influence of GNSS signal on ranging performance[D]. Xi'an:National Time Service Center, Chinese Academy of Science, 2013s. |
| [5] |
余宜珂, 王萌. 基于CAPS系统的信号调制方式的比较研究[J]. 天文研究与技术, 2014, 11(3): 224–229 Yu Yike, Wang Meng. Comparative studies of signal-modulation methods based on the CAPS[J]. Astronomical Research & Technology, 2014, 11(3): 224–229. |
| [6] | Soellner M, Kurzhals C, Hechenblaikner G, et al. GNSS offline signal quality assessment[C]//Proceedings of the 21st International Technical Meeting of the ION GNSS, 2008:909-920. |
| [7] |
石慧慧, 卢晓春, 饶永南. GNSS信号稳定性评估方法研究[J]. 时间频率学报, 2013, 36(2): 97–105 Shi Huihui, Lu Xiaochun, Rao Yongnan. Methods of evaluation for GNSS signal stability[J]. Journal of Time and Frequency, 2013, 36(2): 97–105. |
| [8] | Jin S G. Global Navigation Satellite Systems:signal, theory and applications[M]. Croatia: InTech Publisher, 2012: 4. |
| [9] |
康四林, 李语强. GPS定位中的误差分析[J]. 天文研究与技术——国家天文台台刊, 2010, 7(3): 222–230 Kang Silin, Li Yuqiang. Error analysis of GPS positioning[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2010, 7(3): 222–230. |
| [10] |
曾五一, 肖红叶. 统计学导论[M]. 北京: 科学出版社, 2007. Zeng Wuyi, Xiao Hongye. Introduction to statistics[M]. Beijing: Scientific Press, 2007. |


