引用本文
Jinghan Peng, 王娜. 土星主要卫星天体测量定标试验[J]. 天文研究与技术, 2017, 14(3): 322-329.  
Jinghan Peng, Wang Na. Astrometric Calibration of CCD Field of View for Some Major Satellites of Saturn[J]. Astronomical Research and Technology, 2017, 14(3): 322-329.  
土星主要卫星天体测量定标试验
Jinghan Peng1,2, 王娜2     
1. Department of Physics & Astronomy, University of British Columbia, Vancouver, BC V6T 1Z1, Canada;
2. 暨南大学天体测量、动力学与空间科学中法联合实验室, 广东 广州 510632
收稿日期: 2016-08-20; 修订日期: 2016-09-06
基金项目: 国家自然科学基金（U1431227）资助
作者简介: Jinghan Peng, 女, 学士.研究方向:天文资料处理.Email:jinghanpeng20@gmail.com
通讯作者: 王娜, 女, 博士.研究方向:天文图像处理, 天体测量. Email: twangna@jnu.edu.cn
摘要: 在地面望远镜观测土星主要卫星的精确定位中，目前普遍采用CCD成像技术。为了测量视场中暗卫星的位置，常采用4颗主要卫星（土卫三-土卫六）进行定标。鉴于技术的进步，目前CCD视场正在逐步增加，如何精确定标图像值得研究。利用2010年1月20日在云南天文台1m望远镜上观测的不同取向的105幅CCD图像进行了试验研究。采用了美国喷气推进实验室土星主要卫星历表和美国海军天文台的UCAC4恒星星表进行计算，相对于不同的参考对象进行定标。结果表明，采用4颗主要卫星进行定标并测量离卫星较近的观测对象时具有较好的测量准确度和内部精度。测量离定标星较远的卫星时，这种定标方法具有较大的不确定性。采用6颗主要卫星（土卫三-土卫八）进行定标，所有卫星的测量结果具有更好的外部和内部符合。即便如此，采用四常数模型和六常数模型定标的结果都不是令人满意，这揭示CCD视场存在明显的扭曲效应。如果采用视场中的恒星定标，卫星的外部符合和内部精度明显变差，这说明UCAC4恒星参考星表也不是理想的定标用参考星表。
关键词: 天体测量     几何定标     土星卫星    
Astrometric Calibration of CCD Field of View for Some Major Satellites of Saturn
Jinghan Peng1,2, Wang Na2     
1. Department of Physics & Astronomy, University of British Columbia, Vancouver, BC V6T 1Z1, Canada;
2. Sino-France Joint Laboratory for Astrometry, Dynamics and Space Science, Jinan University, Guangzhou 510632, China
Received date: 08-20-2016; Received in revised form 09-06-2016
Corresponding author: Wang Na, Email: twangna@jnu.edu.cn.
Abstract: CCD imaging has been used to derive their precise positions of Saturnian major satellites during past two decades. In order to obtain the positions of some faint satellites near to their primary planet, the four bright satellites Tethys, Dione, Rhea and Titan are often used to calibrate their CCD field of view. Due to continuous progress in technology, recent CCD field of view becomes greater and greater, thus precise calibration of the CCD field of views deserves to study deeply. Experimental tests have been done based on 105 CCD frames with different orientations for Saturnian major satellites taken by the 1-m telescope at Yunnan Observatory on Jan. 20, 2010. The JPL ephemeris of Saturnian satellites is used for the major satellites and the star catalogue UCAC4 is used for the stars appearing in the CCD field. Different calibrated objects are chosen to calibrate the CCD field of view. Our tests show that when the four bright satellites (Tethys, Dione, Rhea and Titan) are used, a satellite near to the four satellites can be determined precisely, this confirms the former practice. However, for a wide separated satellite it will have great uncertainty. If the six major satellites (Tethys, Dione, Rhea, Titan, Hyperion and Iapetus) appearing in the same field are used to calibrate, all satellites will have better outer and inner agreements. Anyway, the distortion has shown its existance in the CCD field of view. Besides, if only the faint stars (in UCAC4) appearing in the same field are used to calibrate, the agreement in both inner and outer will become worse obviously. This experiment has shown that the UCAC4 catalogue is not precise enough to calibrate the CCD field of view.
Key words: Astrometry     Geometric calibration     Saturnian satellites    

土星的卫星系统类似一个小的太阳系，研究系统位置的变化和演化规律，对土卫系统和太阳系的演化均具有重要意义。虽然有空间观测(如哈勃空间望远镜[1]和Cassini成像观测[2])的高精度观测结果，地面望远镜长期观测仍然是不可替代的重要方式。地面望远镜观测土星主要卫星的精确定位中，有两种主要方法：(1) 观测卫星之间的互掩互食光变曲线并由此提取高精度的天体测量信息，这是一种精度非常高的观测方式[3]，但这种观测方式需要大约12年才有观测机会；(2) 最为常用的观测方式是采用长焦距望远镜CCD成像观测。CCD应用于天文观测以来，采用这种观测方式获得了大量的观测资料[4]。

地面长焦距望远镜CCD观测土星主要卫星的位置时，难点之一是高精度的位置定标。人们曾研究过多种定标方法，但目前比较普遍的定标方法是采用土星的4颗主要卫星的理论位置和观测的像素位置进行比较求解定标参数[5-7]。例如，文[5]直接采用CCD图像中土卫三-土卫六这4颗卫星的理论位置和像素位置进行比较求解图像的比例尺和取向。文[6]采用同样的方法评价了当代的4个土卫理论，并发现土星卫星的分析理论(Théorie Anlytique des Satellites de Saturne, TASS)具有明显的优越性，建议今后可以使用该理论进行定标。文[7]采用TASS理论中的土卫三-土卫六进行定标，发表了2002~2006年观测的359帧图像中共计2 154个土卫一-土卫六的精确位置。

因为CCD视场通常较小(例如约5′)，人们理所当然地认为它是理想的，四常数模型是足够的。由于卫星之间的相对位置测量可以用于历表的开发[8-9]，只需两个定标参数(比例尺和取向)即可以测量土星卫星的相对位置。然而，这种定标方法有不足之处。一方面，虽然4颗主要卫星的理论位置通常相对高精度，但逻辑上，这种位置测量并非令人满意，文[10]对此持有批评的态度。另一方面，CCD视场的特性往往不清楚，四常数模型的描述没有充分证明，短期的观测往往很难发现视场的几何特性的不均匀性。这是因为短期观测时，卫星在CCD视场的位置往往变化很小，位置观测残差的内部符合表面上是高精度的。

文[11]通过将安装CCD芯片的底座旋转90°，观测疏散星团发现原来常用的四常数模型非常不精确，需要高达30个常数模型才能精确描述CCD视场的几何特性。文[12]开发了一种新方法求解CCD图像的几何扭曲。

本文继续这一研究工作，在云南天文台1 m望远镜上对土星主要卫星进行了CCD观测。将安装CCD芯片的底座旋转了3个不同的方向：30°、-60°和0°分别对土星主要卫星和视场中的部分暗恒星成像，试图研究土星主要卫星的位置测量残差随定标用参考对象、参考对象的个数等的变化规律，并给出具体的数值大小。根据前面的描述，因为采用不同的取向进行观测，同一卫星成像于CCD中不同的位置，相同卫星的位置残差容易反映定标的优劣，因为合适的定标必将得到相同的位置残差。

本文第1部分描述了获取的观测资料及图像处理，第2部分介绍了数据归算方法，第3部分讨论处理的结果，最后是结论。

1 观测资料与图像处理

2010年1月20日，在云南天文台1 m望远镜上进行了土星卫星的CCD定位观测。观测过程中使用I滤光片，并将安装CCD芯片的底座在3个不同方向进行观测。具体地，这3个不同方向对应于CCD图像的取向(大约)分别为30°、-60°和0°。这里方向定义为CCD图像的水平轴与赤纬圈的夹角。这样观测的目的是研究观测的目标星残差随方向的变化情况，如果CCD视场精准定标，那么这一残差将保持不变。使用的1 m望远镜和CCD的参数见表 1。

表 1 使用的望远镜和CCD参数 Table 1 The telescope used and CCD parameters
近似焦距
/m		 焦比
(F数)		 主镜直径
/cm		 CCD
视场大小		 像素大小
/μ		 图像
分辨率		 像素近似比例尺
/pixel
13.3 13 100 7′.1 × 7.′1 13.5 × 13.5 2 048 × 2 048 0.″21
表选项

在上述3个方向观测的图像帧数分别为30、30和45。每幅图像的曝光时间为8~12 s，具体依赖于天气状况。此时，主星土星通常过度饱和以确保暗卫星(如土卫七)具有良好的信噪比。图 1给出了3种不同方向观测时的典型CCD图像。

图 1 3个不同方向(从左到右分别约30°、-60°和0°)观测的土星卫星典型图像。图中给出了土卫三(Tethys)、土卫四(Dione)、土卫五(Rhea)、土卫六(Titan)、土卫七(Hyperion)和土卫八(Iapetus)。此外还标注了一颗离土卫四和土卫六较近的恒星(Star0) Figure 1 Typical CCD frames in different orientations (30, -60 and 0 deg from left to right). Among the frames, Tethys, Dione, Rhea, Titan, Hyperion and Iapetus are tagged. In addition, two stars are also shown)
图选项

为了测量卫星和若干恒星(每个视场3颗暗恒星)的像素位置，采用两种不同的方案。如果观测对象离土星较远(如土卫六、土卫七、土卫八以及若干恒星)，采用一阶背景叠加二维高斯函数的方法进行拟合，求解像素位置，如果观测对象离土星较近，采用二阶背景叠加二维高斯函数的方法进行拟合，求得像素位置，而土星本体由于过度饱和不做测量。

2 归算方法

自CCD用于土卫定位观测以来，采用土卫三-土卫六的量度坐标(即像素坐标)和理论位置的比较并采用四常数模型进行定标，以便测量暗的土星卫星和其他卫星的位置。这种定标方法有其局限性，并不令人满意。

鉴于目前土星卫星空间观测的进展和理论研究的成果，也因为CCD图像的视场逐步增大，需要深入分析CCD视场的特性。

具体地可以采用下面几种情况对图像进行定标：(1) 参考土卫三-土卫六进行定标，研究离它们较近的观测目标的定位精度，包括定标星本身的定位精度。这里采用简单的四常数模型。(2) 鉴于目前土卫三-土卫八具有良好的理论位置[2]，可以参考所有这些卫星进行定标，采用四常数或六常数模型。(3) 采用视场中为数极少(3颗)的暗恒星进行定标，用四常数模型求解所有卫星的位置。

3 结果与讨论

分3种情况进行图像的定标。

(1) 参考土卫三-土卫六，并采用四常数模型进行定标。

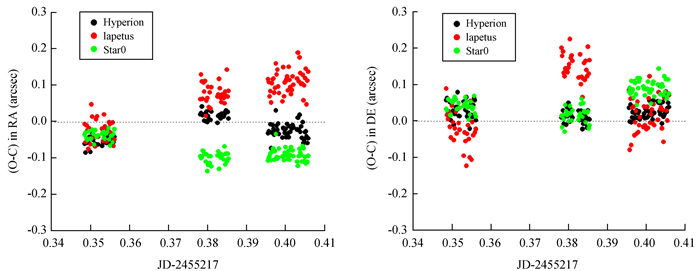
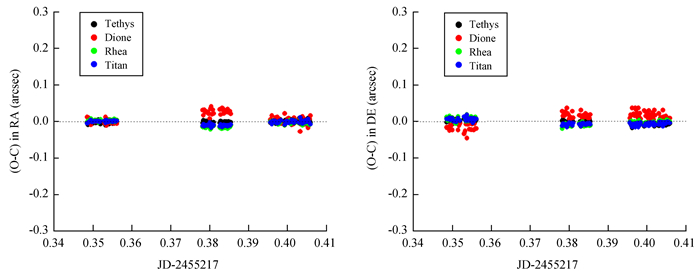
表 2、图 2和图 3给出观测的所有卫星及在3个不同方向中出现的一颗共同星(UCAC编号为453-053377) 的位置测量结果，其中，(O-C)表示观测的位置(Observed)减去计算位置(Computed)，即残差。这里计算位置采用了喷气推进实验室历表(http://ssd.jpl.nasa.gov)的站心视位置，并考虑大气折射的影响。由表 2、图 2可见，土星主要卫星土卫三-土卫六具有良好的内部符合(最大平均残差的绝对值在两个方向均不超过0.01″)，而且位置测量的内部精度(标准差)均优于0.02″，尤其对于土卫三、土卫五和土卫六。

表 2 参考土卫三-土卫六并采用四常数模型定标，测量所有卫星和恒星Star0的位置(单位：角秒) Table 2 A 4-constant plate model derived by Tethys, Dione, Rhea and Titan, and the measured positions of all satellites and the star0 are listed
观测对象 资料数 赤经平均残差 标准差 赤纬平均残差 标准差
Tethys 105 -0.001 0.004 -0.003 0.006
Dione 105 +0.009 0.014 +0.008 0.017
Rhea 105 -0.005 0.007 -0.002 0.008
Titan 105 -0.003 0.006 -0.003 0.007
Hyperion 105 -0.021 0.031 +0.023 0.021
Iapetus 105 +0.062 0.063 +0.047 0.080
Star0 105 -0.078 0.030 +0.054 0.037
表选项
图 2 参考土卫三-土卫六，以四常数模型定标，测量土卫三-土卫六的位置残差 Figure 2 A 4-constant plate model with respect to Tethys, Dione, Rhea and Titan and their positional residuas
图选项
图 3 参考土卫三-土卫六，以四常数模型定标，测量土卫七、土卫八和共同恒星的位置残差 Figure 3 Positional residuals of Hyperion, Iapetus and a common star derived by the 4-constant plate model as in Fig. 2
图选项

另一方面，从表 2和图 3可知，对于土卫七的观测，其位置测量精度(标准差)为0.02~0.03″，明显低于土卫三-土卫六。这可以解释为其亮度较低，具有较低的信噪比所致。然而，对于土卫八，无论是外部符合还是内部精度都明显低于土卫七。因为土卫八明显亮于土卫七，信噪比高于土卫七，不能解释为信噪比低的缘故。问题在于这颗卫星离定标的土卫三-土卫六较远(见图 1)，因此，定标参数的误差起到放大作用。无论如何，这一试验验证了确实可以采用土卫三-土卫六定标，对近距离的目标具有较好的精确度和准确度，但对较远的卫星则具有明显的误差。

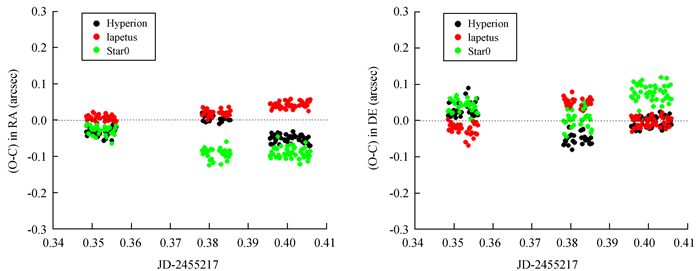
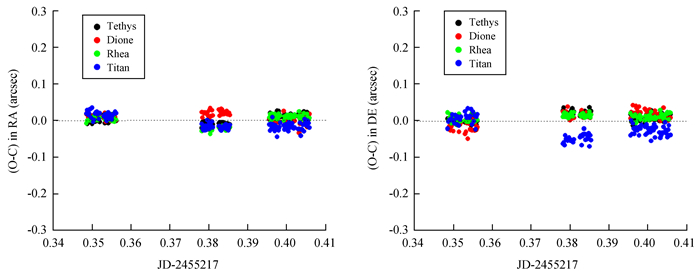
(2) 参考所有卫星土卫三-土卫八进行定标，并分四常数模型和六常数模型进行试验。由表 3、图 4、图 5可见，与表 2、图 2、图 3结果相比，土卫三-土卫六的测量结果没有明显的变化(仅土卫六在赤纬方向的平均残差有约0.02″的变化)，但土卫七和土卫八具有较大的变化，尤其是土卫八，其位置精度(在赤经方向的标准差)明显好于土卫七，这反应定标方案更接近实际情况。至于暗恒星的测量结果，它与表 2中的情况类似，变化不大。

表 3 参考土卫三-土卫八并采用四常数模型定标，测量所有卫星和恒星Star0的位置(单位：角秒) Table 3 A 4-constant plate model with respect to 6 satellites from Tethys to Iapetus, and positional for all satellites and the star 0 are listed
观测对象 资料数 赤经平均残差 标准差 赤纬平均残差 标准差
Tethys 105 +0.003 0.011 +0.008 0.011
Dione 105 +0.009 0.011 +0.007 0.018
Rhea 105 -0.000 0.014 +0.009 0.009
Titan 105 -0.007 0.017 -0.024 0.024
Hyperion 105 -0.030 0.026 -0.006 0.036
Iapetus 105 +0.025 0.018 +0.006 0.032
Star0 105 -0.073 0.031 +0.046 0.037
表选项
图 4 参考土卫三-土卫八，以四常数模型定标，测量土卫三-土卫六的位置残差 Figure 4 A 4-constant plate model derived by 6 satellites (Tethys, Dione, Rhea, Titan, Hyperion and Iapetus) and positional residuals of Tethys, Dione, Rhea and Titan are shown
图选项
图 5 参考土卫三-土卫八，以四常数模型定标，测量土卫七、土卫八和共同恒星的位置残差 Figure 5 The same plate model as in Fig. 4 and positional residuals of Hyperion and Iapetus are shown
图选项

总之，上面两种情况，验证了采用四常数模型进行定标的近似正确性。

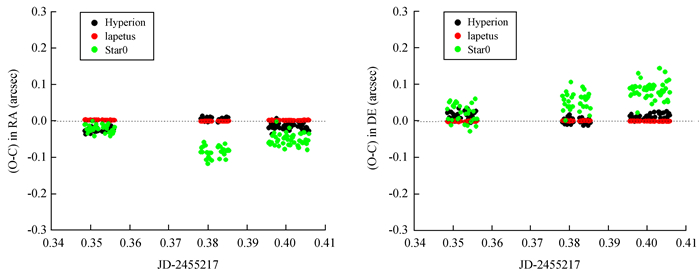
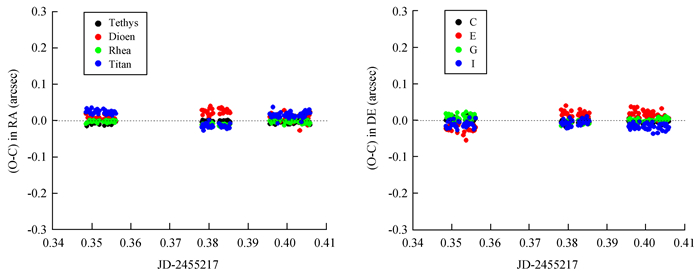
表 4、图 6、图 7显示了参考土卫三-土卫八并采用六常数模型定标的结果。分别与表 3、图 4、图 5相比，土卫三-土卫六和恒星的测量结果变化不大。最大的变化是土卫七和土卫八，尤其是土卫八。其外部符合和测量精度有了显著提高，达到了1 mas准确度和精度。这可能更加反应了真实的情况，因为土卫八较亮，其位置测量精度本应该较高。此外，土卫七的外部符合(平均残差)在赤经方向有了明显变化，位置测量精度也显著提高，达到了内部符合约10 mas的精度。土卫七和土卫八位置测量结果的改善，说明了六常数模型相比四常数模型更符合实际情况, 也说明了CCD视场并非理想。近距离的暗恒星Star0，在3种方向条件下都具有明显不同的平均残差(见图 7)，揭示了视场存在明显的扭曲效应。

表 4 参考土卫三-土卫八并采用六常数模型定标，测量所有卫星和恒星Star0的位置(单位：角秒) Table 4 A 6-constant plate model derived by the 6 satellites from Tethys to Iapetus, positional measurement of all satellites and the star0 are given
观测对象 资料数 赤经平均残差 标准差 赤纬平均残差 标准差
Tethys 105 -0.004 0.004 -0.002 0.007
Dione 105 +0.012 0.012 +0.006 0.018
Rhea 105 -0.005 0.006 +0.000 0.008
Titan 105 +0.009 0.017 -0.012 0.009
Hyperion 105 -0.012 0.013 +0.008 0.010
Iapetus 105 +0.001 0.001 -0.001 0.001
Star0 105 -0.051 0.028 +0.058 0.035
表选项
图 6 参考土卫三-土卫八，以六常数模型定标，测量土卫三-土卫六的位置残差 Figure 6 A 6-constant plate model by the 6 satellites from Tethys to Iapetus, and positional residuals of Tethys, Dione, Rhea and Tita are shown
图选项
图 7 参考土卫三-土卫八，以六常数模型定标，测量土卫七、土卫八和共同恒星的位置残差 Figure 7 A 6-constant plate model derived by the 6 satellites as in Fig. 6, and the positional residuals for Hyperion, Iapetus and the common stars are shown
图选项

(3) 参考每一方向情况下的3颗恒星进行定标(不同方向下的3颗恒星不完全相同)，并采用四常数模型进行试验。

理论上，使用恒星进行定标，测量同一视场的所有卫星的位置是最理想的。但目前仍然有两方面的困难。一方面，与土星卫星理论位置的精度相比，恒星的星表位置精度过低。例如UCAC4星表[13]的恒星精度在亮星部分约20 mas，何况自行的误差使得实际使用时，真实的位置精度更加难满足高精度测量土星卫星位置的要求。另一方面，CCD视场并非理想，为数极少的恒星难以完整描述CCD视场的几何特性。

从表 5可见，所有卫星的平均残差明显变大，而且位置测量的内部精度也显著增大。可能的解释是由不同的恒星进行定标，而它们的位置误差各不相同造成的。显然，不同恒星具有较大的位置误差，其结果精度不能与卫星直接定标的结果相比。唯一改善的是共同的恒星Star0，它的平均残差和前几种情况相比有明显减少。

表 5 参考每一方向下的恒星和四常数模型进行定标，测量所有卫星和恒星Star0的位置(单位：角秒) Table 5 A 4-constant plate model is derived from all 3 stars in 4 different orientations, positional residuals for all satellites and star0 are given
观测对象 资料数 赤经平均残差 标准差 赤纬平均残差 标准差
Tethys 105 +0.123 0.062 -0.039 0.032
Dione 105 +0.108 0.047 -0.022 0.028
Rhea 105 +0.121 0.069 -0.042 0.031
Titan 105 +0.057 0.050 -0.023 0.050
Hyperion 105 +0.021 0.026 +0.014 0.057
Iapetus 105 +0.080 0.060 +0.097 0.119
Star0 105 +0.006 0.074 +0.014 0.021
表选项

无论如何对于试验观测，恒星的位置误差过大，难以胜任精确定标。期望不久将开放的第1版的Gaia星表(http://iaus330.scienceconf.org/)，可以获得高精度的星表位置。

4 结论

利用云南天文台1 m望远镜在不同方向观测土星主要卫星的CCD图像。当采用主要卫星土卫三-土卫六进行定标时，离它们较近的观测目标具有较好的位置测量精度，而离这些参考卫星较远的观测目标，位置测量具有更大的不确定性。试验进一步表明，目前采用土卫三-土卫八能更好定标CCD图像。无论如何，采用四常数模型和六常数模型定标的结果都不令人满意，这反映了CCD视场存在明显的扭曲效应。目前的UCAC4星表不适合土卫的高精度定标。期望新的Gaia星表的释放，对于土卫高精度的定标将具有推动作用。但是，CCD图像扭曲的精确测定仍然是必须的。

致谢:

本文的观测资料得到了云南天文台1 m望远镜运行组的长期关心和支持，在此表示感谢。

参考文献
[1] French R G, McGhee C A, Frey M, et al. Astrometry of Saturn's satellites from the Hubble Space Telescope WFPC2[J]. The Publications of the Astronomical Society of the Pacific, 2006, 118(840): 246–259. DOI: 10.1086/pasp.2006.118.issue-840
[2] Tajeddine R, Lainey V, Cooper N J, et al. Cassini ISS astrometry of the Saturnian satellites:Tethys, Dione, Rhea, Iapetus and Phoebe 2004-2012[J]. Astronomy & Astrophysics, 2015, 575(3): 309–314.
[3] Arlot J E, Emelyanov N V, Lainey V, et al. Astrometric results of observations of mutual occultations and eclipses of the Saturnian satellites in 2009[J]. Astronomy & Astrophysics, 2012, 544: A29.
[4] Beurle K, Harper D, Jones D H P, et al. Preliminary analysis of CCD observations of Saturn's satellites[J]. Astronomy & Astrophysics, 1993, 269(24): 564–567.
[5] Vienne A, Thuillot W, Veiga C H, et al. Saturnian satellite observations made in Brazil during the 1995 opposition with an astrometric analysis[J]. Astronomy & Astrophysics, 2001, 380(2): 727–733.
[6] Shen K X, Dourneau G, Qiao R C, et al. An analysis of satellite calibration methods for CCD astrometry of Saturn's satellites[J]. Astronomy & Astrophysics, 2001, 367(367): 1061–1069.
[7] Peng Q Y, Vienne A, Wu X P, et al. CCD positions of Saturn and its major satellites from 2002-2006[J]. The Astronomical Journal, 2008, 136(5): 2214–2221. DOI: 10.1088/0004-6256/136/5/2214
[8] Sinclair A T. A theory of the motion of Iapetus[J]. Monthly Notices of the Royal Astronomical Society, 1974, 169(3): 591–605. DOI: 10.1093/mnras/169.3.591
[9] Sinclair A T. The orbits of Tethys, Dione, Rhea, Titan and Iapetus[J]. Monthly Notices of the Royal Astronomical Society, 1977, 180(180): 447–459.
[10] Lainey V, Karatekin O, Desmars J, et al. Strong tidal dissipation in Saturn and constraints on Enceladus' thermal state from astrometry[J]. The Astrophysical Journal, 2012, 752(1): 14. DOI: 10.1088/0004-637X/752/1/14
[11] Peng Q Y, Fan L Y. Accurate determination of the plate model based on CCD images with different orientations[J]. Chinese Science Bulletin, 2010, 55(9): 791–796. DOI: 10.1007/s11434-010-0053-2
[12] Peng Q Y, Vienne A, Zhang Q F, et al. A convenient solution to geometric distortion and its application to Phoebe's observations[J]. The Astronomical Journal, 2012, 144(6): 170–180. DOI: 10.1088/0004-6256/144/6/170
[13] Zacharias N, Finch C, Girard T, et al. The fourth US Naval Observatory CCD astrograph catalog[J]. The Astronomical Journal, 2012, 145(2): 531–544.
由中国科学院国家天文台主办。
0

文章信息

Jinghan Peng, 王娜
Jinghan Peng, Wang Na
土星主要卫星天体测量定标试验
Astrometric Calibration of CCD Field of View for Some Major Satellites of Saturn
天文研究与技术, 2017, 14(3): 322-329.
Astronomical Research and Technology, 2017, 14(3): 322-329.
收稿日期: 2016-08-20
修订日期: 2016-09-06

工作空间