射频干扰是射电天文中一个十分重要的问题。大部分的射电源信号属于微弱信号，需要长时间的积分才能够被接收机检测。由于低质量的滤波器泄露和邻近频带的互调干扰，射电天文观测数据总受到来自被国际电信联盟(International Telecommunication Union, ITU)保护的频带内的无线电信号的干扰。另一方面，根据可观测灵敏度与带宽之间的关系可知，最小灵敏度与带宽成反比，即采用更宽的输入带宽能够获得更微弱信号的探测能力。那么和目前日益增长的无线电频率使用必然形成矛盾，人工产生的比如卫星传输信号、雷达信号、无线通信信号和电视广播信号等大大强于射电天文信号(太阳射电爆发信号除外)，如果在观测频段内，会造成接收机饱和、假谱、交调干扰等一系列问题，影响天文观测的数据质量。

近几年来，一系列自适应波束形成算法已经成功应用于空间干扰消除^[1-2]，但是仍然有很多应用场景和信号环境是目前的方法不能应对的。当干扰移动相对较快时，传统的自适应干扰消除方法性能下降。本文方法基于已被广泛应用的子空间投影算法^[3-8]，主要考虑到它良好的零陷深度。子空间投影算法是通过阵列协方差矩阵的特征值分解得到干扰子空间的估计，继而将接收信号投影到干扰子空间的正交空间，以实现干扰消除。

虽然本文所提方法和原理通常适用于大范围的传感器阵列和自适应阵列的干扰消除，但在这里着重强调射电天文中的相控阵天线(Phased Array Feeds, PAFs)。这个应用对干扰移动相对于阵列协方差矩阵的估计时间间隔而言是相对快速的问题，是一个恰当的处理方法。采样时间间隔通常被称为短时积分窗(Short-term integration, STI)。

相控阵天线提供了一种有前途的新方法以利用干扰信号的空间结构跟踪和消除射频干扰而不会丢失任何有用数据^[8]。对于空间干扰消除而言，上述方法甚至可以消除完全遮盖有用信号的频谱的干扰源的影响。

本文第1节给出了信号模型的数学表示；第2节介绍了子空间投影的波束形成的详细原理和由于干扰源的相对移动导致的估计误差是如何限制零陷深度的；第3节提出了一种适用于移动干扰源的基于矩阵多项式模型的时变阵列协方差矩阵，以改善传统的子空间投影算法；第4节给出了仿真性能分析，由结果可知本文方法的干扰消除性能优于传统的子空间投影方法。

1 信号模型

假设x[n]是P × 1阶的阵列天线的复采样序列，它可以表示为

$ x\left[n \right]={{a}_{s}}s\left[n \right]+{{a}_{d}}\left[n \right]d\left[n \right]+\eta \left[n \right], $

(1)

其中，s[n]为观测的射电天文信号；a_s为s[n]阵列响应矢量；d[n]为干扰源信号；a_d[n]为d[n]阵列响应矢量。天线是固定跟踪观测源以保持射电源在视轴线上，因此a_s是常量。随着干扰源的相对运动或者天线跟踪射电源，a_d[n]随时间改变。噪声矢量η[n]假设为空域白高斯噪声。信号s[n]、d[n]和η[n]假设为广义宽平稳的高斯随机过程。那么，阵列协方差矩阵表示为

$ \begin{align} & {{R}_{x}}\left[ n \right]=E\left\{ \left. x\left[ n \right]{{x}^{H}}\left[ n \right] \right\} \right.=\sigma _{s}^{2}{{a}_{s}}a_{s}^{H}+\sigma _{d}^{2}{{a}_{d}}\left[ n \right]a_{d}^{H}\left[ n \right]+{{R}_{\eta }} \\ & \ \ \ \ \ \ \ \ \ ={{R}_{s}}+{{R}_{d}}\left[ n \right]+{{R}_{\eta }}, \\ \end{align} $

(2)

其中，R_x[n]的时间依赖性来自由移动干扰源产生的阵列响应矢量的变化，因此在一个短时积分窗内，它只能近似看做是广义平稳的。这个假设在干扰源移动速率相对于短时积分窗宽度较快时会失效。其他的所有信号假设为广义平稳的。

虽然R_x[n]随n连续变化，它只有假设在第k个短时积分间隔内是平稳的，因此可以得到它的L长度采样的估计值：

$ {{{\mathit{\hat{R}}}}_{\mathit{x, k}}}=\frac{1}{L}\sum\limits_{n=kL}^{\left( k+1 \right)L-1}{x\left[n \right]{{x}^{H}}\left[n \right]=}\frac{1}{L}{{X}_{k}}X_{k}^{H}, $

(3)

其中，X_k=[x[kL], …, x[(k+1)L-1]]为第k个短时积分窗L长度的采样数据。

2 传统的干扰消除算法 2.1 子空间投影干扰消除

在满足窄带的条件下，波束形成器的输出信号可以表示为

$ y\left[n \right]={{w}^{H}}x\left[n \right], $

(4)

其中，w为波束形成器的权矢量，以提供期望信号来向上的响应方向图。如果干扰信号相对于信号在阵列间的传播时间是时域宽带的，那么x[n]可以被分解为多个子带，每一个有各自的波束形成权矢量。

在传统的自适应波束形成算法中有很多可以用来设计w以得到期望的方向图主瓣、控制方向图形状和在干扰信号的方向上获得零点^[1-2]。

考虑到子空间投影算法可以得到更深的零陷深度，本文方法基于子空间投影算法实现^[6-8]。当干扰信号的强度大到可以主导R_x[n]中的噪声和有用信号时，波束形成权矢量可以用下面的方法计算：

$ \begin{matrix} {{w}_{\rm{SP, }\mathit{k}}}=P_{d, k}^{\bot }w \\ P_{d, k}^{\bot }=I-{{U}_{d, k}}U_{d, k}^{H} \\ \end{matrix}, $

(5)

其中，k为短时积分窗的索引值；P_{d, k}^⊥为估计的干扰子空间的正交投影矩阵；U_{d, k}包含了协方差矩阵分解中干扰信号对应的单位长度归一化的主特征向量：

$ {{\mathit{\hat R}}_{\mathit{x, k}}}\left[{{U_{d, k}}|{U_{s, \eta, k}}} \right] = \left[{{U_{d, k}}|{U_{s, \eta, k}}} \right]{\rm{\Lambda }}{\rm{.}} $

(6)

权值矢量w用来建立无干扰情况下的静态天线方向图。投影算子P_{d, k}^⊥w可能扰乱或者损坏期望的静态方向图，因此需要保证干扰从天线方向图的旁瓣进入。另一方面，U_{d, k}的秩必须小于天线个数P或有充分的自由度形成远离空域零点的期望的静态方向图。

在移动干扰源的应用场景中，w_{SP, k}在每一个新的L长度的采样中被重新计算以保持干扰消除零点在干扰来向上。在多干扰源的应用场景中，必须事先计算干扰个数m，而此时的干扰信号矩阵U_{d, k}的阶数为P × m。本文方法着重应用于单个干扰的情况，此时U_{d, k}是一个列矢量。

2.2 影响干扰消除性能的因素

提高采样数可以减小协方差矩阵$ {{\mathit{\hat R}}_{\mathit{x, y}}}$的采样估计误差，那么干扰子空间的估计精度和干扰消除算法的性能会随之提高。但当传统的子空间投影的波束形成抗干扰方法应用于移动干扰源的场景时，如果干扰移动速度过快而采样间隔过长，会引起阵列相应的不一致，造成阵列协方差矩阵的秩不等于干扰源数量即子空间扩散，那么自适应波束形成抗干扰算法将无法使用。因此分析采样估计误差和子空间扩散对传统自适应波束形成干扰消除算法的影响，为改进传统的自适应波束形成干扰消除算法做准备。

(1) 采样估计误差：在平稳信号环境中$ {{\mathit{\hat R}}_{\mathit{x, y}}}$是R_x[n]|_n=kL的一致估计，估计误差的方差减少了$ \frac{1}{L}$^[9]。为了减少估计误差，短时积分窗的长度应该尽可能长。

(2) 子空间扩散：$ {{\mathit{\hat R}}_{\mathit{x, y}}}$包含了第k个采样时间间隔的L长采样的时变R_d[n]的时间平均。尽管R_d[n]=σ_d²a_d[n]a_d^H[n]的秩为1，但采样间隔过长时，对移动干扰源做时间平均产生一个秩更高的矩阵，这就需要用更多的特征矢量去张成干扰子空间。只有当采样间隔的宽度相对于干扰移动速率较窄时，投影算子P才能有效地投影这个秩数较高的干扰分量。这个有限窗口的估计带来的影响通常叫做“子空间扩散”。

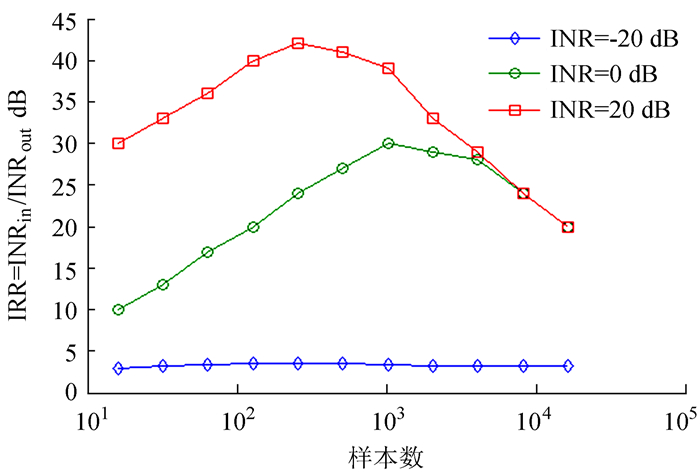
通过子空间投影波束形成抗干扰算法仿真得到的在不同输入干噪比情况下单移动干扰消除的干扰抑制比(Interference Rejection Ratio, IRR)如图 1。

从图 1可以看到，对于一个给定长度的样本数，一个更高的输入干噪比会带来更高的干扰抑制比，因为此时$ {{\mathit{\hat R}}_{\mathit{x, y}}}$的主特征向量更接近真实的干扰信号。同时，干扰抑制比随着样本数长度的增加而增加，直到子空间扩散开始影响干扰消除性能，这会产生一个干扰抑制比的最大值。随着样本数的继续增加，干扰消除性能开始急剧恶化，也就是说干扰源的移动限制了可得到的干扰抑制比的最大值。但是在较低输入干噪比的情况下，由于无法得到干扰子空间的准确估计，因此无法对干扰进行很好的消除，所以干扰抑制比并没有明显的变化。

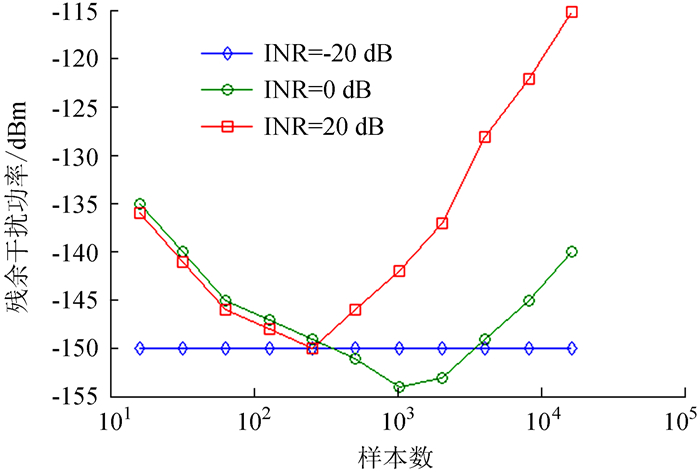
通过子空间投影波束形成抗干扰算法仿真得到在不同输入干噪比情况下单移动干扰消除残余干扰功率如图 2。

从图 2可以看到，对于一个给定长度的样本数，一个更高的输入干噪比带来更低的残余干扰，因为此时$ {{\mathit{\hat R}}_{\mathit{x, y}}}$的主特征向量更接近真实的干扰信号。同时，残余干扰功率随着样本数长度的增加而减小，直到子空间扩散开始影响干扰消除性能，这会产生一个残余干扰功率的最小值。随着样本数的增加，干扰消除性能开始急剧恶化，也就是说干扰源的移动限制了可得到的残余干扰功率的最小值。但是在较低输入干噪比的情况下，由于无法得到干扰子空间的准确估计，因此无法对干扰进行很好的消除。不过由于输入的干噪比很低，所以此时的残余干扰功率也很低。

3 基于多项式模型的子空间投影

由上述分析可知，传统的自适应波束形成抗干扰方法在样本数有限的情况下，由于协方差矩阵估计存在误差，导致干扰信号子空间估计精度受到限制，从而导致干扰消除性能下降。另一方面，如果增加样本数，由于干扰源运动导致干扰信号的子空间扩散，严重影响算法的干扰消除性能。在低干噪比情况下，由于干扰信号子空间不准确，传统方法的干扰抑制性能不能满足实际工作的需求。为了解决上述问题，本文通过将时变的R_d[n]与多项式模型合并，提出了一种子空间投影波束形成算法的扩展。这种新的基于多项式模型的子空间投影算法(Polynomial-based Subspace Projection, PSP)提高了干扰子空间的跟踪性能。

由于干扰源的移动和天线方向图结构导致从R_{x, k}到R_{x, k+1}的变化是连续的，因此一个适当阶数的多项式拟合可行。假设忽略射电天文信号的影响，这个假设符合常见的射电天文的观测场景，因为射电天文信号的强度过于微弱，以至需要长时间的积分才可以检测到。

时间连续的协方差矩阵R_x(t)，给出了它的采样形式R_x[n]。引入$ {{\mathit{\tilde R}}_\mathit{d}}\left( {t, C} \right) \approx {R_d}\left( \mathit{t} \right)$作为时变的干扰分量R_x(t)的模型，并通过多项式系数矩阵C使其参数化。单干扰信号R_ad(t)=σ_ad²a_d(t)a_ad^H(t)的秩为1，因此可以用r阶的多项式矢量构建时间连续的σ_da_d(t)。

$ \begin{array}{l} \tilde a\left( {t, C} \right) = Ct, \\ t = {\left[{1, t, \cdots ,{t^r}} \right]^H}, \\ {{\mathit{\tilde R}}_\mathit{d}}\left( {t, C} \right) = \tilde a\left( {t, C} \right){{\tilde a}^H}\left( {t, C} \right) = Ct{t^H}{C^H}. \end{array} $

(7)

多项式系数C的估计值可以通过每一个单独短时积分窗的采样协方差矩阵的平方误差最小准则得到。

$ \begin{array}{l} \mathit{\hat C = }{\rm{arg}}\mathit{ }\mathop {\min }\limits_C \sum\limits_{k = 0}^{K - 1} {\left\| {{{\mathit{\tilde R}}_{\mathit{x, y}}} - {{\mathit{\tilde R}}_\mathit{d}}\left( {{t_k}, C} \right)} \right\|_F^2} \\ {t_k} = T\left( {\frac{{2k}}{{K - 1}} - 1} \right) \end{array} $

(8)

其中，t_k为第k个短时积分采样窗口的对应于采样中值标准化的时间值。(8) 式保证了对于0≤k≤K-1，总有-T≤t_k≤T，在多项式拟合窗口中生成了K个短时积分窗。多项式估计的时间尺度标准化是任意的，因为T不代表任何实际的时间或以秒或采样数为刻度的窗口宽度。在估计(6) 式时T作为一个调节参数以限制时间范围，使得高阶的多项式模型不会主导曲线走向，并且在这时多个有界的变化值可以用拟合窗口表示。经过多次仿真分析发现，将T设置为0.75时得到较好的拟合性能。

利用一致性‖A‖_F²=tr{A^HA}将(7) 式代入(8) 式，并且扩展到矩阵形式得到：

$ \begin{array}{l} \mathit{\hat C = }{\rm{arg}}\mathit{ }\mathop {\min }\limits_C \sum\limits_{k = 1}^K {{f_k}}, \\ {f_k} = tr\left\{ {\left. {\hat R_k^H{{\hat R}_k} + C{B_k}{C^H}C{B_k}{C^H} - {{\hat R}_k}C{B_k}{C^H} - C{B_k}{C^H}\hat R_k^H} \right\}} \right., \end{array} $

(9)

其中，B_k=t_kt_k^H。利用(8) 式可以得到解析的梯度和全局最小解以明显减少计算空间，利用数据优化方法改善收敛时间。

有一系列广泛的优化代码可用来解决(9) 式的问题。第4节的仿真结果通过MATLAB的函数fminunc.m得到，它是一种基于内部映射牛顿法的置信域方法。(9) 式的梯度和全局最小解用来确定置信域问题并把这个区域限制在二维子空间。

梯度：虽然多项式的系数是复值，但在平常的优化代码中，它们必须作为独立的实部和虚部计算。在这种情况下，梯度需要改写为

$ \begin{array}{l} {\nabla _\mathit{c}}f = \left[{\begin{array}{*{20}{c}} {{\rm{vec}}\left\{ {\left. {\frac{{\partial \mathit{f}}}{{\partial {\mathop{\rm Re}\nolimits} \left\{ {\left. C \right\}} \right.}}} \right\}} \right.}\\ {{\rm{vec}}\left\{ {\left. {\frac{{\partial \mathit{f}}}{{\partial {\mathop{\rm Im}\nolimits} \left\{ {\left. C \right\}} \right.}}} \right\}} \right.} \end{array}} \right], \\ {\nabla _\mathit{c}}\left( {\sum\limits_{k = 1}^K {{f_k}} } \right) = 4\sum\limits_{k = 1}^K {\left[{\begin{array}{*{20}{c}} {{\rm{vec}}\left\{ {\left. {{\mathop{\rm Re}\nolimits} \left\{ {\left. {\left( {C{B_k}{C^H}-{{\hat R}_k}} \right)C{B_k}} \right\}} \right.} \right\}} \right.}\\ {{\rm{vec}}\left\{ {\left. {{\mathop{\rm Im}\nolimits} \left\{ {\left. {\left( {C{B_k}{C^H}-{{\hat R}_k}} \right)C{B_k}} \right\}} \right.} \right\}} \right.} \end{array}} \right]}, \end{array} $

(10)

全局最小解：用E_st表示一个除了(s, t)位置为1以外全0的初等矩阵，全局最小解可以表示为

$ \begin{array}{l} {H_\mathit{c}}\left( {\sum\limits_{k = 1}^K {{f_k}} } \right) = 4\sum\limits_{k = 1}^K {\left[{\begin{array}{*{20}{c}} {{\rm{vec}}\left\{ {\left. {{\mathop{\rm Re}\nolimits} \left\{ {\left. {{M_1}} \right\}} \right.} \right\}{\rm{vec}}\left\{ {\left. {-{\mathop{\rm Im}\nolimits} \left\{ {\left. {{M_2}} \right\}} \right.} \right\}} \right.} \right.}\\ {{\rm{vec}}\left\{ {\left. {{\mathop{\rm Im}\nolimits} \left\{ {\left. {{M_1}} \right\}} \right.} \right\}{\rm{vec}}\left\{ {\left. {{\mathop{\rm Re}\nolimits} \left\{ {\left. {{M_2}} \right\}} \right.} \right\}} \right.} \right.} \end{array}} \right]}, \\ {M_1} = {E_{st}}{B_k}{C^H}C{B_k} + C{B_k}E_{st}^HC{B_k} + C{B_k}{C^H}{E_{st}}{B_k} - {{\hat R}_k}{E_{st}}{B_k}, \\ {M_2} = {E_{st}}{B_k}{C^H}C{B_k} + C{B_k}E_{st}^HC{B_k} + C{B_k}{C^H}{E_{st}}{B_k} - {{\hat R}_k}{E_{st}}{B_k}. \end{array} $

(11)

此时，(9) 式的直接最优解中包含一个相位模糊，这可能影响数值收敛，因为对任意的角度ϕ，有$ \left( {{e^{j\varphi }}\tilde a\left( {{t_k}, C} \right)} \right){\left( {{e^{j\varphi }}\tilde a\left( {{t_k}, C} \right)} \right)^H} = \tilde a\left( {{t_k}, C} \right){{\tilde a}^H}\left( {{t_k}, C} \right)$。这可以应用到一个任意的时间点t_k上，而其它的所有t_l, l≠k的相位都可以通过多项式的连续性求得。这个模糊可以通过迫使$\angle {\{ \mathit{\hat C}\} _{1, 1}} = 0 $解决，此时有$ \angle {\{ \tilde a(0, \hat C)\} _1} = 0$。文[10]给出的一种参数约束的替代方案是使$\sum\nolimits_{p = 0}^{P - 1} {\angle {{\{ \mathit{\hat C}\} }_{p, 1}} = 0} $，也就是说在元素$\tilde a(0, \hat C) $上有一个0均值相位。这两种方法减少了绝对的相位估计误差方差，但是这两种方法在系统中产生的误差方差也一样，这些值仅仅依赖于相位的不同。这正是$ \tilde a(t, \hat C)$是如何代入(7) 式中以得到${{\tilde R}_d}(t, \hat C) $的，因此由于它在优化代码中更易于实现，选择$ \angle {\{ \mathit{\hat C}\} _{1, 1}} = 0$。

理论上，子空间投影算法可以扩展到处理多个干扰源的情况。此时，$ {{\mathit{\tilde a}}_\mathit{m}}\left( {t, {C_m}} \right)$是m个干扰信号的时变阵列响应。(7) 式改写为

$ {{\tilde R}_d}(t, {\mathit{C}_{\rm{1}}}, \cdots ,{\mathit{C}_\mathit{M}}) = \sum\limits_{m = 1}^M {{C_m}t{t^H}C_m^H.} $

(12)

在数值优化中将梯度和全局最小解扩展到相应的C_m中是一项繁重却很直接的工作。最大的困难在于为每一个C_m找到一个好的初始值。因此，后面的讨论限定干扰维度为1。

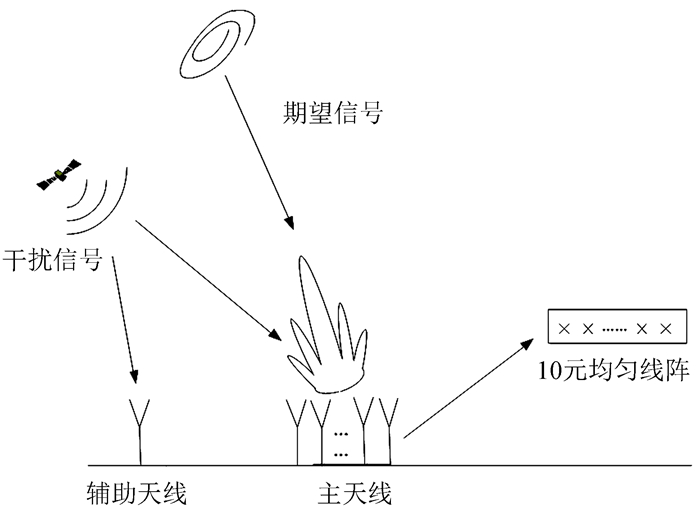
4 仿真和分析

在仿真中尽量保证仿真环境的设置与物理实验平台相符合。详细的数值模型是利用一个10阵元双极化线性半波长宽带的加厚偶极子的相控阵馈源放置在地平面上形成的，其结构如图 3。可用的天线带宽为300 MHz，中心频点为1 600 MHz，同时这也作为仿真生成的窄带信号的中心频率。数据的采样速率为1.25 Msamp/s，带宽为450 kHz。

以调制C/A码的北斗导航信号为干扰信号。短时积分窗序列中的每一个窗口都通过2⁷~2¹⁴个采样点计算，并且所有的短时积分窗使用采样估计校准的噪声协方差矩阵$ {{\mathit{\hat R}}_\eta }$进行预白化。同时每一个相位正确的特征矢量进行多项式拟合。利用(5) 式得到的静态(无干扰)波束形成权矢量$w = \mathit{\hat R}_\eta ^{ - 1}{a_s} $是最大灵敏度的波束，此时有用信号保持在天线的视轴上。

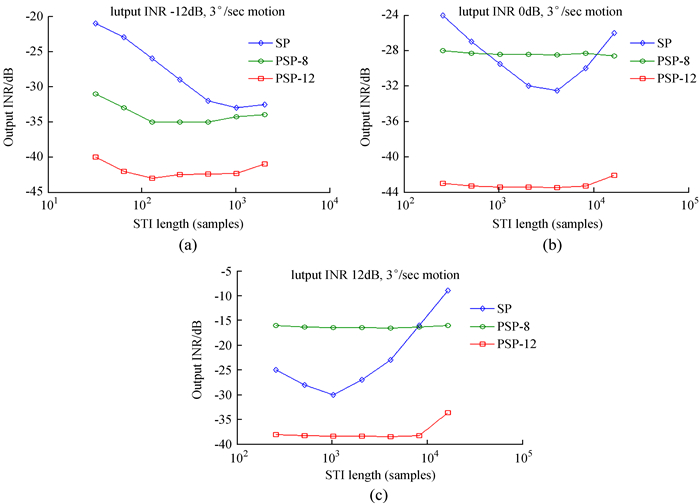
图 4给出了在每一个短时积分窗的协方差矩阵中使用多项式模型拟合与传统的子空间投影算法的性能分析对比。从图中可以看出，子空间投影算法对短时积分的窗口宽度有更高的敏感性，但是子空间投影算法在整个短时积分窗的采样窗口的性能优于子空间投影算法。在很短的短时积分窗采样窗口情况下，子空间投影算法的性能急剧恶化，这是因为此时的采样协方差矩阵有太多的估计误差，不能得到一个良好的特征向量。而子空间投影算法在较短的短时积分窗口宽度的情况下可以得到与较长的短时积分窗口宽度近似的干扰消除性能。图 3和图 1的仿真环境都是在相同干噪比和3°/s的干扰移动速率下进行。在图 3中，PSP-8是指特征矢量是用一个8阶多项式拟合的，PSP-12是指特征矢量是用一个12阶多项式拟合的。

5 结论

本文的研究要点在于：(1) 详细分析了子空间投影算法的性能特点，并研究了限制干扰消除性能的因素，包括采样估计误差和子空间扩散；(2) 提出了一种多项式拟合的方法以更好地构造由干扰移动引起的时变特性。虽然本文是使用射电天文的相控阵馈源仿真和分析算法的有效性，但对于其它的移动干扰环境下的自适应阵列干扰消除有广泛的适用性。

更进一步的工作包括把算法应用到多干扰消除和处理由多径散射带来的秩的增加。本文的实验数据是以秒为单位进行观测的结果，但是实际的射电天文观测中可能需要以小时为单位进行观测。因此，实时处理需要考虑该方法是否可以在实际的天文观测中应用。实时处理的问题包括快速多项式参数估计和波束形成中的自动参数估计问题，因此需要根据不同的数据环境选择不同的多项式阶数。