电子回旋脉泽辐射是捕获在天体磁场中的高能电子直接放大电磁波的一个重要辐射机制。20世纪50年代末，文[1]和文[2]指出，回旋脉泽不稳定性可以在电子回旋频率和谐频率附近直接放大电磁波。随后，文[3]用电子回旋脉泽辐射解释来自木星的十米波辐射，指出回旋脉泽辐射机制在磁化行星中起作用。文[4]在实验室中用相对论电子演示了电子回旋脉泽辐射。后来文[5]指出，具有双麦克斯韦分布的电子在一定条件下可以激发回旋脉泽辐射，但是由于受非相对论共振条件的限制，高能电子具有强温度各向异性分布(T_⊥≫T_‖)(T_‖和T_⊥分别是平行和垂直背景磁场方向的温度)时才能有效激发回旋脉泽不稳定性。1979年，文[6]在解释地球极光千米波辐射时，在共振条件中引进了弱相对论效应，从而定性改变了共振激发的物理图像，大大提高了不稳定性的放大效率，从此电子回旋脉泽辐射作为天体射电辐射的一个重要机制，被广泛应用于解释各种相干射电爆发现象。文[6]提出两个基本假设：(1) 高能电子具有损失锥分布；(2) 关于局域电子密度和磁场强度大小的假设，要求电子等离子体频率远小于回旋频率。

进一步的计算发现，损失锥分布驱动的回旋脉泽生长率仍然过低，因此，根据不同的天体磁等离子体环境，学者们提出了各种电子速度各向异性分布，像环壳(Ring-Shell)^[7]和环束(Ring-Beam)分布^[8]、不完全环壳(Horseshoe)分布^[9]、电子洞(Electronhole)耦合分布等。在磁化等离子体中，电子温度各向异性是一种常见的分布。经典双绝热理论^[10]指出，沿着螺旋磁力线运动的太阳风电子具有大的温度比T_‖/T_⊥，而且这个温度比随着离开太阳的距离增加而增大。然而观测发现，由于动力学不稳定性的触发，在1 AU附近的太阳风电子的温度各向异性是有限的^[11-12]。文[13]研究发现，太阳风电子的温度各向异性与密度有关，在1.5~4之间。对带电粒子和电磁场的实地测量仅限于地球附近的空间，但是可以推测，像太阳日冕、脉冲星、吸积盘等磁化天体等离子体中，同样存在着电子的温度各向异性分布。

在以往的研究中，激发电子回旋脉泽辐射的驱动源是高能电子的各种强各向异性分布。然而，观测显示太阳和其他天体的高能电子常常具有幂律谱能量分布，太阳硬X射线辐射的谱分析显示，耀斑爆发产生的高能电子大都呈现具有低能截止的幂律谱分布^[14-15]，只是具体的截止行为很难由观测分析确定。在最近的研究中，文[16]引入陡化指数参数，通过一个连续的双曲正切函数描述一般形式的幂律谱电子低能截止行为。进一步考虑高能电子在不同磁等离子体环境中形成的速度空间各向异性，完整的分布函数应该是具有低能截止的幂律谱和速度各向异性分布的适当组合，回旋脉泽辐射则是由低能截止行为和速度各向异性共同激发。本文通过计算温度各向异性分布和具有低能截止行为的温度各向异性分布函数对回旋脉泽不稳定性的驱动，研究低能截止行为对温度各向异性驱动的脉泽辐射的影响，结果显示，低能截止存在，即使是弱温度各向异性，也能有效激发回旋脉泽不稳定性的生长率。

1 高能电子分布及生长率表达式

在球坐标系下，考虑双麦克斯韦速度分布^[5]：

$ \mathit{f}\left( \mathit{u}, \mu \right)=\frac{1}{\sqrt{{{\left( 2\pi \right)}^{3}}}\mathit{V}_{\bot }^{2}{{\mathit{V}}_{\parallel }}}\exp \left[-\frac{{{\mathit{u}}^{\rm{2}}}\left( 1-{{\mu }^{2}} \right)}{2\mathit{V}_{\bot }^{2}}-\frac{{{\left( u\mu-U \right)}^{2}}}{2{{\mathit{V}}_{\parallel }}} \right], $

(1)

其中，u=(u_⊥²+ u_‖²)^1/2为单位质量的动量，μ=u_‖/u；V_⊥和V_‖分别为垂直和平行方向上的热速度；U为平行方向的束流速度。

考虑高能电子的幂律谱低能截止分布，结合电子的温度各向异性，高能电子的分布函数为^[17]

$ \mathit{F}\left( \mathit{u}, \mu \right)=\mathit{A}\rm{tanh}{{\left( \mathit{u}/{{\mathit{u}}_{\mathit{c}}} \right)}^{2\delta }}{{\left( \mathit{u}/\mathit{\gamma } \right)}^{-2\alpha -1}}\exp \left[-\frac{{{\mathit{u}}^{\rm{2}}}\left( 1-{{\mu }^{2}} \right)}{2\mathit{V}_{\bot }^{2}}-\frac{{{\left( \mathit{u}\mu-\mathit{U} \right)}^{2}}}{2{{\mathit{V}}_{\parallel }}} \right]. $

(2)

其中，A为归一化系数；双曲正切函数tanh(u/u_c)^2δ描述电子的低能截止行为；δ和α分别为陡化指数和能谱指数；$\mathit{\gamma }=\sqrt{1+{{u}^{2}}/{{c}^{2}}} $为洛伦兹因子。

假设背景热电子的密度比高能电子密度高得多，因此在讨论波的色散关系时可以不考虑高能电子的影响。对于高频电磁波，色散关系可以采用冷等离子体近似^{[8, 18]}：

$ N_{q}^{2}=1-\frac{1}{{{\omega }_{q}}\left( {{\omega }_{q}}+{{\tau }_{q}}\mathit{\Omega } \right)}, $

(3)

其中，

$ {{\tau }_{q}}=-{{s}_{q}}+q\sqrt{s_{q}^{2}+{{\cos }^{2}}\theta }, $

(4)

$ {{s}_{q}}={{\omega }_{q}}\mathit{\Omega }{{\sin }^{2}}\theta /2\left( \omega _{q}^{2}-1 \right), $

(5)

其中，w_q为辐射波的频率，下标q代表波的模式，q=+和q=-分别代表正常模(O模)和反常模(X模)；θ为波矢与磁场方向的夹角；Ω为由等离子体频率归一化的电子回旋频率。

预测波的生长率ω_qi比波的频率ω_q小得多，同时假设背景电子的阻尼可以忽略，那么可以得到波的生长率表达式为^[18]

$ {\omega _{qi}} = - \frac{{{\mathop{\rm Im}\nolimits} \left( {{a_i}\mathit{\boldsymbol{\varepsilon }}_{ij}^ba_j^*} \right)}}{{\frac{\partial }{{\partial \omega }}{\mathop{\rm Re}\nolimits} \left( {{a_i}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}^0a_j^*} \right)}}, $

(6)

其中，ε_ij和Λ_ij分别为介电张量和色散张量；Im(…)和Re(…)代表(…)的虚部和实部；a^*为极化矢量a的复共轭。极化矢量a可以表示为^[18]

$ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over a} = }}\frac{{Kq\hat k + Tq\hat t + i\hat p}}{{{{\left( {K_q^2 + T_q^2 + 1} \right)}^{1/2}}}}, $

(7)

其中，$ \mathit{\boldsymbol{\hat k = }}\frac{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over k} }}{k} = \left( {\sin \theta, 0, \cos \theta } \right)$，$\mathit{\boldsymbol{\hat p = }}\frac{{ - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over k} \times {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over B} }_0}}}{{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over k} \times {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over B} }_0}} \right|}} = \left( {0, 1, 0} \right) $，$ \mathit{\boldsymbol{\hat t = }}\hat p \times \hat k = \left( {\cos \theta, 0, - \sin \theta } \right)$为单位方向矢量。

利用由冷等离子体色散关系$\frac{{\partial N_q^2}}{{\partial k}} = 0 $，对N²-N_q²(ω_q, θ)=0微分，同时对Λ=0微分，则生长率表达式(6) 式可写为^[18]

$ {\omega _{qi}} = - \frac{{{\mathop{\rm Im}\nolimits} {{\left( {{a_i}\mathit{\boldsymbol{\varepsilon }}_{ij}^ba_j^*} \right)}_{\omega = {\omega _q}}}}}{{\frac{\partial }{{\partial N_q^2}}{\mathop{\rm Re}\nolimits} {{\left( {{a_i}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}^0a_j^*} \right)}_{\omega = {\omega _q}}}\left( {\frac{{\partial N_q^2}}{{\partial {\omega _q}}} + \frac{{2N_q^2}}{{{\omega _q}}}} \right)}}, $

(8)

通过计算可以得到：

$ \frac{\partial }{{\partial N_q^2}}{\mathop{\rm Re}\nolimits} {\left( {{a_i}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}^0a_j^*} \right)_{\omega = {\omega _q}}} = {\mathop{\rm Re}\nolimits} \left( {{a_i}\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}^0}}{{\partial N_q^2}}a_j^*} \right) = - \frac{{T_q^2 + 1}}{{K_q^2 + T_q^2 + 1}}, $

(9)

$ \frac{\partial N_{q}^{2}}{\partial {{\omega }_{q}}}+\frac{2N_{q}^{2}}{{{\omega }_{q}}}=\frac{2}{{{\omega }_{q}}}\left\{ \left. 1-\frac{\omega _{q}^{2}\mathit{\Omega }{{\tau }_{\mathit{q}}}}{2{{\omega }_{q}}{{\left( {{\omega }_{q}}+{{\tau }_{\mathit{q}}}\mathit{\Omega } \right)}^{2}}}\left( 1-\frac{q{{s}_{q}}}{\sqrt{s_{q}^{2}+{{\cos }^{2}}\theta }}\frac{\omega _{q}^{2}+\omega _{p}^{2}}{\omega _{q}^{2}-\omega _{p}^{2}} \right) \right\} \right., $

(10)

$ \begin{array}{l} {\mathop{\rm Im}\nolimits} {\left( {{a_i}\mathit{\boldsymbol{\varepsilon }}_{ij}^ba_j^*} \right)_{\omega = {\omega _q}}} = - \frac{1}{{K_q^2 + T_q^2 + 1}}\pi \frac{{{n_b}}}{{{n_0}}}\frac{{\omega _{pb}^2}}{{{\omega ^2}}}\int {{d^3}u{u_ \bot }\left( {1 - {u^2}} \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \left( {\mathit{\gamma } - \frac{{n\mathit{\Omega }}}{\omega } - \frac{{{N_q}u\mu }}{c}\cos \theta } \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times {\left\{ {\left. {\frac{\omega }{\mathit{\Omega }}\left[{\mathit{\gamma }{K_q}\sin \theta + {T_q}\left( {\mathit{\gamma }\cos \theta-\frac{{{N_q}u\mu }}{c}} \right)} \right]\frac{{{J_n}\left( b \right)}}{b} + {{J'}_n}\left( b \right)} \right\}} \right.^2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times \left[{u\frac{\partial }{{\partial u}}\left( {\frac{{{N_q}u\cos \theta }}{{\mathit{\gamma }c}}-\mu } \right)\frac{\partial }{{\partial \mu }}} \right]{F_b}, \end{array} $

(11)

将(9)~(11) 式代入(8) 式可得到波的频率满足$\mathit{\omega }\simeq \mathit{s\Omega }$时，生长率可以表示为^{[8, 16, 18]}：

$ \begin{align} & {{\omega }_{qi}}/{{\omega }_{ce}}=\frac{\pi }{2}\frac{{{n}_{b}}}{{{n}_{0}}}\iiint{{{d}^{2}}\bf{u}\frac{\mathit{\gamma }\left( \rm{1}-{{\mu }^{2}} \right)}{\mathit{\Omega }{{\omega }_{\mathit{q}}}\left( \rm{1}+\mathit{T}_{\mathit{q}}^{\rm{2}} \right){{\mathit{R}}_{\mathit{q}}}}\delta \left( \mathit{\gamma -}\frac{\mathit{s\Omega }}{{{\omega }_{\mathit{q}}}}-\frac{{{\mathit{N}}_{\mathit{q}}}\mathit{u}\mu }{\mathit{c}}\cos \theta \right)} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \times {{\left\{ \left. \frac{\omega }{\mathit{\Omega }}\left[ \mathit{\gamma }{{K}_{q}}\sin \theta +{{T}_{q}}\left( \mathit{\gamma }\cos \theta -\frac{{{N}_{q}}u\mu }{c} \right) \right]\frac{{{J}_{s}}\left( {{b}_{q}} \right)}{{{b}_{q}}}+{{{{J}'}}_{s}}\left( {{b}_{q}} \right) \right\} \right.}^{2}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \times \left[ u\frac{\partial }{\partial u}\left( \frac{{{N}_{q}}u\cos \theta }{c\mathit{\gamma }}-\mu \right)\frac{\partial }{\partial \mu } \right]{{F}_{b}}\left( u-\mu \right), \\ \end{align} $

(12)

其中，

$ \begin{align} & {{\mathit{b}}_{\mathit{q}}}={{N}_{q}}\frac{{{\omega }_{q}}}{\mathit{\Omega }}\frac{u}{c}\sqrt{1-{{\mu }^{2}}}\sin \theta, \\ & {{R}_{q}}=1-\frac{\mathit{\Omega }{{\tau }_{q}}}{2{{\omega }_{q}}{{\left( {{\omega }_{q}}+{{\tau }_{q}}\mathit{\Omega } \right)}^{2}}}\left( 1-\frac{q{{s}_{q}}}{\sqrt{s_{q}^{2}+{{\cos }^{2}}\theta }}\frac{\omega _{q}^{2}+1}{\omega _{q}^{2}-1} \right), \\ & {{K}_{q}}\frac{\mathit{\Omega }\sin \theta }{\left( \omega _{q}^{2}-1 \right)\left( {{\omega }_{q}}+{{\tau }_{q}}\mathit{\Omega } \right)}, {{T}_{q}}=\frac{\cos \theta }{{{\tau }_{q}}}, \\ \end{align} $

(13)

上述(12) 式中n₀和n_b分别为背景等离子体电子数密度和高能电子数密度；ω_ce为电子回旋频率；J_s(b_q)和J′_s(b_q)为第一类贝塞尔函数和它的导数。

2 生长率计算结果

在弱相对论近似及冷等离子体假设下，把高能电子分布函数(1) 式和(2) 式代入(12) 式，可以得到波的生长率。

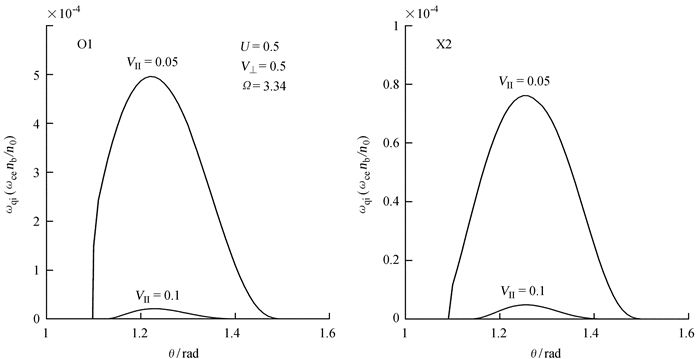
图 1是温度各向异性(双麦克斯韦分布)驱动的回旋脉泽辐射峰值生长率与传播角的关系，O1和X2分别代表正常模基波和反常模谐波。高能电子的参数和背景等离子体参数如图中所示，所有的速度都用光速归一化，频率用等离子体频率归一化，生长率由ω_cen_b/n₀归一化。

从图 1可以看出，温度各向异性可以激发回旋脉泽不稳定性，而且各向异性分布越强，不稳定性的生长率越高。当温度各向异性降低，比如V_⊥=0.5，V_‖=0.2时，不稳定性的生长率为0 (图中没有画出)，也就是说只有在温度各向异性较强时，才能激发回旋脉泽辐射。另外计算表明，双麦克斯韦分布函数(1) 式只有在V_⊥ > V_‖时才能驱动不稳定性生长。

图 2和图 3是分布函数(2) 式驱动的回旋脉泽生长率与传播角的关系。高能电子和背景等离子体参数如图中所示，图 2中不同曲线代表不同的陡化指数δ，图 3中不同的曲线代表不同的垂直方向热速度V_⊥。结果显示，即使是原来不能激发回旋脉泽辐射的弱各向异性(V_⊥=0.5，V_‖=0.2)，只要低能截止存在就可以激发回旋脉泽不稳定性，而且生长率随着陡化指数的增加而增大。图 3结果表明，即使在V_⊥ < V_‖条件下，低能截止仍然可以有效激发回旋脉泽辐射。图 2和图 3还显示，低能截止使不稳定性的角范围大大增宽，最大生长率的传播角也更加趋近于垂直方向。

3 结论

电子回旋脉泽辐射是天体射电辐射的一种重要机制，被广泛应用于解释各种短时标、高亮温度的相干射电爆发现象。在以往的研究中，一个重要的假设就是激发回旋脉泽辐射的高能电子具有强各向异性速度分布。而观测显示高能电子常常呈幂律谱分布，计算了纯温度各向异性分布和具有低能截止行为的温度各向异性分布对回旋脉泽不稳定的激发。研究表明，纯温度各向异性可以激发回旋脉泽辐射，但是要求具有较强的各向异性。而当高能电子存在低能截止行为时，即使是不能激发回旋脉泽不稳定性的弱温度各向异性(V_⊥=0.5，V_‖=0.2) 或在V_⊥ < V_‖条件下，也可以有效激发脉泽不稳定性，而且不稳定性的角范围大大增加。