2. 中国科学物理研究所, 北京 100190
2. Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
受卫星星座几何分布图形的影响,卫星导航系统在高程方向上的定位精度一般较差。其单频粗码定位误差一般为几米至十几米,在信号遮挡或定位条件较差时甚至达几十米。并且,作为同一组最小二乘估计解,高程解算值与其他未知数之间是相关的,高程坐标的误差也会影响用户二维平面坐标及接收机钟差的解算精度。因此,高程定位精度欠佳一直是卫星导航系统存在的一大问题。
针对这一问题,学者们进行了大量的研究,希望能够通过其他方法或手段获得比直接定位解算更精确的高程值,以改善高程定位误差较大的问题。同时,这样也能够对测量方程组形成高程约束条件,从而提高二维平面及接收机钟差的解算精度。在我国北斗一代卫星定位系统及文[1-3]中,曾采用数字高程模型 (Digital Elevation Model, DEM) 与电子地图获得用户大地高。而在中国区域卫星定位系统 (China Area Positioning System, CAPS)[4-6]I期中,也曾利用气压测高技术辅助当时尚不完善的卫星星座实现三维定位[7]。文[8-9]提出进一步将气压测高技术应用于地面移动通信基站中,将其作为气压校正基准点并利用通信传输链路将相关测量数据传送给附近用户,以修正获得高精度的用户绝对高程值。文[10]根据高程坐标分量与接收机钟差之间存在高相关性的特征,在差分站的基础上模拟和预测接收机钟差,并在定位方程组中添加一个关于接收机钟差变化的辅助方程,以减小垂直精度因子值,提高高程定位精度[10-11]。
以上方法虽然能在不同程度上改善高程误差,提高定位精度,但都需要增加额外设施或手段,在增加投入与成本的同时,也加大了定位系统的复杂性。为此,本文提出一种利用卫星导航系统自身定位信息有效提高高程定位精度的方法。通过引入高程方向速度测量值、结合高程定位值,设计组成一个一定长度的滤波器,不断利用最新测量值对用户高程进行实时平滑处理。由于即使当高程方向上的定位误差较大时,高程方向上的速度值也能够具有很高的精度,因此滤波器能够有效获得高精度的用户实时定位高程值,且无需增加任何额外设备。该方法既能用于正常定位,有效提高定位精度,也能用于卫星信号短暂缺失的非完备定位情况,帮助实现三维定位。另外,由于卫星定位星座分布的原因,其高程坐标分量与接收机钟差之间存在着很高的相关性[11]。因此在高程精度得到提高的同时,其接收机钟差解算精度也能相应提高。最后,通过全球定位系统实测实验对方法进行了分析与验证。实验结果表明,该方法效果显著,简单易行,具有很强的实用性。
2 速度平滑高程原理与方法在车载、船舶定位等应用领域,用户运动状态符合牛顿惯性运动定律,其高程位置的变化一般较为缓慢和平滑。因此,将每个历元的定位过程独立起来、以单点定位解算结果得到的高程值作为最终的输出结果,显然不是最佳选择。实际上,由于即使当高程坐标分量的定位误差较大时,高程速度分量也能够具有很高的精度,因此完全可以将两者结合起来,利用高程解算值获得绝对起始值,利用速度解算值获得准确的高程变化量,从而构成一个组合滤波器,对高程值进行平滑。
这种思想与卫星导航中载波相位平滑伪距测量值的方法[12-13]类似,都是通过对精度欠佳的绝对测量值取均值的方式获得一个较为准确的绝对起始值,并利用高精度的相对测量值获得该绝对起始值的变化量。
2.1 速度平滑高程滤波器设计对于用户在最新历元n的高程值,可利用之前l个高程解算值Hn-i(i=1, 2, …, l) 获得其l个高程估计值

|
(1) |
其中,vn-kH(k=1, 2, …, l) 为高程方向的速度分量;k代表参与平滑的历元数;T为定位时间间隔。可根据这一系列估计值以获得最新历元n的高程平滑值Hn:

|
(2) |
若考虑当前历元n时,用户实际定位解算结果Hn,则可利用上述方法先求得Hn-1,并按加权均值方式获得平滑后的高程值:

|
(3) |
(3) 式即为一般的速度平滑高程滤波器,l为滤波器的长度,l值越大,Hn越依赖于速度值,Hn也就越平滑。
对于何时开启滤波器分为两种情况:一是等待定位历元数达到滤波器长度l,由此获得准确的平滑值Hn-1,再根据 (3) 式开始正常运行滤波器;二是从定位过程一开始即开启滤波器,采用正常定位后的第1个高程解算值H1初始化Hn的值:

|
(4) |
并根据历元数的增加,不断更新Hn的值,直至达到滤波器长度l为止。第2种方式能够使滤波器从定位一开始即得到运用,但由于定位初期历元数较少,因此可能会受较大误差值的影响而在初期产生一定的偏差,滤波器需要经过一段时间的运行并达到理想设计长度后,才能逐渐趋于稳定并消除此偏差。
2.2 滤波器精度分析由 (1) 式至 (3) 式可以看出,速度平滑高程滤波器的误差主要来自两方面:一是各历元实际高程解算值经平均后剩下的误差;二是各历元速度解算值在滤波器长度l内的累积误差。
由 (1) 式可得

|
(5) |
设每次定位的高程坐标分量均方误差为σH,高程速度分量均方误差为σv,根据误差传播律可得Hn的均方误差σH[14]:

|
(6) |
目前全球导航卫星系统的高程速度误差σv一般小于0.3 m/s,而接收机定位间隔T约为0.1~1 s。因此,(6) 式右端由速度误差造成的影响很小。故可近似认为滤波器精度为

|
(7) |
通过一个长度为l的速度平滑高程滤波器,能够将高程坐标分量均方误差减小至原来的约1/l。
3 速度平滑高程定位方法 3.1 正常星座情况下的增强定位方法当可视卫星多于4颗时,同时存在两类定位算法:后台不断利用正常定位解算得到的高程值Hn,通过滤波器得到用户实时高程平滑值Hn;而增强算法则将Hn作为已知量处理,重新对测量方程组进行求解。方法流程如图 1。

|
| 图 1 增强算法流程图 Figure 1 Enhancement algorithm flowchart |
此时,增强算法实际上相当于减少了一个未知数,对原测量方程形成高程约束条件:

|
(8) |
其中,n≥4为观测卫星个数;xi、yi和zi为第i颗卫星在地心地固坐标系下的坐标;ρi为第i颗卫星至用户的伪距观测值;x、y、z和Δt是待求量,分别为用户接收机位置坐标及接收机钟差;a、b为地球基准椭球的长、短半轴;h为用户海拔高Hn经简单坐标转换后的大地高。关于 (8) 式的具体解算方法可见文[15-18]。
3.2 非完备情况下的辅助定位方法当可视卫星少于4颗时,称为非完备星座情况。若不依赖其他辅助手段或信息,用户将无法完成正常定位。此时,可利用之前稍早的高程定位值进行外推,以获得非完备情况下的高程预测值,从而将定位解算问题变为二维。
相比于直接对高程定位值进行建模和外推,利用根据滤波器进行平滑后的高程值序列进行外推的主要优势在于:(1) 经过滤波器平滑后的高程值更为准确,因此对其进行建模和预测也能够获得更高的精度;(2) 由于平滑后得到的高程序列曲线更为明显,因此在对其进行拟合和外推时能够采用更少的先验数据,减小计算量;(3) 由于各个历元的高程值经过了足够长度窗口的平滑,所以可以有效避免和克服观测数据突变带来的粗差,抗差性显著提高。
另外需要指出,预测高程辅助非完备定位的效果很大程度上取决于用户所处的运动环境。若用户位于较平坦的地区,高程变化较为缓慢,则预测高程可以在很长一段时间内辅助非完备定位。甚至可以采用对先验高程值序列进行均值或加权均值的处理方法,即能获得良好的定位效果。相反,若用户高程变化较为剧烈,预测高程将难以反映真实高程的变化情况,从而使方法效果受限。
4 实验与分析利用中科微电子有限公司研制的CASIC卫星导航接收机模块,以1 Hz频率通过串口传输方式输出自定义二进制格式的全球定位系统卫星广播星历及单频、C/A码伪距测量数据。基于该模块及输出编程,并进行实时定位实验与验证。
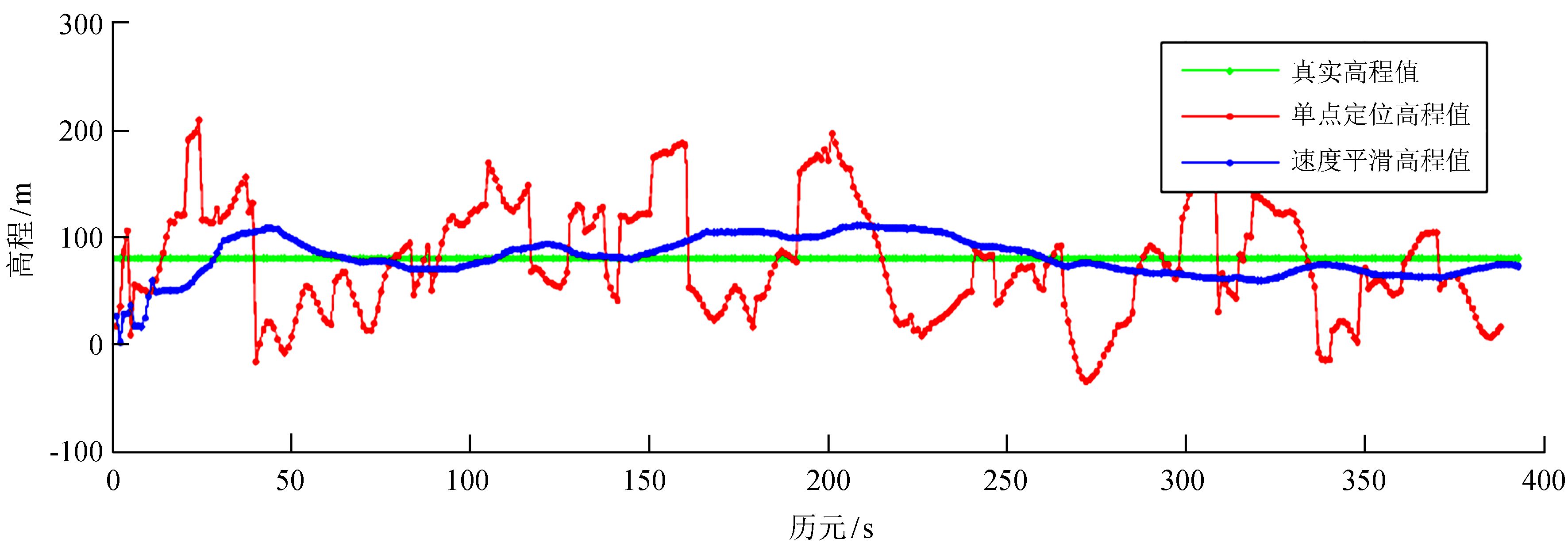
为更明显地分析和比较滤波器及定位方法在正常星座情况时的性能,在某个具有一定遮挡的已知坐标点上进行长时间的静止测量。首先,直接解算得到用户在该点上全部观测历元的高程坐标值;然后,采用一个长度为100 s的速度平滑高程滤波器对其进行平滑处理,两者结果如图 2。
|
| 图 2 高程坐标分量对比 Figure 2 Precision comparison of elevations |
可以看出,经速度平滑后得到的高程更加平滑、稳定,与真实高程值更为吻合。在此基础上按图 1流程进行增强定位方法解算,并与原定位结果比较,结果如图 3。

|
| 图 3 增强算法定位解算结果对比。(a) 二维定位结果对比;(b) 接收机钟差解算结果对比 Figure 3 The positioning results of enhanced algorithm and original method. (a) Comparison for 2D positioning results; (b) Comparison for the clock error of the GPS receiver |
统计图 3(a)中的误差可知,增强算法将原始二维定位误差减小了约30%,具有显著的效果;而图 3(b)中的接收机钟差值序列也更为平滑,符合实际规律,说明由于高程坐标分量与接收机钟差之间的高相关性,更准确的高程确实能够带来更准确的接收机钟差值,从而能够帮助提高接收机的授时精度。
5 结论受星座分布几何图形的影响与制约,高程定位精度一直是全球导航卫星系统的一大短板。为此,曾提出使用电子地图匹配、气压测高、基准站差分修正等多种手段以获得更准确的高程值,从而提高全球导航卫星系统高程及三维定位精度。然而,这些方法通常需在用户或定位基准端配备额外的硬件设施,在加大成本的同时也增加了系统的复杂性。并且,由于电子地图及气压测高技术一般只能将用户高程定位精度提高至1 m左右,因此仅能应用于单频、粗码等一般民用领域。而当采用差分、多频或载波相位等高精度定位手段后,全球导航卫星系统高程定位精度本身已优于1 m,此时上述方法将难以继续起到提升作用。
实际上,类似于载波相位平滑伪距的方法,卫星定位中高精度的相对测量值总是能够对绝对测量值进行修正,提高其测量精度。基于这一思想,本文提出结合使用高程坐标分量与速度分量,利用高精度的速度解算值对高程定位值进行平滑与修正。由此设计的组合滤波器简单规范,易于实现,且无需增加任何额外设备。通过一段不长时间的平滑过程,既能获得高精度的高程坐标,具有很强的工程实用性。并且,由于当高程分量精度提高时,其速度分量亦能具有相对更高的精度,因此方法能够适用于各种精度需求的应用领域。
实测实验与分析证明,该方法能够显著提高全球导航卫星系统高程及三维定位精度。同时,由于滤波器处理后的高程值序列具有很高的精度与良好的曲线平滑性,因此适于拟合与外推,从而辅助卫星信号缺失的非完备情况实现三维定位。由于卫星定位高程坐标分量与接收机钟差之间存在很高的相关性,在高程精度得到提高的同时,接收机钟差解算精度也能相应提高,从而获得更高的授时精度。因此,该方法能够在多方面对全球导航卫星系统进行增强与辅助,具有良好的实用效果和应用价值。
| [1] | Ptasinski P, Cecelja F, Balachandran W. Altitude aiding for GPS systems using elevation map datasets[J]. Journal of Navigation , 2002 , 55 (3) : 451 –462. |
| [2] | French R L. Map matching origins, approaches and applications[C]//Proceedings of the Land Vehicle Navigation. 1989: 91-116. |
| [3] | Zavoli W B, Honey S K. Map matching augmented dead reckoning[C]//Vehicular Technology Conference. 1986: 359-362. |
| [4] |
艾国祥, 施浒立, 吴海涛, 等. 基于通信卫星的定位系统原理[J]. 中国科学G辑:物理学力学天文学
, 2008 , 38 (12) : 1615 –1633 |
| [5] | Ai Guoxiang, Shi Huli, Wu Haitao, et al. The principle of the positioning system based on communication satellites[J]. Science in China Series G: Physics, Mechanics and Astronomy , 2009 , 52 (3) : 472 –488. DOI: 10.1007/s11433-009-0065-6 |
| [6] | Ai Guoxiang, Shi Huli, Wu Haitao, et al. A positioning system based on communication satellites and the Chinese Area Positioning System (CAPS)[J]. Chinese Journal of Astronomy and Astrophysics , 2008 , 8 (6) : 611 –630. DOI: 10.1088/1009-9271/8/6/01 |
| [7] | Ai Guoxiang, Sheng Peixuan, Du Jinlin, et al. Barometric altimetry system as virtual constellation applied in CAPS[J]. Science in China Series G: Physics, Mechanics and Astronomy , 2009 , 52 (3) : 376 –383. DOI: 10.1007/s11433-009-0060-y |
| [8] | 张丽荣, 施浒立, 邓中亮, 等. 基于基准站的气压相对测量求得精确高程的方法: 中国, 201110082773. 5[P]. [2016-05-20]. |
| [9] |
杜晓辉, 裴军, 张丽荣, 等. 基于地面移动通信基站的差分气压测高方法[J]. 北京航空航天大学学报
, 2013 , 39 (1) : 83 –88 Du Xiaohui, Pei Jun, Zhang Lirong, et al. Differential barometric altimetry method based on mobile phone base stations[J]. Journal of Beijing University of Aeronautics and Astronautics , 2013 , 39 (1) : 83 –88. |
| [10] | Misra P, Pratt M, Burke B, et al. Adaptive modeling of receiver clock for meter-level DGPS vertical positioning[C]//Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation. 1995: 1127-1135. |
| [11] |
谢钢. GPS原理与接收机设计[M].
北京: 电子工业出版社. 2009.
|
| [12] | Hatch R. The synergism of GPS code and carrier measurements[C]//Proceedings of the Third International Geodetic Symposium on Satellite Doppler Positioning. 1982. |
| [13] | Misra P, Enge P. Global Positioning System-signals, measurements, and performance[M]. Lincoln, MA: Ganga-Jamuna Press. 2001. |
| [14] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M].
武汉: 武汉大学出版社. 2003.
|
| [15] |
孔祥元, 郭际明, 刘宗泉, 等. 大地测量学基础[M].
武汉: 武汉大学出版社. 2010.
|
| [16] |
乔仰文, 辛久志, 王晓辉, 等. GPS高程转换的若干问题的研究[J]. 测绘通报
, 1999 (11) : 17 –19 Qiao Yangwen, Xin Jiuzhi, Wang Xiaohui, et al. A study on some problems of GPS height transformation[J]. Bulletin of Surveying and Mapping , 1999 (11) : 17 –19. |
| [17] |
施浒立, 孙希延, 李志刚. 转发式卫星导航原理[M].
北京: 科学出版社. 2009.
|
| [18] | Shi Huli, Pei Jun. The solutions of navigation observation equations for CAPS[J]. Science in China Series G: Physics, Mechanics and Astronomy , 2009 , 52 (3) : 434 –444. DOI: 10.1007/s11433-009-0049-6 |


